Об управлении H-процессами
Автор: Медведев А.В.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 3 т.17, 2016 года.
Бесплатный доступ
Исследуется проблема управления дискретно-непрерывными процессами, которые имеют «трубчатую» структуру в пространстве входных-выходных переменных. Подобные процессы протекают в пространствах дробной размерности. Моделирование и управление процессами этого класса существенно отличаются от общепринятых параметрических моделей, представляющих собой поверхности в том же пространстве. При построении обучающихся параметрических моделей «трубчатых» процессов необходимо использование соответствующих непараметрических индикаторов. Многомерный Н-процесс включает в себя как управляемые, так и неуправляемые векторные переменные, при этом неуправляемые входные переменные контроли- руются в процессе функционирования многомерной системы. Естественно задающие воздействия также представляют собой вектор. При управлении Н-процессами необходимо компоненты вектора задающих воздействий согласовывать между собой, а не задавать их произвольно, как это принято в теории автоматического управления. В результате возникает необходимость синтеза -регулятора, а не -регулятора. На первом этапе необходимо выделить некоторую область пересечения всех Н-процессов по каждой компоненте выходной переменной, для этого используется соответствующий индикатор. В результате получаем некоторую подобласть согласования в пространстве входных-выходных переменных. Только из этой подобласти можно определить задающее воздействие для каждой компоненты выхода многомерной системы. Следующий этап - это вычисление управляющих воздействий при фиксированном значении векторов входных неконтролируемых переменных. Анализируется случай, когда задающие воздействия для компонент выходных переменных не удается в конкретной ситуации согласовать или согласовать частично. Приводятся алгоритмы определения компонент вектора задающих воздействий. Даны также непараметрические алгоритмы управления многомерными Н-процессами. В результате такое управляющие устройство можно отнести к матричным системам управления. Таким образом, последний реализует как алгоритм определения задающих воздействий, так и алгоритм управления объектом. Он-то и является -регулятором (управляющей системой) для многомерного Н-процесса. Естественно, могут возникать случаи, когда Н-процессы по всем компонентам выхода оказываются непересекающимися. В подобной ситуации необходим поиск приемлемых компромиссов с целью поэтапного приведения состояния управляемого процесса к желаемому.
Н-процесс, h-модели, безынерционный объект, пространство дробной размерности, индикатор, подпространство согласования, -регулятор
Короткий адрес: https://sciup.org/148177599
IDR: 148177599 | УДК: 539.3
Текст научной статьи Об управлении H-процессами
Введение. Идентификация многих стохастических объектов часто сводится к идентификации статических систем с запаздыванием. Обусловлено это тем, что некоторые выходные переменные объекта контролируются через значительно большие интервалы времени, чем входные, и существенно превышают постоянную времени объекта. Например, ряд переменных измеряется электрическим способом (в этом случае дискретность контроля A t может быть достаточно мала), а другие переменные контролируются в результате химического анализа или физико-механических испытаний (в этом случае дискретность контроля A T велика, т. е. A T >> A t ). В результате, переходный процесс, протекающий в объекте, устанавливается за значительное меньшее время, чем измерение выходной переменной.
Идентификация статической системы. Пусть и = ( иъ ...,uk ) ей ( и ) ■ Rk , ц = ( ц , , ..., ц „ ) ей ( ц ) с R" , а x = ( x 1 , ..., x m ) ей ( x ) с R m . Вообще говоря, каждая компонента вектора u i е [ a i ; b i ], i = 1, к , Ц у е [ C j ; d j ], j = 1, n , а x q е [f q ;e q ], q = 1, m . При исследовании реальных процессов значения коэффициентов { a i ,b i ,C j , d j , fq , e q } , i = 1, к , j = 1, n , q = 1, m , всегда известны. В технологических процессах значения этих коэффициентов регламентируются технологическим регламентом (картой). В дальнейшем, без нарушения общности, эти интервалы примем единичными [1], тогда й ( и ) - единичный гиперкуб, й к ( и ) = [0;1], й n ( ц ) = [0;1], т. е. и е [0;1], ц е [0;1], й к + n + m ( и , ц, x ) = [0;1], ( и , ц, x ) е й к + n + m ( и , ц, x ).
Задачу идентификации часто сводят к параметрической, состоящей из двух основных этапов. Первый этап - выбор (определение) параметрической модели в виде x ( и , ц ) = f ( и, ц, а ), где а - вектор параметров, и на втором этапе - последующая оценка параметров а на основании поступающих элементов выборки ( и 1, Ц 1 , x 1),( и 2 , ц 2 , x 2 ), —,( U s , Ц s , X s ), т. е. получение оценки а s . Адаптивная модель в этом случае будет выглядеть следующим образом:
x ( и , ц ) = f ( и, ц, а ). (1)
Оценка параметров а при наличии обучающей выборки может быть осуществлена методом наименьших квадратов или методом стохастических аппроксимаций. Такова общая схема решения задач параметрической идентификации. Отметим только, что наиболее слабым местом здесь является выбор параметрической структуры модели. Если на первом этапе допущена достаточно грубая ошибка, то, в итоге, полученная модель вряд ли будет удовлетворительной. Эта проблема достаточно подробно обсуждалась в [2; 3]. Там же предложен новый класс K -моделей, учитывающий в комплексе знание фундаментальных законов, другую априорную информацию об объекте, в том числе разнотипную. Обратим внимание на то, что модели класса (1) представляют собой гиперповерхности в пространстве входных-выходных переменных объекта, т. е. ( и , ц , x ) ей ( и , ц , x ) с R ^ + " + m . Процессы трубчатой структуры, или Н -процессы [4], представлены на рис. 1. Поскольку значение входных неуправляемых переменных влияет на расположение реального Н -процесса при отличающихся ц , то это обстоятельство отражено на рис. 1. На рис. 1, а представлен Н -процесс при ц = ц ’ , на рис. 1, б - при ц = ц" .
Если исследуемый процесс имеет «трубчатую» структуру, то модель (1) необходимо подкорректировать следующим образом [2]:
x s ( и , ц ) = I s ( и , ц ) f ( и , ц , а s ) (2)
либо:
N x s ( и , ц ) = I s ( и , ц ) Е а Л ( и , ц ), (3)
j = 1
где ф j ( и , ц ) - система линейно независимых функций; индикатор Is ( и , ц ) имеет вид
I s ( и , ц )
1,
0,
если и е й H ( и ), ц е й H ( ц ); если и е й H ( и ), ц е й H ( ц ).
Заметим лишь, что, вообще говоря, область й H ( и , ц ) нам не известна, а известна лишь выборка { x i , u i , ц i , i = 1, s } . Это обстоятельство особенно хорошо видно при анализе рис 1.
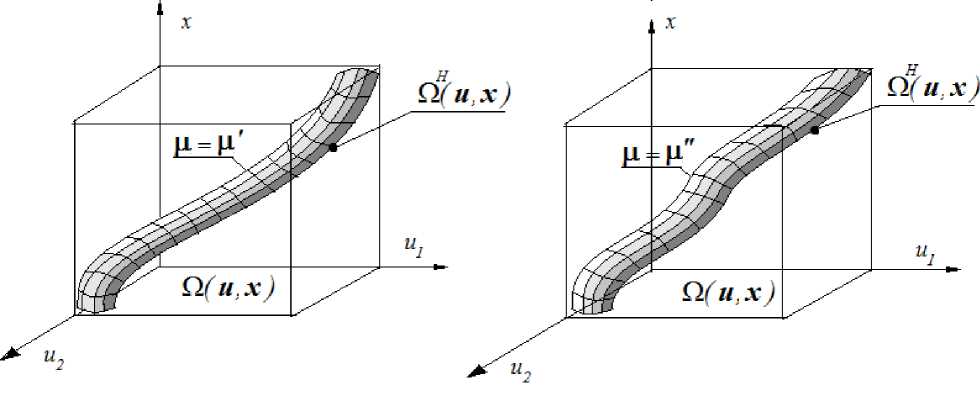
Рис. 1. Трубчатый процесс
Если индикатор равен нулю, то оценка x ( и , ц ), x s ( и , ц ) не может быть вычислена, т. е. при таких значениях компонент вектора и е Q ( и ), ц е О ( ц ) процесс протекать не может. Если индикатор I s ( и , ц ) при любом значении и е Q ( и ), ц е О ( ц ) равен единице, то модель (2) совпадает с (1). В качестве оценки индикатора I s ( и , ц ) можно принять следующее приближение:
Is (u) = sgn(scs )-1 £ Ф(с-1 (Xs (и) - Xi ))х i=1 km хП ф(<*(и - и/ ))П ф(<*(н1 -ц 1)),(5)
j =1
где skm xs(и) = Z xi П Ф(с-1 (uj - и/ ))П Ф(с-1 (ц1 - ц1)) / i=1 j=1
skm
/ Z П ф(с;1 (иj - и/ ))П ф(с-1 (ц1 - ц 1)),( i=1 /=1
а параметр размытости cs и колоколообразная функция Ф( - ) удовлетворяют условиям сходимости [5; 6]. Подобные непараметрические оценки достаточно подробно исследовались в [7; 8].
Таким образом, при известных значениях и = и ' е Q ( и ), ц = ц ' е О ( ц ) сначала строится оценка x s ( и = и ', ц = ц ‘ ) по формуле (6), затем вычисляется индикатор I s ( и ), и только на следующем этапе используются модели (2) или (3), если индикатор оказался равным единице. Если же индикатор равен нулю, то это означает, что хотя и' е Q ( и ), ц ‘ е О ( ц ), но и' е Q H ( и ), ц ’ е Q H ( ц ), т. е. компоненты вектора и = и' = ( и ’ , ..., и к ), ц = ц '= ( ц ‘ , ..., ц к ) определены неверно, иными словами, реально протекающий «трубчатый» процесс не соответствует совокупности
заданных значений компоненты векторов и = и' , ц = ц ’ . Причины этого могут состоять в том, что компоненты векторов и = и ' = ( и ’ , ..., и'к ), ц = ц ' = ( ц ‘ , ..., ц к ) выбраны неверно либо измерены с значительной погрешностью типа «выброс». Конечно же, это справедливо только при условии, что мы располагаем представительной выборкой { x i , ui , ц i , i = 1, s } . Следует заметить, что использование традиционных моделей типа (1) позволит получить оценку x ( u = и ', ц = ц ‘ ), которая, естественно, будет далека от реальности.
Естественно считать, что процесс идентификации объекта в параметрической постановке также следует осуществлять с учетом «трубчатой» структуры объекта. Примем модель «трубчатого» процесса в виде (из соображений простоты ц отпущено)
N
х ( и ) = I ( и ) £ а / Ф / ( и ), (7)
/ = 1
где ф / ( и ), j = 1, N - система выбранных линейно независимых функций; I s ( и ) - индикаторная функция (5).
Сформируем критерий оптимальности:
I N
R(а) = M Яx(и) - I(и)ZаjФ/(и))2 ’
I j = 1
Наша цель состоит в отыскании таких а* = ( а* , ••■, a*N ), что
R ( а * ) = min R ( а ).
а
Решение задачи (9) дается системой рекуррентных соотношений:
а s =а s-1 +Y s
xs - Is ( Us )Zа s-1Ф j ( Us )
X Ф / ( Us ) I s ( Us ) , l = 1, ..., N .
X
В качестве оценки I ( us ) примем приближения: sk j
I s ( U s ) = Sgn( SC s ) - 1 £П Ф (11) i = 1 j = 1 ( c s J
Ясно, что сходимость a s к a * следует при s ^« . Учет неуправляемых, но контролируемых входных переменных μ в приведенном выше примере, не вызывает затруднений.
Об одной особенности моделирования «трубчатых» процессов. Приведем следующий пример, имеющий отношение к идентификации безынерционной системы. Рассмотрим следующий простой частный случай. Пусть объект описывается уравнением:
X(u) = f (U1,u2,u3), (12) где трехмерный вектор u = (u1, u2, u3) e R3 является входной переменной, а x e R1 - выходная переменная. Традиционный путь построения модели процесса, описываемого (12), состоит в определении класса параметрических зависимостей x(u) = /(u1,u2,u3,a) и последующей оценки параметров a тем или иным способом по выборке наблюдений (ui, xi), i = 1, s, где s – объем выборки. Проанализируем этот пример с разных точек зрения. Пусть компоненты вектора входных переменных u = (u1, u2, u3) стохастически никак не связаны, т. е. независимы. В этом случае естественно использовать обычный традиционный прием, описанный выше. Теперь предположим, что объективно компоненты вектора входных переменных функционально связаны, например, u2 = Ф1(u1), u3 =Ф2(u2) = Ф2<Ф1(«1))- (13)
Такая ситуация рассматривалась в [9]. Естественно, исследователь не знает о существовании зависимостей (13). В противном случае можно было бы сделать подстановку (13) в (12) и получить следующую зависимость x уже от одной переменной u 1 вида
x(u) = f(u1, Ф1(u1), Ф2 (Ф1(u1))). (14)
Таким образом, зависимость (12) в приведенных выше условиях может быть сведена к одномерной зависимости x от u 1 . В случае, если зависимость u 3 от u 2 объективно отсутствует, то (12) легко приводится к виду
X (u) = f (u1, Ф1( u1), u 3), (15) т. е. к двумерной зависимости x от u1 , u3 . Отсюда можно заключить, что при наличии функциональной зависимости между компонентами вектора u мы получаем зависимость x от u , в данном случае одно-, двух-, трехмерные. Подчеркнем еще раз, что о наличии функциональных зависимостей между компонентами вектора входных переменных исследователю не известно. Просто мы проанализировали случай «если бы…». А теперь проанализируем наиболее интересный случай, имеющий непосредственное отношение к H-процессам [1]. Пусть u3 и u2 , хотя и неиз- вестным образом, но стохастически связаны. Подчеркнем – стохастически, а не функционально. Вернемся еще раз к анализу того, что произошло. Во-первых, если компоненты вектора u независимы, то исследуемый процесс описывается функцией трех переменных. Если две компоненты вектора входных переменных u связаны функциональной зависимостью, то процесс описывается функцией двух переменных. Наконец, если две переменные связаны стохастически, то процесс описывается функцией более чем двух переменных, но менее чем трех?! Можно считать, что мы приходим к зависимости от дробного числа переменных и, следовательно, к пространству дробной размерности. Например, Б. Мондельброт в [10] замечает: «Кровеносная система человека – пульсирующая, живая – имеет размерность 2.7». Дробная размерность пространств, по видимому, впервые была отмечена в работах Хаусдорфа и Бези-ковича.
Рассмотрим следующую ситуацию. Из простоты соображений, пусть интересующий нас процесс описывается (12).
В случае стохастической зависимости между переменными u 2 ( u 1 ), u 3 ( u 1 ) по имеющимся в наличии обучающим выборкам можно вычислить квадратичную ошибку прогноза u 2 s ( u 1 ), u 3 s ( u 1 ). Здесь u 2 s ( u 1 ), u 3 s ( u 1 ) есть непараметрические оценки (6) [3]:
^ 21 = ^ ( u 2 - u 2 s ( u 1 ) ) M 3 u 2 , i =1 /
8 31 = E ( u 3 - u 3 s ( u 1 ) ) 2 /3 2 3 . (16) i =1 /
«Силу» стохастической связи X между двумя произвольными переменными можно, например, вычислить по формуле:
X = 1 -8 , (17) где 8 может быть равно 8 21 либо 8 31.
Отсюда видно, что самая сильная стохастическая связь (функциональная) равна 1, отсутствие связи – при X = 0, а при стохастической зависимости между входными переменными 0 < X < 1. Последнее легко прослеживается из следующих рассуждений: если переменные u 1 , u 2 , u 3 независимы, то (12) не более чем функция 3-х переменных. Если u 1 , u 2 связаны функционально, то в результате подстановки в (12) мы приходим к функции 2-х переменных. Если функционально связаны все переменные u 1 , u 2 , u 3 , то в результате подстановки приходим к функции 1-й переменной. Наконец, если u 1 , u 2 , u 3 связаны стохастически, то размерность пространства естественно уменьшается и может лежать в интервале от 2 до 3 либо от 2 до 4. Это зависит от тесноты связи, т. е., например, от значения X .
Если в более общем случае такого рода процессы интерпретировать как функции многих переменных, то изменчивость этой функции во времени может быть, например, показана на нижеследующей цепочке соотношений, действующих во времени:
|
x = f ( t , u 1 , u 2 , |
u 3 , u 4 , u 5 , , u 7 , u 8 , u 9 , u 10 ) |
– Т 1 |
|
x = f ( t , u 1 , u 2 , |
u 3 , u 4 , u 5 , , u 7 , u 8 , u 9 , u 10 ) |
– Т 2 |
|
x = f ( t , u 1 , u 2 , |
u 3 , u 4 , u 5 , , u 7 , u 8 , u 9 , u 10 ) |
– Т 3 |
|
x = f ( t , u 1 , u 2 , |
u 3 , u 4 , u 5 , , u 7 , u 8 , u 9 , u 10 ) |
– Т 4 |
|
x = f ( t , u 2 , |
u 3 , u 4 , u 5 , u 6 , u 7 , u 8 , , u 10 ) |
– Т 5 (18) |
|
x = f ( t , , u 2 , |
u 3 , u 4 , u 5 , u 6 , u 7 , u 8 , , u 10 ) |
– Т 6 |
|
x = f ( t , , u 2 , |
u 3 , u 4 , u 5 , u 6 , u 7 , , , u 10 ) |
– Т 7 |
|
x = f ( t , , u 2 , |
u 3 , , u 5 , u 6 , u 7 , u 8 , , u 10 ) |
– Т 8 |
|
x = f ( t , u 1 , u 2 , |
u 3 , u 4 , u 5 , u 6 , u 7 , u 8 , , u 10 ) |
– Т 9 |
Поясним наши обозначения. Наиболее темным цветом ( u 1 ) обозначены переменные, которые оказывают самое сильное влияние на x (возможно, функциональная зависимость). Менее темное обозначение ( u 1 ) говорит о более слабом влиянии переменной на x (возможно, стохастическая зависимость), более слабое влияние на x оказывают и 1 и и 1 . T i , где i = 1,9, -интервалы существования соответствующих зависимостей. Таким образом, в реально действующих процессах подобного рода роли значения переменных существенно изменчивы. Из приведенных выше зависимостей видно, что некоторые переменные могут утрачивать свое значение, а некоторые утрачивают, а потом восстанавливаются, а некоторые новые переменные появляются впервые, как например u 6 , u 7 .
Если сохранить математический «облик» интерпретации функции многих переменных как точку многомерного пространства, то мы приходим к наличию пространства дробной размерности F X . Вычисление размерности F X можно осуществить, например, так:
n - 1 dim F X = ( n + 1) - ^ Х , ^, (19)
i=i где n - размерность вектора и; Xi i+1 означает «силу» стохастической связи между ui и ui+1.
В принципе, могут быть предложены и другие схемы вычисления размерности пространства. Например, n-1
dim F ( n + 1) - E X^, (20)
i = 1
где X 1 i + 1 - зависимость всех компонент вектора и от одной компоненты u 1 .
При достаточно внимательном анализе разложения функций в ряды уместно вспомнить фразу В. И. Арнольда из замечательной книги «Теория катастроф» [11]: «Вычисление в этих прикладных1 исследованиях обычно проводилось без общей теории за счет правильного отбрасывания одних членов ряда Тейлора и оставления других, наиболее важных. Из физиков, особенно систематически применявших теорию катастроф до ее возникновения, стоит особо выделить Л. Д. Ландау. В его руках искусство отбрасывать “несущественные” члены ряда Тейлора, сохраняя
меньшие по величине “физически важные” члены, дало много включаемых в теорию катастроф результатов».
При наличии нескольких выходных переменных процесса он может быть представлен следующим образом.
На рис. 2 показаны два Н -процесса по каналам « x 1 - и », « x 2 - и ». Как видно, эти Н -процессы не пересекаются в пространстве входных-выходных переменных. Из этого следует, что оба задающие воздей- **
ствия x 1 и x 2 не могут быть достигнуты одновременно при управлении этой системой по u . На рис. 3 показаны пересекающиеся Н -процессы по тем же самым каналам [12].
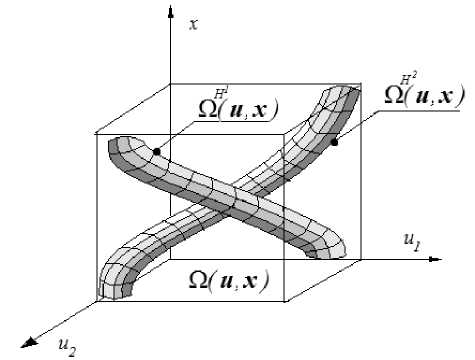
Рис. 2. Непересекающиеся Н- процессы
Из рис. 3 видно, что у двух Н -процессов есть со- 12 вместная подобласть G ( и , x ) = Q ( и , x ) о Q ( и , x ). Именно в этой области Н следует искать задающие воздействия x 1* и x 2* . Для этого сформируем из исходной обучающей выборки { x i , u i , i = 1, 5 } элементы, принадлежащие области GH ( u , x ). Эту выборку обозначим через { x j , u j , j = 1, sG , sG << 5 } . На ее основании строится оценка задающего воздействия:
s G k
2 ^П ф
* i = 1 r = 1
Xj= — 7
2П ф
и Г - и '
cu
n
П Ф
J q = 1
r
cu
n
П Ф
J q = 1
1 Здесь речь идет о теории упругости.
^ q.
V
q
Ц /
^^^^^^в
и q) 1 i
c Ц
^^^^^^в
5 j
q
1 i
c 1
V 5 J
, j = 1,2. (21)
Непараметрический алгоритм дуального управления многомерной безынерционной системой примем в виде [13; 14]:
„ <1> Us
sG
2 и < 1 > Ф
/ = 1
( *<1> * A xs - xj cx
n
ПФ q=1
Ц q -Ц q j c. 1
sG
2 Ф j=1
( *<1> * Л x5 - xj cx
. (22)
n
П Ф q=1
Ц 5 -Ц j c Ц
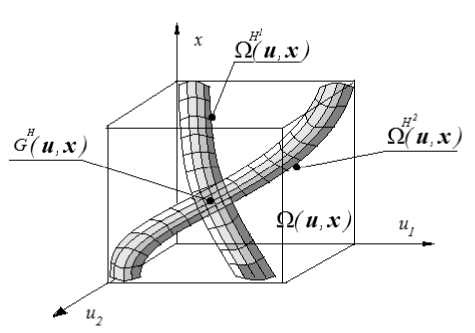
Рис. 3. Пересекающиеся Н -процессы
Второе значение управляющего воздействия может быть оценено с учетом уже найденного первого:
u
< 2 >
s
sG
X « < 2 > Ф j = 1
( *< 2 > *
x s - x j
С x cs
ПФ
J q = 1
^'...
. c*
Ф
(>us
-
< 1 > j
cu J
sG
ХФ j=1
( *< 2 > *
x s - x j
n
П Ф
J q = 1
-
v-q
V q
Ф
( <1 > U s
-
< 1 >A u j
, (23)
sG
j = 1
< k >
Ms
X u < > Ф
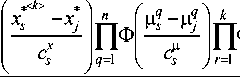
(« ? >
V
u cs
< r >
"“/
u cs
J
sG
Хф( x*
n
- x* )ПФ
7 q = 1
c
v q -v q
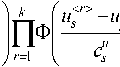
< r > A
J
.
Как видно из (24), все последующие значения управления вычисляются с учетом предыдущих. Таким образом, алгоритмы управления многомерными Н -процессами представляют собой цепочку соотношений (21)–(24).
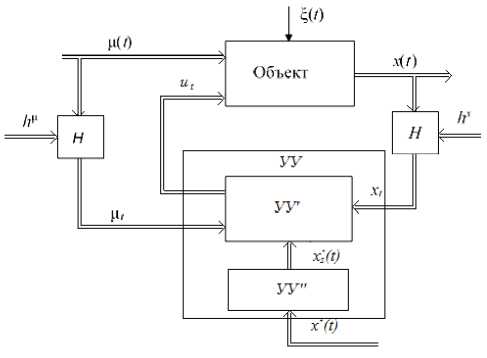
Рис. 4. Матричная система управления Н -процессами
Матричная система управления многомерным безынерционным объектом показана на рис. 4, где представлены следующие обозначения: УУ – управляющие устройства, УУ ‘ блок расчета управляющих воздействий, УУ" - блок расчета задающих воздействий. Такими образом, вышеприведенная схема иллюстрирует функционирование системы управления многомерным безынерционным Н -процессом при фиксированном неуправляемом входном воздействии μ .
Заключение. Итог статьи состоит в анализе особенностей, возникающих при моделировании процессов «трубчатой» структуры, которая имеет место всегда, если компоненты вектора входных переменных процесса стохастически зависимы. В этом случае традиционно [15] используемые модели статических систем с запаздыванием неприменимы или могут приводить к значительным ошибкам. Наиболее интересным является тот факт, что мы приходим к необходимости введения пространства дробной размерности. Безусловно, важным является факт исчезновения и появления роли некоторых входных переменных в различные периоды времени на значения выходных переменных процесса, что тесно связано не столько с пространством дробной размерности, сколько с пространством изменяющейся размерности.
При управлении многомерными Н -процессами сначала необходимо определить соответствующие задающие воздействие для выходных переменных, а уже затем использовать непараметрические алгоритмы управления, которые названы матричным A m - регулятором. Это является существенной особенностью построения управляющей системы в отличие от традиционных алгоритмов управления многомерными безынерционными системами. В настоящей статье все Н -процессы, показанные на рис. 1–3, из соображений простоты визуализации рассматриваются в трехмерном пространстве и в «застывшем» виде. На самом деле, приведенные Н- модели и алгоритмы управления функционируют, когда реальные процессы находятся в движении.
Список литературы Об управлении H-процессами
- Medvedev A. V. Nonparametric approximation in adaptive systems theory//Works of Applied Methods of Statical Analysis. Simulation and Statistical Inference. Novosibirsk: SFU, 2011. С. 195-212.
- Медведев А. В. Анализ данных в задаче идентификации//Компьютерный анализ данных и моделирование. Минск: БГУ, 1995. Т. 2. С. 201-206.
- Медведев А. В. Теория непараметрических систем. Моделирование//Вестник СибГАУ. 2010. Вып. 4(30), С. 4-9.
- Медведев А. В. H-модели для безынерционных систем с запаздыванием//Вестник СибГАУ. 2012. Вып. 5(45), С. 84-89.
- Кошкин Г. М., Пивен И. Г. Непараметрическая идентификация стохастических объектов: науч. изд. Хабаровск: Российская академия наук, Дальневосточное отделение, 2009. 336 с.
- Васильев В., Добровидов А., Кошкин Г. Непараметрическое оценивание функционалов от распределений стационарных последовательностей. М.: Наука, 2004. 512 с.
- Катковник В. Я. Непараметрическая идентификация и сглаживание данных: метод локальной аппроксимации. М.: Главная редакция физико-математической литературы, 1985. 336 с.
- Хардле В. Прикладная непараметрическая регрессия. М.: Мир, 1993. 349 с.
- Айвазян С. А., Енюков И. С., Мешалкин Л. Д. Прикладная статистика, исследование зависимостей. М.: Финансы и статистика, 1985. 488 с.
- Мондельброт Б. Фрактальная геометрия природы. М.; Ижевск: Ижевский институт компьютерных исследований: НИЦ «Регулярная и хаотическая динамика», 2010. 656 с.
- Арнольд В. И. Теория катастроф. М.: Наука, 1990. 128 c.
- Медведев А. В., Михов Е. Д. О компьютерном исследовании Н-моделей//Вестник СибГАУ. 2014. № 3(55). C. 107-113.
- Медведев А. В. Непараметрические системы адаптации. Новосибирск: Наука, 1983. 173 с.
- Медведев А. В. Основы теории адаптивных систем/СибГАУ. Красноярск, 2015. 525 с.
- Методы классической и современной теории автоматического управления: учебник. В 5 т. Т. 3. Синтез регуляторов систем автоматического управления. 2-е изд., перераб. и доп./под ред. К. А. Пупкова и Н. Д. Егупова. М.: Издательство МГТУ им. Н. Э. Баумана, 2004. 616 с.


