Об управлении объектами с памятью в условиях непараметрической неопределенности
Автор: Банникова Анастасия Владимировна, Медведев Александр Васильевич
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 5 (57), 2014 года.
Бесплатный доступ
Рассматриваются проблемы идентификации и управления стохастическими объектами с дискретнонепрерывным характером технологического процесса. Исследуется более общий класс динамических объектов, в дальнейшем - объекты с памятью. Характерной отличительной особенностью рассматриваемых процессов является тот факт, что при описании не используются разностные аналоги дифференциальных уравнений, принятые в классической теории идентификации и управления. Подобные процессы часто имеют место в различных контурах управления аэрокосмической техники, например, при виброиспытаниях космических аппаратов, в процессе их производства. В этом случае локальный канал «вибратор - космический аппарат (КА)», определяемый вибросигналом и соответствующим сигналом датчика, установленным на КА, может описываться разностными уравнениями. При этом естественно отсутствие аналогии между уравнением в непрерывном времени и разностным. Данная особенность является главным отличием объектов с памятью от традиционных динамических процессов. Это накладывает свой отпечаток при моделировании и управлении подобными объектами и обусловливает актуальность рассматриваемой задачи. Рассматриваются теорити- ческие сведения о непараметрических алгоритмах идентификации и управления. Непараметрические модели для объектов с памятью рассматриваются в двух вариантах. Один из них тесно связан с описанием объекта в виде интеграла Дюамеля. Второй путь состоит в частичной параметризации объекта, т. е. соответствует условиям как параметрической, так и непараметрической неопределенности. В основу построения непараметрических алгоритмов дуального управления положены принципы построения стохастических оптимальных систем А. А. Фельдбаума в их байесовской постановке. Состоят они в том, что управляющие устройство должно выполнять две функции: изучение и управление в процессе активного накопления информации. Рассматривается ситуация, когда на входе объекта «включается» управляющие устройство, соответствующие его обратной модели. Очевидно, что описание объекта не может быть по ряду причин точным, и обратный оператор может только приближенно описывать процесс в направлении «выход-вход». На этой основе выстраиваются как непараметрические модели объектов с памятью, так и непараметрические алгоритмы дуального управления. Тщательно анализируется процесс обучения системы дуального управления с активным накоплением информации. Подробно приводятся результаты численного исследования непараметрических моделей для многомерных процессов с памятью, а также результаты вычислительного эксперимента применения алгоритма непараметрического адаптивного дуального управления.
Объект с памятью, априорная информация, а priory information, непараметрическая идентификация, стохастический процесс, дуальное управление
Короткий адрес: https://sciup.org/148177361
IDR: 148177361 | УДК: 519.87
Текст научной статьи Об управлении объектами с памятью в условиях непараметрической неопределенности
Введение . Проблемы моделирования и идентификации сложных промышленных объектов традиционно имеют высокую практическую значимость. В большинстве случаев реальные технологические процессы можно отнести к классу динамических. В частности, такого рода процессы типичны для космической отрасли, например, при изготовлении отдельных узлов и блоков КА и изделий электронной техники (транзисторы, диодные матрицы, микросхемы и др.). Традиционно динамические объекты описываются дифференциальными уравнениями или их разностными аналогами [1; 2], но следует отметить, что такого рода описание объектов с памятью не является единственным. Из-за недостатка априорной информации часто не удается выбрать параметризованную структуру модели исследуемого процесса. В этом случае оказывается эффективным использовать теорию непараметрических систем моделирования и управления [3; 4]. В ряде случаев исследователь находится в условиях, когда априорная информация об исследуемом объекте соответствует одновременно как параметрическому, так и непараметрическому уровням априорной информации [5]. Ранее [6; 7] были рассмотрены некоторые задачи моделирования и идентификации для объектов с памятью. Дальнейшее внимание будет сосредоточено на непараметрических алгоритмах дуального управления [8; 9].
Постановка задачи идентификации . Пусть объект представляет собой динамическую систему и описывается уравнением xt = f ( xt - 1 , xt - 2 , ..., xt - k , ut ), где f ( . ) – неизвестный функционал; xt – выходная переменная процесса; ut – управляющее воздействие; k – известная «глубина» памяти [8], так или иначе найденная на основании имеющейся априорной информации. Здесь существенным является то, что вид функционала не определен с точностью до параметров.
Блок-схема рассматриваемого динамического процесса представлена на рис. 1, где приняты следующие обозначения: xˆt – выход модели объекта, (t) – непре- рывное время, индекс t – дискретное время, hut , hxt
–
случайные переменных помеха.
Контроль
помехи измерений соответствующих процесса, ξ(t) – векторная случайная переменных осуществляется через ин- тервал времени At. Таким образом, можно получить исходную выборку входных-выходных переменных {xi, ui, i = 1,5}, где s — объем выборки, индекс h у переменных объекта из соображения простоты опущен. Следует отметить, что в данном случае параметрическая структура рассматриваемого процесса нам неизвестна, но можно говорить о частичной параметризации модели исследуемого процесса.
Схема, изображенная на рис. 1, является близкой к классической схеме, рассматриваемой в теории управления [10]. Как было замечено ранее, рассмотрение динамического процесса с помощью данной схемы не является единственным, так как одна из переменных процесса, например xt- 2 , может отсутствовать, а конечное выходное воздействие может зависеть только от переменных xt- 1, xt- 3 и входного воздействия u, : x t = f ( xt - 1 , xt _ 3 ,ut ). Таким образом, схема примет вид, изображенный на рис. 2.
Непараметрическая идентификация. В настоящее время наиболее развитой является теория параметрических систем, которая предполагает предварительную параметризацию модели [2; 10]. В случае недостатка априорной информации об исследуемом объекте, часто не представляется возможным обоснованно выбрать параметрическую структуру модели. В этом случае исследователь вынужден, обрабатывая имеющиеся выборки входных-выходных переменных, «добывать» дополнительную информацию, которая позволит более обоснованно выбрать параметрическую структуру модели.
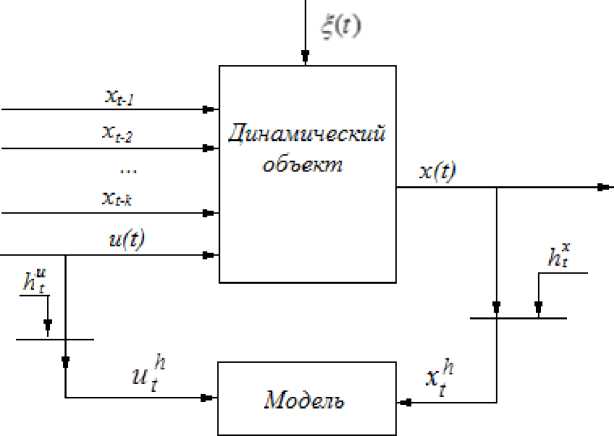
Рис. 1. Блок-схема моделирования объекта с памятью
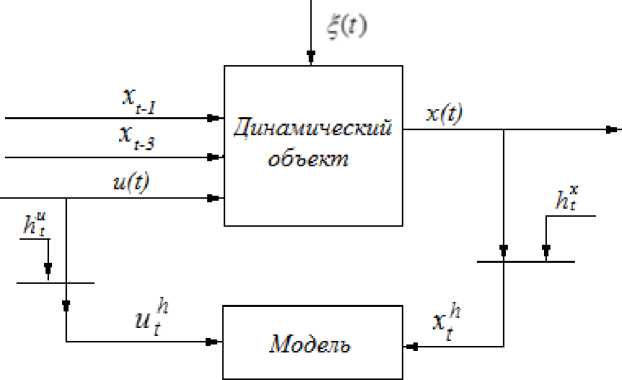
Рис. 2. Блок-схема моделирования объекта с памятью при фиксированных запаздывающих на соответствующее число тактов выходных переменных
В случае, когда априорной информации недостаточно, естественно использовать теорию непараметрической идентификации [11]. Непараметрическая теория, в отличие от предыдущей, предполагает, что известны только качественные характеристики системы. Это позволяет полностью уйти от вопроса определения параметрической структуры объекта.
В классическом случае, изображённом на рис. 1, задача идентификации состоит в оценивании класса операторов на основе выборки {xi, ui, i = 1, s}. В случае, когда динамический объект описывается дифференциальным уравнением при последовательной дискретизации, итоговое разностное уравнение будет содержать последовательно все переменные: xt-1,xt-2,...,xt-k. Тогда в качестве непараметрической модели объекта можно использовать модель, в которой все коэффициенты разностного уравнения будут учтены:
5 - 1
Z V Ф(
u
ui
x 5 ( u , Ю =
i = 1
cs
)Ф(
X - 1
xi
cs
) х
s
Z Ф(
u
ui
i = 1
cs
)Ф(
x 5 - 1
xi
cs
) х
х Ф(
x
x i - 2
cs
)...Ф(
x 5 - k
xi- k
cs
)
х Ф(
x
x i - 2
cs
)...Ф(
x 5 - k
X i - k
cs
-
)
Если для первого случая (рис. 1) выбор непараметрической модели не представляет труда, то какой вид модели следует выбрать для второго случая? При выборе модели для процесса, представленного на рис. 2, мы можем применить модель следующего вида:
5 - 1
Z Xi- Ф(
u
ui
x 5 ( u 5 )
i = 1
c
)Ф( x ? -1— x -L
) х
Z„,/ u5 - и, - x -u
Z Ф(-)Ф(-^-1---i-l) х i=1 c5 c5
ХФ(x ’ x ’ )Ф(x5 3 x-3) cscs хФ( X5-2 - xi-2 )Ф(X5-3 - Xi-3 ) ’ cscs
где последовательно учтены все запаздывающие на соответствующие число тактов выходные переменные. Но, вообще говоря, динамические процессы могут описываться разностными уравнениями несколько другой природы: x t = f ( xt ч, xt _ 3 , ut ), и в этом случае модель может быть принята в виде (3), где учтены только выходные переменные, непосредственно от которых зависит выход процесса:
£X • Ф(u u)Ф(X?-1 - xi-1 )Ф(xx x5 (u?) = ^-----c-------c---------c---- (3)
Z Ф( us u £)Ф( x - x V - L )Ф( x 3 x - S )
i =1 C5 C5
В моделях (1)-(3) Ф ( " ) - ядерная колоколообразная функция [12], c 5 - коэффициент размытости ядра, которые удовлетворяют условиям сходимости [13].
В качестве колоколообразной функции Ф ( - ) [12] могут быть использованы различные ядра. Параметр размытости c 5 при наличии обучающей выборки находится из задачи минимизации показателя соответствия выхода объекта и выхода модели, основанного на методе скользящего экзамена, когда в модели (1)-(3) по индексу i исключается k -е наблюдение переменной, предъявляемой для экзамена:
R(С) = Z(xs (uk)- xk) = min,k * v, k=1
где индекс i фигурирует в формулах (1)-(3).
Для оценки полученных моделей была использована квадратичная ошибка:
1 ,2
R 5 = ~Z( X" X ( u i ) ) , (5) 5 i = 1
где X i - измеренное значение выходной переменной; Х5 - полученная оценка; R 5 - квадратичная ошибка. Также для каждой модели вычисляется относительная ошибка, равная отношению квадратичной ошибки к дисперсии выходной переменной:
W = R 5 / D 5 , (6)
где D5 - дисперсия выходной переменной.
Проверим различие двух представленных моделей в ходе численного исследования. Пусть исследуемый объект является динамическим и описывается уравнением вида
x ( t ) = 0,1 • x ( t - 1) - 0,2 • x ( t - 3) + u ( t ) , (7) где x ( t ) - выходная переменных процесса; u ( t ) -входная переменная процесса. Переходная характеристика данного объекта имеет вид, представленный на рис. 3.
Пусть входное воздействие имеет вид: u ( t ) = sin(0,5 • t ). Модель объекта, полученная с помощью оценки (3), представлена на рис. 4.
В данном эксперименте квадратичная ошибка моделирования равна 0,0089. Как можно увидеть из рис. 4 и значения квадратичной ошибки, полученная модель достаточна качественная и модели вида (3) могут эффективно использоваться при идентификации подобных процессов.
На рис. 5 представлены выход объекта и выход модели объекта, полученной с помощью модели (2).
Квадратичная ошибка в данном случае равна 0,156. Как видно из полученных графиков, данную модель также можно назвать удовлетворительной, хотя очевидно, что она уступает первой.
На рис. 6 представлены выход объекта и модели объекта, полученной при использовании уравнения (3) при уровне помех 7 %.
В эксперименте, представленном на рис. 6, квадратичная ошибка моделирования равна 0,07. Из рисунка 6 и значения квадратичной ошибки можно сделать вывод, что с помощью модели (3) можно получить адекватные модели даже при достаточно высоком уровне помех.
На рис. 7 представлен выход модели объекта и модель объекта, полученная с помощью модели (2) при уровне помех 7 %.
Непараметрическое дуальное управление. Недостаток априорной информации об объекте приводит к необходимости совмещать изучение объекта и управление им. При таком управлении управляющие воздействия носят двойственный характер. Они служат средством изучения, познавания объекта, но также и средством приведения объекта к требуемому состоянию. Такое управление называют дуальным управлением [8]. Дуальное управление было открыто А. А. Фельдбаумом и развито на основе теории статистических решений.
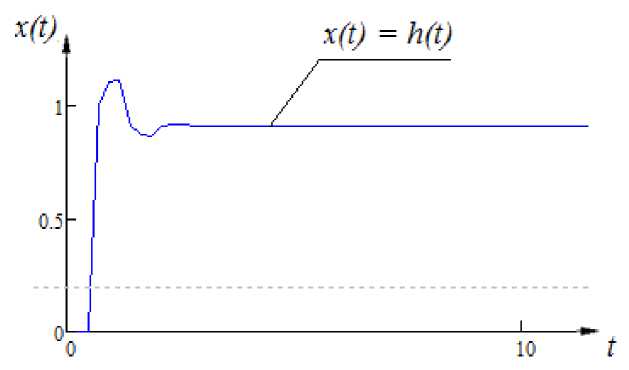
Рис. 3. Переходная характеристика объекта процесса (7)
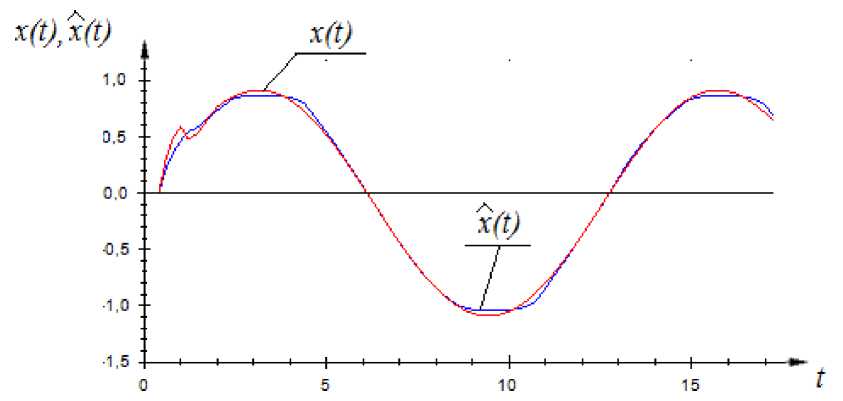
Рис. 4. Результаты моделирования объекта с памятью при частично известной параметрической структуре с помощью оценки (3)
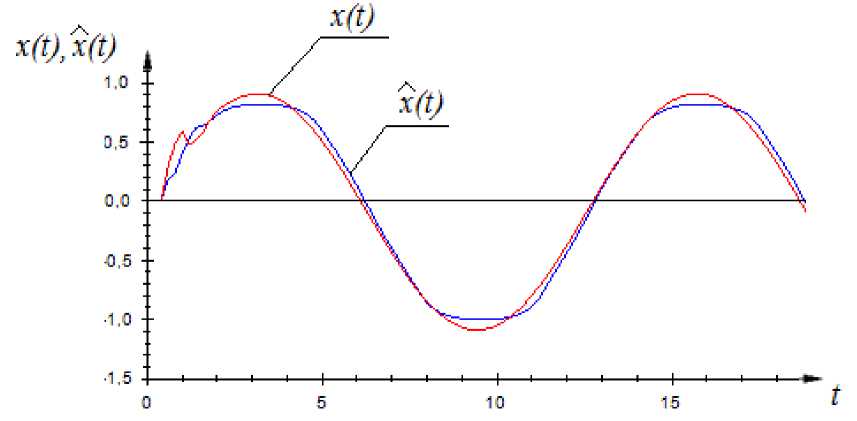
Рис. 5. Результаты моделирования объекта с памятью при частично известной параметрической структуре с помощью оценки (2)
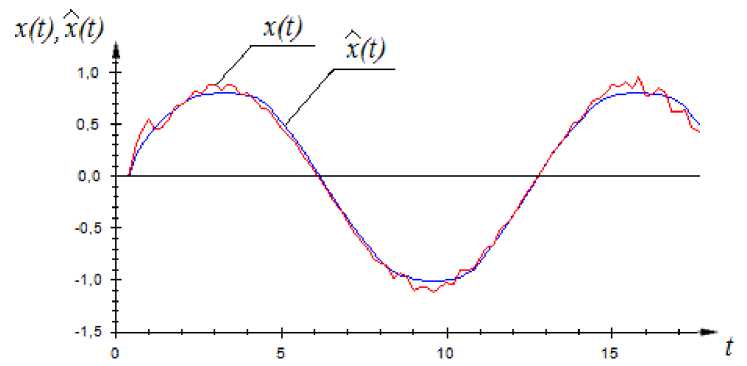
Рис. 6. Результаты моделирования объекта с памятью при частично известной параметрической структуре модели при помехе 7 % с помощью оценки (3)
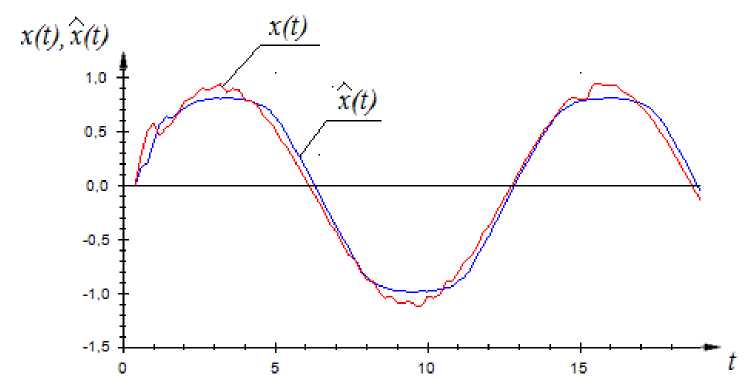
Рис. 7. Результаты моделирования объекта с памятью при помехе 7 % при частично известной параметрической структуре модели с помощью оценки (2)
x(t)
X?
x(t)
Пусть объект представляет собой динамическую систему и описывается уравнением xt= f(xt-1, xt-3,ut). Схема управления представле- на на рис. 8.
Непараметрический алгоритм дуального управления, подробно описанный в [14; 15], имеет вид us+1=us* + Δus+1,
где в ^ us * сосредоточены «знания» об объекте; Δ us + 1 – «изучающие» поисковые шаги:
Δ us + 1 = ε( xs * + 1 - xs ).
В этом и состоит дуализм алгоритма (8).
Составляющая us* из^ (8), также как и в случае непараметрической идентификации, представляет собой сложный вопрос. С одной стороны, мы также как и в (2) можем учитывать все переменные до высшего порядка:
s ∑ u i ⋅Φ ( i = 1
* x s + 1
xx - x i ) Φ ( s - 1 i - 1
) ×
∑ s Φ ( x s * + 1 - x i ) Φ ( x s - 1 - x i - 1 ) × i = 1 с s с s
×Φ ( x s - 2 - x i - 2 ) Φ ( x s - 3 - x i - 3 ) сsсs
×Φ(xs-2-xi-2)Φ(xs-3-xi-3) сsсs где x* – задающее воздействие, либо учитывать только переменные, непосредственно от которых зависит выход объекта:
*
∑s x-xx-x ui ⋅Φ(s+1i)Φ(s-1i-1
i = 1 с s с s
) Φ ( x s - 3 - x i - 3 )
∑ s Φ ( x s * + 1 - x i ) Φ ( x s - 1 - x i - 1 ) Φ ( x s - 3 - x i - 3 ) i = 1 сsсsсs
. (11)
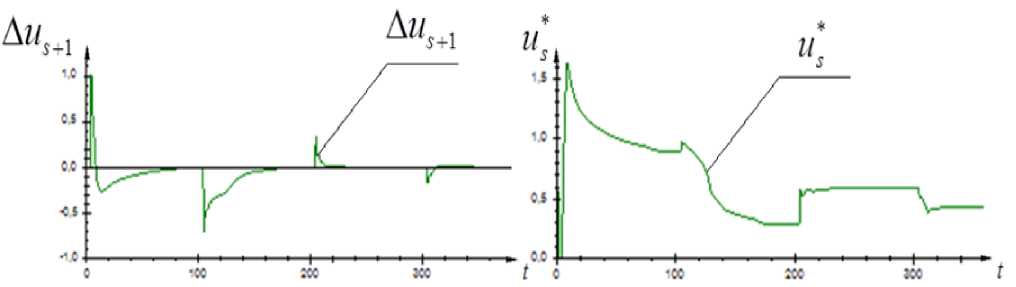
Проанализируем характер дуализма алгоритма (8). На начальной стадии управления основная роль принадлежит второму слагаемому Δ us + 1 из формулы (8). Это случай активного накопления информации в системе дуального управления, который начинается с появления первого наблюдения входной и выходной переменных объекта. По мере процесса обучения (накопления информации) всё возрастающую роль при формировании управляющего воздействия us + 1 начинает^ играть первое слагаемое, т. е. us * . Таким образом, в процессе дуального управления объектом фигурируют как этап изучения объекта, так и этап приведения его к цели.
Исследуем различие между двумя подходами в ходе численного эксперимента. Пусть исследуемый объект является динамическим и описывается уравнением вида
x ( t ) = 0,4 ⋅ x ( t - 1) - 0,3 ⋅ x ( t - 3) + u ( t ) , (12)
где x ( t ) – выходная переменных процесса; u ( t ) – входная переменная процесса. Переходная характеристика данного процесса представлена на рис. 9.
Пусть входное воздействие имеет вид u ( t ) = sin(0, 5 ⋅ t ) , а управляющее воздействие, поступающее на вход объекта с управляющего устройства, описывается уравнением (8), где us * равно (11). Пусть задание имеет вид ступенчатой функции. В таком случае результат управления имеет вид, представленный на рис. 10.
На рис. 11 представлены результаты управления при помехе 5 %.
На рис. 10 квадратичная ошибка управления равна 0,072, на рис. 11 – 0,13. Сравним полученные результаты со случаем, когда us * будет равно (10) (рис. 12).
Квадратичная ошибка управления для случая, представленного на рис. 11, равна 0,15. Как мы можем заметить, также как и в случае непараметрической идентификации, непараметрическое управление оказывается намного эффективней, тогда как в формуле управляющего воздействия, поступающего на объект, учитываются только переменные, которые формируют выходное воздействие.
Рассмотрим работу непараметрического дуального алгоритма управления подробнее. Обучение управлению начинается с первой диады наблюдений. На начальной стадии управления необходимо некоторое время (накопление выборки) для приведения объекта в заданное состояние, но уже на следующих этапах работы алгоритм почти мгновенно достигает задания. На рис. 13 подробно представлено поведение слагаемых алгоритма дуального управления.
На рис. 14 показано, как ведет себя алгоритм при случайном задании. Видно хорошее качество управления с помощью непараметрического регулятора даже при таком «экзотическом» варианте, когда задание носит случайный характер. С подобной задачей не справится ни один из известных регуляторов. На практике такой вариант задающего воздействия не встречается, однако это представляет интерес с теоретической точки зрения.
Непараметрическая идентификация на основе интеграла Дюамеля. Пусть объект описывается линейным дифференциальным уравнением неизвестного порядка. В этом случае при нулевых начальных условиях x ( t ) [5] находится как
t
x ( t ) = ∫ h ( t - τ) u (τ) d τ, (13) 0
где h ( t - τ) весовая функция системы, является производной переходной функции k ( t ), т. е. h ( t ) = k ′ ( t ). Известно, что обратным оператором (13) является оператор [5]
t
u ( t ) = ∫ ν ( t - τ ) x (τ ) d τ , (14) 0
где v ( t - т) - весовая функция объекта в направлении «выход-вход» и v ( t ) = ю ' ( t ), где ю( t ) - переходная функция системы в том же направлении. В этом случае A представлен оператором (13), а A - 1 - выражением (14). Следовательно, теперь проблема состоит в отыскании весовых функций h ( t ), v ( t ). Один из возможных путей решения этого вопроса состоит в снятии переходной характеристики на реальном объекте с последующей оценкой его весовой функции по результатам измерений { x i = k i , t i , i = 1, s }.
Непараметрическая модель (13) будет иметь вид
X s ( t ) = j h s ( t - т, k s , 1 ) u (т) d т, (15)
где ks,ts - временные векторы: ks = (k1, ..., ks), ts = (t1, -, ts); hs (•) равна hs (t) =
t
ЬФ
Hc s 0
t - t i
c
где H ( • ) - колоколообразные (ядерные) функции [12], cs - параметр размытости, удовлетворяющие некоторым условиям сходимости [13]. Предлагается переходную функцию v ( t ) получить на модели в направлении «выход-вход», т. е. «вспять». Таким образом, из соотношения
t xs ( t ) = 1( t ) = J hs ( t - т, ks , ts ) u ( т ) dт (17)
можно получить выборки { u i , t i , i = 1, s } .
Пусть исследуемый объект является динамическим и описывается уравнением вида:
x ( t ) = 0,9 • x ( t - 1) - 0,25 • x ( t - 3) + 0,19 u ( t ). (18)
Переходная характеристика данного процесса представлена на рис. 15.
Пусть входное воздействие имеет вид u ( t ) = sin(0,5 • t ). Модель объекта получена при использовании уравнения (15) (рис. 16).
s
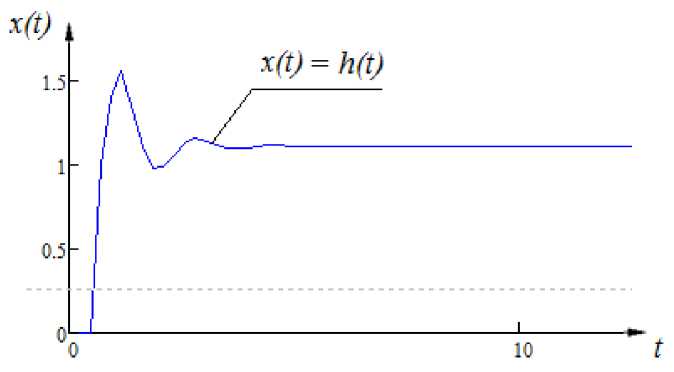
Рис. 9. Переходная характеристика процесса (12)
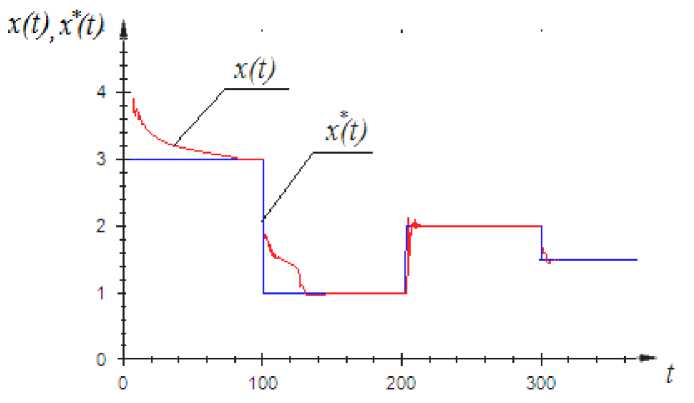
Рис. 10. Результат управления при частично известной параметрической структуре при входном воздействии, описанном уравнением (11)
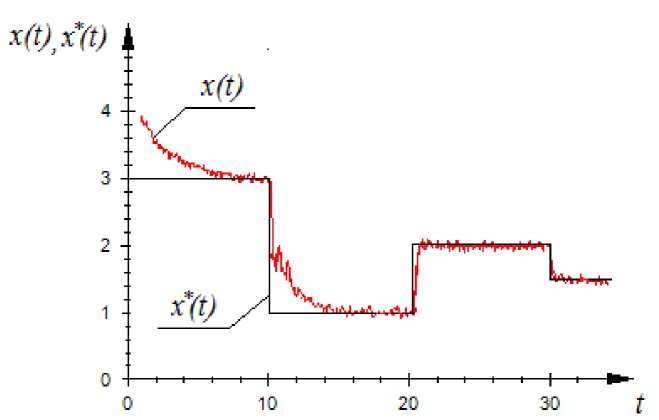
Рис. 11. Результат управления при частично известной параметрической структуре, при помехе 5 %
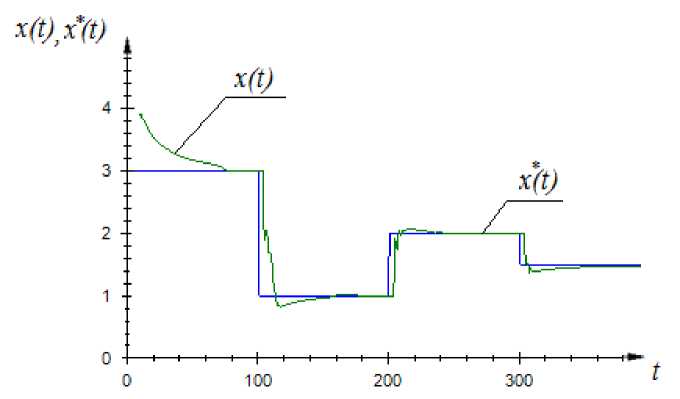
Рис. 12. Результат управления при неизвестной параметрической структуре
а
б
Рис. 13. Поведение составляющих управляющего воздействия
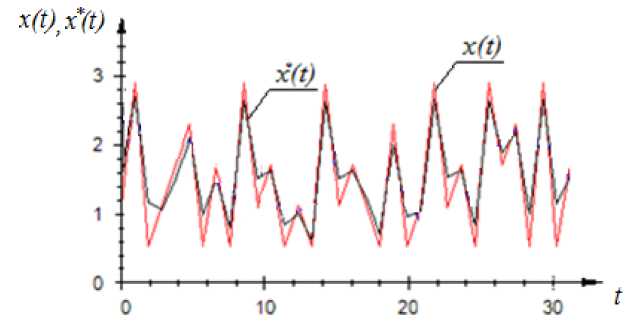
Рис. 14. Результаты управления при случайном задании
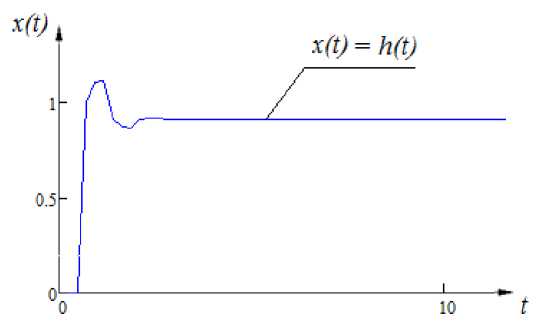
Рис. 15. Переходная характеристика процесса (18)
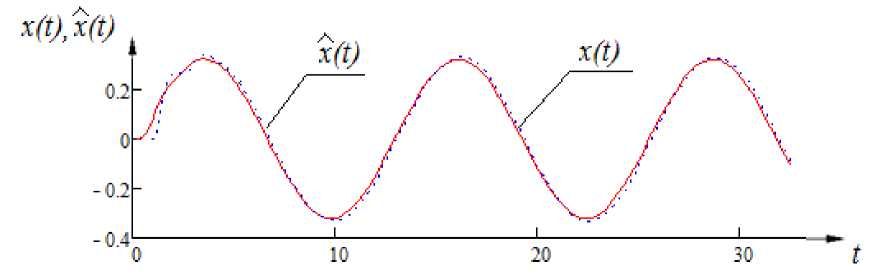
Рис. 16. Результаты моделирования объекта с памятью при использовании интеграла Дюамеля
Непараметрическое управление на основе интеграла Дюамеля. В условиях непараметрической неопределённости [15] уравнение процесса с точностью до вектора параметров неизвестно, но известны свойства объекта качественного характера, например, однозначность характеристик или неоднозначность для безынерционных процессов; линейность или тип нелинейности для динамических. Если вид уравнения, описывающего процесс, неизвестен, то известные параметрические методы теории управления не применимы для решения задач идентификации и управления.
Введем оператор объекта A , описывающий процесс, т. е.
x ( t ) = A < u ( t ) > , (19)
где u ( t ) - управляющие воздействие; x ( t ) — выходная переменная объекта.
Если существует оператор, обратный A , т. е. А -1, А -1 А = 1 - единичный оператор, то
А - * x ( t ) = А - 1 A < u ( t ) > , u ( t ) = A - 1 x ( t ) . (20)
Таким образом, учитывая, что выход объекта может описываться оценкой (15), непараметрический алгоритм управления линейной динамической системой примет вид
* us(t) = Юs(0)x (t)+ t t/τ
+ — f Е®,ф 'I -Sc s 5 о i I
^^^^^^B
—----- I x * (т) d т, c s J
где x * ( t ) – задающее воздействие. Ясно, что объемы выборок при определении переходных характеристик на реальном объекте и на модели могут не совпадать. Фрагмент работы алгоритма (18) представлен ниже.
Пусть исследуемый объект является динамическим и описывается уравнением вида
x ( t ) = 0,9 ■ x ( t - 1) - 0,25 ■ x ( t - 3) + 0,19 u ( t ), (22)
где x ( t ) – выходная переменных процесса; u ( t ) – входная переменная процесса. Переходная характеристика данного процесса представлена на рис. 17.
Пусть входное воздействие имеет вид u (t) = sin(0,5 ■ t), а задающие воздействие - ступенчатой функции (рис. 18).
Пусть задание имеет вид траектории u ( t ) = sin(0,5 · t ) (рис. 19).
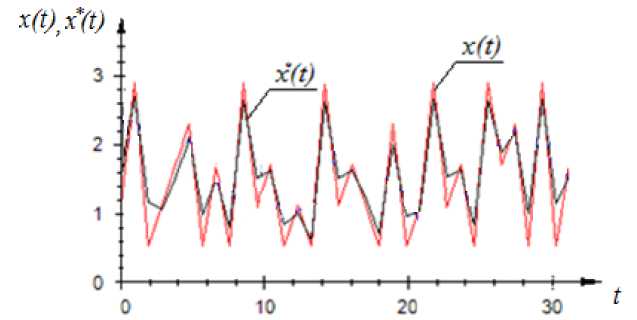
Рис. 17. Переходная характеристика процесса (22)
Рис. 18. Результат управления при применении алгоритма, основанного на интеграле Дюамеля
Заключение. Подводя итог настоящей статьи, следует заметить, что рассматривается очень важная с практической точки зрения задача идентификации в замкнутом контуре для дискретно-непрерывных процессов в условиях непараметрической неопределенности. Одним из основных преимуществ непараметрической теории идентификации и управления по сравнению с доминирующей на сегодняшней день параметрической теорией является тот факт, что первая более применима к задачам практики, так как способна работать в условиях малой информации об объекте. Данные условия характерны для задач моделирования и идентификации в разных отраслях промышленности, в том числе и аэрокосмической индустрии. Актуальность рассмотренной задачи обусловлена тем, уравнение, описывающие динамичесский процесс, не имеет вид разностного аналога дифференциального уравнения. В этом случае исследование процесса построения модели представляет специальный самостоятельный процесс. В статье приводятся непараметрические модели для многомерных дискретно-непрерывных процессов, достаточно подробно изложены результаты численного исследования.
Список литературы Об управлении объектами с памятью в условиях непараметрической неопределенности
- Цыпкин Я. З. Адаптация и обучение в автоматических системах. М.: Наука, 1968. 400 с.
- Эйкхофф П. Основы идентификации систем управления. М.: Мир, 1975. 683 с.
- Медведев А. В. Теория непараметрических систем. Моделирование//Вестник СибГАУ. 2010. № 4 (30). С. 4-9.
- Медведев, А. В. Теория непараметрических систем. Общий подход//Вестник СибГАУ. 2008. № 3(20). С. 65-68.
- Медведев А. В. Непараметрические системы адаптации. Новосибирск: Наука, 1983. 174 с.
- Банникова А. В., Сергеева Н. А. О непараметрическом моделировании стохастических объектов с памятью//Вестник СибГАУ. № 2 (54). 2014. С. 6-10.
- О непараметрическом управлении стохастическими объектами с памятью/А. В. Банникова /Вестник СибГАУ. № 3 (55). 2014. С. 28-35.
- Фельдбаум А. А. Основы теории оптимальных автоматических систем. М.: Физматгиз, 1963. 552 с.
- Медведев А. В. Теория непараметрических систем. Управление-I//Вестник СибГАУ. 2013. № 2 (48). С. 57-63.
- Цыпкин Я. З. Информационная теория идентификации. М.: Наука. Физматлит, 1995. 336 с.
- Медведев А. В. Теория непараметрических систем. Активные процессы -I/Вестник СибГАУ. 2011. № 4 (37). С. 52-57.
- Eddy W. F. Optimum kernel estimators of the mode//Ann. Math. Statist. 1980. Vol. 8. P. 870-882.
- Надарая Э. А. Непараметрические оценки плотности вероятности и кривой регрессии. Тбилиси: Изд. Тбилис. ун-та, 1983. 194 с.
- Медведев А. В. Теория непараметрических систем. Управление-II//Вестник СибГАУ. 2013. № 3 (49). С. 85-90.
- Medvedev A. V. Optimization Techniques IFIP Technical Conference (july 1-7, 1974, Novosibirsk). Springer-Verlag. Р. 48-55.


