Об уравнении Леонтьева для параметра Грюнайзена твердых тел

Параметр Грюнайзена служит характеристикой ангармонизма колебаний решетки и обычно вычисляется по уравнению Грюнайзена из экспериментальных данных о коэффициенте объемного теплового расширения β , изотермическом модуле объемного сжатия В , молярном объеме V и молярной теплоемкости C V :

Y - S BV- -                                           (1)

CV

Это соотношение выводится из уравнения состояния.

Леонтьев выполнил усреднение частоты колебаний решетки ω и непосредственно из определения

γ = – d ln ω / d ln V получил следующее уравнение для параметра Грюнайзена [1]:

^Y = 2

[ bat ] ,

I P^K J

где ВА – адиабатический модуль всестороннего сжатия, ρ – плотность, vK – среднеквадратичная ско- рость звука:

2 _ ^vL ^{+ 2 v}S

VK = g ,

а v_L и v_S – скорости продольной и поперечной акустических волн соответственно.

Формула Леонтьева привлекательна тем, что, в отличие от уравнения Грюнайзена, она позволяет рассчитывать γ по доступным экспериментальным данным о плотности и упругих характеристиках. Ранее было установлено, что соотношение Леонтьева удовлетворительно согласуется с уравнением Грюнайзена [2].

Работа посвящена обсуждению одного допущения, использованного при выводе формулы Леонтьева.

Отмечая удовлетворительное согласие соотношения Леонтьева с уравнениями Грюнайзена, вместе с тем необходимо признать, что его вывод не является безупречным.

Рассмотрим кратко приближенный вариант вывода данной формулы [1]. Из закона сохранения энергии для адиабатического процесса:

СvdT = pdV и из определения коэффициента объемного теплового расширения:

P = 1/V( dV/dT)

следует приближенное выражение:

pV = C y / p .                                        (4)

Для давления используется уравнение:

2 U

p = 3 V ’ где объемная плотность средней энергии теплового движения молекул выражается через среднеквадратичную скорость звука (3):

U

F = ^p v k .

Из последних трех соотношений (4) – (6) вытекает связь тепловых характеристик β и С V со скоростями распространения продольной и поперечной звуковых волн:

C^- = 2 pv 22, (7) eV 3 k которая находится в удовлетворительном согласии с экспериментальными данными [1]. Установление указанной связи является основной задачей работы [1]. С учетом этого равенства (7) в приближении B ≈ BA (Cp ≈ CV) уравнение Грюнайзена (1) переходит в формулу Леонтьева (2). Наряду с приближенным вариантом Леонтьев дает более строгий вывод своей формулы (2). Однако в обоих случаях используется основное уравнение молекулярно-кинетической теории идеального газа (5). В связи с этим возникает вопрос об оправданности применения формулы давления идеального газа к твердым телам, который, на наш взгляд, требует отдельного обсуждения.

Один из вероятных ответов на данный вопрос, по-видимому, заключается в том, что Леонтьев под давлением р в выражении (5) подразумевает фононное давление твердых тел, поскольку, во-первых, он выражает его через скорость звука (6) и, во-вторых, нигде в работе [1] не употребляются термины типа «давление идеального газа», «уравнение кинетической теории газа». Формула (5) записывается после предложения [1]: «Затем применим следующее соотношение классической и квантовой физики для связи давления со средней энергией молекулы», причем без ссылок на какие-либо источники. В самом деле, известно, что фононное давление в твердом теле формально совершенно подобно давлению идеального газа (5) [3]. На поставленный выше вопрос дадим другой вариант ответа, основанный на представлении Френкеля [4, 5] о возможности применения формулы (5) к твердым телам. По-видимому, он фактически аналогичен первому варианту.

Уравнение состояния есть условие баланса, которое требует, чтобы внешнее давление р , совместно с внутренним давлением р i , уравновешивало тепловое давление p t , действующее на поверхность твердого тела изнутри [3–5]:

p + p i = p t .

В идеальном газе не возникает надобности различать его внешнее и тепловое давления, ибо p_i = 0

и p = p t , а в твердом теле ситуация противоположная:

p <<  p i ≈ p t .

В балансе огромных противоборствующих давлений p_i ≈ p_t ≈ 10⁴ атм совершенно теряется внешнее атмосферное давление p = 1 атм.

Френкель отмечает, что «тепловое давление, которое оказывает атом, связанный почти упругим образом в твердом теле, на один из боковых атомов, по своей зависимости от температуры очень похоже на то давление, которое он оказывал бы, будучи совершенно свободным, т. е. если бы мы имели дело не с моделью твердого тела, а с моделью газа» [4, с. 169]. Используя эту идею, он предлагает расчет коэффициента теплового расширения твердого тела, где привлекается формула давления идеального газа (5) и равенство величин p_t и p_i [5]. Причиной теплового расширения по Френкелю с формальной точки зрения является давление:

p = B A V/V,                                    (8)

«численно равное тому внешнему давлению (отрицательного знака), которое могло бы вызвать то же самое изменение объема Δ V при T = 0 K, но приложенное к поверхности тела с внутренней ее стороны» [5, гл. XVI, § 59].

По своей природе это давление р не имеет ничего общего с упругим напряжением, которое им вызывается и уравновешивается. «Будучи непосредственно обусловленным тепловым движением, оно представляет собой не что иное, как равнодействующую сил, испытываемых… внутренними атомами со стороны поверхностных, которые стремятся от них оторваться» [5]. «Если бы взаимная связь атомов внезапно исчезла, то для удержания их в данном объеме V пришлось бы приложить внешнее давление р , которое определяется известной формулой кинетической теории газов» [5]:

pV — — и .                                           (9)

«Поскольку р , определяемое (9), может на самом деле компенсировать силы межатомного сцепления, оно должно совпадать с введенным выше давлением р в формуле (8)» [5].

Таким образом, с этих позиций давление в соотношении (5), по-видимому, можно рассматривать как тепловое давление, которое по величине должно совпадать с давлением в выражении (4), которое имеет смысл внутреннего давления, против которого совершает работу система за счет убыли внутренней энергии при адиабатическом процессе.

Обращает внимание тот факт, что равенство (5) напоминает первый закон Грюнайзена (m и n – параметры потенциала Ми):

( mn ] U

B — I I ,

I 9 J V поскольку модуль объемного сжатия не только пропорционален давлению, но для газов совпадает с ним. Интересно заметить, что сравнение (10) с уравнением Леонтьева (2), записанным в виде:

B A

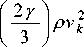
I 2 y ) U_

L 3 J V ’ приводит к формуле для параметра Грюнайзена при BA ≈ B (Cp

C V ):

mn I C p 1 mn

Y —       1 I =         ,

6 L ^c v J 6

которая в первом приближении находится в согласии с экспериментальными данными, в частности для ионных кубических кристаллов ( n ≈ 12, m ≈ 1, откуда γ ≈ 2).

Таким образом, при применении уравнения Леонтьева (2) необходимо иметь в виду, что при его выводе делается не совсем очевидное допущение (5). Однако из приведенных выше соображений следует, что оно вполне приемлемо.