Об ускорении частиц в постоянном магнитном поле и перпендикулярном ему электрическом поле, нарастающем во времени
Автор: Кичигин Г.Н.
Журнал: Солнечно-земная физика @solnechno-zemnaya-fizika
Статья в выпуске: 2 т.7, 2021 года.
Бесплатный доступ
Рассматривается задача ускорения частиц в постоянном однородном магнитном поле В и перпендикулярном ему однородном медленно растущем электрическом поле E. В предположении линейного нарастания электрического поля до максимальной величины Em=В найдены приближенные аналитические соотношения, определяющие зависимость скорости частицы от времени ускорения. Показано, что частицы за все время нарастания электрического поля ускоряются до некоторой конечной энергии, величина которой определяется темпом нарастания электрического поля. Установлено, что чем он меньше, тем больше предельная энергия. В случае Em/В
Ускорение частиц, скрещенные электрическое и магнитное поля, стационарное магнитное поле, переменное во времени электрическое поле, космическая плазма
Короткий адрес: https://sciup.org/142229645
IDR: 142229645 | DOI: 10.12737/szf-72202103
Текст научной статьи Об ускорении частиц в постоянном магнитном поле и перпендикулярном ему электрическом поле, нарастающем во времени
В бесстолкновительной космической плазме ускорение заряженных частиц происходит в основном в электромагнитных полях, существующих в плазме. Один из важных случаев — ускорение частиц в стационарном магнитном и изменяющемся во времени электрическом полях, характерных для различных импульсных процессов в космической среде. Такие ситуации возникают в вспышечных процессах в хромосфере Солнца, межпланетной плазме, магнитосфере и ионосфере Земли. Как правило, изменяющееся во времени электрическое поле — это так называемое поляризационное поле, возникающее при набегании потоков плазмы на области с искривленным магнитным полем. Известный пример — электрическое поле поляризации, возникающей за счет разделения противоположно заряженных частиц при движении ограниченного в пространстве потока плазмы в тороидальном магнитном поле [Морозов, Соловьев, 1963; Альфвен, Фельтхаммар,
1967; Альфвен, 1983; Lindberg, Kristoferson, 1971; Lindberg, 1978]. Указания на возникновение таких полей были получены еще в прошлом веке в лабораторных экспериментах Линдберга [Lindberg, 1978; Lindberg, Kristoferson, 1971] при эжекции потока бесстолкновительной плазмы в искривленное магнитное поле.
Временное изменение электрического поля в за-магниченной космической плазме оказывает большое влияние на модуляцию космических лучей (КЛ) при их распространении в гелиосфере. Для описания модуляционных эффектов КЛ широко используется подход, в котором предполагается, что электромагнитные поля в гелиосфере регулярны и их структура адекватно описывается в рамках модели Паркера [Parker, 1963]. В подобной ситуации определяющим фактором в модуляции КЛ является изменение их энергии при движении в регулярных электромагнитных полях гелиосферы. Изменение же энергии, в свою очередь, определяется величиной и природой электрических полей межпланетной среды и временем взаимодействия частиц с этими полями [Dvornikov, Sdobnov, 2002]. Обстоятельное исследование модуляции КЛ за счет различных факторов, связанных с электромагнитными полями гелиосферы, дано в [Дворников и др., 2013], где показано, что в рамках рассматриваемого подхода теоретические и экспериментальные характеристики модуляции КЛ разумно согласуются.
В данной работе в случае скрещенных полей — стационарного магнитного и переменного во времени электрического — представлены решения релятивистских уравнений движения частиц, которые могут использоваться для нахождения энергии ускоренных частиц в различных импульсных процессах в космической плазме и, в частности, при анализе модуляции КЛ в гелиосфере.
ПОСТАНОВКА ЗАДАЧИИ ИСХОДНЫЕ УРАВНЕНИЯ
Рассмотрим движение заряженной частицы в стационарном однородном магнитном поле В, вектор которого направлен вдоль оси Z, и изменяющемся во времени электрическом однородном поле Е(t), направленном вдоль оси Y. Уравнения, описывающие динамику частиц в таких полях в релятивистском случае, имеют вид dp = qE + q[ vB]/с, mc2 — = qEv. (1)
dt dt
Здесь E и B — векторы электрического и магнитного полей; v, p — векторы скорости и импульса частиц соответственно; q, m — заряд и масса покоя частиц; с — скорость света, γ — безразмерная полная энергия частиц, нормированная на энергию покоя частицы mc2. Здесь и далее обозначение [vB] означает векторное произведение. Поскольку электрическое и магнитное поля взаимно перпендикулярны, мы имеем свободное движение частиц вдоль магнитного поля с постоянной скоростью и двумерное движение в плоскости, перпендикулярной магнитному полю. В этой плоскости уравнения (1) в компонентах примут вид dp = qVyB]c, dp = qE - qVxBk, dt dt mc2 = qEv .
dt y
Здесь v х , v y , p х , p y — х- и у- компоненты скорости и импульса частиц соответственно. Введем безразмерные переменные: τ=ω Bt — безразмерное время, где ω В = qВ /( mс ) — нерелятивистская циклотронная частота; v , w — х- и у -компоненты скорости, нормированные на скорость света.
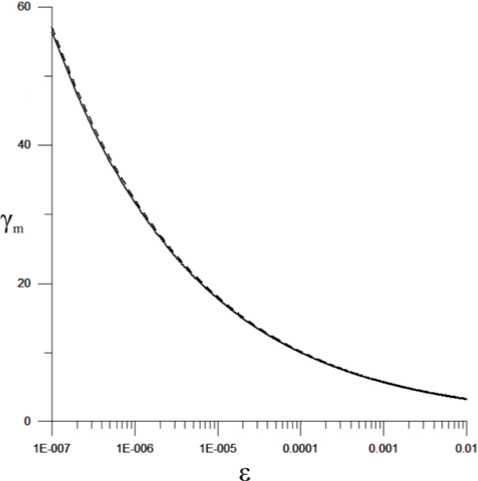
Ниже мы решим эти уравнения для частного случая, когда скорость частицы вдоль магнитного поля равна нулю, а электрическое поле нарастает во времени линейно: Е(t)=Вt/T, где T — время, за которое электрическое поле растет от нулевой отметки до величины B. Предполагается, что электрическое поле нарастает так медленно, чтобы за характерное время, равное циклотронному периоду Tс=2π/ωВ, электрическое поле изменялось незначительно по сравнению с В. Это означает, что n — число циклотронных периодов вращения частицы в магнитном поле B за время Т — должно быть велико: n=1/(2πε) >>1, следовательно, должен быть малым параметр ε=1/(ωВT)=Tс/(2πT)<<1. В реальных ситуациях электрическое поле может нарастать до некоторой максимальной величины Еm В принятом нами линейно нарастающем электрическом поле уравнения для компонент скорости и энергии в безразмерном виде примут вид d (yv) d (yw) ----= w, -----= ST - v, — = STw- d t d t Эти уравнения можно свести к системе уравнений только для компонент скорости dvdw — = w (I-vdv)/y , =[ v d(l-w)-v ]/Y, d t где vd=st = Е/В — безразмерная скорость дрейфа. В нерелятивистском случае (γ=1) система (2) имеет точные аналитические решения, которые при начальном условии v=w=0 запишутся так: v=s(t-sinT), w=s(I-cost). Уравнения (2) также решаются аналитически, если vd=1 [Ландау, Лифшиц, 1967]. В этом случае уравнения (2) имеют вид dY dр dPy Ру =Y w = Y—= Y—, Px =Y v = Y -Y—. d t d t d t Пользуясь этими формулами, получим dpx d y d ( dpy ) Ру =yT" = Y:r-Y:rl Y-p Idt dt dt( dt J При начальных условиях γ=1, рх=ру=0 имеем dру Y—= Y -Px = 1-d t Подставляя в (4) dPy IdY 1 ство Ру J = ,1, d t / d t / f d Y) Y = p„ / I — I получим равен/ k d tJ откуда следует y = P2 / 2 +1- Подставляя γ в (4), получим dPy f РУ J dPy, Y —- = — +1 —- = 1, d t2 k j откуда имеем соотношение [Ландау, Лифшиц, 1967] рУ /6 + Ру =T, из которого следует связь между импульсом ру и временем ускорения. Остальные переменные выражаются через ру: Y = рУ/2 +1, Px = рУ/2, v = рУ/(2 + P2), w = 2ру /( 2 + р2 ) - (6) В общем случае решение системы уравнений (2) можно получить только численными методами. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ (2) В частном случае линейной зависимости Е(t) от времени для численного решения исходных уравнений мы использовали метод Рунге — Кутты. В расчетах параметр е варьировался в интервале значений 10-2>е>10-7, в котором е изменяется в пределах пяти порядков величины. Результаты численных расчетов для е = 10-2 и е = 10-3 представлены на рис. 1, на котором приведены зависимости компонент скорости от времени. Для наглядности показаны зависимости от времени разностей v-vd, w - SYd, где vd, SYd — усредненные по времени значения осциллирующих величин v и w. Видно, что в начале ускорения скорость частиц имеет колебательный характер, а период осцилляций, как и должно быть, совпадает с циклотронным. Очевидно, такое поведение скорости частиц связано с их циклотронным вращением в магнитном поле. В расчетах получено, что пока присутствует ларморовское вращение частиц в процессе их ускорения, удовлетворительно соблюдаются соотношения v « v « V d = st, y«y d = (1-v d2)-1/2, w = sy3. (7) Из рисунка видно, что основная особенность полученных результатов состоит в том, что процесс ускорения частиц разбивается на два этапа. На первом решения имеют осциллирующий характер, и в интервале используемых значений е этот этап длится более 90 % времени ускорения. Видно, что длительность первого этапа возрастает с уменьшением ε, связанного с темпом нарастания электрического поля, а на финальном отрезке осцилляторного этапа период колебаний компонент скорости растет, а амплитуда колебаний падает. Когда амплитуда стремится к нулю, характер решений резко изменяется и начинается второй, апериодический этап временного поведения скорости, на котором временные зависимости компонент принимают апериодический монотонный вид. Как выяснилось при анализе результатов численных расчетов, как на первом этапе, так и на втором, для компоненты скорости w вполне приемлемым по точности оказалось соотношение w=еY3, которое было принято за основу. Нетрудно показать с помощью первой формулы из системы (2), что соотношение w=еY3 можно получить, если положить vvd=v2, v~vd=ет, что и было сделано. Далее из формулы v2=vvd=v2+ w2 с учетом того, что в расчетах w/vd<1, было найдено уточненное выражение для х-компоненты скорости v = vd(1- w2/vd). Таким образом, учитывая соотношения (7) на первом этапе и используя метод подбора подходящих соотношений, которые адекватно описывают временное поведение компонент скорости в численных расчетах на втором этапе, мы пришли к следующему важному заключению: на всем временном участке ускорения, где w/vd<1, разумно подходящими по точности являются следующие приближенные зависимости скорости частиц от времени: Рис. 1. Зависимость от времени (в единицах vd) компонент скорости частиц для е=0.01 и е=0.001. Приведены разности между осциллирующими во времени компонентами скоростей v и w и их усредненными по времени значениями vd и SY3 соответственно v = (vvd )1/2, w = sy3, v = v d(1- w2/v 2). (8) Необходимо отметить, что на осцилляторном этапе ускорения все величины в формуле (8) — средние по времени значения. Величины, определяемые из формулы (8), и полученные численными расчетами, практически совпадают. Например, их максимальное различие, зафиксированное в расчетах в момент времени, при котором vd=0.999999 (значение, близкое к конечному vd=1) получилось следующим: 1) для е =10-2(v-(vvd)1/2) = = -0.016, w-еY3=0.19, v-(vd-w2/vd)=0.065; 2) для е =10-4( v-(vv d)1/2)=-0.0018, w - еY3=0.054, v-(vd-w2/vd) =0.0048. Видно, что с уменьшением е это различие становится все меньше, а самое большое при максимальном значении е = 10-2 не превосходит 20 %. Используя (8), для энергии частиц на втором этапе можно получить 1/Yd = VY2 - s2Y6, из чего следует, что при завершении процесса ускорения, т. е. при vd=1, энергия имеет предельное значение Ym=е-1/4. Это означает, что при конечных значениях е максимальная энергия частиц, полученная за все время ускорения, ограниченна, а ее предельное значение контролируется величиной ε. Зависимость предельной энергии Ym от е показана на рис. 2. Приведены две кривые, одна из которых получена с помощью численных расчетов, другая — это зависимость, представленная формулой Ym=е-1/4. Видно, что они мало отличаются друг от друга, что свидетельствует о безусловной надежности найденных приближенных решений (8). Оценим временной участок, на котором можно использовать формулы (8). Длительность этого участка можно определить из неравенства w/vd<1, которое можно представить в виде т>у3. На начальном участке ускорения, где vd=0, у ~ 1, это неравенство удовлетворяется при т>1, а в конце ускорения, где Ym=е-1/4, тт=1/е неравенство тоже справедливо, так как т = тт= 1/ s>Y3m = Vs3/4. Таким образом, можно считать, что запрещенный для использования формул (8) начальный отрезок времени тн пренебре- Рис. 2. Зависимость от параметра е предельной энергии Y™ полученной из численных расчетов (сплошная кривая) и по формуле Ym=е-1/4(штриховая кривая) жимо мал по сравнению с полным временем ускорения тт (тн~1<<тm= 1/е) и практически формулы (8) можно применять на всем временном участке ускорения частиц. В заключение этого раздела заметим, что, казалось бы, при vd ^1 можно воспользоваться решениями (5), (6), причем, чем ближе vd к единице, тем больше уверенность в справедливости этих формул. Однако выяснилось, что если 1-vd< е, остаточное время тост, в течение которого частица еще может ускоряться, слишком мало: тост<1. Это означает, что за такое время, как это следует из (6), нет заметного прироста энергии Ay, так как Ay< 1, и применение формул (5), (6) при благоприятном условии их использования (1-vd < е), к сожалению, оказывается бесполезным. РЕШЕНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ЧАСТИЦ МЕТОДОМ АЛЬФВЕНА НА ОСЦИЛЛЯТОРНОМ ЭТАПЕ На осцилляторном этапе, как следует из численных расчетов, динамика частиц определяется их дрейфовым движением в скрещенных электрическом и магнитном полях. Для решения задач с подобным поведением заряженных частиц Альфвен в свое время предложил метод, который можно считать уместным для использования в данном случае. Для поставленной задачи этот метод оказался весьма полезным. Метод Альфвена подробно описан в [Дорман и др., 1971]. Чтобы уверенно его применить, нам было необходимо выяснить значение е, при котором еще справедливо дрейфовое приближение, выполнение которого обязательно для метода Альфвена. В качестве предельного значения ε, для которого, как мы условимся, еще применим метод Альфвена, мы выбрали величину е=0.01 (при этом n = 16, т. е. поле Е достигает значения В за время, равное 16 циклотрон ным периодам). При более быстром нарастании Е, как мы полагаем, применение метода Альфвена для решения поставленной задачи уже вызывает сомнения. Следуя методу Альфвена, для решения уравнения движения в качестве первого шага представим скорость частицы как сумму двух скоростей — дрейфовой скорости vd = c[ЕВ]/В2 и скорости v1: v = vd+v1. Тогда уравнение движения примет вид dmvl = q[ v В]/c - m V. dt 1 dt В следующем приближении, принимая на втором шаге, что электрическое поле медленно нарастает во времени, учтем влияние малой силы d (m yvd) f =--—, действующей на частицу. Положим dt v1= v2 + vP, где vP=с[fB]/(qB2) — скорость дрейфа частицы под действием магнитного поля В и силы f. Учитывая, что векторы f и В взаимно перпендикулярны, в результате получим dmvll / = q[ v ,В]/c - dm' '. dt 2 dt (m / Vp ) На третьем шаге, положив — « 0, полу-dt чим решение уравнения движения в виде v=v2+vd+vP. Если ограничиться этим приближением, полученное решение будет характеризовать движение частицы по ларморовской окружности со скоростью v2 и ее дрейф в двух направлениях: электрический дрейф со скоростью vd в направлении, перпендикулярном электрическому и магнитному полям, и дрейф со скоростью vP в направлении вектора электрического поля E. Обратим внимание на то, что в линейно нарастающем электрическом поле на этом шаге решение v=v2+vd+vP, полученное нами методом Альфвена, для нерелятивистских частиц удовлетворяет уравнению их движения (про существование такого решения в нерелятивистском случае см. [Морозов, Соловьев, 1963]). Как видим, решение для компонент скорости v=ет, w=е (при v2 =0), полученное методом Альфвена и удовлетворяющее уравнению движения частиц, — это усредненное по времени точное решение (3). Из полученного нами приближенного решения следует, что за счет дрейфа частицы со скоростью vP будет происходить изменение полной энергии частицы ymc2, которое можно найти из соотношения mc2 — = qEv = qE с [fB]/(qB2) = dt Р = -mqcE d(Yvd) В /В2. Подставляя сюда v,=c[ЕВ]/В2, для векторного произведения d Cyvd)В dt получим d (Wd) В dt Следовательно, в нарастающем во времени электрическом поле прирост энергии определится из уравнения 2 (1-г2) dl ., dvL. dt dt В общем случае для рассматриваемого нами приближения vd<1 получим решение уравнения (9) –1/2 Y = (1-vd) . (10) В частном случае при vd<<1 решением уравнения (9) будет Y = exp ( vd2/2). (П) Таким образом, при малых vd <<1, согласно (11), полная энергия растет экспоненциально в зависимости от vd. При умеренных значениях vd, но при vd< 1 рост энергии определяется формулой (10), причем формально, как следует из (10), при vd→ 1 энергия γ неограниченно растет. При vd→0 (10) и (11) дают одинаковый результат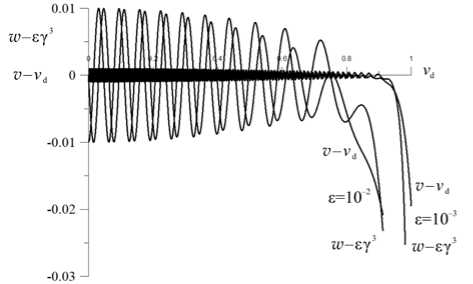
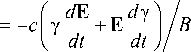
Список литературы Об ускорении частиц в постоянном магнитном поле и перпендикулярном ему электрическом поле, нарастающем во времени
- Альвен Х. Космическая плазма. М.: Мир, 1983. 216 с.
- Альвен Г., Фельтхаммар К.-Г. Космическая электродинамика. М.: Мир, 1967. 206 с.
- Дворников В.М., Кравцова М.В., Сдобнов В.Е. Диагностика лектромагнитных характеристик межпланетной среды по эффектам в космических лучах. Геомагнетизм и аэрономия. 2013. T. 53, № 4. C. 457-468. 10.7868/ S001679401304007X. DOI: 10.7868/S001679401304007X
- Дорман Л.И., Смирнов В.С., Тясто М.И. Космические лучи в магнитном поле Земли. М.: Наука, 1971. 399 с.
- Ландау Л.Д., Лифшиц Е.М. Теория поля. М.: Наука, 1967. 460 с.
- Морозов А.И., Соловьев Л.С. Движение заряженных частиц в электромагнитных полях. Вопросы теории плазмы. М.: Госатомиздат, 1963. Вып. 2. С. 177-255.
- Dvornikov V.M., Sdobnov V.E. Variations in the rigidity spectrum and anisotropy of cosmic rays at the period of Forbush effect on 12-15 July 1982. International J. Geomagnetism and Aeronomy. 2002. Vol. 3, no. 3. P. 217-228.
- Lindberg L. Plasma flow in a curved magnetic field. Astrophys. Space Sci. 1978. Vol. 55. P. 203-225. DOI: 10.1007/BF00642589
- Lindberg L., Kristoferson L. Reverse deflection and contraction of a plasma beam entering a curved magnetic field. Cosmic Electrodynamics. 1971. Vol. 2. P. 305-380.
- Parker E.N. Interplanetary Dynamical Processes. New York; London: Interscience Publ., 1963. 284 p.


