Об ускоренных методах поиска канонического тензорного разложения

Ускоренные методы Нестерова широко используются для получения более быстрой сходимости и достижения нижних оценок на классе выпуклых задач [8]. Недавние работы обобщают методы Нестерова для применения к задачам невыпуклой оптимизации [3,7] и задачам, которые не напрямую не решаются методами первого порядка, например такими, как Alternating Direction Method of Multipliers (ADMM) [4].

В данной работе нашей целью является обобщение ускоренных методов Нестерова на задачу альтернированных наименьших квадратов (ALS) для вычисления канонического тензорного разложения ранга г. А именно приближения исходного тензора суммой т тензоров ранга 1. В литературе описанная задача называется Canonical Polyadic (СР) decomposition of a tensor [6].

Представленный метод имеет теоретические гарантии сходимости для невыпуклых задач, какой и является задача канонического разложения, а также использует ускорения шагов альтернированной минимизации вместо традиционнных градиентных шагов, что является преимуществом данного метода. Но это же является и недостатком, так как при приближении к стационарной точке процедура линейного поиска становится нестабильной из-за нехватки машинной точности. Для разрешения этой проблемы предлагается рестар-товать метод при достижении нехватки точности.

Техника рестартов также рассматривалась в работах по ускорению методов решения нелинейных систем [9], выпуклых задач [4,10,11], а также нахождения неотрицательных матричных разложений [2].

Несмотря на отсутствие теоретических гарантий, в работе также проводится сравнение с ускоренным методом с адаптивным выбором весов. Метод не является монотонным и потому может не сходиться к стационарной точке, однако в среднем показывает хорошую сходимость.

Каноническое разложение позволяет представить каждый элемент тензора следующим способом:

Т

T_i3k = ^A_ipB₃ p C_kp.

p =i

На рис. 1 показано наглядное представление каконического разложения.

Более общим образом задачу можно сформулировать как задачу поиска приближенного канонического разложения, то есть поиска матриц A, B, C, которые минимизируют функцию f:

т тгзк - VA,pB3pCkp\ ^ r min        .           (1)

^                  AeRIxr ,BeRJxx,ceRKxx p=1          / где ж = (A, B, C)T.

Метод альтернированных наименьших квадратов находит каноническое разложение итеративным образом. На каждой итерации метод последовательно обновляет одну из матриц A, B или C, минимизируя (1) при фиксированных остальных матрицах.

Выпишем частные производные функции f [1]:

df _ 9A -T1 (B Ө C)+ A ((BTB) * (CTC)) , (2) df = dB -T2(A ӨC )+B {{ATA) * (CTC)) , (3) df = dC -T3(A ӨB)+C ((ATA) * (BTB)), (4) где Ө - произведение Хатри-Рао [1, 6], * - покомпонентное умножение, Т - матричная срезка тензора Т в направлении г [1,6].

bi                            Ьг

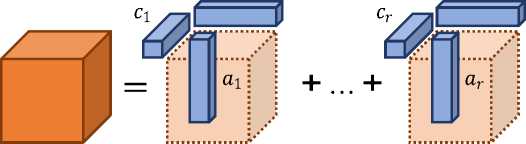
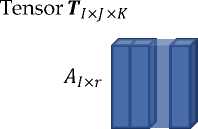
Рис. 1. Нахождение матриц А, В, С при заданыом тензоре T and СP-rank г

Формулы обновления матриц А, В, С выводятся путём приравнивания частных производных (2) - (4) к нулю и последующего решения системы линейных уравнений [1]:

ТДВ Ө С)= А ((ВтВ) * (СтС)) ,(5)

Т2(А Ө с) = В ((АтА) * (СтС)) ,(6)

Тз(А Ө В) = С ((АтА) * (ВтВ)) .(7)

На каждой итерации методом альтернированных наименьших квадратов решаются эти системы относительно матриц А, В и С и выписываются явные формулы решения для А, В и С при фиксированных двух других матрицах [1]. Алгоритм альтернированных наименьших квадратов (Algorithm 1) имеет следующий вид:

Algorithm 1 Alternating Least Squares for CP

Вход: Тензор T G R^{/xJ xK}. ранг pa::іложеішя г.

Выход: Матрицы А G R^/xr, В G R^{J xr} и С G R^{K xr}.

Инициализируем А, В, С.

for к <  N.

• 1.    А^к+1 = argmin2 ||T(i) — А(С^к Ө В^к)^т||р.

• 2.    В^{к +} = argmin 1 ||T₍₂₎— В(С^к Ө А^к)^т||^. в

• 3.    С^k+1 = argmin2 ||Т_№— С(В^к Ө А^к)^т|^,

3.    Ускоренный метод альтернативных направлений

А

где Т (г) - раскрытие (шгfolding) матрицы T по iiii дексу г.

В данном разделе разберем вариацию Алгоритма 2 для задач, допускающих альтернированную минимизацию. В работе [5] рассмотрена такая вариация для функций с лип-шицевым градиентом. Далее приводится модификация алгоритма для решения сильно выпуклых задач, допускающих альтернативную минимиизацию (Algorithm 2).

Для удобства введем обозначения. Множество {1,...,N} векторов {e^J^i ортонор-мированного базиса разделено на п непересекающихся блоков Д, к G {1,...,п}. Пусть

S k (ж) = ж + span{e« : г Е I k } - подпространство, содержащее ж, построенное на базисных векторах к-то блока.

Algorithm 2 Accelerated Alternating Minimization

Вход: Начальная точка жд.

Выход: ж^к.

Полагаем Ад = 0, ж ⁰ = ж ⁰.

for к >  0.

• 1.    Полагаем

• 2.    Полагаем y^k = ж^к + 3_к(ж^к — ж^к).

• 3.    Выбираем г_к = argmax_iG{i,...,_n}^Vi/ ⁽y^k )^|2-

• 4.    Полагаем ж^{k +1} = argmin_$G5.^ (^f (ж).

• 5.    Если L известно, находим Qk+i из уравнения (АД+ДТ) = тй- Если L не известно, находим Qk+i из уравнения

• 6.    Полагаем A k +1 = A k + Q k +1-

• 7.    Полагаем v^k+1 = argmin^_GRv-^_k+1(ж) .

3 k = arg;тіп_/3е[д,_1]/ ^^k + 3 (v^k — ж^к)}.                         (8)

a 2

О2,!

3 (У ) -       1      №f (y^k )|Ц = f(ж^{k +1} ).                     (9)

²(^A k ^{+ Q}k+i)

Адаптировав этот алгоритм к задаче канонического разложения, получим алгоритм с одномерным поиском следующего вида (Algorithm 3).

Algorithm 3 Accelerated ALS - Line Search (AALS - Line Search) / ^A0

Вход: Начальные точки ж⁰ = ж⁰ = I В д С д

Выход: ж^.

for к 6 N.

• 1.    Полагаем y^k = ж^k + 3 k (^yk — ж^k) , { Наилучшая выпуклая комбинация} ^гД^е 3_k = argmin f (,,ж^k + 3(v^k — ж^k)).

• 2.    Полагаем ж^k+1 = argmin f (ж ) ,{ Шаг альтернативной минимизации} €

• 3.    Полагаем -y^k+1 = v^k — Qk+iVf (y^k). { Евклидов проксимальный шаг}

^G[0,1]

где ^ = argmax |V₅f(y^k)|2- € G{ A,B,C }

Также сравним представленный алгоритм с адаптивным выбором весов, с которыми добавляется моментное слагаемое (Algorithm 4).

Algorithm 4 Accelerated ALS - Adaptive (AALS - Adaptive)

/ Ао

Вход: Начальные точки v⁰ = ж⁰ = I Во С о

Выход: x^N.

for k 6 N.

• 1.    Полагаем y^k = x^k + 3 k (v^k — $^k ) , где Дщ = 2^^ + ^ 4^ + «kirtl •

• 2.    Полагаем ж^¹ = argminf(ж ), { Шаг альтернативной минимизации} £

• 3.    Полагаем v^k+1 = v^k — « k +i Vf (y^k ). { Евклидов проксимальный шаг}

где £ = argmax ||V₅f (y^k )|2.

Е.е{ А,в,С }

Далее приводится алгоритм с рестартами (Algorithm 5). Критерием выхода из процедуры одномерного поиска является выполнение двух условий f (y^k) 6 f ^^k) и (Vf (y^k ),v^k — y^k ) > 0. Если процедура одномерного поиска достигает необходимости искать подходящую точку на отрезке длиной Ь і — « і > E_mac hi _ne, ^то следует рестартовать метод.

Algorithm 5 ALS - 5G

Вход: Starting point ж⁰.

Выход: y^N.

for k 6 N.

• 1.    while Ь_і — ^a i > ^E machine'

• 1)    Выполнять AALS - Line Search с начальной точкой жk и пол учить yk.

• 2.    Выполнить 1 итерацию ALS с начальной точкой yk и получить ж&.

4.    Эксперименты

Тензор T конструируется с помощью случайного выбора матриц А G R^ ^хт,В G R^ ^хтпС G R^^xr из (лапдартпого норм;гтыюго распределения N (0,1). Каждый столбец нормируется, и целевой тензор имеет вид

T = (А, В, С) • I + д М^ВСМдN, llN 11г где N - трехмерный тензор нормального шума, д - отношение сигнал-шум.

Генерация плохо обусловленного случайного тензора. Здесь каждая из матриц А, В, С генерируется с помощью сингулярного разложения. Диагональная матрица в разложении выбирается плохо обусловленной, например для матрицы А G R^^хг:

А = Ua^aVa, где Ua G R^хг и Va G Rrxr сгенерированы случайно с векторами-столбцами единичной длины, матрица У a G Rrxr диагональная, ее спектр разделен на 2 группы, в каждой группе элементы спектра распределены равномерно. Первая группа - на [IJK/2; I JK], вторая -на [0;1].

Для измерения качества используется стандартное относительное отклонение (RSE):

RSE =

Ц Т — TIf IITIf

Далее следует численное сравнение всех представленных алгоритмов.

Random 30 x 30 x 30 tensor with CP rank 20. 20 runs

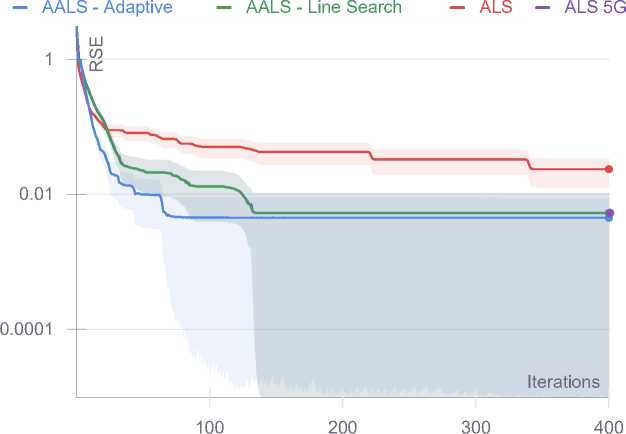
Random 30 х 30 х 30 tensor with СР rank 20. 20 runs

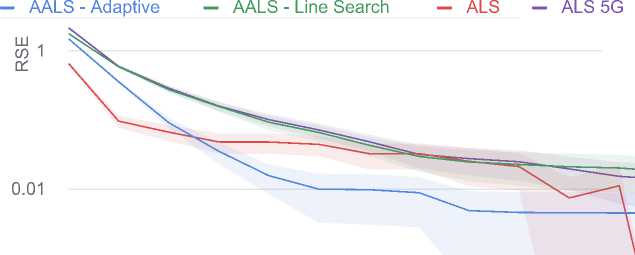
0.0001

Wall time

Random 30 х 30 х 30 tensor with СР rank 20. 20 runs. Grad norm

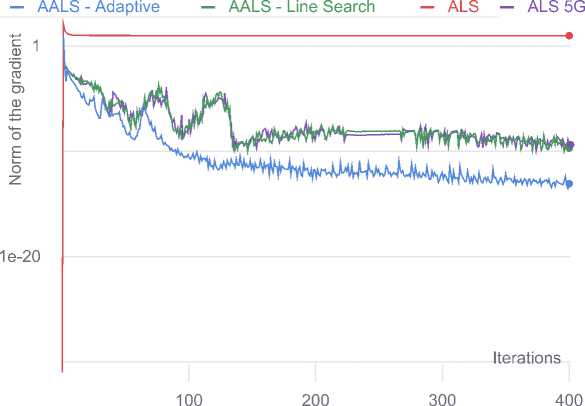
Ill-posed 30 x 30 x 30 tensor with CP rank 20. 20 runs

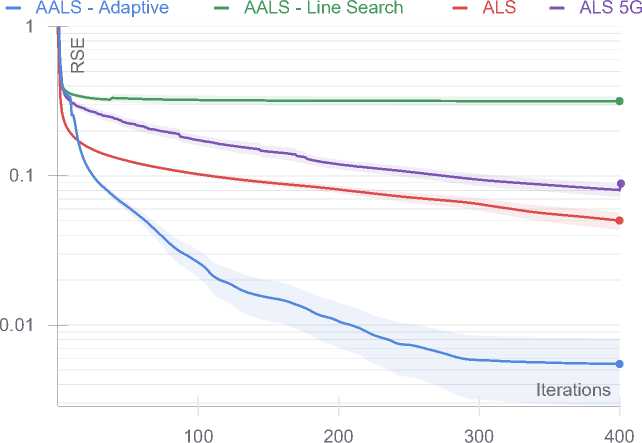
Ill-posed 30 x 30 x 30 tensor with CP rank 20. 20 runs

0.01

0.0001

Wall time

Ill-posed 30 x 30 x 30 tensor with CP rank 20. 20 runs. Grad norm

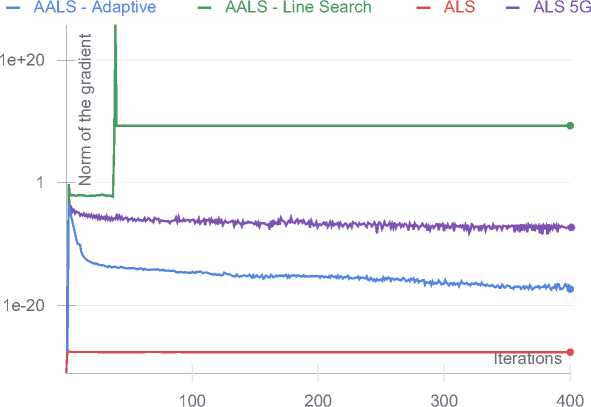
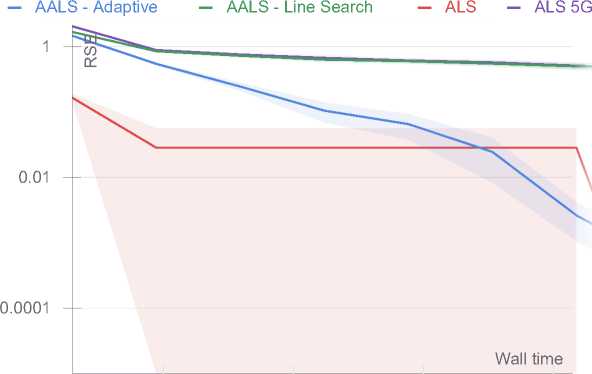
Random 100 x 100 x 100 tensor with CP rank 25. 5 runs

' AALS - Adaptive ^^е AALS - Line Search ALS ^^м ALS 5G

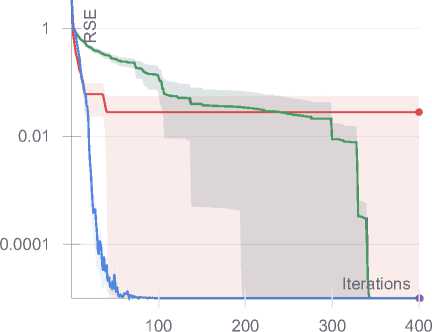
Random 100 x 100 x 100 tensor with CP rank 25. 5 runs

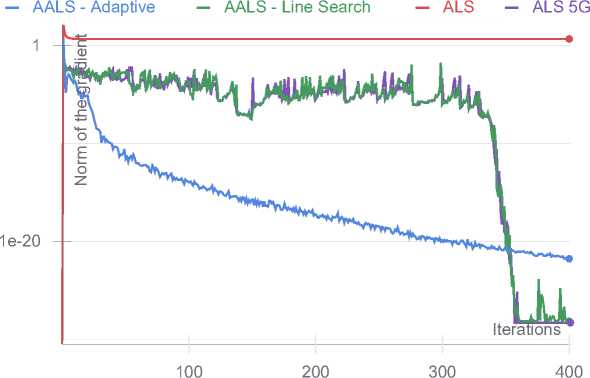
Random 100 x 100 x 100 tensor with CP rank 25. 5 runs. Grad norm

Ill-conditioned 100 x 100 x 100 tensor with CP rank 25. 3 runs

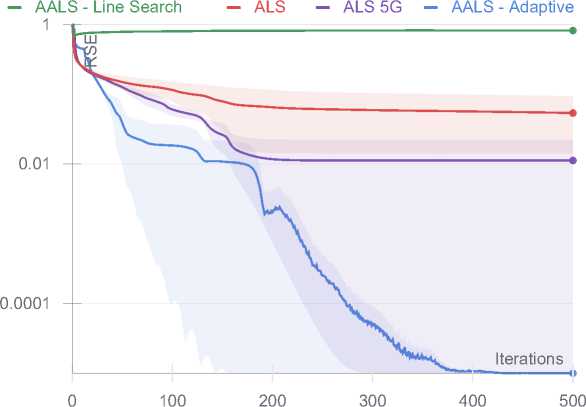
Ill-conditioned 100 x 100 x 100 tensor with CP rank 25. 3 runs

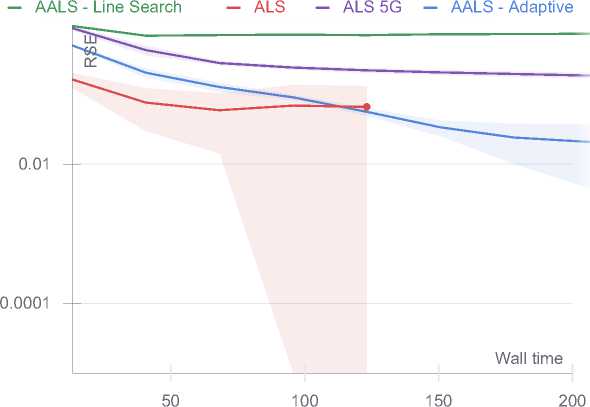
Ill-conditioned 100 x 100 x 100 tensor with CP rank 25. 3 runs. Grad norm

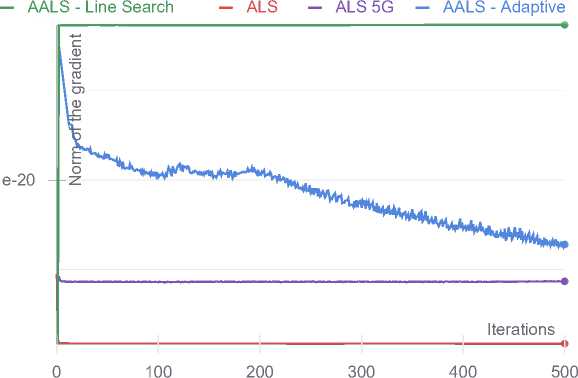
Рис. 2. Результаты численных экспериментов

5.    Заключение

Для тензоров малого размера наблюдается более быстрая сходиомсть адаптивного метода (Algorithm 4) для случайной и плохо обусловленной задачи. При этом, как было сказано выше, метод не имеет гарантии сходимости для данной задачи. Также следует отметить более быструю сходимость неускоренного метода альтернированных наименьших квадратов по сравнению с остальными методами по норме градиента для задачи малого разме ра (30 х 30 х 30).

Для задач большого размера (100x100x100) адаптивный метод также демонстрирует более быструю сходимость, но есть и исключения, где Algorithm 5 в среднем опережает остальные алгоритмы по итерациям.

Плохо обусловленные задачи большого размера иллюстрируют различное поведение представленных алгоритмов. Адаптивный алгоритм (Algorithm 4) показывает себя наилучшим образом.

Для более правильного сравнения следует решать задачу одномерного поиска явно, а именно находить более точно (или явно) корни полинома третьей степени. Возможно, метод с одномерным поиском проигрывает в некоторых эксперинтах именно по причине нехватки машинной точности. Следует более детально исследовать этот вопрос.

Исследование выполнено при поддержке Министерства науки и высшего образования Российской Федерации (госзадание) №075-00337-20-03, номер проекта 0714-2020-0005. Работа была выполнена в рамках проектной смены в Сириусе 2-23 августа 2020 г. (рук. А. С. Ненашев).