Об устойчивости колец, подкрепленных нитями одностороннего действия

Исследуется устойчивость упругих колец, подкрепленных нерастяжимыми нитями. В отличие от классического случая наличие односторонних связей приводит к определению параметров, при которых вариационная задача с ограничениями на искомые функции в виде неравенств имеет нетривиальное решение. В работе дано численное решение задачи устойчивости подкрепленных нитями колец, находящихся под действием центральных сил или внешнего нормального давления с применением сплайн-аппроксимации. Изучены два вида подкрепления: центральные нити и нити, расположенные по сторонам правильного m- угольника. Некоторые задачи устойчивости с неудерживающими связями рассматривались авторами в работах [1, 2].

1. Постановка задачи

Рассмотрим задачу устойчивости упругого кольца радиуса R, нагруженного внешним давлением P , и подкрепленного упругими нитями, которые не воспринимают сжимающих усилий. Пусть ϑ – цен- тральный угол, x(d) = R cos d, y(d) = R sin d - координаты точек кольца. Введем систему единичных ортов (i,j), орт j - единичный вектор касательной, орт i – единичный вектор, направленный в сторону внешней нормали. Рассматривается случай плоской деформации кольца, тогда вектор перемещений имеет вид

П = w (d) i + v (d) j, где w(d) - прогиб, v(d) - касательное перемещение.

Предположим, что кольцо подкреплено нитями одностороннего действия. Нити являются нерастяжимыми и не воспринимают сжимающих усилий.

Изучаются два вида подкрепления: в первом случае один конец нити прикреплен к неподвижному центру кольца, а другой – к некоторой его точке, d = d i - соответствующий угол, таким образом, что расстояние между центром кольца и точкой прикрепления нити не может увеличиваться. Это приводит к ограничениям на перемещения

w ( d j ) <  0 , j E M i = [1 ..m i ] , (1)

где m1 – количество таких нитей. Во втором случае один конец нити прикреплен к точке кольца, соответствующей углу d 1 = e 1 j , а второй - к углу d2 = е2j таким образом, что расстояние между точками прикрепления нити не может увеличиваться. Пусть aj = E 2 j — E1 j .

Обозначим p j = 2 R sin ^a 2 ^j - расстояние между точками прикрепления нитей до деформации. Пусть

Здесь S ⁽ r ) - производная порядка r .

Введем вектор z = (z 1, z2,.., Zn), zi = w($i), i E [0• •n].

Подставляя сплайн S ( w,$ ) в (5) , получаем две квадратичные формы

£ 1 = w ( E i j ) , £ 2 = w ( E 2 j ) , П 1 = V ( E 1 j ) , П 2 = V ( E 2 j ) •

Тогда расстояние между точками после деформации будет равно

f ( z ) = j /2 " ( s '' ² — 2 s ' ² + s ² ) d$ = ¹ ( Az, z ) (8) ² o                              ²

и

*

p j =

sin O i j + ^ 2 cos a j — n 2 sin a j — £ 1 ) 2 +

g ( z ) = j Г " ( s ' ^{2 2} Jo

-

bs ² ) d$ = ^( Qz,z )    (9)

a •                                            2

+ ( R cos °^A + £ 2 sin a j — n 2 cos a j — n 1 )²) . (2)

Таким образом, для этого подкрепления должно выполняться неравенство

ρj∗

-

P j <  0 , j E M 2 = [ m 1 + 1 ..m 2 ] .    (3)

Считая деформации малыми, можно приблизительно предположить

α j         α j α j α j

p * - P j = ^sin у ^£ 1 ^{— cos} у ^£ 2 ^+cos у n 1 + ^sin у n 2 .

Для j E M ₂ . Выражение (4) есть первый ненулевой член ряда Тейлора по переменным £ 1 , £ ₂ , n 1 , П 2 • Считая деформации кольца плоской, приходим к задаче : найти минимальное значение силы P, при которой вариационная проблема

(дифференцирование в (8) - (9) осуществляется по $.) Интегралы от сплайна S(w; $) и его производных вычисляются с помощью системы MAPLE 13. Используя условие несжимаемости (6), запишем v ($i ) = — / w ($) d$ = [ s (z,$) d$. oo

Для численного интегрирования по формуле трапеций находим

1i                             1i

^{v (} $ i ) = 2 5Z^{( w} j - 1 ^{+ w} j ) h = 2 ^ ^z j - 1 ^{+ z} j ) h j =1                      j =1

(10) причем, можно положить из условия периодичности V o = 0 , V n = V o .

J ^{( w} ) = 2 R / ^{( w} '' ^{+ w ) 2} d$^—

/ ( w ' ² — bw ² ) d$ ^ min ² Jo                       ^w

2. Решение задачи нелинейного программирования

Ограничения (1) , (3) , (4) образуют конус, определяемый линейными неравенствами

( a j ,z ) <  0 , j E M i U M 2 .

при ограничениях (1) - (3) имеет нетривиальное решение. В (5) b = 1 в случае сил внешнего нормального давления (нагрузка все время остается нормальной к деформированной оси кольца), и b = 2 в случае центральных сил (нагрузка до и после деформации направлена к неподвижному центру кольца). В (5) B - жесткость кольца при изгибе, первый интеграл представляет собой упругую энергию кольца, второй - работу внешних сил [1]. Прогиб w ( $ ) связан с касательным перемещением v ( $ ) условием несжимаемости

Если j E M 1 , то ограничения (11) записываются в виде z j <  0 . Если же j E M ₂ , то коэффициенты линейной формы (11) определяются следующим образом: ф ( z ) = p * — p j . Полагаем z k = 1 ,j ₀ E M ₂ , z j = 0 , при j = k. Тогда a _k = ф ( z ) — ф (0) . Обозначим через Г конус, определяемый неравенствами (11) , и рассмотрим задачу нелинейного программирования

f ( z ) =

2 ^ ^{( Az,z} ) ^ min ,

V = —w.

при ограничениях

Для конечномерной аппроксимации прогиб w ( $ ) будем приближать интерполяционными кубическими периодическими сплайнами

g ^{( z} ) =

2 £( Qz,z ) ^ min ,

( a j ,z ) <  0 , j E M i U M 2 .

S ( w, $ ) — w i (1 — t ) ² (1 + 2 1 ) + w i +i 1 ² (3 — 2 1 )+

+ m i ht (1 — t ) ² — w i +1 ht ² (1 — t ) ,

t = h 1($ — $i), t E [0; 1], h = $i+1 — $i = —, n n – число точек сетки. При этом должны быть выполнены условия периодичности

S ⁽ r ) ( w ; 0) = S ⁽ r ) ( w ;2 n ) , r = 0 , 1 , 2 .

Пусть z * - решение задачи (12) - (13) . Тогда по теореме Куна–Таккера найдутся множители Лагранжа А * и p j , j E M 1 U M ₂ , такие, что

Az * — A * Qz * +      ' p j a j = 0 .    (15)

j ∈ M 1 ∪ M 2

P j >  0 и выполнены условия дополняющей нежест-кости

P j ( a j , z * ) = 0 .

Умножая скалярно (15) на z * , находим f ( z * ) — X * g ( z * ) = 0 , ||z * П >  0 . Так как z * - решение (12) - (14) , то, очевидно, для всех X < X * квадратичная форма

2 ^ ⁽ Az, z ) ^—х 2 ^ ⁽ Qz, z ) > ⁰

для всех z Е Г, т.е. является условно положительно определенной на конусе Г. Таким образом, множитель Лагранжа λ∗ есть значение безразмерного па- раметра

PR ³

* B критической нагрузки. Задача (12)-(14) является задачей невыпуклого математического программирования. Для ее решения можно предложить метод последовательных приближений [1].

• 3.    Обсуждение результатов

Результаты вычислений представлены в таблицах 1,2. Для множества M 1 нити прикрепляются в вершинах правильного m–угольника, для множества M ₂ нити расположены по сторонам правильного m– угольника, как изображено на рисунке.

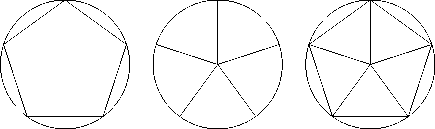
Рис. Способ подкрепления: при M 1 = 0 и M 2 = 0 (слева), при M 1 = 0 и M 2 = 0 (в центре), при M 1 U M 2 , M 1 = 0 и M 2 = 0 (справа).

Fig. The way of reinforcement: for M 1 = 0 and M ₂ = 0 (left), for M 1 = 0 and M ₂ = 0 (middle), for M 1 U M 2 , M 1 = 0 and M 2 = 0 (right).

Таблица 1

Случай центральной нагрузки

Table 1

The case of central load

m	5	7	10	14	20	25
M 2 = 0	7.73	10.84	13.16	15.34	17.99	18.71
M 1 = 0	4.92	9.12	13.89	17.98	32.98	43.41
M 1 ∪ M 2	7.73	12.30	20.31	32.65	53.24	84.96

В работе [2] получено точное значение безразмерного критического параметра в случае непрерывного распределения центральных нитей ( M 2 = 0 ) P * = 18 . 72 . Значение критической нагрузки для кольца без подкреплений P ^* = 4 . 5 .

Таблица 2 Случай нормальной нагрузки

Table 2 The case of normal load

m	5	7	10	14	20	25
M 2 = 0	4.90	5.63	7.19	7.20	7.73	8.001
M i = 0	3.18	7.20	10.07	14.76	31.03	41.06
M 1 ∪ M 2	5.41	9.21	17.59	29.30	48.40	79.58

В случае непрерывного распределения центральных нитей ( M 2 = 0 ) вдоль обода кольца точное значение критической нагрузки P * = 8 . 0 [1]. По результатам численных экспериментов при подкреплении кольца центральными нитями для m >  25 , нити можно считать непрерывно распределенными по ободу кольца. Значение критической нагрузки для кольца без подкреплений P * = 3 . 0 .

Таким образом, при малых m подкрепление нитями вдоль сторон правильного многоугольника слабо влияет на значение критической силы. При возрастании m значение критической нагрузки быстро растет.

Заключение

В работе показано, что значение критической силы значительно возрастает при подкреп- лении кольца нитями вдоль сторон правильного m-угольника. Особенно эффективным является комбинированное подкрепление (M1 ∪ M2). При большом количестве нитей подкрепления (m = 20), значение критической силы возрастает в почти в три раза в случае центральной нагрузки и почти в семь раз при нормальной нагрузке.

Работа выполнена при частичной финансовой поддержке Программы фундаментальных исследований УрО РАН, проект № 18-1-1-7.