Об устойчивости стационарной формы вращающейся кольцеобразной мембраны с регулярно прецессирующей центральной жесткой вставкой

В настоящее время при проектировании крупногабаритных космических аппаратов различного назначения с разворачиваемыми элементами конструкции мембранного типа можно выделить три основных концептуальных подхода: конструкции с мембранами, натянутыми на каркасы, бескаркасные мембранные конструкции с надувными полостями и бескаркасные конструкции с вращающимися мембранами, растянутыми центробежными силами инерции [1, 2, 3]. У последнего типа конструкций есть неоспоримое преимущество в том, что при прочих равных условиях отношение массы к площади развернутой поверхности мембраны минимально и может достигать 5 грамм на квадратный метр. Это позволяет в перспективе создавать аппараты с солнечными парусами, которые не будут требовать запаса реактивного топлива на борту для выполнения траекторных и угловых маневров, то есть все маневры могут осуществляться силами солнечного давления в сочетании с гравитационными маневрами. Благодаря относительной простоте и надежности механизма раскрытия центробежными силами инерции конструкции с вращающимися парусами были реализованы в японском проекте «IKAROS» [3] и эксперименте «Знамя-2» [1]. Несмотря на ряд преимуществ конструкций космических аппаратов с вращающимися солнечными парусами, их динамическое поведение при выполнении угловых маневров более сложно, в частности, из-за гироскопического момента, воздействующего на систему с распределенными параметрами. Тем не менее перечисленные выше достоинства таких аппаратов заставляют искать пути преодоления сложностей, возникающих при проектировании систем управления движением.

В работе аналитически исследуется напряженно-деформированное состояние вращающегося пленочного диска, находящегося под нагрузкой центробежной силы и гироскопического момента, возникающего при повороте оси вращения центральной вставки отражателя в процессе выполнения угловых маневров. Методом Ляпунова, примененным к системе с распределенными параметрами, доказывается устойчивость найденной формы, а также асимптотическая устойчивость в случае рассеяния энергии колебаний в соответствии с гипотезой Фойгта [4].

• II.    Стационарная форма паруса при регулярной прецессии

Рабочая поверхность солнечного паруса представляет собой в развернутом состоянии сплошной круглый пленочный диск радиусом R = 50 м, радиус центральной жесткой вставки a = 5 м, толщина пленки 1,2 • 10 ^-5 м и плотность материала р = 1,4 • 10 3 кг/м ³ . Диск вращается с угловой скоростью Q = 0,5 рад/с, вследствие чего материал паруса (полиамидная пленка) находится в напряженно-деформированном состоянии.

Пусть система координат Oxyz с осями Резаля (Ox совпадает с осью вращения центральной вставки паруса) медленно поворачивается с угловой скоростью ω, например, вокруг оси Oy. Тогда во вращающейся системе координат Ox ⁰ y ⁰ z ⁰ , жестко связанной с центральной вставкой, при этом оси Ox и Ox ⁰ совпадают, уравнение движения мембраны будет иметь вид [5]

д / dW \ д / а _ф dW \ _ д ² W ∂r ^{σ r r} ∂r ∂ϕ r ∂ϕ ^ρr ∂t ²

+ 2^шрг 2 cos(y + fit),

где W(r,^,t) — смещение элемента пленки в нормальном направлении к плоскости вращения паруса в зависимости от переменной r в радиальном направлении, ϕ — в тангенциальном направлении и времени t; σ _r и σ ϕ — радиальное и тангенциальное напряжения мембранного диска, найденные из решения плоской задачи упругости в [5]. При этом предполагалось, что касательное напряжение o r_v _ 0 [6].

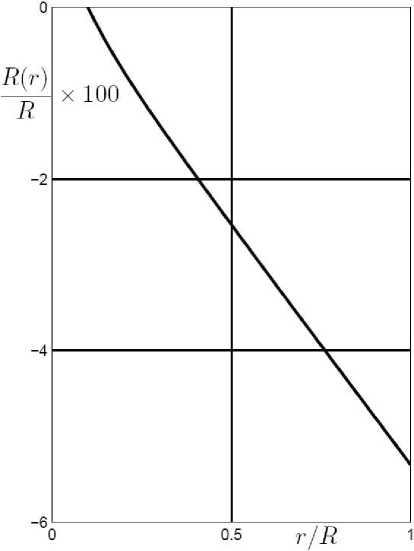
Рис. 1. Стационарная форма мембраны при регулярной прецессии. Радиальный профиль

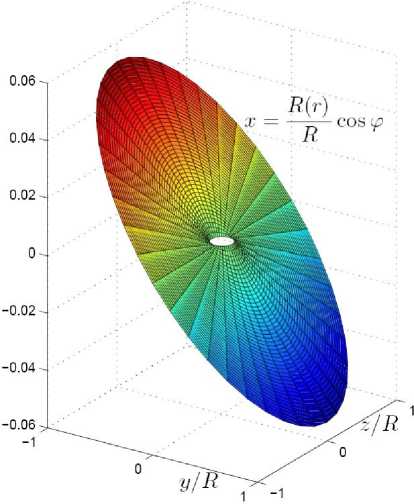
Рис. 2. Стационарная форма мембраны при регулярной прецессии. Пространственная форма

Неоднородная добавка в правой части уравнения (1) соответствует кориолисовым силам, возникающим при равномерной прецессии оси вращения паруса. Центробежными силами, возникающими из-за прецессии оси вращения солнечного паруса, пренебрегаем в силу малости угловой скорости ш. В статье [5] находится частное решение (1) вида W(r,^,t) _ R(r) cos(^ + fit), удовлетворяющее краевым условиям W|r=a _ 0 и orr dW |r^R- = 0 в радиальном направлении и W(r,^,t) _ W(r,^ + 2n,t) — в тангенциальном. Искомая функция R(r) записывается в конечном виде:

R ( r )

-

² П r

(3 + ^)A

(1 + A) ln

r ² - AR ²

a ² - AR ²

— In

r

a ²

,

где A _ — cR 4 , a 2 _ c ^ + 2 (R 2 - Za 2 ), c _ ^P K - (3 + ^), П _ 1+ ^ , Z _ 3+ ^ , ^ — коэффициент Пуассона.

Стационарная форма имеет вид

W стац (r,У,t) _ —

2шг

(3 + ^)Afi

(1 + A ) ln

r ² - AR ²

a ² - AR ²

-

In     cos(^ + fit)

a ²

в системе координат Ox ⁰ y ⁰ z ⁰ и

W стац (r,y) _

2шг

(3 + ^)Afi

(1 + A ) ln

r ² - AR ²

a ² - AR ²

-

in r 2 1 a ²

cos ^

в системе координат Oxyz (то есть не зависит от времени, что и объясняет название «стационарная»). Стационарная форма мембраны при регулярной прецессии в случае a/R = 0,1; y = 0,4; ш = 0,5236 • 10 ^-3 рад/с; Q = 0,5 рад/с представлена на рис. 1 и рис. 2.

• III.    Анализ устойчивости стационарной формы паруса при равномерной прецессии

  • III.1.    Прямой метод Ляпунова

Устойчивость полученной равновесной формы поверхности мембранного диска при равномерной прецессии оси его вращения доказывается прямым методом Ляпунова. Под устойчивостью стационарной формы (2) понимаем, что малые возмущения начальных условий стационарной формы приводят к малым отклонениям решения уравнения (1).

Необходимо отметить, что в данном случае метод Ляпунова применяется к системе с распределенными параметрами [7], описываемой уравнением движения (1). Поэтому в качестве аргументов функции Ляпунова выбираются поперечные мембранные усилия, которые являются линейными комбинациями от угловых перемещений ^∂ _∂ ^W _r и _r ^∂ _∂ ^W _ϕ и скорости поперечных перемещений ^∂ _∂ ^W _t . Эти переменные полностью описывают состояние любого элемента мембранного диска. Для каждого такого элемента можно построить положительно определенную квадратичную форму от перечисленных переменных и, проинтегрировав по всей поверхности мембраны, получить функцию Ляпунова в виде интеграла энергии:

V =

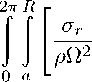
dW _ дW стац у + ^ / dW _ дW стац у   1

dr dr /   pQ ² Уду     rd у /    Q ²

∂W ∂t

∂W стац ∂t

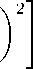
rdrdϕ,

где

дWстац _     2ш dr      QA(3 + y)

_   _z r2 _ AR ²       r ² r ² + R ² \

^{(1 +} A) ^ln( a ² - AR ² ) - ln a ^{2 + 2} Ar ² - AR ² ) ^{COs( y + Q t )} ,

дWстац =    2ш rdy    QA(3 + y)

(1 + A) ln(

r ² - AR ² a ² - AR ²

) - ln r ²

a ²

sin(y + Qt),

дWстац =  2шг dt     A(3 + y)

(1 + A) ln(

r ² - AR ² a ² - AR ²

) - ln r ² a ²

sin(y + Qt).

Функция Ляпунова принимает нулевое значение при подстановке в нее стационарной формы (2).

Покажем, что производная по времени ^d _d ^V _t , взятая в силу уравнения движения (1), равна нулю. Действительно,

2π R dV =2 Z Z ^r dt J J pQ2

0 a

dW +    ² f (1 + A) ln( ri - 4R 2 ) - ln r 2 +2 A ' R' у co*+Qt)

x

dr   QA(3 + y) V         a2 - AR2     a2     r2 - AR2/ x ■/' - „ 2   ' ((1 + A) h( / - AR) - ln r2 + 2A r2 + R2, У sin(p + Qt)l rdrd,+ drdt   A(3 + y) V         a2 - AR2      a2     r2 - AR2/           J

2 π R

+2 i! PQ 2

dW 2ш rdy  QA(3 + y)

(1 + A) ln(

r ² - AR ² a ² - AR ²

) - ln r2 У a2

sin(y + Qt)

x

d2W     2ш rdydt A(3 + y)

(1 + A) ln(

r ² - AR ² a ² - AR ²

) - ln r ² a ²

cos(y + Qt)

rdrdy+

_n Г f 1 FdW 2шг               _zr ² - AR²,   . r²\  . ,

⁺² J J Q ² [ dt   A(3 + y) (^{(1 + A ) ln(} a ² - AR ² )  ln a ² ) s* ^{+ Q t ) X}

0a д 2W   2“rQ dt2    A(3 + p)

(1 + A) ln(

r2 — AR2      r2 X a2 - AR2) - ln O2 J

cos(^ + Qt)

rdrdϕ.

Интегрируя по частям, принимая во внимание граничные условия W (a,^,t) = 0, W (r,^,t) — ограничено, обозначая для удобства S(r) = (1 + A) ln( у 2 AR ² ) — ln O ^ , получим:

2π R dV dt

dW 2“r

["aT — A ..SМ*1*   "

X

r ² + R ²

S(r) + 2A^---) cos(^ + Qt) + r2 — AR2

/   2 („) W +   2 ,„_)    2“

(pQ ² dr      rdr   pQ ² dr     QAr(3 + p)

O r д²W   O r    2“     / 2A r ² + R ²    4ArR ² (1 + A) X

⁺ pQ ² ar ^{2 +} pQ ² QA(3 + p) V r r ² — AR ² - (r ² — AR ² ) ² / ^{cos( y + Q t )+}

, ° ^ ^{д 2 W O} m ² “                        ^{1 a} 2 W ,

+Sb (r) cos(^ + Qt)             + pQ2 r2d^2   pQ2 QAr(3 + p)                  Q2 dt2

+—7727“---?S(r) cos(^ + Qt)^- cos(^ + Qt) +—^- cos(^ + Qt) >  rdrd^

AQ(3 + ^)                 Q              Q           J

Выделяя в фигурных скобках уравнение движения мембранного диска (1), подставляя выражения для σ ϕ , σ _r и A, получим

σ r ∂ ² W

X < ------—

(pQ ² ar ²

1d

pQ ² dr

(O r r)

+

σ _r

dV dt

—

2 π R

2 ZZ [ aW

0 a

d

pQ ² dr

∂W

^{( o} r ^{r )} rar

QAr(3 + p) (S ^{( r )+2} A

2       2A r ² + R ²

—

+

2“r

A(3 + ^)

S (r)sin(^ + Qt) x

σ ϕ ∂ ² W

pQ ² r ² d^ ²

r ² + R ²

r ²

—

pQ ² QA(3 + p) yr r ² — AR ²

и окончательно

dV dt

—

2 π R

■ i I

—

1 a ² W

Q ² at ²

o ^     2“

—

2“r      /    .        .

-Q- cos(^ + Qt) +

— AR² )  pQ ² QAr(3 + p)

S ^{( r ) +} WbS ^{( r )+}

—

∂W ∂t

4ArR ² (1 + A)

(r ² — AR ² ) ²

+—— cos(^ + Qt) I rdrdy

—

2“r

Ж+7)^{S < r )sin( v + Q t)}] ^X

σ ϕ

^XI VpQ ²

—

9   ot X    2“    / r2 + R2 X r2 +r^ ----:------- 2-:-------+ pQ2/ Qr(3 + p) \ r2 — AR2/

+

o r     2“

—

4rR ² (1 + A)

pQ ² Q(3 + ^) V (r ² — AR ² ) ²

+—— I cos(^ + Qt)rdrdy = 0.

Таким образом, устойчивость стационарной формы паруса при равномерной прецессии оси его вращения доказана.

• III.2.    Асимптотическая устойчивость

Применим гипотезу Фойгта [4], согласно которой напряжения σ _r и σ ϕ зависят не только от деформаций ε, но и от скорости деформаций ∂ ε/∂ t, то есть

σ _r

E

—

µ ²

E r + pE m + h-7— (fi r + pE m ) ∂t

E

—

µ ²

1+xl

∂t

(^E r ⁺ p^E m ),

E

" ^ф = I у ²

Е ф + ^E r + hdt (Е ф + ^E r )

E

1 — у ²

(1 + ^

∂t

(^Е ф + ^^E r ),

где h — коэффициент трения, E — модель Юнга, µ — коэффициент Пуассона.

В этом случае уравнение для нахождения стационарной формы выглядит следующим обра- зом:

f i +hd ) [ I" f "rdW ) + /Т (~dW )1 = pr^W +2fi^ ² cos(y+ ^Q t).

у dt J [dr у dr J dy yr dy / J       dt ²

Находим решение уравнения (3) методом Фурье в виде ряда

W(r,y,t) = X f q k ^{( t )} R 7 k= k =0 V     Vlk ⁿ

cos у + S k (t)

R k (r)

—n= ^sin У , l k π

где д! cos у и д! sin у — найденные в [5] собственные функции для однородной части уравнения (1) с собственными значениями ш 2 (здесь Л— — нормировочные коэффициенты).

k             l k π

Подставляя это представление в уравнение (3), имеем

∞

^— Pr X ^ 2

k =0

(q k (t) + hq k (t))

R k (r)

l k π

cos у + (S k (t) + hS k (t))

R k (r) l k π

sin у

∞

= PrX (^ k ^{( t )}

k =0

R k (r)

l k π

cos у + S k (t)

R k (r)

l k π

sin у

+

+pr • 2fiw

∞

X k=0

α k

R k (r)

l k π

cos у cos

∞

fit — £

α k

R k (r)

k =0

l k π

sin у sin fit

Сравнивая коэффициенты при собственных функциях, получаем уравнения для нахождения q k (t) и S k (t):

Г q k (t) + hw k q k (t) + W 2 q k (t) + 2fiwa k cos fit = 0,                          (.)

[ S k (t) + hw k S k (t) + ^ 2 s k (t) — 2fiwa k sin fit = 0,                              ²

где a k — коэффициенты разложения функций r cos у и r sin у по системам { RVr ) cos у } и {

Rk ( r )

k— sin у }.

l k π

Вводя новую переменную tk(t) = —qk(t) + iSk(t), перейдем от двух уравнений (4) к одному комплексному уравнению tk(t)+ hwktk(t) + w2tk(t) = 2fi^akeiQt. Решение в терминах этой переменной записывается как

W (r,y,t) = — Re XX t k (t)e i^ R ^ k^ r) k =0       vl k ⁿ

Находим частное решение последнего уравнения в виде t 4^aCTH (t) = Ckе^гт :

— C k fi ² e ^{i Q t} + ifiC k h^ 2 e ^{i Q t} + C k u 2 e i ^Ut — 2fiwa k e i ^nt = 0,

_ 2fi^ak k   ш2 — fi2 + ih^2fi

Следовательно, искомое частное решение будет иметь вид или

^W 4acTH (^ri^y,t)

∞

= —Re X k=0

R k (r)      2fi^a k

V l k n w 2

— fi ² + ihw k fi

e i ( ^ +Q t )

∞

W4acTH(riy,t) —  2fiW k=0

a k             R k (r)

(^ k — fi ² ) ² + (^_lш k. _fi) ^k Viks

cos(y + fit — Ay k ),

где A^ k = arg(w 2 — Q ² + ihw 2 Q) = arctan hi' kep •

ω _k - Ω

При h = 0, то есть в отсутствие демпфирования, видно, что W _4aCTH (r,^,t) совпадает с аналитическим решением (2), если разложить его в ряд по функциям Хейна.

При переходе в систему осей Резаля полученная форма принимает вид

∞

W Hac^ Cr,^) —  2 ^Q W   '

k =0

a k             R k (r)

^(_Ш к — Q ² ) ² + (h^ 2 Q) ² Vl k ⁿ

cos(^ — A^ k )

и не зависит от времени.

Общее решение уравнения (3) будет иметь вид

W (r,^^t = W общ . одн . (r,^,t) + W h3Cth (r,^,t) =

= X^ R k (r) k =0 √ l ^k π

hω _k ²

2 t ((A k cos W k t + B k sin W k t) cos ^ + (C k cos W k t + D k sin W k t) sin ^) +

⁺ W 4acTH ^{( r,}y^{,t )} ,

где W k = W k

V1

-

¹ ₄ h ² ω _k ² — частота собственных колебаний системы с затуханием.

Из (5) видно, что общее решение асимптотически стремится к W _4aCTH (r,^,t) — стационарной

форме. Таким образом, асимптотическая устойчивость доказана.

• IV.    Заключение