Об устойчивости упругих систем с неудерживающими связями

Решение классических задач на устойчивость упругих систем сводится к проблеме на собственные значения линейных операторов. В данной работе исследуется влияние односторонних ограничений на перемещения. В отличие от классического случая, наличие неудерживающих связей приводит к необходимости находить ”точки бифуркации” решений вариационных задач, содержащих ограничения в виде неравенств. Подробно рассматриваются задачи устойчивости прямоугольных пластин и торообразной оболочки при односторонних ограничениях на перемещения. Для конечномерной аппроксимации используются кубические сплайны. В первой части работы решается задача устойчивости прямоугольной пластины, прогиб которой ограничен двумя жесткими ребрами так, что контакт между пластиной и ребрами является односторонним, при этом на двух кромках пластины выполняются граничные условия свободного края. Во второй части рассматривается осесимметричная задача устойчивости торообразной оболочки вращения с упругим наполнителем внутри, находящейся под действием внешнего нормального давления. Для вычисления работы внешних сил используется точная термодинамическая формула. Исследуется влияние нелинейных слагаемых, обусловленных односторонним контактом с упругим наполнителем, на величину критической силы.

2.1. Постановка задачи

Пусть прямоугольная пластина нагружена по краям x = 0 , x = a ; 0 < y < b нормальными усилиями ст . Обозначим через w ( x,y ) , 0 < x < a, 0 < y < b прогиб пластины. Потенциальная энергия деформации пластины имеет вид [3]:

U ( w )

где

— / / (( Aw ) ² - (1 - v ) L ( w,w )) dxdy, ² 00 0o

∂2w ∂2w w = dx2 + dy2 ’

∂ ² w

L ⁽ w’w ) = 4 d. ■

∂ ² w

∂y ²

/ d ² w ) 2 ) ∂x∂y

Работа внешних сил может быть вычислена по формуле [3]

V ( w ) =

1 А 'KA

Задача об устойчивости пластины сводится к отысканию сил σ таких, что вариационная проблема

U — V ^ min

w

имеет нетривиальное решение.

Предположим теперь, что прогиб пластины может быть ограничен жесткими препятствиями так, что f w(x,y 1) < о,

\ w(x,y2) > 0, при x E [0, a при x E [0, a

где y 1 , y ₂ - фиксированные переменные из (0 , b ) . Функцию w будем аппроксимировать сплайнами [7]

n +2 m +2

w ( x,y ) = 52 52 W ij B i ( x ) B j ( У ) ,     (5)

i =0 j =0

где x E [0,l] , l = a, h = —, xi = ih,

B i ( x ) = B ( x — ( i — 3) h ) , i = 3 ..n — 1 ,

^{B ( x} ) = 4 h 4 (6 ^x + ^— 3 ^{( x} - h ) + ^{+ ( x} - ² h ) + ^—

• -    |( x - ³ h ) + ■ ^ x - ⁴ h ) + ) ,

^B 0 ⁽ x ) = ¹ + h 3 ( ^— 6 x + + 2 ^{( x} - ^h ) + ^—

• ^—    2 ^{( x} - ² h ) + ⁺ 6 ^{( x} - ³ h ) + ) ,

B i( x ) = x + h12 ( — j x + + 6(x - h)+ —(6)

• —    о (x - 2h)3 + +7 (x - 3h)3 ), 3        +    6

• B ₂ ( x ) = ^ x ² + — ( — — x ³ + - ( x — h ) 3 —

2( )    2 hV 36 + 2 ()

• ^— 4 ^{( x — 2 h} ) + ⁺ 18 ^{( x — 3 h} ) + ) ,

B n ( x ) = B 2 ( l — x ) , B n +1 ( x ) = B 1 ( l — x ) , B n +2 ( x ) = B 0 ( l — x ) , x + = max { 0 , x} = |( |x| + x ) .

Меняя в определении сплайнов x на y , n на m и полагая l = b , получим B j ( y ) . Подставляя (5) в (1) и (2) получим две квадратичные формы соответственно

^{f (} w ij ) = DD ЕЕ q ijks w ij w ks ^, ( ⁷ ) i,j ks

g ⁽ w ij )=2 ЕЕ r ijks w ij w ks ^. (8) i,j ks

Квадратичная функция f (wij) аппроксимирует упругую энергию пластины, g(wij) - работу внешних сил. Коэффициенты qijks, rijks есть интегралы по площади пластины от произведений Bi и их производных, в частности a′          ′                b rijks = J^ Bi (x)Bk(x)dx У0 Bj (y)Bs (y)dy.

Все эти интегралы могут быть вычислены аналитически с использованием системы MAPLE. Обозначим через f ( w ij ) = 1 /Df ( w ij ) и g ( w ij ) = 1 /ag ( w ij ) .

Если положить w0,j = 0, w2,j = 0, Wn,j = 0, Wn+2,j = 0, j E [1 : m], то при x = 0, x = a будут выполнены граничные условия шарнирного опирания:

w (0 , y ) = w ( a, y ) = 0 ,

( w xx (0 ,y ) = w xx ( a,y ) = 0 ,

Если же положить

0 < y < b.

w 0 ,j = 0 , w 1 ,j = 0 , w n +1 ,j = 0 , w n +2 ,j = 0 , j E [1 : m ] , то при x = 0 , x = a будут выполнены граничные условия жесткой заделки:

w (0 , y ) = w ( a, y ) = 0 , w x (0 , y ) = w x ( a, y ) = 0 ,

(10) 0 < y < b.

Будем предполагать, что при y = 0 , b выполнены граничные условия свободного края:

I

д2w(x,y) 1 ,,d2w(x,y) _ n dx2   + V dy2   = 0, д3 w(x,y) 1 — _ д д3 w(x,y)

∂x ³                ∂x∂y ²

= 0 , 0 < x < a.

Специально этим условиям удовлетворять не надо, так как коэффициенты wi,0, wi, 1, wi,2, wi,m+2, wi,m, wi,m+1 находятся в результате решения задачи оптимизации. Граничные условия (11) являются “неудобными“ в вычислительном отношении, так как они содержат производные третьего порядка.

Потребуем выполнение неравенств (4) в конечном числе точек:

^{w (} x j ,y 1 ) <  ⁰ , ^{—w (} x j ,y 2 ) <  ⁰ , x 1 = 4 a, x 2 = 2 a, x 3 = 4 a, y 1 = 3 b, y 2 = 3 b.

Подставляя (5) в (12) получим систему линейных неравенств, которым должны удовлетворять коэффициенты wij . Запишем эти неравенства в виде bijkwij < 0.

k =1

Обозначим через Г конус, определяемый неравенствами (13) . Таким образом, вместо (3) - (4) получаем задачу отыскания минимального числа λ ^∗ такого, что задача нелинейного программирования

f(wij) — X*g(wij) ^ min (14) wij EГ имеет нетривиальное решение. Она сводится к проблеме идентификации условной положительной определенности квадратичных форм на конусах.

• 2.2.    Об условной положительной определенности квадратичных форм на конусах

Рассмотрим задачу нелинейного программирования f (u) = -(Au,u) ^ min         (15)

2           uERn при ограничениях

g ( u ) =

|( Qu,u ) = 1 ,

( b j ,u ) <  0 , j G I = 1 : m. (17) Здесь A – положительно определенная, Q – неотрицательно определенная квадратные матрицы порядка n , b j G R n . Пусть u * - решение задачи (15) (17) . По теореме Куна-Таккера найдутся множители Лагранжа V j >  0 , j G 1 : m и А * такие, что

• ( Au * - A * Qu * + £ m =1 v j b j = 0 ,

• < g ( u * ) = 1 ,                                     (18)

• [ V j ( b j ,u * ) = 0 .

Определение 1. Точки u * , удовлетворяющие (18) , будем называть стационарными.

Введем обозначение B(А) = A - AQ. Можно показать, что для любых А < А* (B(А)u, u) > 0, для всех u G Г, и, напротив, если А > А*, то найдется вектор u G Г такой, что (B(А)u, u) < 0. Очевидно также, что А* = f (u*). Таким образом, матрица B(А) при λ ≤ λ∗ будет условно положительно определенной на конусе Г. Вопросы идентификации условной положительной определенности квадратичных форм на конусах рассматривались в работах [8], [9]. Там получены критерии условной положительной определенности квадратичных форм в важном частном случае, когда Г = {u G Rn luj > 0,  j G 1 : n}. Их применение сводится к вычислению большого количества определителей (в общем случае 2n), и в этом отношении является крайне неэкономичным.

Сформулируем метод последовательных приближений для поиска стационарных точек. Пусть решение u 0 G Г , g ( u 0 ) = 1 некоторое начальное приближение. Пусть уже получена точка u k ∈ Г , g ( u k ) = 1 . Обозначим

Гk = {u G Г, | (Quk ,u - uk) = 0}.(19)

Найдем точку u _k G Г _k такую, что

• |(Auk,uk) = min |(Au,u).(20)

• ²               uE Г k ²

Далее полагаем

• uk+1   sk uk, где sk   V^g^uky.

Поскольку e _k - решение задачи минимизации (20) , то найдутся множители Лагранжа v kj >  0 и A _k такие, что

^Au k ^A k ^Qu k ⁺ ^£ j = 1 ^ kj b j = ^{0 ,}

( Qu k , e k - u k ) = 0 ,                        ⁽²²⁾

• ^kj⁽bj ,^u )    ⁰.

2.3.    Обсуждение результатов

Можно показать, что последовательность {λ k } монотонно убывает, ограничена снизу, и любая предельная точка последовательности {u k } является стационарной. Обозначим предел последовательности {λ k } через λ ∗ .

Замечание 1 . Предлагаемый метод является локальным, и он сходится к решению задачи (15) (17) , если удачно выбрано начальное приближение. После того, как получено λ ∗ , можно воспользоваться методом ветвей и границ [10] для проверки условной неотрицательной определенности матрицы A - λ _∗ Q на конусе Г . Обычно в реальных задачах матрица

A-λ ∗ Q имеет небольшое число отрицательных собственных чисел, а трудоемкость метода ветвей и границ в задачах невыпуклого квадратичного программирования оценивается числом отрицательных собственных чисел матрицы. Если же применять метод ветвей и границ непосредственно к задаче (15) - (17) , то объем вычислительной работы будет зависеть от размерности пространства переменных.

Замечание 2 . На каждом шаге предлагаемого алгоритма требуется решать задачу минимизации выпуклой квадратичной функции при линейных ограничениях (задачу выпуклого квадратичного программирования). Последняя значительно проще исходной.

Замечание 3 . Если I = 0, т.е. Г = R n и Q -eдиничная матрица, то предлагаемый алгоритм превращается в известный метод Келлога для поиска минимального собственного числа матрицы A.

В табл. 1 приведены результаты вычислений значения критического параметра ст * = D ^{- 1} ст при a = 1 для различных видов граничных условий: I -граничные условия шарнирного опирания (10) , II -смешанные граничные условия, когда на левом крае x = 0 выполнены условия (9) , на правом - условия жесткой заделки (10) , III - граничные условия жесткой заделки (10) , IV - при x = 0 , a , 0 < y < b - граничные условия шарнирного опирания и при 0 < x < a , y = 0 , b граничные условия свободного края. В двух последних строках таблицы представлены значения σ ^∗ без ограничений на перемещения, вычисленные теоретически (предпоследняя строка) и методом, рассмотренным в п.2.2. (последняя строка).

Таблица 1

Значения критической силы σ ^∗ при различных граничных условиях

Гран.усл.	I	II	III	IV
b = 1	21.95	32.21	51.49	8.98
b = 0 . 5	60.40	69.44	91.85	5.37
Теор.	π 2 ≈ » 9 . 87	2 п 2 « « 19 . 74	4 п2 to to 39 . 48	п 2 / 4 to to 2 . 47
Прибл.	9 . 98	20 . 24	39 . 98	2 . 44

Из сравнения результатов 4 и 5 строки таблицы можно сделать вывод, что редукция вариационной задачи к задаче квадратичного программирования при помощи сплайнов является адекватной и достаточно точной. Так как при отсутствии ограничений на перемещения при граничных условиях свободного края при y = 0, b решение задачи w(x,y) не зависит от y (см. рисунок справа), то точные значения критических сил совпадают с эйлеровыми силами для стержней [3], и не зависят от b. При наличии односторонних ограничений на перемещения значения критических сил зависят от b. Влияние односторонних связей на перемещения (неравенства (4)) значительно повышает критическую нагрузку и может быть использовано для повышения несущей способности сжимаемых по кромкам пластин. Численные эксперименты показали, что выполнение ограничений (12) в нашем случае гарантируют выполнение неравенств (4). Различие в формах равновесия при наличии и отсут- ствии ограничений на перемещения проиллюстрировано на рисунке.

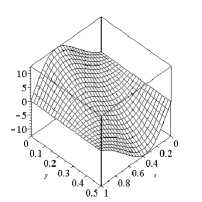
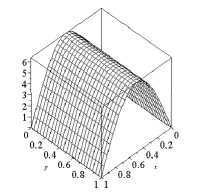
Рис. Форма равновесия пластины после потери устойчивости при наличии односторонних ограничений на перемещения (слева) и без ограничений на перемещения (справа).

• 3. Устойчивость торообразной оболочки при одностороннем подкреплении

3.1.    Определение упругой энергии и работы внешних сил

Предположим, что оболочка, срединную поверхность которой обозначим через S , в результате деформации приобрела форму S . Обозначим через g ij , h ij , g ij , h ij , i,j = 1 , 2 коэффициенты первой и второй квадратичных форм недеформирован-ной и деформированной поверхности соответственно. Предполагается, что деформация является осесимметричной. Согласно [2] энергию деформации, связанную с переходом из состояния S в состояние S , можно вычислить по формуле:

U =

11 Ф 1 ( e i ,e 2 ,k i ,k 2 ) ds,

где ф1 = 24(1 - v2) (K1 + K2 + 2VK1K2) +

Eh _{2   2}

⁺ 2(1 _{- V} 2 ) ^{( e} 1 ^{+ e} 2 ^{+ 2 Ve} 1 ^e 2 ) ’

E – модуль Юнга, ν – коэффициент Пуассона, ε 1 и ε 2 – экстремальные значения отношения

^{E 2} j =1 ⁽ g ij ^— g ij ) du i du j

^E ij =1 g ij du i du j

κ ₁ и κ ₂ – экстремальные значения отношения

^E 2 ,j =1 ( h ij - h ij ) du i du j

^E 2 ,₃ =1 g ij du i du j

В результате осесимметричной деформации поверхность S представляет собой поверхность вращения вокруг оси z некоторой кривой γ , расположенной в плоскости XOZ и задаваемой уравнениями x = ф ( 9 ) , z = ф ( 9 ) . Точка ( ф ( 9 ) , 0, ф ( 9 ) ) кривой y при повороте на угол А переходит в точку ( ф ( 9 ) cos А , Ф ( 9 ) sin А , ф ( 9 ) ), тогда уравнения поверхности вращения будут иметь вид [1]

{ х = ф ( 9 ) cos А, у = ф ^{( 9 )sin А},               (26)

z = ^{ф (} 9 1 .

Рассмотрим задачу устойчивости тора, нагруженного внешним нормальным давлением. Тогда в (24) и (25) и 1 = 9 - полярный угол в плоскости меридиана, и ₂ = А - угол в плоскости параллельного круга. Обозначим через w ( 9 ) и и ( 9 ) нормальное и касательное перемещения точек поверхности тора. Декартовы координаты точек торообразной поверхности до деформации будут определяться уравнениями

{ х = ( R + a cos 9 ) cos А, у =( R + a cos 9 )sin А,                 (27)

z = a sin 9, 0 6 9 6 2n, 0 6 А 6 2 n, т.е. для недеформированного тора ф = R + a cos 9, ф = a sin 9. После деформации уравнения поверхности будут иметь вид (26), где

Г ф ( 9 ) = R +( a + w ( 9 ))cos 9 — и ( 9 )sin 9,

|^ ф ( 9 ) = ( a + w ( 9 ))sin 9 — и ( 9 ) cos9.        ⁽⁾

Будем исследовать потерю устойчивости в малом по осесимметричной форме, когда образующиеся выпучины имеют вид кольцевых складок в направлении координаты λ (перемещения не зависят от λ ). Для поверхности вращения первая и вторая квадратичная формы поверхности записываются в виде [1]

I = ( y ² + ф ' ²) d9 ² + ф ² dА ² ,

II = ^Eф -^ ' ^ф ' d9 2 + ^{ф ф} dА ² . φ ^{′ 2} + ψ ^{′ 2}               φ ^{′ 2} + ψ ^{′ 2}

Для недеформированной поверхности:

{ 1 0 = a ² d9 ² + ( R + a cos 9 ) ² dА ² ,         (30)

[ II 0 = ad9 ² + cos 9 ( R + a cos 9 ) dА ² .

Используя формулы (24), (25), (27), (29), (30), можно получить выражения для деформаций ε1, ε2 и кривизн κ1, κ2. Квадратичные формы I и II в случае осесимметричной деформации имеют диагональный вид. Поэтому ф 2 + ф‘2 — a2

e 1                 2          , a2

ф ² — ( R + a cos 9 ) ²

e ²        ( R + a cos 9 ) ² ’

^< ф ф — ф ф 1

К1 = a 2^ ф'2 + ф'2 — a, ф ф — cos 9 (R + a cos 9) Jф 2 + ф'2

К 2 = ----------------------/         —.

cos ² 9 ( R + a cos 9 ) ² фф ² + ф' ²

Для внешнего нормального давления в соответствии с теоремой Эйлера-Бернулли работа внешних сил равна

A = P A V, где AV - изменение объема оболочки в результате деформации. Как известно [6], объем тела, поверхность которого задается уравнениями х = х(9, А), у = у(9, А), z = z(9, А), определяется (с точностью до знака) интегралом

V =

1 /2 ’ Г’ det

3 Jo  Jo

x ^{x ′} ′ ^θ x _λ

y

′ ^y θ ′ y _λ

z

′ z^

z _λ

dθdλ. (32)

В случае осесимметричной деформации определитель в (32) не зависит от X . Используя формулы (26) - (28) объем оболочки после деформации можно вычислить по формуле:

V =

2 п Г^{2 п}    /       ‘ д

— у Ф2 ^ w,u,w ,u ) de,

U 0 = u +2, U I = -U n +1 , U 2 = U n .

Введем вектор z ∈ R ^{2 n} с компонентами:

z 1 = w 0 , Z 2 = w 1 , ..., Z n = w n- 1 ,

Z n +1 = u 0 , Z n +2 = U 1 , ..., Z 2 n = U n- 1 .     (37)

Подставляя (36) в функционалы J1, J2, J3, получим соответственно функции f1(z), f2(z), f3(z) и f (z; P ) = f1 (z) + f2( z) — Pf3 (z).

Необходимое условие экстремума записывается в

где

Ф 2 = det Haj || ,i,j E 1:3 , элементы матрицы ∥ a ij ∥ имеют вид

виде

df ( z,P ) ₌ dz .

a 11 = r + a cos e + w (e) cos e — u (e) sin e, a 13 = a sin e + w (e) sin e + u (e) cos e, a21 = —a sin e + w (e) cos e — w(e) sin e—

— u (e) sin e — u (e) cos e, a23 = a cos e + w (e) sin e + w (e) cos e+

+ u (e) cos e — u (e) sin e, a32 = R + a cos e + w (e) cos e — u (e) sin e, a 12 = 0, a 22 = 0, a 31 = 0, a 33 = 0.

Предположим, что внутри оболочки находится упругий наполнитель, который работает как простое винклеровское основание с жесткостью C . Тогда полная энергия деформации будет иметь вид

J = J 1 ⁺ J 2 ^{— PJ} 3 ,

Для решения задачи устойчивости оболочки требуется найти минимальное значение силы P, при котором происходит бифуркация решения системы уравнений (38) . Необходимое условие бифуркации заключается в том, что матрица вторых частных производных становится вырожденной, т.е.

det

" д ² f ( z,P ) ■ ∂z ²

= 0 .

где

J 1 = 2 п

/  Ф 1 ( e

1 ,e ₂ , к 1 , к ₂ ) a ( R + a cos e ) de,

Введем в рассмотрение матрицы

_ д ² f 1 (0)           д ² f 2 (0)         д ² f 3 (0)

Q 1        9 , Q 2        9 , G <19

∂z ²              ∂z ²             ∂z ²

.

Тогда уравнение (39) означает, что система уравнений

Q 1 z + Q 2 z = ^Gz           (40)

имеет нетривиальное решение, где ц = P - обобщенное собственное число. Отметим, что f2(z) = 2 (Q2z,z) .

J 2 = 2 п

2 π

C 2 2 w

a ( R + a cos e ) de,

J 3 = A V.

В устойчивом положении равновесия полная энергия принимает минимальное значение. Таким образом, приходим к вариационной задаче

J ^ min , w,u

Задача поиска обобщенного собственного числа для системы (40) может быть сформулирована в виде экстремальной проблемы

X ( z ) = |( Q 1 z,z ) + 2 ( Q 2 z,z ) ^ min (41)

при ограничениях

^ ( z ) = 2( Gz,z ) = 1 .           (42)

где функции w, u удовлетворяют условиям периодичности.

3.2. Численный метод

Как и выше, перемещения w ( e ) и u ( e ) будем аппроксимировать сплайнами

n+2

w = £ wj Bj(e), u = £ uj Bj(e), j=0

В самом деле, применяя правило множителей Лагранжа к задаче (41) - (42) , получим уравнение (40) .

Предположим, что оболочка может отходить от наполнителя при w >  0 , т.е. сила реакции наполнителя имеет вид

Cw - = C min { 0 , w} = — *2-( |w| — w ) ,    (43)

где B j ( e ) определяются формулами (6) с заменой x на e при a = 2 п . Граничные условия периодичности будут выполнены, если положить

а энергия, связанная с упругим наполнителем, вычисляется по формуле

w 0 = w n +2 , w 1 = "w n +1 , w 2 = w n

Ф 1

2 π

= п

C ( w - ) ² a ( R + a cos e ) de.

Пусть v ( 9 ) 2 п -периодическая функция, и определим функционал

Ф 2 = 2 п

2 π

C

—v ² ( 9 ) a ( R + a cos 9 ) d9.

Рассмотрим экстремальную задачу

J = J 1 + Ф 2 - PJ 3 ^ min        (45)

w,u,v при ограничениях

{ v ( 9 ) — w ( 9 ) <  0 ,

I v ( 9 ) <  0 .

Ясно, что задача (45) - (46) эквивалентна задаче минимизации функционала

Ф = J 1 + Ф 1 — PJ 3 .          (47)

Далее для исследования задачи (45) можно применить метод, описанный в параграфе 2.2.

При конечномерной аппроксимации функционала Ф 1 вместо функции f ₂ ( z ) получаем функцию f ₂ ( z ) . Поэтому уравнение (40) не имеет места, ибо матрица Q2 не существует. Заметим, что f ₂ ( z ) является положительно однородной функцией, т.е. для любого а >  0 следует f ₂ ( az ) = а ² f ₂ ( z ) , поэтому в данном случае вместо задачи (41) - (42) получаем задачу минимизации функции

ф( z )=^( Q 1 z,z ) + f 2 ( z ) ^ min (48)

при ограничениях (42) . Функция Ф( z ) является непрерывно дифференцируемой, но не имеет непрерывных вторых частных производных.

Для решения задач (41) - (42) применялся метод последовательных приближений [5]: пусть z 0 – начальное приближение, причем £ ( z 0 ) = 1 . Пусть получена точка z k . Тогда z k +1 есть решение задачи выпуклого программирования

Ф(z) ^ min при ограничениях

( Gz k ,z ) = ( Gz k ,z k ) = 2 .

Пусть ak = ^ (zk+1). Тогда zk+1      , zk+1.

α k

Можно показать, что любая предельная точка последовательности zk является стационарной, т.е. удовлетворяет правилу множителей Лагранжа д Ф ∂z

= ^Gz *

где µ – обобщенное собственное число и z _∗ – собственный вектор.

3.3.    Результаты численных экспериментов

В работе [3] на основании линейной теории тонких оболочек приведена формула критического нормального давления для торообразной оболочки:

ψEh

a (1 — v ² ) ’

где

4 k ² ( n ² + ¹ - 2 V n ² k ² + (1 + v ) ² k ² + (1 + v ))

^ =                               +

(4 + k ² ) ( n ⁴ (2 + k ² ) + (1 + v ) k ² n ² )

• 2 h ²      ( ^{n 2 — 1 +} ^ ² 2 k ² ) ( ^{n 2} (1 ⁺ k ² ) ^{+ k} 2 )

⁺ 3 a ² (4 + k ² )        n ² (2 + k ² ) + (1 + v ) k ^{2        +}

h2k2

+ 6a2 (4 + k2) ’ k = RR, n = 1,2, 3... и n выбирается из условия минимума q в (50).

В табл.2 приведены значения критического параметра

h3

q 12(1 — v2) P и значения параметра q, вычисленные по формуле (49). Из табл.2 видно, что при используемой в работе аппроксимации наблюдается удовлетворительное совпадение с теоретическими результатами.

Таблица 2

Сравнение результатов с известными значениями критического давления

h	0.346	0.346	0.346	0.489	0.489	0.489
R	20	15	15	10	15	20
a	5	5	4	2.5	5	5
q	0.012	0.017	0.021	0.036	0.014	0.022
q	0.012	0.012	0.019	0.037	0.017	0.017

В табл.3 введены следующие обозначения: C – жесткость наполнителя, q ^∗ – значение критического параметра в случае жесткой связи с оболочкой упругого наполнителя (см. (34) ), q * - значение критического параметра в случае, когда оболочка может отходитьот наполнителя (см. (44) ), q -значение критического параметра для оболочки без наполнителя ( C = 0) .

Таблица 3 Значения критического давления для торообразной оболочки с упругим наполнителем внутри

h	0.346	0.346	0.346	0.346	0.489	0.489
R	20	20	15	15	20	20
a	5	5	5	5	5	5
C	1	3	1	3	1	3
q ∗	0.017	0.026	0.022	0.030	0.034	0.058
q ∗	0.015	0.021	0.021	0.026	0.029	0.041
q	0.013	0.013	0.017	0.017	0.017	0.017

Таким образом, учет условия “односторон-ности“ контакта оболочки и наполнителя является необходимым при решении задачи на устойчивость. Отметим, что в работе использовалась точная нелинейная теория оболочек. На необходимость применения нелинейной теории оболочек при решении задач на устойчивость указывается в работе [4].