Объединенный метод конечных элементов и граничных элементов для анализа дифракции света на дифракционных решетках

Теория рассеяния на периодических структурах, обычно называемых дифракционными решетками, имеет много применений в микрооптике, например, электромагнитные и оптические средства связи, средства визуализации, определение свойств объектов и поверхностей, электронные и оптические компоненты, фотонные кристаллы, дифракционные решетки [1]. Для моделирования дифракции света на дифракционных решетках были разработаны численные методы, среди которых известны дифференциальные и интегральные методы, методы, основанные на распространении Рэлеевских и собственных мод, вариационные и конечно-разностные методы: метод связанных волн (rigorous coupled wave analysis, RCWA) [2], С-метод [3], методы конечных элементов [4, 5, 6], интегральные методы [7], разностные (finite difference-time domain, FDTD) методы [8, 9].

Вариационные методы наиболее эффективны для неоднородных задач со сложными геометриями. Этот метод требует решения линейной системы уравнений с разряженными матрицами. Для уменьшения размера вычислительной области расчет поля вдали от области вычисления может быть осуществлен с применением интегрального соотношения. Материал периодической структуры может быть диэлектрическим, проводящим, сверхпроводящим, размеры неоднородностей могут быть сколь угодно малыми. Углы в профиле геометрии структуры могут быть учтены в расчете соответствующим выбором сети дискретизации.

В качестве частного случая вариационных методов может быть рассмотрен метод конечных элементов (МКЭ), примененный к эллиптическому уравнению Гельмгольца в области расчета. Он включает выбор схемы дискретизации, построение и минимизацию функционального соотношения. Полученное соотношение преобразуется в систему линейных уравнений, являющуюся неполной без применения граничных условий.

К граничной задаче, удовлетворяющей условиям излучения Зоммерфельда, могут быть применены методы интегральных уравнений, соответственно стандартная методика граничных элементов также может быть использована для периодических задач. Оба метода соединяются на границе между внешней и внутренней частями, с удовлетворением условий непрерывности поля. Использование метода конечных элементов для определения поля внутри объекта приводит к матрице трехдиагонального вида, что требует меньше компьютерной памяти и времени вычисления, чем методы объемных интегралов. Результатом использования метода граничных элементов для определения поля на границе является более точное решение, чем применение метода конечных элементов с условиями поглощающей границы из-за сильной зависимости последних от угла падения поля на границу.

В настоящей работе описывается формулировка объединенного метода для задач рассеяния света на периодических объектах на основе метода конечных элементов и метода граничных элементов (ПМКЭ-ГЭ). С помощью разработанного метода ПМКЭ-ГЭ и RCWA метода [10] было проведено сравнительное моделирование дифракции света на одномерной диэлектрической дифракционной решетке. Сравнение результатов моделирования приведено для ТЕ- и ТМ-поляризованных волн.

Дифракция на периодических структурах

Рассмотрим дифракцию плоской волны с волновым вектором k = k ( sin ( 9 ) , - cos ( 9 ) ,0 ) , k = k ₀ 4s на диэлектрической периодической структуре с периодом d , k 0 – волновое число волны в свободном пространстве

,    2n k0 = ""Г" , Ai где λ0 – длина волны в свободном пространстве, s - диэлектрическая проницаемость среды.

Свет, дифрагируя на структуре, создает рассеянное поле. Кроме некоторой затухающей части дифрагированный свет расщепляется на конечное число отраженных и прошедших поляризованных плоских волн, направление распространения которых не зависит от геометрии и материала периодической структуры, а только от периода решетки. Полное поле определяется как сумма рассеянного и падающего полей. Цель задачи – определить амплитуду и фазу отраженных, прошедших и затухающих порядков.

Геометрия задачи приведена на рис. 1, где R n и T n – коэффициенты отражения и пропускания дифракционных порядков. Для приведенной геометрии задачи можно выделить три зоны с различной диэлектрической проницаемостью: область над структурой при у >  a ( Р 1 ), где a - максимальная высота структуры с постоянной диэлектрической проницаемостью е = £ 1 , область структуры 0 <  у <  а с диэлектрической проницаемостью £ = £ ( x, у ) и область у < 0 ( Р 3 ) с постоянной диэлектрической проницаемостью £ = £ 3 .

Задача дифракции плоской волны на одномерной периодической структуре сводится к рассмотрению двух независимых задач: задачи дифракции плоской волны с ТЕ-поляризацией ( E z * 0, H z = 0) и задачи дифракции плоской волны с ТМ-поляризацией ( H z * 0, E z = 0) [11].

Полное поле u _Q ( x , у ) в области Q (0 <  x <  d , 0 <  y <  a ) должно удовлетворять уравнению [12]:

V-

1 p ( x , y )

^V u q ^{( x} , У )

⁺ к o² q ⁽ x , у ) u q ⁽ x , у ) = f , , ⁽¹⁾

где fq = jkоZо Jz, P(x, у) =Mr, q(x, у)=£ для TE - поля ризации и fQ = -

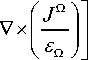
- z, P (x, у)=£, q (x, у) =Mr для TM - поляризации. Константы Mr и £r представляют собой отношение магнитной и диэлектрической проницаемостей среды к аналогичным показателям свободного пространства, т.е. мг=Мм0 и £r= £/£0, Z0 = ^м0 / £0 - импеданс свободного пространства, (Jx, Jy, Jz) – вектор плотности электрического тока источника в области Q. Для TE-поляризации комплексная амплитуда u(x, y) обозначает полное электрическое поле Ez(x, y), направленное вдоль оси z (вдоль образующей цилиндрического оптического элемента), координаты (x, y) лежат в плоскости нормального сечения. Для TМ-поляризации комплексная амплитуда u(x, y) обозначает полное магнитное поле Hz(x, y).

Для решения уравнения (1) область расчета Q должна быть ограничена введением искусственной границы Г = Г 1 + Г 2 + Г 3 + Г 4 (см. рис. 1). Г 1 и Г 3 – фиктивные границы, бесконечно простирающиеся параллельно оси х по координатам y = a и y = 0. Соответственно, для единственного решения задачи на данной искусственной границе должны быть введены граничные условия.

Так как пространство в зонах Р 1 и Р 3 однородное, то поле в них может быть определено в терминах граничных интегралов с соответствующей функцией Грина. Полное поле u Ψ ( x , y ) в этих зонах должно удовлетворять уравнению:

V-

- V и р ( £ ) ^p

+ к о² qu р ( £ ) = f _Р , ^ е Т,

где fр = jkоZо Jz , P = Мт, q = £т для TE-поляризации и fр = -

Vx

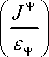
- z , P = £ т ,

q = м _Т для TM - поляризации. J ^Т - вектор плотности электрического тока источника в области Р , область Р = Р_ь Р 3 .

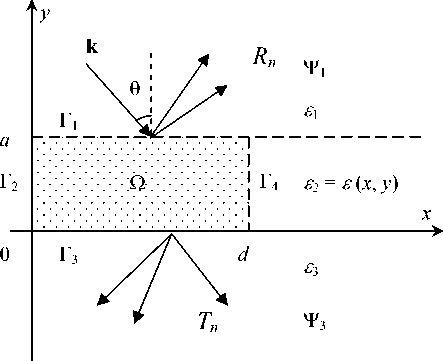
Рис. 1. Геометрия задачи дифракции на периодической диэлектрической структуре

Описание метода расчета

Метод решения уравнения Галеркина (1) основан на решении соотношений вида:

Я Г 1                 ,),,-.„

I-- А и _fi у - qk и _fi y - f , Y |- d ^ = 0, q I P                   )

где γ - произвольная функция из области определения уравнения (1).

Используя первую формулу Грина:

Л PАQdQ = j P—Qdl - Л VPVQdQ, Q          г dn    Q для функций P и Q, где Q - область плоскости x, у;

Г – ее граница, обходимая против часовой стрелки;

dQ d n

– производная в направлении внешней нормали к кривой Г, получим:

Я Г 1

— Vип (x, у)Vy - qk ип (x, у)Y dQ-Qx•

Q \ p7

- J

L duoix,^Г .Jf/a,dQ. p   dn

г

Систему базисных функций для Q обозначим {®Qk,l(x, у)} Nx =Nу и систему базисных функций для Г обозначим {^Г„(x, у)} М=1, где Nx, Ny - число узлов сеточного покрытия прямоугольной области Q по оси x и y соответственно, М – число узлов сеточного покрытия границы Г.

Подставляя в соотношение (4) вместо произвольной функции γ систему базисных функций для метода Галеркина, можно записать систему линейных уравнений:

где Г m , s – линейная область границы Г , включающая узлы границы m и s .

Элементы матрицы C вычисляются по формулам:

C Ny ( k ) + 1 , Ny ( i) _{+ J} = JJ ® Q 1 ( x , У ) ^ " ( x , y ) d Q ,        (13)

Q k , 1

A u + B v = C f ,

где u = ( u 1 , ..., u _NxNy ) ^T – вектор, составленный из ко-

эффициентов

N x , N y

{ u Ny ( k ) + l } k , 1 = 0

разложения:

Nx,Ny u Q (x, У) = E uk, 1юк,1 (x, У).                (6)

k , 1 = 0

Вектор f = ( f 1 , ..., f _NxNy ) ^T – вектор, составленный из коэффициентов разложения:

Nx,Ny fQ (x, y) = E f,1®i(x, y).                    (7)

k , 1 = 0

Хотя равенства (6) и (7) действительны для всех точек ( x , y ) в области Q , необходима отдельная обработка величин поля и его частных производных на границе Г от значений во внутренней области. Разложение, аналогичное (6) и (7), для поля и его частных производных на границе имеет вид:

M u Г( x, У) = Eum^m (x, у ),(8)

m = 1

M v Г(x, У ) = E vm®m (x, У)’ m=1

M fГ(x, У) = E fm»®m (x, Уh m=1

k , i = [1, N x ]; l , j = [1, N y ], где Ω k , j – область разбиения области Ω, включающая узлы сети k и j .

В качестве кусочно-линейного базиса была определена функция вида:

1 x — x 1- kh _ У1- У h, если x, y e Qk1J ®L1(x, У) = ■ 1-xk—x h 1+y-zy h если x, y e 0^12 если X, y e ^1,3 ,(14) 1+xk—x h +У1_ У h, если x, y e Qk14 1+xk—x h , если x, y e Qh,1i5 i У1- У I1- h , если x, y e ЙЦ6 где h – длина сегмента сети покрытия.

Элементы ( а ⁱ _k ^, _, ^j _l ) матрицы А , элементы ( b m , s ) мат-

рицы В и элементы ( с ⁱ _k ^, _, ^j _l ) матрицы С вычисляются из уравнений (11), (12) и (13) соответственно. Тогда систему уравнений (5) можно представить в виде:

где ( x , y ) e Г, v = ( v 1 , ..., v_M ) ^T - вектор, составленный из коэффициентов разложения v k .

Элементы матрицы А вычисляются по формулам:

[ A Q , Q ] [ A F , a ] [ ^A Q , r ] [ A F . r ]

[ B ]

u Q

u

Г

v

Г

aN y ( k ) + 1 , N y ( i ) + j =

= JJ Q k,1	1	e ®k2 1 ( x , y ) em j1j ( x , y ) + d x       d x
	p ( x , y ) I	+ дю к 2 1 ( x , y ) 5 ® ," j ( x , y ) _+     d y         d y    _

— k 02 q ( x , У )«k , 1 ( x , У ) ®kj ( x , У ) ) d Q ,

k, i = [1, Nx]; l, j = [1, Ny], где Ωk, j – область разбиения области Ω, включающая узлы сети k и j.

Элементы матрицы В вычисляются по формулам:

bm, S =- f ®>Sd1 , г m,s m, s = [1, M],

= ^ C ^Q , ^{Q ]} ^ C ^{rj2 ]} lr f Q "

[[ C Q ,Г ][ C Г,Г ]][ f r J

Система уравнений (15) не имеет единственного решения, так как она состоит из N равенств с N+M неизвестными: N = N_xN_y – общее число узловых величин поля u_k , ₁ ( x , y ) в области Q u M производных по нормали на граничных узлах v_{k , l} ( x , y ).

Определим граничные условия для поля и его производных на границах Г 1 и Г 3 , удовлетворяющие уравнению (2).

Для построения граничного интегрального уравнения на основе уравнения (2) для поля и его нормальной производной введем функцию Грина u ^*, удовлетворяющую условиям излучения Зоммер-фельда и являющуюся фундаментальным решением уравнения Гельмгольца:

V ² u * ( ^ , n ) + k ² u * ( ^ , П ) = -5 ( ^ , П ), n e ^.       (16)

Фундаментальное решение для уравнения Гельмгольца в двумерном однородном пространстве известно и равно

u • ( f , n ) = ( i /4) H 01 (kr ),                          (17)

где r = V [ ^x( n ) - ^{x ( f} ) ] 2 + [ y⁽ n ) - у ( ^ ) ]² ,

H ₀ ⁽¹⁾ ( kr ) = J 0 ( kr ) + iY 0 ( kr ) – функция Ханкеля первого рода и нулевого порядка, где J 0 – функция Бесселя первого рода нулевого порядка, Y 0 – функция Неймана нулевого порядка.

Для построения граничного интегрального уравнения для рассеянного поля и его нормальной производной в зонах V ₁ и V 3 воспользуемся теоремой Грина в следующем виде:

J [V ² u * ( f , n ) + k ² u * ( f , n ) ] u ( n ) d T =

V

где φ - внутренней угол кусочно-линейной границы в точке £. Первое слагаемое в правой части (19) является полем, создаваемым источником fΨ в свободном пространстве, и может быть обозначено как па-in дающее поле uу .

Таким образом, уравнение (19) записывается в следующем виде:

c ( f ) u ( f ) = J V ( n ) u * ( f , n ) d Г-

Г'

J u ( n ) ^d u ^fn ) d Г + u V ( f ).

Г       d n

Поле u и его производные v в случае дифракционной решетки являются квазипериодическими функциями [11, 13-15]:

= - J v ( n ) u * ( f , n ) d Г +

Г'

u ( X , У ) = й( X , У ) e^k ° ^a ° x , V ( X , у ) = v(X , у ) e i ^{0 а 0}x ,

+ J u( n ) ^d u ^{( f n} ) d Г + J f _P ( n ) u* ( f , n ) d V , Г'          o n            '

du (n) где v(n)    , , dn

- нормальные производные поля,

под Г' принимаются бесконечные границы у = а и

у = 0 для зон V и 4' 3 соответственно.

Подставляя равенство (16) в уравнение (18) и осуществляя предельный переход точки наблюдения ξ из внутренней в граничную, найдем

где й(x , у ) и v(x , у ) - периодические по x функции с периодом d .

Интегрирование по бесконечной границе Г' в (21) можно заменить интегрированием по границам Г 1 и Г 3 :

2 u ⁽ x 0 , у ) =

го

= J Е v(.x , у ) ё^к0 “ ^{0(x + nd} ) u * ( x + nd - x ₀) dx - Г n =-го

c ( f ) u ( f ) = - J f V ( n ) u * ( f , n ) d V +

V

+ J V ( n ) u * ( f , n ) d Г - J u ( n ) ^d u ^{( f} ,’ ⁿ ) d Г .

T'                      T'          dn

го

^- J Е ^^^{( x ,} у ) ^e

Г n =-го

, ik 0 „ 0 ( x + nd ) ^{d u} * ^{( x + nd - x} 0 ) _dx +

+ u^m ( x 0 , у ), x е [0, d ),

d n '

Это уравнение обеспечивает связь между полем u и его нормальной производной V на границе Г' . Функция c ( f ) в уравнении (19) равна:

c ( f ) = 1 —     ^ ,                                  (20)

2 п

где Г = Г 1 , Г 3 , y = a и y = 0 для границ Г 1 и Г 3 соответственно.

Подставляя вместо функции комплексной амплитуды в уравнении (23) на границе ее аппроксимацию базисными кусочно-линейными функциями (8) и (9), получим соотношение (24).

1                        M      I                   го                              1

- ^u _r i ^{( x} s ) = Е h 1 v Г , ^{( x} m ) Е e ik ⁰ “ ^{0 ( x} m ⁺ nd )   J ® ^Г ' ( ^x m ⁺ h n ) u Г , ( ^x m ⁺ n^d - ^x s ^{+ h} n ) ^d n

²                m = 1    I            n =-го                  - 1

го

- u r , ( x m ) Е e ik ° “ ^{o ( x} m ⁺ nd ) n =-ro

J ® ^Г ( ^x m ⁺ h n )

- 1

d u Г , ( x m + nd

-

d n '

x s + h n )

d n

+ u Г ( x s ),

где s = [1, N x -1], i = 1, 3.

Граничные условия на поле и его производные на границах Г 2 и Г 4 являются периодическими вида:

u_T = u_re ^k - " - d , V = v e ik ° " ⁰ d .                    (25)

1 4          1 2             ’ ¹ 4           ¹ 2                                                          ^{V 7}

Разложения (8) и (9) и граничные условия (25) позволяют записать для коэффициентов поля и его производных на границах Г 2 и Г 4 :

^u Г ₄ ^{( x} s ) = ^u Г ₂ ^{( x} s ) e^k 0 ^a 0 d , v Г ₄ ^{( x} s ) = v Г ₂ ^{( x} s ) e ik ° ^a ° d , ⁽²⁶⁾

где s = [1, N y ]. Элементы матриц D и G , соответствующие границам Г 2 и Г 4 , записываются как:

d2s = 1, d4s = dsei0a0d , g2s = 1, g4 = gseik0a0d , e2s = 0, e4 = 0, s = [1, Ny].                         (27)

Соотношения (24) могут быть представлены в матричном виде (30) с элементами матриц D , G и E вида (27), (28) и (29). Бесконечные ряды в (28) и (29) аппроксимируются конечными суммами с относительной погрешностью менее 10^-5.

X

di• m = - h J у

e i 0 ^a 0 ( x m ^{+ nd} )

n =-X

f r z , /u Г ( x m ⁺ n^{d -} I to ‘ ( x m + h r )---------—-

- 1                           d n

x s ⁺ h r ). _s ---------ddr] ^ , e i

=18 ,

₂ s , m

gS , m = h J j^ e ik 0 « 0 < + nd ) I n = -X

J tori (xm + hr) иГ. (xm + nd - xs + hr) dr

- i

m , s = [1, N x -1], i = 1, 3.

[ D ] u r + [ G ] v r = [ E ] u n .

Интегралы в равенствах (28) и (29) могут быть оценены численно. Объединяя системы уравнений (15) и (30), получим замкнутую систему линейных алгебраических уравнений для решения задачи дифракции плоской волны на периодическом двумерном микрообъекте (31).

Поле в областях V 1 и V 3 может быть представлено в виде разложений Рэлея (суперпозиций плоских волн). В зоне Т 1 z -компоненты полей имеют вид:

и ( x , y ) = exp ( ik о ( a, x - в о У ) ) +

X

⁺ У R n exp ( k 0 0 ( ^a n x ⁺ Р и У ) ) , n =-X

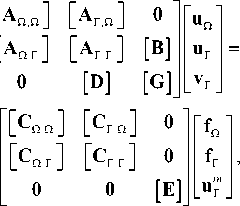
где a n

V S " sin ( 9 ) + n ^d- , P n = V S j - a n .

Функция u ( x, y ) представляет компоненту Е z ( x, y ) электрического поля для случая ТЕ-поляризации и компоненту H z ( x, y ) магнитного поля для случая ТМ-поляризации.

В зоне ^ 3 z -компоненты имеют вид:

где подматрица А Ω,Ω размерностью ( N – M) ×( N – M) включает в себя коэффициенты соотношений поля во внутренних узлах сети разбиения, подматрицы А _Ω,Г и А _Г,Ω размерностью ( N – M) × M и M ×( N – M) соответственно включают в себя коэффициенты связи поля в граничных и внутренних узлах, подматрица А Г, Г размером M × M включает в себя коэффициенты связи поля в граничных узлах, подматрица В размером M × M включает в себя коэффициенты соотношений между производными поля на границе и полем во внутренних узлах сети разбиения, подматрица D размером M × M включает в себя коэффициенты связи поля свободного пространства в граничных узлах, подматрица G размером M × M включает в себя коэффициенты соотношений между производными поля на границе и полем свободного пространства во внутренних узлах сети разбиения. Подматрица С Ω,Ω размерностью ( N – M) ×( N – M) включает в себя коэффициенты соотношений источников поля во внутренних узлах сети разбиения, подматрицы С Ω,Г и С Г,Ω размерностью ( N – M) × M и M ×( N – M) соответственно включают в себя коэффициенты соотношений источников поля в граничных и внутренних узлах, подматрица С Г, Г размером M × M включает в себя коэффициенты соотношений источников поля в граничных узлах. Подматрица E имеет размер M × M. Вектора u_Ω и u_Г – вектора напряженности поля во внутренних и граничных узлах сети, v _Г – вектора нормальных производных поля в граничных узлах сети. Вектора f Ω и f Г – вектора источников поля во внутренних и граничных узлах сети, и _Г - вектор напряженности внешнего падающего поля в граничных узлах сети. Таким образом, система (31) имеет N + M уравнений и столько же неизвестных.

X

и ( x, У )=S Tn exP (k0 (anx - РпУ )) ,          (34)

n =-X

где ^P n = Д^S 3 - ^a 2 .

Разложения Рэлея (32), (34) являются решениями уравнения Гельмгольца

A и + k2 и = 0 ,

при k ² = k 02 S 1 и k ² = k ₀ ² s ₃ , соответственно.

После определения значений поля в области Q и его производных на границах Г 1 и Г 3 нормированные интенсивности отраженных и прошедших порядков рассчитываются следующим образом [1, 5, 6]:

тR — I р I^{2 P}n т^т — i ^ l I^{2 P}n

I- =^{| Rnl} Ik¹1" = S^TT'¹ Pk’

S i-t = J n £U 3         J

тr_|p |2 p- jt _ ^i It I2 pn In"'Rnl Pk’ I- =SPTTnl Pk’

f У iR + У ITT = 1

I n                  n

I n e U J          n e U 3

для ТЕ- и ТМ-поляризованных волн соответственно. Выражения (37), (38) определяют, какая часть энергии падающей волны перейдет к n -му порядку дифракции. Заметим, что интенсивности порядков распространения существуют для непоглощающих материалов, т.е. для Im Js = = 0. Множества U 1 и U₂ в (37) и (38) являются множествами индексов, соответствующих отраженным и прошедшим порядкам дифракции:

U 1

= 1

n e Z: -^ <  1

^ 1

если

Im 4ё\ = 0

, U 3 = 1

n e Z:

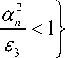
если Im J&= = 0

0,

если Im ^s_x >  0

0,

Для определения коэффициентов отражения R n и пропускания T n воспользуемся дискретным преобразованием Фурье:

1 N - 1

R n ,E [ u ( X k , a ) - u iⁿ ( X k , a ) ] exP( - ^ik° ^a n^Xk ) (40)

N k = 0

1 N - 1

T n = E u ⁽ x k ^,0)eX P ^{( -} ik ^,/X. ). (41)

N k = 0

Эти коэффициенты описывают амплитуду и фазовый сдвиг распространяющихся плоских волн. Более точно, модули R_n и T_n – это амплитуды n -го отраженного и прошедшего порядков и arg [ R n/ R n |] и arg [ Tnl\Tn I] — фазовый сдвиг. Коэффициенты с n t U ₁ n t U ₃ описывают затухающие волны.

Результаты численного моделирования

Рассмотрим в качестве примера дифракцию плоской волны с длиной волны Л ₀ = 0,6 мкм на бинарной диэлектрической дифракционной решетке с коэффициентом заполнения 0,25 с толщиной 0,24 мкм. Период решеток менялся от 0,2 мкм до 2 мкм. Соответственно при моделировании ПМКЭ-ГЭ длина сегмента сети покрытия h менялась от Л ₀ / 300 до 2 ₀ / 30 .

Рассмотрим пример. Плоская волна падает по нормали из воздуха ( г ₁ = 1) на решетку ( е ₃ = 2,25). На рис. 1 и 2 представлены зависимости эффективностей I ₀ ^R и I ₀ ^T порядков дифракции ТЕ- и ТМ-поляризованной волны соответственно от периода решетки.

Зависимости отклонений интенсивностей A I R и A I T ( A I = | i i^RCWA - у ™®^- ГЭ |) нулевых порядков дифракции, рассчитанных RCWA и ПМКЭ-ГЭ методами, ТЕ- и ТМ-поляризованных волн от длины сегмента сети покрытия h метода ПМКЭ-ГЭ приведены на рис. 3. Трудно отметить явную зависимость отклонения для h <  Л ₀ / 30 . Равномерная норма отклонения интенсивностей составляет 4∙10^-3 и 2∙10^-3 для ТЕ- и ТМ-поляризаций соответственно.

В следующем примере плоская волна падает по нормали из подложки решетки ( г ₁ = 2,25) в воздух ( е ₃ = 1). На рис. 4 и 5 представлены зависимости интенсивностей I ₀ ^R и I ₀ ^T порядков дифракции ТЕ- и ТМ-поляризованной волны от периода решетки.

Зависимости отклонений интенсивностей A I R и A I T порядков дифракции ТЕ- и ТМ-поляризованных волн от длины сегмента сети покрытия h приведены на рис. 6. Равномерная норма отклонения интенсивностей составляет 7∙10^-3 и 8∙10^-3 для ТЕ- и ТМ-поляризаций соответственно.

если Im Js^> >  0

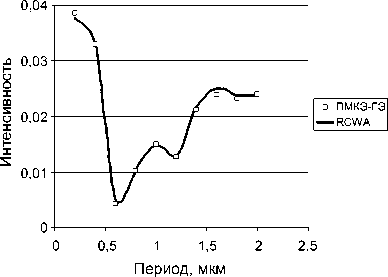
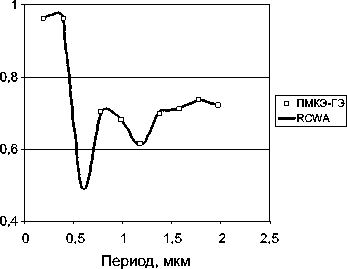
Рис. 2. Распределение эффективности нулевых порядков дифракции ТЕ-поляризованной волны: а) I ₀ ^R , б) I ₀ ^T

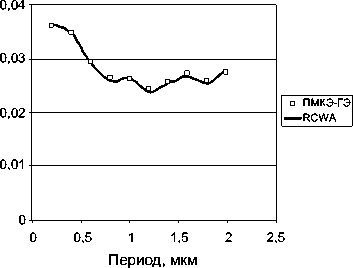
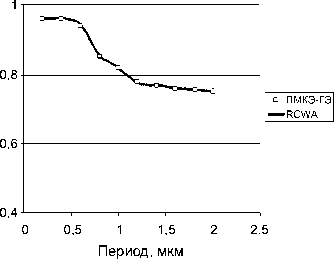
Рис.3. Распределение эффективности нулевых порядков дифракции ТМ-поляризованной волны: а) I ₀ ^R , б) I ₀ ^T

а)

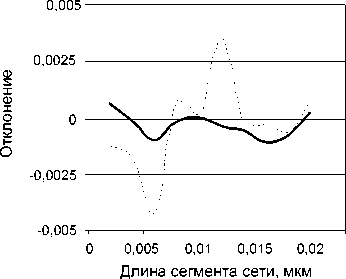
∆ R0

∆ T0

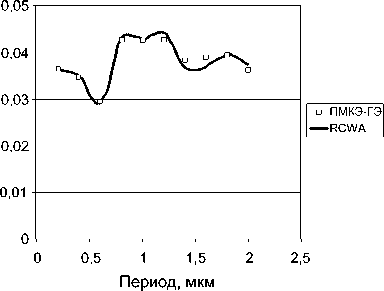
б)

б)

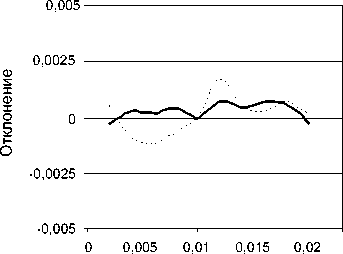
Длина сегмента сети, мкм

∆ R0

∆ T0

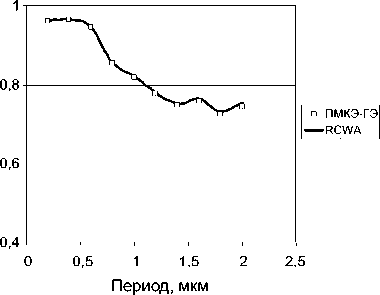
Рис. 4. Зависимость отклонений эффективности нулевых порядков от параметра h: а) ТЕ-волны; б) ТМ-волны

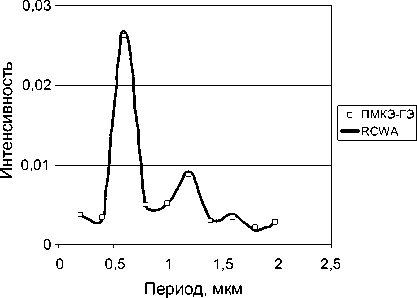
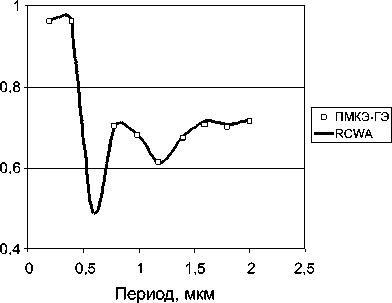
Рис. 5. Распределение эффективности нулевых порядков дифракции ТЕ-поляризованной волны:

а) I ₀ ^R , б) I ₀ ^T

Рис. 6. Распределение эффективности нулевых порядков дифракции ТМ-поляризованной волны:

а) I ₀ ^R , б) I ₀ ^T

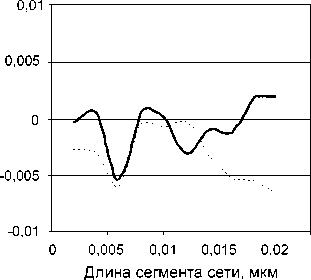
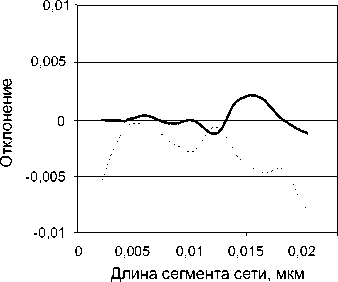
Рис. 7. Зависимость отклонений эффективности нулевых порядков от параметра h: а) ТЕ-волны; б) ТМ-волны

Таким образом, сравнение результатов, полученных разработанным ПМКЭ-ГЭ методом и RCWA методом, показало их хорошее соответствие.

Заключение

В данной работе представлен объединенный метод конечных элементов Галеркина и граничных элементов для решения задач дифракции плоской электромагнитной волны на периодических неоднородных двумерных (цилиндрических) объектах микрооптики, период которых сравним с длиной волны.

Проведено исследование зависимости относительной погрешности результатов моделирования от отношения длины волны падающего света к длине сегмента сети покрытия.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-SA-06), гранта РФФИ 08-07-99007-р_офи, Фонда содействия отечественной науке и гранта Президента РФ поддержки ведущих научных школ (НШ-3086.2008.9).