Объемное формирование цилиндрического изделия с учетом давления

Широкое использование полимерных материалов с различными вязкоупругими свойствами обосновывает развитие математического моделирования процессов получения изделий из данных материалов. Методы исследования напряженно-деформированного состояния полимерных изделий различной геометрии разрабатываются при решении задач в области электроники [1], строительства [2], медицины [3] и т.д.

В работах [4–10] рассмотрены математические модели формирования полимерных осесимметричных изделий при реализации различных режимов проведения реакции полимеризации (отверждения) — объемный, односторонний фронтальный, фронтальный с двусторонним фронтом [11]. Для объемного режима характерно протекание отверждения — повышение температуры и углубление степени полимеризации — во всем объеме формируемого изделия. Фронтальный режим отличается распространением волны (фронта) отверждения от одной граничной поверхности изделия к другой (односторонний фронтальный режим) либо из центральной области изделия к граничным поверхностям (двусторонний фронт). Разработанные модели объединены в единый программный комплекс [12].

Определение уровня внутренних напряжений основано на использовании закона наследственной упругости — интегральных уравнений типа Вольтер-ра, записанных в тензорном виде [13]. При рассмотрении объемного режима отверждения [4] критическая глубина конверсии материала предполагалась равной нулю. Под критической глубиной конверсии следует понимать степень полимеризации (концентрация заполимеризованного мономера а = а ( r, t ) , при которой в твердеющем материале определяются вязкоупругие напряжения и деформации. При анализе фронтального режима — как одностороннего [7–9], так и двустороннего [11] — учитывались условия сосуществования твердой и жидкой областей формируемого изделия. При этом на границе сосуществования задавался полный тензор напряжений. Условием возникновения твердой части и ее роста является достижение глубиной полимеризации а ( r, t ) критического значения. Естественно считать, что аналогичный подход может быть реализован и в объемном режиме реакции. Теоретические вопросы рассмотрения такого подхода изложены в работе [14].

Распределение температуры T = T(r, t), глубины полимеризации а = а(r, t) и глубины кристаллизации п = П(r, t) определяется на основе макрокинетической модели совмещенного процесса [15]: уравнения теплопроводности и двух кинетических уравнений относительно степеней полимеризации и кристаллизации. В зависимости от условий проведения реакции отверждения реализуется объемный или фронтальный режим реакции. В настоящей работе не обсуждается метод определения температурных и конверсионных полей в процессе от- верждения: вопросы, касающиеся этой части работы, подробно обсуждены в цитируемой литературе.

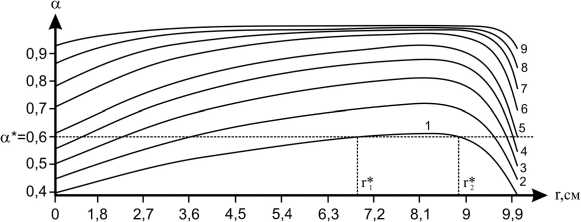
Рис. 1. Динамика степени полимеризации а = а ( r, t ); t(c): 292(1), 300(2), 308(3), 315(4), 322(5), 330(6), 338(7), 345(8), 352(9); r i = r i ( t ) , r 1 = r 1 ( t ) — границы твердого слоя Q в момент времени t = 292 c.

Рассмотрим объемные режимы формирования с ненулевой критической глубиной конверсии. Процесс объемного формирования изделия характеризуется постепенным углублением полимеризации (формирование твердого слоя Q ) и следующей за ней кристаллизации по всему рассматриваемому объему.

Границы r * = r * ( t ) и r * = r * ( t ) твердого слоя и момент присоединения t * ( r ) произвольной точки r формируемого изделия к слою Q определяются условием а ( r, t ) = а * , где а * — критическая глубина конверсии, ( а * = 0 . 5 ^ 0 . 7) (рис. 1).

Формирование цилиндрического изделия

Напряженно-деформированное состояние твердеющего материала (область Q ) можно полностью описать следующей системой определяющих соотношений:

∂σ rr ∂r

ε φφ ∂r

^ фф   ^ rr

r

E rr    ^ фф

r

(1)— уравнение равновесия, (2)— условие совместности деформаций; σ rr , σ φφ — радиальная и окружная компоненты тензора напряжения; ε rr , ε φφ — соответствующие компоненты тензора деформации. Полные компоненты деформации в (2) являются суммой вязкоупругой е * , температурной e^t = а 0 ( T — T 0 ) и химической E ch = E p + E _cr составляющих ( E p = k 1 а, E _cr = k ₂ п — усадки вследствие полимеризации и кристаллизации, соответственно):

E = E * + E T + E ch .              (3)

Здесь α 0 — аналог коэффициента линейного температурного расширения материала; для простоты будем считать его постоянным; k 1 , k 2 — константы.

Будем считать слой Q твердым, а остальную часть объема — жидкой. Тогда в двумерном случае вязкоупругая компонента деформации ε ^∗ связана с напряжениями выражением:

( ^E r_r ^{( r,t} )) =

^Е фф ^{( r,t} )

1 /E  -v/E\(a _TT ( r,t )\

= -vv)E  1 /E )^фф ( r,t )J ⁺      (4)

В изображениях, т.е. для вязкоупругого цилиндра, зависимости (8) примут вид

t

₊ f ffrr ( t - T )

⁺ J \fP ⁽ t ^{- T} )

t * ( r )

f ry ⁽ t ^{- T} P ( ^O rr ^{( Г,т} A d_T ф ⁽ t - ^T p ^ фф ^{( Г,т} p ’

err (P) = ефф(P) =

где ε _r ^∗ _r , ε ^∗ _φφ — радиальная и окружная вязкоупругие компоненты деформаций; σ rr , σ φφ — соответствующие компоненты напряжений; ν — коэффициент Пуассона; E — модуль упругости среды Гука; t * ( г ) — момент присоединения точки г к твердому слою Q .

Запишем (4) покомпонентно:

E ( p ) P rr ⁽ p ) ^{- v (} p ) σ _φφ ( P ) , E 1 p ) ( ^О фф ⁽ P ) ^{- V (} P ) ^O rr ⁽ P )) .

Сравнивая (7) и (9), получим формулы для неизвестных операторов K ij ( p ) :

K rr ( P ) =

∗ rr

= E ^{( O} rr ^{( r,t} )

К фГ ( P ) =

E ( p ) ’ ^{v (} p )

-

-

VO фф ( Г, t )) +

+

t frr (t   T) Orr(Г’ T ) dT +

Следовательно,

F rr ( P ) = F фф ( P )

К гф ( P ) = -

E ( P )

^К фф ^{( p} ) =

eM

E ( P ) ’

E W .

t * ( r )

t

+      ^/гф ⁽ t ^T ) ^O фф ( Г, T ) dT,

F rф ( P ) = F фr ( P )

^{E (} p ) ^{v (} p )

-

P f

_E , f _rr

^∗ ε φφ

t * ( r )

= e ⁽ Ст фф ^{( r,}t )

-

VO rr ( r,t )) +

+

t j /ФГ (t T) Orr(Г’ t ) dT +

t * ( r )

t

+      ^/ фф ⁽ t   ^T ) ^O фф ( г, т ) dT.

t * ( r )

Применим к (5)–(6) преобразование Лапласа e rr ( P ) = O rr ( P ) ( e + F rr ( P )) +

^{+ O} фф ^{( p} ) ^ ^F rф ^{( p} ) ^— e^ =

= Krr (P) Orr (P) + Кгф (P) Офф (P), ефф(p) = стфф (p) ^e + Fфф(p )^ +

+ O rr ( P ) ^ F ^r ( P ) — E^ =

= ^К фф ^{( p} ) σ φφ ( p) + К фг ( P ) σ rr ( P ) .

В соотношении (7) e rr ( P ) , е гф ( p ) , e ^r ( p ) , е фф ( p ) , O rr ( p ) , О гф ( p ) , О фг ( p ) , О фф ( p ) — изображения соответствующих деформаций и напряжений; F rr ( P ) , F _rф ( P ) , F _фr ( P ) , F _фф ( P ) — изображения неизвестных функций f rr ( P ) , / гф ( P ) , / фГ ( P ) , / фф ( P ) .

Для упругого (бесконечного) цилиндра, нахо-

дящегося в условиях плоского напряженного состояния, закон Гука запишется как

ε rr

E ^{( O} rr

^{— vO} фф ) ,

^е фф —

E ^{( О} фф

— VO rr ) .

-

E ( P )

ν

⁺ E’ ^/гф =

^/ фф i

f φr ^.

Найдем выражение для неизвестного оператора v ( p ) . Воспользуемся условием несжимаемости материала. Для упругого материала с учетом e zz = 0 выполняется соотношение

err + ефф — 0 ’ а для вязкоупругого —

^e *r ^{( r,t} ) ^{+ е} фф ^{( r,t} ) = ⁰

С учетом (5), (6), (10) последнее соотношение в изображениях запишется:

F rr ( P )( O rr ( P ) + О фф ( P )) +

^{+ F} rф ^{( p )( O} rr ^{( p} ) ^{+ O} фф ^{( p} ))    ⁰ .

Следовательно,

V ( p ) = 1 - P —^V E ( p ) .          (11)

E

Тогда из (10)

^ Гф ⁽ P ) = ^F фr ⁽ P ) = eE ^- E 1 p ) = -F rr ⁽ P ) . ⁽¹²⁾

Следовательно, frr = /фф = -/Гф = -/фГ.        (13)

Для стандартной модели [4] вязкоупругого тела frr (t) = P-Pe-^t.            (14)

E

Здесь

E = E i ; P = ^E ^ ^+E :r = ^E 2 .

ββ

Для определения радиальной O _rr = O _rr ( Г, t ) и окружной o _фф = o _фф ( r,t ) компонент напряжений введем в рассмотрение функцию напряжений Ф = ^{ф ( r,}t ) ^:

O rr ( r,t )= ^Ф ’ O фф ( r,t )= ^дф,     (15)

r               ∂r

для которой уравнение равновесия (1), очевидно, выполняется. Подстановка полных компонент деформации (3) в уравнение совместности (2), с учетом введенной функции (15), приводит к следующему уравнению [14]:

д Г д Ф Ф

∂r ∂r r

следовательно,

p ( r * ,t ) = — F ^{( r} * ,t ) .              (19)

1 -V

Выберем в качестве функции интегрирования функцию, пропорциональную давлению, т.e.

Ф( t ) = — (1 — v ) p ( r * ,t )

t

+ / f(t - т) (        +      ) dT] + t∗

или

Ф( t ) = F ( r * ,t ) .

∂

+

∂r

E

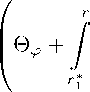
0 r

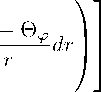
= 0 ,

Тогда, следуя (17), на границе r = r * будет выполняться условие:

„ rr ( r,,) )+ „ фф ( r * ,t ) = 0 ,         (21)

где f ( t ) = Ef rr ( t ); 0( r,t ) = e ^T + e ch ; r * 6 r 6 r * , t * = t * ( r ) — момент присоединения точки r к твердому слою Q . Интегрируя последнее равенство, получим следующее соотношение относительно функции напряжений:

д Ф( r,t ) + Ф( r,t ) + ∂r r

поскольку в этом случае t = t * и интеграл в (17) обращается в нуль.

Рассмотрим границу твердого слоя r = r * . Аналогично предыдущим рассуждениям и формуле (19), получим

p ( r * ,t ) =

F ( r * ,t )

1 — V

t f ~      . /дФ(r, т)   Ф(r, т)\

+ J f ( t — т )( '   + ^T^J dT =  (16)

t ^∗

= -E [_e ф + j^dr ) + Ф( t ) .

^r 1 ^∗

Найдем функцию интегрирования Ф( t ) . Следуя (15), имеем:

^Ф^ + v/ = „„ ( r,t ) +   . ( r,t ) .

r∂r

Из соотношения (16):

Ф( t ) = „ rr ( r,t ) + „ фф ( r,t ) +

t

+ I f (t - T)(„rr (r,T) + „фф (r,T)) dT + t∗

+ F ( r,t ) , где функция

F(r,t) = E |0ф .p /'dr )

r1∗ определяется решением уравнения теплопроводности и кинетических уравнений; 0i(r, t) = ech + eT.

Со стороны жидкого слоя, в силу условия несжимаемости среды, на твердую часть материала действует давление p ( r * ,t ) :

E— ( e^T + e ch ) + p ( r * ,t ) = 0 ,

1 — V

Так как функция Ф( t ) теперь известна (20), из формулы (17) находим, что

„ rr ( r * ,t ) + „ фф ( r ,t) ) = F ( r * , t ) — F ( r 2 * ,t ) (23)

или

„ rr ( r * ,t ) + „ фф ( r,,) ) =

= (1 — V ) ( —p ( r * ,t ) + p ( r * ,t )) .

Введем в рассмотрение функцию J ( r, t ) :

t

J ( r, t ) = Ф( r, t ) + j f ( t — т )Ф( r, т ) dT.    (24)

t ^∗

Тогда уравнение (16) с учетом (20) представимо в виде дифференциального уравнения:

SJ ^ + JM = —F ( r,t ) + F ( r;,) ) .

Cоотношение (25) разрешается аналитически:

∗ r ₂ ^∗

J ( r, t ) = - У F ( r, t ) rdr—

r

— T rF ( rv) ) ( r 2* — r * ) . откуда следует, что

J ( r 2 * ,t ) = 0 .

Для нахождения функции напряжений Ф( r,t ) из уравнения (24) используем преобразование Лапласа. Введем в рассмотрение следующие функции:

ж^     \ 0 ,      t*

^{Ф( r,t} )    | Ф( r,t ) , t >  t * ’

^J( r-t )={ J' ( r,t ) , t< t

относительно которых справедливо уравнение, аналогичное (24):

t

^{ф( r,t} ) ⁺ J f ⁽ t

-

/-V                                                /-V т )Ф( r, т) dт = J (r,t).

Применим к последнему соотношению преобразование Лапласа, тогда относительно изображений Ф( r,p ) , J ( r,p ) с учетом (14) получим выражение:

^^

^ф( r,p ) ^{+ (} А - Ц ^{) Ф(} r’p ) = J ⁽r,p ) Р ⁺ Ц

или

/-w

Ф( r,p )

p ⁺ Ц p + А

J ( r,p ) .

Следовательно, оригиналы связаны уравнением:

Ф( r, t ) = J(r, t ) —

t j (А — ц) exp [—А (t — т)] J (r, т) dT. 0

Обозначим момент времени t появления твердой части Q через t 0 . Для определения напряженного состояния формируемого изделия зададим начальные и граничные условия:

0 6 t < t 0 , Q = 0 : a _rr ( r, t ) = 0 , а _фф ( r, t ) = 0; (30) t >  t о : ( ^ rr ( r,t )+ СТ фф ( r,t )) | r = r * =0 ,

^ rr ( r,t ) | r = r * =0 , (31) ^ rr ( r ⁰ ,t ) + а фф ( r ⁰ ,t ) =

= (1 — v )( —p ( r 0 ,t )+ p ( r 0 ,t )) . (32)

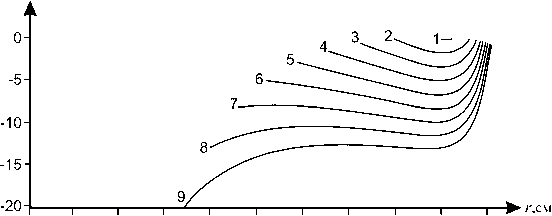
Результаты расчета модели определения напряженно-деформированного состояния изделия в объемном режиме — пространственно-временные изменения радиальной a _rr ( r, t ) и окружной а _фф ( r, t ) компонент напряжения — представлены на рис. 2– 3. Наблюдаем убывающий в каждой точке характер радиальных напряжений, их убывание от внутренней поверхности изделия к внешней. Для окружной компоненты напряжения, напротив, характерно возрастание вблизи внешней поверхности (рис. 3).

Из последнего соотношения получим выражение для функции напряжений Ф( r, t ) :

Ф( r, t ) = J ( r, t ) —

t j (А — ц) exp [—А (t — т)] J (r, т) dт. t∗

Офф^гс/см2

0    1,8   2,7   3,6   4,5   5,4   6,3   7,2    8,1    9    9,9

Рис. 3. Динамика окружной компоненты напряжения: Ст фф = Ст фф ( r, t ); условия на рис. 1.

Отсюда, следуя (15), получим формулы для компонент тензора напряжений — радиальной и окружной:

a _rr ( r,t ) =

rJ ( r,t )

-

t

—у( а t∗

-

ц ) exp [ —А ( t

-

т ^)] J ⁽ г,т ) d^,

Давления p ( r 0 , t ) и p ( r 0 , t ) со стороны жидких слоев на образовавшуюся твердую часть Q будем определять по формулам (19) и (22) (рис. 4).

аФФ (r,t ) = Jr^ — t (А — ц) exp [—А(t — т)] dJ^dт. t∗

Из соотношения (28) вследствие (27) следует, что a _rr ( r 2 , t ) = 0 .

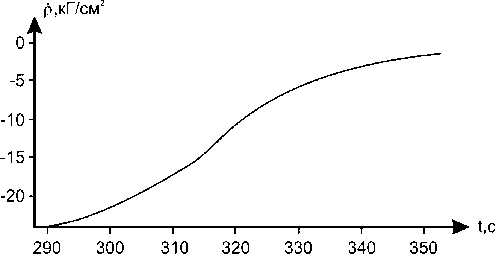
Рис. 4. Давление жидкости на границу формируемой твердой части Q .

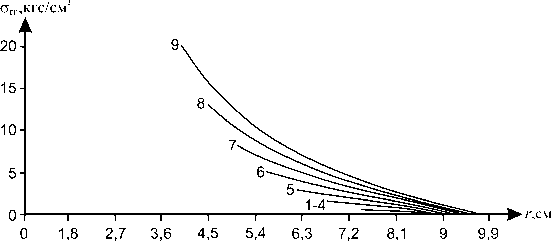
Рис. 2. Динамика окружной радиальной напряжения: Q rr = о _гг ( r, t ); условия на рис. 1.

Заключение

В работе предcтавлена математическая модель объёмного формирования цилиндрического изделия с учетом ненулевой критической глубины конверсии. Рассмотрен метод определения внутренних напряжений формируемого изделия с учетом давления со стороны жидкого слоя на формируемую твердую часть. Приведены и обсуждены результаты численных экспериментов.

Значения параметров задачи: c = 2 . 4 · 10 ² кал/ ( кг · град ); ρ = 1 . 1 · 10 ³ кг/м ³ ; λ 0 = 9 · 10 ^{- 2} кал/ ( м · с · град ); Q p = 1 . 8 · 10 ⁷ кал/м ³ ; Q cr = 3 . 5 · 10 ⁷ кал/м ³ ; k 01 = 5 · 10 ⁵ с ^{- 1} ; k 02 = 2 · 10 ⁴ с ^{- 1} ; U = 1 . 3 · 10 ⁴ кал/моль ; R u = 2 кал/ ( град · моль ); ϵ 1 = 0 . 18; ϵ 2 = 0 . 05; E ^a = 8 . 8 · 10 ³ кал/моль ; ψ = 225 K ; T f = 493 K ; T 0 = 423 K ; R = 0 . 1 м ; R 1 = 0 . 01 м ; h 0 = 0 . 5 · 10 ² м ^{- 1} ; h = 5 · 10 ² м ^{- 1} ; ν = 0 . 33; k 1 = k 2 = - 0 . 01; α 0 = 2 . 5 · 10 ^{- 3} град ^{- 1} ; A = 10 ² сП ; E ^vz = 5 · 10 ³ кал/моль ; E 1 = E = 10 ³ кал/моль ; A 1 = 5 .