Объемные модули газонаполненных материалов

• А.    С. ТЮРЯХИН, кандидат технических наук,

• Е.    В. КИСЕЛЕВ, кандидат технических наук

  1. Две расчетные модели материала. При определении объемного модуля упругости К материалов с большой пористостью — более 50 % от общего объема — возникает потребность учета вли

  
  

  яния величины порового давления р. В предлагаемой расчетной модели за основу примем материал, состоящий из твердой матрицы, с заполненными газом порами (подобие модели Хашина [1]).

  
  

  © В. Д. Черкасов, А. С. Тюряхин, Е. В. Киселев, 2003

Представительная ячейка материала в такой модели представляет собой шарообразную матрицу радиусом Ь, содержащую в своей центральной части сферическую полость радиусом а (рис. 1). Матрица снаружи подвержена действию давления q, а изнутри — действию внутреннего (порового) давления р. Материал матрицы характеризуется упругими константами

€т — Ет/(1 — 2vm) - 3Km, gm = Е/Ц + vm) = 2Gm, где Em и vm — модуль Юнга и коэффициент Пуассона, Кт и Gm — модули объемного сжатия и сдвига.

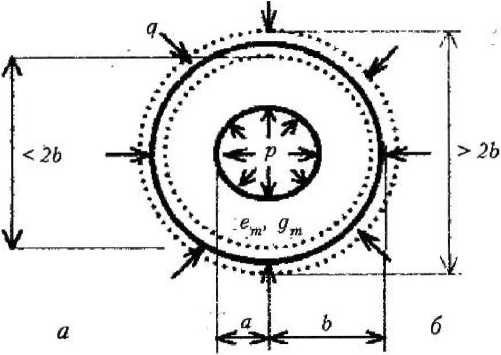
Рис. 1. Два состояния модели, отражающих сжатие (д) или растяжение (б) шара

Из работ [2; 3] следует, что деформация шаровой матрицы с произвольной величиной отношения p/q может иметь два типа состояний, которые характеризуются деформацией сжатия (при уменьшении диаметра 2Ь, см. рис. 1, а) или растяжения (при увеличении диаметра, см. рис. 1, б). Их границей служит условие отсутствия радиальных перемещений в точках наружной поверхности матрицы: м_т(6) = 0. Поскольку и_т0э) - Ь^Г (Ь), то названное условие равносильно равенству нулю тангенциальных деформаций в тех же точках: £™ (6) = 0. Тангенциальные деформации в точках с радиальной координатой г_т определяются согласно [2; 3] выражением

^(r         +             (2)

/и em   m2gm pm где n = (a/bP — коэффициент пористости, m = 1 - n и pm = (r^/bP В точках наружной поверхности матрицы с координатами rm = b и рт = 1 деформации равны

^4bV ^pn"^q + ^{n p}"^q<³> m е_т т 2g _т

С учетом (3) условие е^ (Ь) = 0 примет вид ри -g ] п p-q ^Q тет ™ 2^т

Отсюда после упрощений получим выражение для определения величины предельного отношения [p/q] при заданных значениях и и v_m:

\p/q\= /™< ⁽⁴⁾ п (1 + 9_т )

В (4) и последующих формулах безразмерный параметр упругости материала матрицы, определяемый отношением g — ^^ _ 3^m _ 1 1 ~ Gn ” 2gm 4Gm 2 l-2vm

зависит только от величины коэффициента Пуассона. При значениях п < 1 отношение [p/q] > 1.

Деформация сжатия структурной модели (см. рис. 1, а) реализуется в том случае, когда поровое давление не превышает некоторой предельной величины, т. е. если p/v< [p/q].

Эффективную модель сжатия примем в виде однородного шара, подверженного действию всестороннего давления q (рис. 2, а). В результате получим 1-ю расчетную модель газонаполненного материала, включающую в себя структурную и эффективную модели (см. рис. 1, а и рис. 2, а). Данная модель оправдывает себя при соблюдении условия (6).

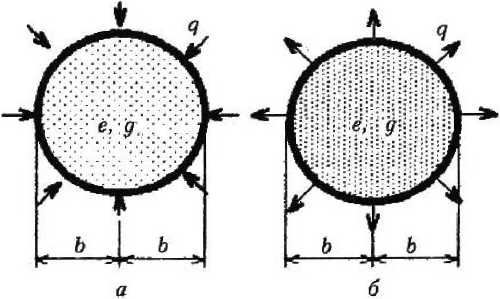
Рис. 2. Эффективные модели, соответствующие 2 расчетным моделям газонаполненного материала: сжатия (д) и растяжения (d)

Условию

P/q > Yp/qA (7) отвечает друга эффективная модель, которая представляет собой такой же однородный шар, но подверженный действию всестороннего растяжения (рис. 2, б). Так образуется 2-я расчетная модель, включающая в себя структурную модель матрицы (см. рис. 1, б) и соответствующую ей эффективную модель (см. рис. 2, б). Следовательно, двум типам состояния одной структурной модели (см. рис. 1) ставятся в эквивалентное соответствие две эффективные модели (см. рис. 2). При этом первая из них отвечает материалам с низким и даже отрицательным (вакуум) поровым давлением, а вторая — материалам с относительно высокими значениями порового давления. Граница, разделяющая две названные области давлений, определяется условиями (6) и (7).

• 2.    Модуль объемного сжатия. В качестве условия эквивалентности для 1-й модели примем равенство перемещений и_т(Ь) наружных точек пустотелой матрицы и перемещений и (Ь) точек эффективной модели. Или, что одно и то же, условие эквивалентности представим в виде равенства деформаций:

E?t(b). (8)

Левая часть условия (8) задается выражением (3). Эффективная модель испытывает однородное сжатие, при котором деформации

8_tW) = -q/e_v (9)

где е5 — эффективный модуль объемного сжатия газонаполненного материала. Выполнив подстановку (3) и (9) в (8), после упрощений получим:

_е.- _     . ^^ __(10)

l + n[0_m -(A + e^p/qA

Для проведения численного анализа преобразуем данное выражение к модулям объемной упругости по формулам е_х = ЗКр е_т = ЗК_т. Газовый «наполнитель» материала будем считать идеальным газом, находящимся под давлением р. Для идеальных же газов гидростатическое давление р эквивалентно модулю объемной упругости газа при любой температуре и, следовательно, р = К_п. Кроме того, для вычислений примем величину внешнего давления q равной величине модуля К„ матрицы. С учетом этого формула (10) в безразмерных величинах примет вид

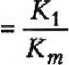
_________™_________ (И)

^п1бт-(^етЖп/ктА

Для последующего сравнения в аналогичном виде представим оценки модулей по Фойгту и по Рейссу [1; 2]:

MF =

Кт Кт

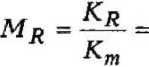
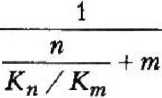
На рис. 3 представлены результаты вычислений эффективных модулей по формулам (11), (12) при п = 0,5 и q - К_т. Графики модулей даны в зависимости от изменения величины p/q = - К_п/К_т. Кривые модуля М j построены для величин 9_т , отвечающих четырем различным значениям коэффициента Пуассона матрицы.

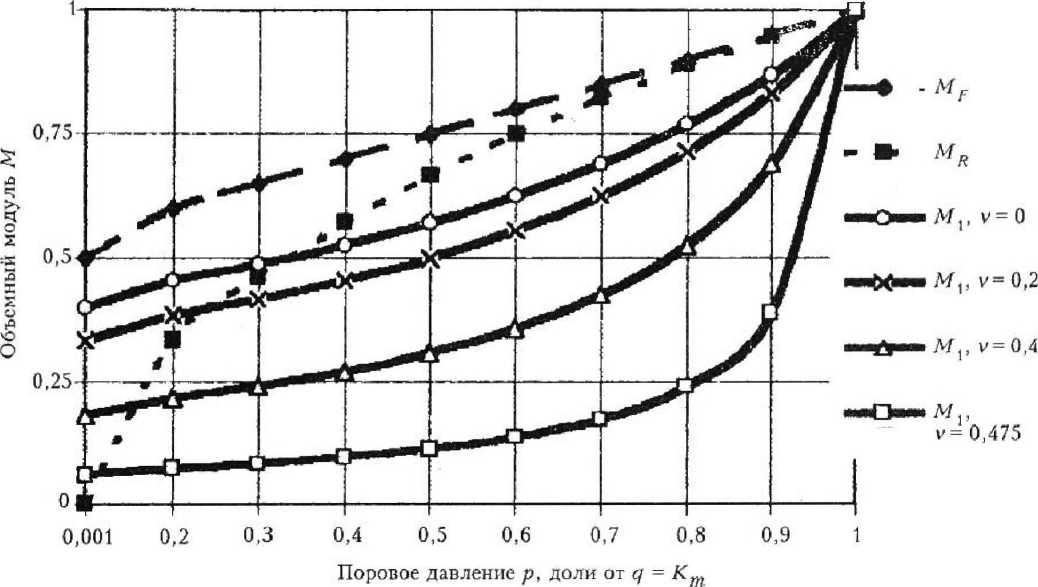
Р и с. 3. Зависимость объемного модуля от величины порового давления

Из рассмотрения кривых следует, что значения эффективных модулей попадают в вилку Хилла (штриховые линии) только при низком поровом давлении в пределах 0 <  p/q <  0,33 (для коэффициента v_m = 0). При значениях v_m > 0 верхний предел данного диапазона существенно сокращается. При 0,33 <  p/q <  < 1 кривые модуля M_t при всех значениях v_m выходят из вилки Хилла и величина Mj становится ниже оценок как по Фойгту, так и по Рейссу.

Применительно к случаю отсутствия порового давления, когда отношение К_п/К_т = 0, выражения (11), (12) упростятся и примут вид:

„ К т

Мл = - = — ,

^т 1 "*" ^т

KF

Мр - —— = т.

MR=^--0.

Кт

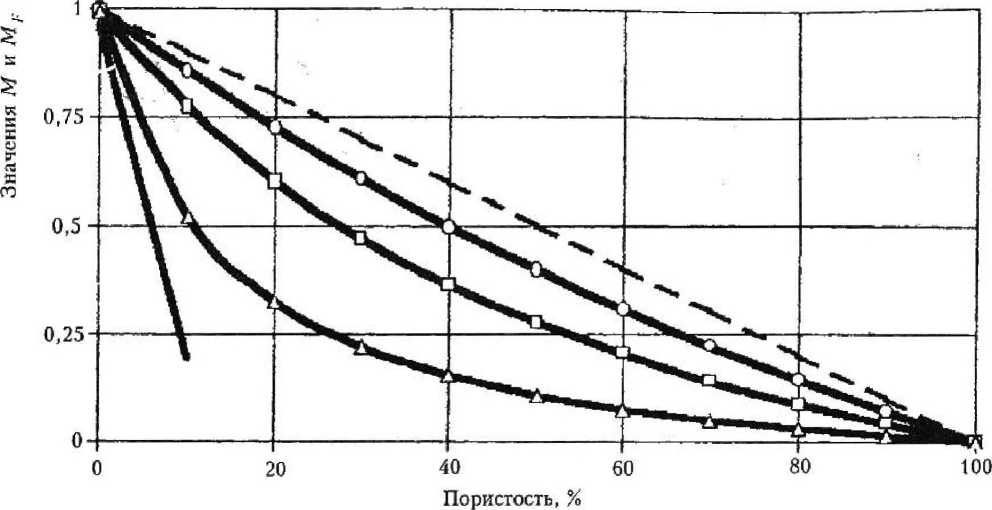
Вид зависимостей (13) показан на рис. 4. Сплошные кривые М^ расположены ниже штриховой линии M_F, т. е. все значения модулей М _х попадают в вилку Хилла.

• 3.    Модуль объемного растяжения. Условие эквивалентности (8) для 2-й расчетной модели сохраняет прежний вид: левая часть задается тем же выражением (3), однако правая часть равенства (8) теперь меняет знак, т. е. деформации эффективной модели (см. рис. 2, б) равны

е£(6) = ^/е2 = const, (14)

где е2 — эффективный модуль объемного растяжения пористого материала. Подставив (3) и (14) в условие (8), получим выражение для модуля объемного растяжения, которое представим в следующем виде:

62 = 9 т х х_______2шр/р_   _ (15)

и<1 + 1/0_т) -(и + 1/ 6_m)q/p

Величина отношения q/p в данном случае ограничивается значением предельного отношения [^/р], определяемого согласно (4) выражением

Vq/p^ =

1         1 + 6_т

—. . ■• = п-----— [p/q]    1 + дб_т

—О— о —о— 0,3 II ti II 0,45 I—HI- I 0,49-- v_m

P ис. 4. Зависимость модуля М_х от пористости при отсутствии порового давления

При пользовании формулой (15), чтобы исключить деформацию сжатия, необходимо соблюдать условие

0 <  q/p < [q/p]. (17)

Анализ выражения (15), аналогичный тому, как это было сделано с (10), показывает, что значения модулей объемного сжатия е_х и растяжения е₂ различны. Особо отметим лишь один характерный случай. Б работе [3] установлено, что если давление q - рп, то матрица (см. рис. 1) испытывает состояние чистого сдвига (сферический сдвиг). Поэтому, приняв q/p = п, из (15) найдем, что е₂ = 2д_т. Отсюда с учетом того, что е₂ = ЗА"2 и д_т = 2G_m, получим: К2 = 4G_m/3. Следовательно, при поровом давлении р = q/n эффективный модуль объемного растяжения К₂ газонаполненного материала численно равен 4/3 от величины модуля сдвига матрицы (при любой пористости материала).

Выводы* Из вышеизложенного следует, что:

• 1)    объемная жесткость газонаполненных материалов характеризуется эффективными модулями объемного сжатия 7<_t и растяжения Х₂> которые различны по

величине и определяются при рассмотрении двух разных расчетных моделей;

• 2)    практическое значение имеет прежде всего модуль сжатия К j, реализуемый в диапазоне давлений 0 <  p/q < 1. Модуль растяжения К^ может быть использован при оценке жесткости газонаполненного материала в процессе его становления (например, отвердевания или полимеризации);

• 3)    применительно к 1-й расчетной модели действует зависимость: чем выше поровое давление, тем жестче материал, и наоборот. Она нелинейна и существенно зависит от величины коэффициента Пуассона;

• 4)    для модуля Х₍ характерны три области значений порового давления: а) низкого давления, при которых значения К । попадают в вилку Хилла; б) средних давлений, когда величина К^ ниже оценки Рейсса; в) высоких давлений, при которых К^ превышает оценку Фойгта. В последнем случае, т. е. в интервале значений 1 <  p/q < [p/q], формула (10) дает неустойчивые результаты, так как при значениях p/q, близких к значениям [р/g], наблюдается сильное вли-

• япие малых изменений p/q на величину К ।;

• 5)    при p/q = 1 все кривые (см. рис. 3) пересекаются в одной точке. Это случай сферического сжатия матрицы, при котором эффективный модуль К_х равен модулю матрицы К_т независимо от величины пористости материала. Оценки Фойгта и Рейсса здесь также совпадают;

• 6)    при p/q < 0 (отрицательное поровое давление, слабый вакуум) кривая с

оценкой по Рейссу вырождается (отрицательные значения). Однако кривые модулей Кч и оценка по Фойгту имеют реальные (положительные) значения, причем К^< K_F;

• 7)    при давлении р = 0 значения K_t попадают в вилку Хилла во всем диапазоне коэффициентов 0m<0,5. При v_m = 0 величина К^ ближе к оценке по Фойгту. В случае, когда, v_m —» 0,5, величина Xj стремится к пределу, совпадающему с оценкой Рейсса.