Обеспечение безопасности распределенных электрических сетей

Впоследнее время участились аварии и неполадки на ЛЭП и подстанциях как в России, так и за рубежом, вызванные техногенными и природными явлениями, а также непрерывным увеличением протяженности электрических сетей. Это обусловливает потребность в их непрерывном мониторинге и разработке оперативных методов обнаружения неисправностей (нестабильностей), вызванных техногенными причинами [1 - 3]. Возможным и, по-видимому, удобным методом определения нестабильности в распределенных электрических сетях является авторегрессионный анализ со скользящим временным окном, ширина которого зависит от длительности интересующего интервала нестабильности. Метод потенциально позволяет обнаружить динамическую нестабильность на ранней стадии развития в любой территориально распределенной электрической цепи, что весьма актуально в приложении к энергетической безопасности.

Сущность авторегрессионного анализа [4] динамической нестабильности в электрических цепях заключается в представлении текущего значения вектора измеряемого сигнала e_t в момент времени t виде ряда:

Xt + ci, X t_, +... + ci n Xtn — e t, (1)

где Xt-1, ..., Xt-n - предыдущие выборки, a1, ..., ak - коэффициенты авторегрессии, так, что полная сумма et представляет собой белый шум с гауссовским распределением по величинам ak Xt-k для нулевого среднего значения. При этом оказывается, что величина отклонения куртозиса измеряемого распределения от нормального распределения (с эффективной шириной кривой, при- близительно равной 2,4) является «хорошим» индикатором ранней стадии развития динамической неустойчивости. Куртозис (kurtosis) или эксцесс – это четвертый центральный момент распределения отклонений от среднего, нормированный дисперсией.

Для проведения авторегрессионного анализа необходимо предварительно строить огибающую наблюдаемого сигнала; для этого обычно используются два метода. Первый - синхронное детектирование и последующая фильтрация (обработка ФНЧ); второй заключается в использовании преобразования Гильберта с последующим определением модуля его разложения в соответствующей комплексной плоскости [5].

Для синхронного детектирования желательно скользящее окно с длиной выборки, равной целому числу периодов исследуемого сигнала промыш-

• ¹    – начальник лаборатории Института химической физики РАН им. Н.Н. Семенова, Москва;

• ²    – ведущий научный сотрудник Института химической физики РАН им. Н.Н. Семенова, Москва;

• ³    – ведущий научный сотрудник ЗАО «Телеформ», Москва.

  26.05.2011 14:41:46

  
  
  

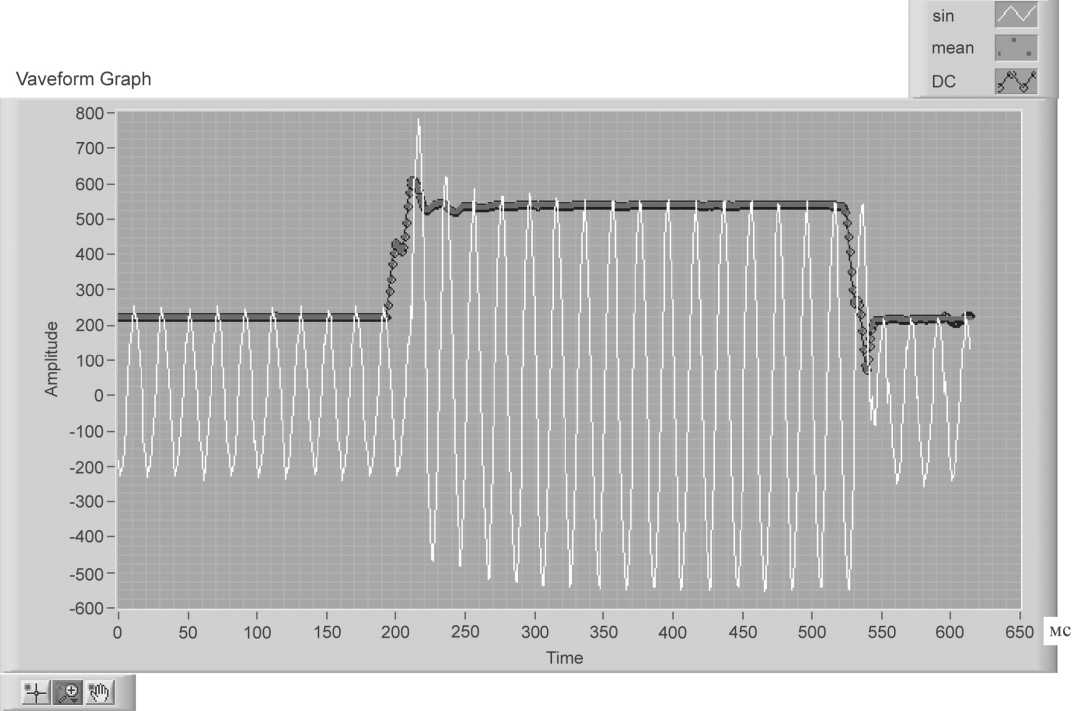
  Рис. 1. Сигнатуры реального сигнала: белая синусоида - с выхода токового трансформатора, синий цвет - огибающая, выделенная синхронным детектированием (и ФНЧ);

  черный цвет - огибающая, выделенная с применением БПФ

  
  

ленной частоты (например, для 4-х периодов – 80 мс), при этом используется вычисление среднего значения за период. Альтернативой является выделение постоянной составляющей с использованием быстрого преобразования Фурье (БПФ). Замена «простого» среднего значения на постоянную составляющую БПФ проводится в целях уменьшения ошибки, обусловленной усреднением. При произвольной выборке с сигнала наблюдаются осцилляции, возникающие, если отсчеты АЦП не попадают строго на максимум входного сигнала или носят случайный характер; они значительно затрудняют проведение авторегрессионного анализа.

Выделение огибающей методом синхронного детектирования имеет два основных недостатка: эффективно подавляется «опорный» сигнал промышленной частоты, при этом сигналы с частотами ниже принципиально не подавляются; при вычислении среднего значения на периоде сигнала теряется информация о быстрых изменениях амплитуды или фазы сигнала. Эксперименты и моделирование показывают, что БПФ-огибающая больше по амплитуде и не имеет специфических осцилляций, отсутствие которых является характерной особенностью данного метода детектирования.

Тем не менее при обработке длительных реализаций огибающие, полученные с использованием БПФ и синхронного детектирования, практически совпадают (т.е. выбор метода некритичен). На рис. 1 изображены огибающие реального сигнала, снятого с токового трансформатора подстанции.

Оценки «правильности» выделения огибающей с помощью преобразования Гильберта производилась с помощью реальных сигналов, полученных с трансформатора напряжения подстанции Оренбургэнерго; фрагменты сигнатур представлены на рис. 2. Для «стационарного» сигнала (рис. 2а) среднее значение огибающей (кривая красного цвета) совпадает с макси- мальными значениями сигнала (кривая белого цвета), что характеризует достаточно высокую точность преобразования. При этом в огибающей присутствуют все гармоники, содержащиеся во входном сигнале. На рис. 2б приведена сигнатура при подаче напряжения на подстанции. Заметим, что в начальный момент включения напряжения происходит сдвиг фазы за счет изменения физических параметров сети; при этом паразитные выбросы отсутствуют.

Для проведения авторегрессионного анализа со скоростью за время одного периода ( Т = 20 мс ) достаточного воспользоваться моделью разложения сигнала 4-го порядка. Процедура расчета коэффициентов авторегрессии a ₁ , ... a _k по (1) сводится к минимизации значений наименьших квадратов предыдущих и последующих величин. Для этого в блок-схему реализации включается расчетный модуль статистического анализа, определяющий куртозис, характеризующий отклонение от нор-

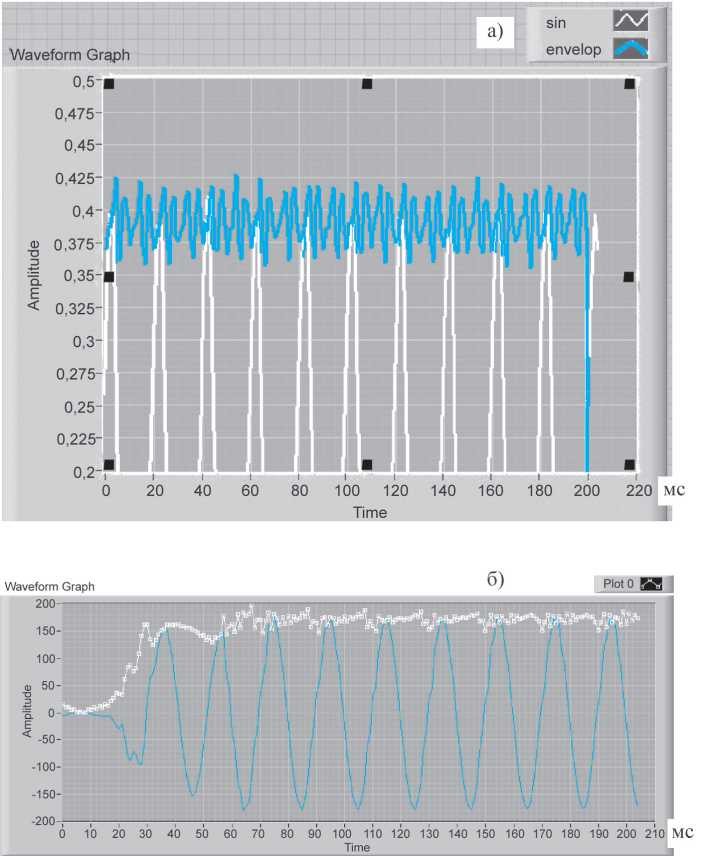
Рис. 2. Сигнатуры сигналов в ЛЭП: а) в «стационарном» режиме;

б) при подаче напряжения; синий цвет - сигнал в линии, белый цвет – огибающая, полученная с помощью преобразования Гильберта

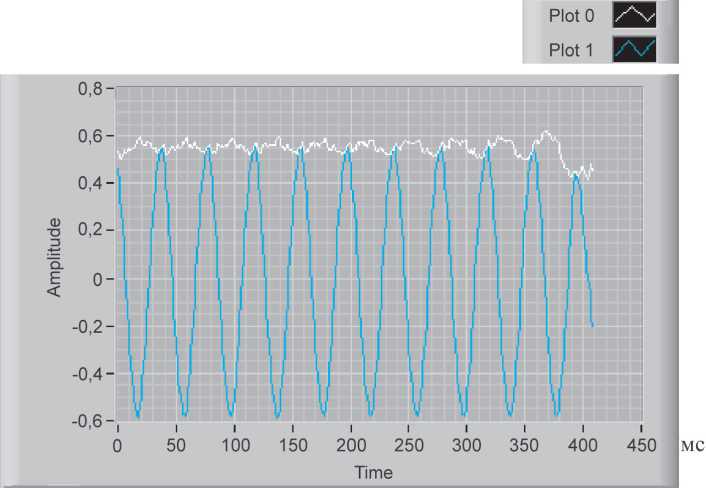
Рис. 3. Сигнатуры кратковременного снижения напряжения сети, сопровождающегося изменением фазы

мального распределения и который представляется в виде

^=Az [^-w], (2) no _{i = 0}

где n - полное число отсчетов входной последовательности Xt ; 〈 X 〉 - ее среднее арифметическое значение, σ - среднеквадратичное отклонение.

Наличие аномалии в принимаемом сигнале приводит к отклонению от модели, которое не обладает нормальным законом распределения. Получено, что если вычисленное по (2) значение куртозиса:

К >2,4 , (3)

то кривая статистического распределения сигнала в сети становится шире кривой нормального распределения, что указывает на наличие динамической нестабильности. Прямой эксперимент показывает, что диапазон изменения куртозиса может достигать значений ~ 100.

Для увеличения скорости расчета параметров авторегрессии использовался метод адаптивного линейного предсказания (АЛП), основанный на предыдущих значениях сигнала (для огибающей напряжения сети). При этом различие между АЛП и другими модельными оценками авторегрессии заключается в том, что адаптивное предсказание можно использовать в реальном масштабе времени.

На рис. 3 приведены сигнатуры сигналов на подстанции в реальной сети, что соответствовало кратковременному снижению напряжения и сопровождались изменением фазы, и было связано с падением электропроводящего предмета (ветки) на высоковольтную ЛЭП. Значение куртозиса, найденное по (2), составило около 12.

Вторым, более сложным случаем, зарегистрированным на подстанции, послужило кратковременное повышение напряжения, связанное с нарушением фазовых сдвигов между векторами напряжений в трехфазной ЛЭП. Обработка процесса привела к куртозису, равному 20,6. В обоих случаях найденные значения K существенно превысили характерную величину 2,4 для нормального распределения по (3).

Проведенные исследования позволи-

Power Line Time Series                                               4~| V^ ^J

1676, 47-

CL |   12001029, 41 —,                 ,                 ,                ।                 !                 ।                 !                 ।                 ,।

0      200     400     600     800    1000    1200    1400    16001799C

Time

Рис. 4. Изменение амплитуды напряжения в ЛЭП ли считать, что предложенный метод раннего обнаружения технологических отклонений является вполне пригодным как при понижении, так и при повышении напряжения сети.

Важным вопросом является возможность раннего обнаружения динамической нестабильности сети. Осциллограмма развития нестабильности типа «раскачивание» представлена на рис. 4, где огибающая сигнала напряжения (измеряемая в вольтах) была получена на одной из подстанций. При этом аварийный сигнал был зафиксирован в момент времени t ≈ 560 c.

Вычисленный соответствующий куртозис для случая рис. 4 равен 50. Этот указывает на прямую возможность использования рассматриваемого авторегрессионного метода для регистрации динамической нестабильности сети, обусловленной периодическим «раскачиванием» амплитуды напря- жения. Заметим, что аналогичная ситуация наблюдается и при периодическом раскачивании частоты, что также приводит к существенному росту куртозиса.

Таким образом, проведенное исследование показало, что для сигнала напряжения с произвольным гармоническим составом и абсолютной величиной модель отклонений стационарного течения процесса носит характер нормального распределения. Вид распределения существенно меняется, если процесс становится нестационарным, вызванным динамической нестабильностью. Разработанный авторегрессионный метод оценки распределения принципиально ориентирован на нестационарные процессы и позволяет выйти за рамки традиционных подходов, основанных на задании жестких пороговых условий при принятии решения.

На основе описанного метода развит алгоритм, позволяющий реализовать универсальный аварийный регистратор, работоспособность и эффективность которого не зависят от типа применяемых датчиков, структуры сигнала, в котором нет необходимости проведения традиционного детектирования сигнала. Это обеспечивает повышение быстродействия как минимум в 4 раза по сравнению со стандартным методом.

На основе полученных результатов разработан прототип прибора для мониторинга состояний электрической сети и раннего обнаружения ее неисправности. Одним из результатов прогнозируется создание системы по организации ремонта или замены оборудования исходя из его фактического состояния. Проведенные испытания прототипа показали его высокую эффективность, возможность получения надежных данных■