Обеспечение равнодолговечности продольной арматуры в железобетонных стержневых конструкциях на стадии проектирования

В концепции расчета железобетонных конструкций минимальные значения толщины защитного слоя установлены из предположения защитного действия на арматуру щелочной среды бетона во все время жизни конструкции. Депассивация арматурной стали при снижении щелочности бетона является результатом взаимодействия конструкций с окружающей кислой агрессивной средой. Агрессивность внешней среды (жидкой или газообразной) — в данном случае условное поня тие, оцениваемое величиной относительного значения потенциала переноса массы вг/60, которое может быть конкретизировано только тогда, когда расматри-вается и оценивается взаимодействие конкретной внешней среды и конкретного бетона.

Расположение продольных рабочих арматурных стержней в принятом традиционном решении армирования прямоугольных (тавровых, двутавровых) сечений показано на рис. 1.

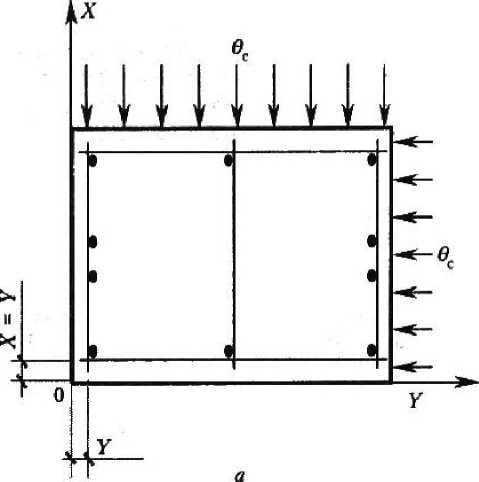
Рис. 1. Расположение арматуры: а — традиционное решение; 6 — решение с равными условиями работы промежуточных и угловых стержней

Толщина защитных слоев бетона как расстояния от взаимно перпендикулярных поверхностей элемента до арматурных стержней принимается равной, то есть Х=¥ Такое расположение арматуры заведомо предполагает неодинаковые условия работы в агрессивных средах для угловых и промежуточных стержней.

Угловые участки поперечного сечения с расположенными в них угловыми арматурными стержнями подвергаются воздействию агрессивной среды с двух взаимно перпендикулярных поверхностей и в теории потенциала переноса массы идеализируются в виде двухгранного угла. Участки поперечного сечения, примыкающие к промежуточным арматурным стержням, удаленные от угловых зон на достаточное расстояние и испытывающие воздействие внешней среды только в одном направлении, идеализируются как полуограниченное тело.

Дифференциальное уравнение потенциала переноса массы, или потенциало-проводпости, по записи аналогично второму закону Фика [1; 3] (без учета тепло- и бародиффузии и при отсутствии внутренних источников или стоков массы):

^2. = ал2», (1) at где 6 — потенциал переноса массы как функция времени и координат; т — время; а — эквивалентный коэффициент потенциалопроводпости.

Решение уравнения (1) при граничных условиях первого рода запишется следующим образом:

• а)    для полуограниченного тела в виде параметра относительной потенциалопроводпости 0_ПТ:

  

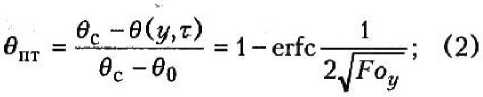
• 6)    для двухгранного угла в виде параметра относительной потенциалопро-водности 0 :

  

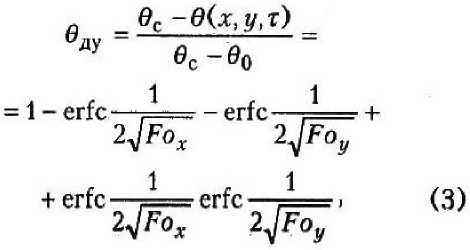
где 0С — потенциал переноса массы окружающей среды; 90 — начальное распределение потенциала массы в теле;

Fo

ат

х '

roy = — — числа Фурье

1 = 1 - erfc—Д

(безразмерное время) соответственно по координате X и по координате У;

или

erf с—т= - 1 - erf—т=, erf 2>jFol        2^0, функция ошибок Гаусса.

Запишем левые части уравнений (2) и (3) следующим образом:

2^

г 1 erfc—,     = 0.

Удовлетворяющим уравнению 1 является решение —^ -.-^ = «, 2^Fo_x

или

Немаловажное практическое значение имеет решение задачи о размещении угловых арматурных стержней таким образом, чтобы они находились приблизительно в одинаковых условиях с промежуточными арматурными стержнями с точки зрения достижимости во времени равных относительных концентраций потенциала переноса массы. Выполнение этого условия, основанного на равенстве правых частей уравнений (4) и (5):

9ПТ

1-^

00 I

Ч ду

1-^

+^, (6)

предполагает равенство параметров потенциалов переноса массы для полуограниченного тела и для двухграпного угла: 0ПТ = 0 Приравнивая правые части уравнений (2) и (3):

Fo_x = — —>0. Полученное решение не х²

вызывает сомнений и справедливо для начального распределения при Fo^O, когда оба тела находятся в равновесном состоянии с окружающей средой.

При воздействии окружающей среды для времени т< 0 и эквивалентном коэффициенте потенциалопроводности а * 0

стремление к нулю числа Fo_x = — х²

возможно лишь при jr —><«. Таким образом, угловые стержни в прямоугольном сечении теоретически будут находиться в одинаковых условиях с промежуточными стержнями в том случае, если двухгранный угол трансформируется в неограниченное тело.

Для практического решения этой задачи следует задаться допустимой величиной расхождения бу в определении относительных параметров потенциала переноса массы для полуограниченного тела 0ПТ и для двухгранного угла 0ду, удовлетворяющей неравенству

1 - erf с —,----= 1 - erfc —,-----

24Foy        2^Fox

- erfc —/ - + erfc — Д — erfc — Д— ^ 274  ²47 ²T4

получаем, что выполнение одновременной достижимости равенства относительных концентраций потенциала переноса массы для полуограниченного тела и для двухгранного угла, имеющих одну общую координату У, возможно при соблюдении условия

^Упт 0ду —---<е». "пт

Левая часть неравенства (10) будет представлять собой не что иное, как

0«т ^ду 0_Пт

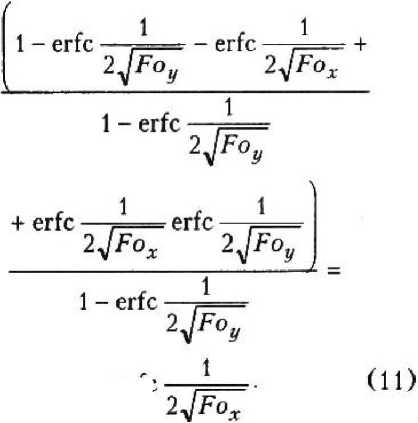
= eric

Зависимость изменения отношения <9„т 5_Ду)/6_Пт ^как функции от Fo_x представлена на рис. 2.

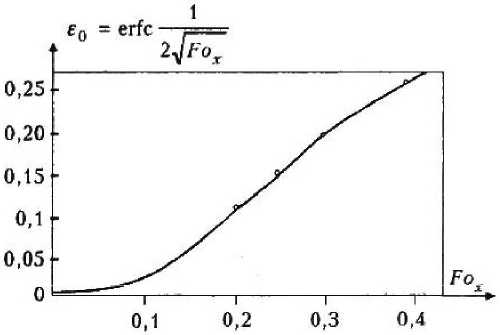
P и с. 2. Изменение величины относительного отклонения Ед в определении параметров потенциала переноса массы для полуограниченного тела и для двухгранного угла в зависимости от числа Фурье

При известных величинах эквивалентного коэффициента потепциалопроводно-сти а, числа Фурье Fo координаты У для полуограниченного тела и допустимого расхождения с₀ в определении параметров потенциалов переноса массы для рассматриваемых сечений значение координаты X для двухгранного угла определяется в следующей последовательности.

В соответствии с рис. 2 определяется число Fox по заданному значению расхождения £0. Затем, учитывая, что массообменные характеристики бетона и время наблюдения для полуограниченного тела и для двухграпиого угла одни и те же, так как они представляют разные зоны одного сечения, из равенства ат = Y2Fo=X2Fox (12)

находим координату X".

Например, при толщине защитного слоя бетона для промежуточных стержней У, числе Fo_y = 1,16 и величине относительного расхождения между значениями параметров потенциала переноса массы полуограниченного тела и двухграпиого угла е₀ = 0,05 = 5 % толщина защитного слоя углового стержня с перпендикулярной стороны должна быть X = У71,16/0, 133 = ЗУ. Здесь £0^=0,133 принято по графику на рис. 2 в зависимости от е₀ = 0,05. При этом значения параметров потенциалов переноса массы, вычисленные по формулам (2) и (5), будут равны: для полуограниченного тела G^Fo, = 1,16) = 0,5; для двухгранного угла 9(Fo - 1,16, Fo_x = 0,133) - 0,475.

Обозначим через Е_а абсолютное отклонение значения параметра потенциала переноса массы полуограниченного тела 0_Пг от параметра двухгранного утла 0_ДУ, которое запишем в виде Е_а = 9_m(,Fo_y) ~ - 9_ду(Ро_у1 Fo_x). Тогда относительное расхождение Е_о и абсолютное отклонение е_а будут связаны между собой следующим уравнением:

ЕО- ^у у «О 0_цту О^ J

Для рассматриваемого примера абсолютное отклонение составит: Е_а = = 9_пт(Ро_у = 1,16) - 0_ду (Fo_y = 1,16, Fo_x = = 0,133) = 0,5 - 0,475 = 0,025, или 2,5 %.

Как видно из формулы (14), при постоянном значении относительного расхождения между параметрами потенциалов переноса массы е0 величина абсолютного отклонения еа уменьшается с ростом параметра потенциала переноса мае- сы 6m(F0y) для полуограниченного тела и, естественно, становится равной нулю при установлении равновесного состояния.

При практическом проектировании железобетонных элементов, связанных при эксплуатации с потенциала переносом массы, правильнее пользоваться не относительным допустимым расхождением Ер, а абсолютным расхождением между параметрами потенциала переноса массы е„, которое, исходя из формул (И) и (14), будет равно

/ х                   1

= Ео^пт \F°y ) = ^ег^^с Т^Г

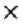
х 1 - erf с

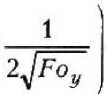
В формуле (15) множитель erfc—'. представляет собой не что 27^х иное, как функцию ошибок. Опа показывает разницу в вычислении параметра потенциала переноса для двухгранного угла вДу, если последний определять по формуле (2) как для полуограниченного тела.

Координата X для углового стержня при заданном абсолютном отклонении между параметрами потенциала переноса ед рассчитывается по формуле (13) при известных координате У и числе Фурье Foy. Количественно Еа как величину ошибки, получаемую при вычислении параметра потенциала переноса массы для двухгранного угла У по формуле (2) как для полуограниченного тела, целесообразно соотнести с величиной доверительной вероятности, принятой при определении нормативной прочности бетона [2]. В соответствии с величиной доверительной вероятности, равной 0,95, значение абсолютного отклонения параметров потенциала переноса массы полу ограниченного тела и двухгранного угла будет равно 0,05, или 5 %. При известных значениях числа Фурье Foy и абсолютного отклонения еа по формуле (2) определяется параметр потенциала переноса мас сы 0ПТ для полуограниченного тела, а затем по формуле (14) — значение относительного расхождения е0. Величина е0 является основанием для определения числа Fo^ по графику на рис. 2.

Для рассмотренного ранее примера при Fo_y =1,16 параметр потенциала переноса массы для полуограниченного тела 6_ni(Fo_y = 1,16) = 0,5. По формуле (14) находим: е₀= Е_а/0_nT(Fo_y- 1,16) = 0,05 : : 0,5 = 0,1. В соответствии с рис. 2 получаем число Фурье: Fo_x = 0,1867 По формуле (13) находим координату X;

X = У 71, 16/0, 1867 = 2,5 У

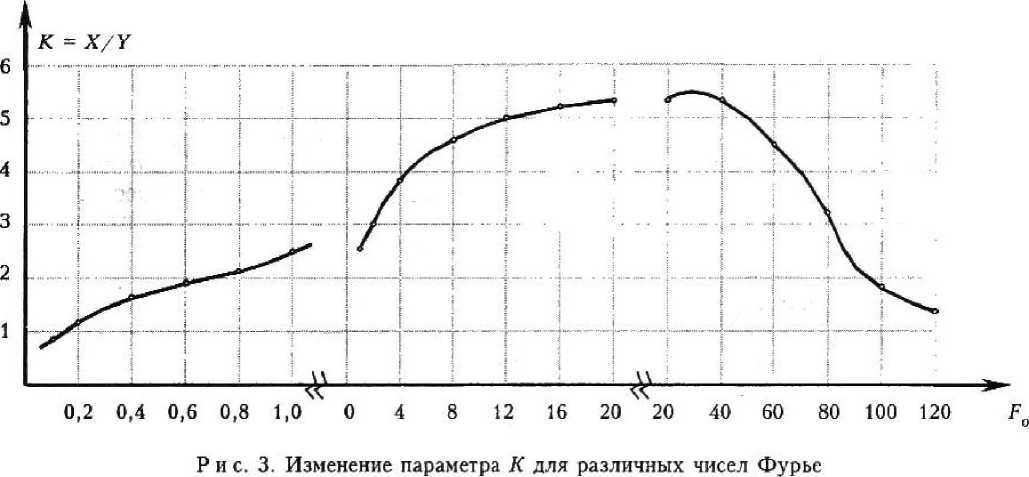
На рис. 3 представлен график, пользование которым позволит, не производя однообразных вычислений по ранее изложенной методике, по известному значению Fo_y = ат/У¹ определить соотношение К = X/Y между координатами X и У для угловых стержней. Как видно из графика, параметр К изменяется во времени неоднозначно. При малых числах Фурье kFo_y < 2) он не превышает величины 2,5 — 3. Для средних значений чисел Фурье, находящихся в пределах FOy = 2...80, параметр К монотонно возрастает до максимального значения, равного 5,5 при Fo.y = 30 и затем начинает монотонно убывать до значения К = 3 при FOy = 80. При больших значениях чисел Фурье kF о у >80) параметр К продолжает убывать.

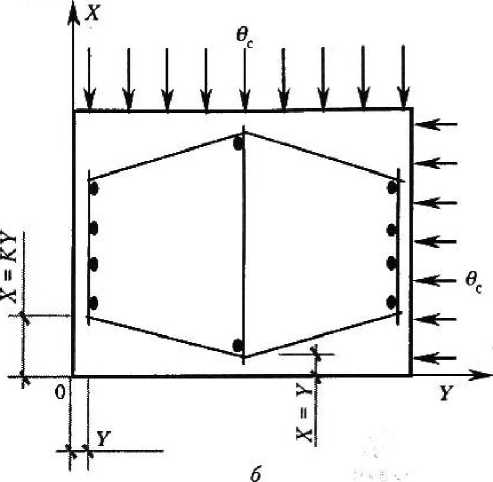
Результаты проведенных исследований показывают, что на внешнее воздействие среды угловые и промежуточные зоны прямоугольных сечений реагируют неоднозначно. Угловые зоны находятся в более жестких условиях по сравнению с промежуточными. Это свойство необходимо учитывать при размещении продольной арматуры при проектировании железобетонных конструкций прямоугольного сечения. При пятипроцентном расхождении между параметрами потенциала переноса массы средних зон, соответствующих при идеализации полубес-конечному телу, и угловых зон, соответствующих двухгранному углу, при общей координате Y для средних и угловых зон значения координаты X для угловых зон определяются из соотношения X = KY Значение параметра К однозначно определяется по графику на рис. 3 как функции числа Foy = ar/Y\ Безразмерное время Foy аккумулирует в себе время эксплуатации, эквивалентный коэффициент потенциалопроводности бетона а и координату Y расположения арматуры в промежуточных зонах.

Правильное размещение продольной арматуры, когда при действии внешней среды значение параметра потенциала переноса массы бетона в зоне промежуточных стержней будет превышать значение параметра потенциала переноса массы бетона в зоне угловых стержней не более чем на 5 %, то есть угловые и промежуточные арматурные стержни будут находиться приблизительно в одинаковых условиях, показано на рис. 1, б.