Обеспечение температурной устойчивости параметров компенсатора эллипсометра

Важной проблемой, непосредственно связанной с точностью эллипсометрических измерений, является температурная неустойчивость параметров компенсатора. В современных эллипсометрах в качестве компенсатора чаще всего используется пластина одноосного кристалла с оптической осью, лежащей в плоскости пластины. Фазовый параметр 8 такого компенсатора описывается приближенной формулой [1]

8 = ²ⁿd ( П е — П о ) ,            (1)

λ где ne = дД^, no = д/ё^ ; d — толщина пластины; X — длина плоской монохроматической электромагнитной волны; ем и е± — главные значения тензора диэлектрической проницаемости eik, отвечающие соответственно оптической оси и двум другим эквивалентным главным осям тензора.

Температурная неустойчивость эллипсометрических результатов при использовании данного компенсатора обусловлена его большой толщиной. На практике обычно используются значения толщин d ~ 1500 - 2000 мкм. При такой толщине температурные колебания показателей преломления n e и n o , проявляющиеся в шестом или седьмом знаке после запятой, а также температурные колебания самой толщины d приводят к заметным изменениям фазового параметра 8 , что существенно сказывается на точности эллипсометрических измерений.

Обычный компенсатор (с оптической осью, лежащей в плоскости пластины), фазовый параметр 8 которого определяется формулой (1), становится термоустойчивым при очень малых толщинах.

Малая толщина может быть достигнута, если пластина одноосного кристалла наклеивается на изотропную стеклянную подложку толщиной 15002000 мкм и затем путем шлифовки и полировки доводится до необходимой малой толщины. При этом изотропная стеклянная подложка становится составной частью компенсатора. Такие компенсаторы, обладающие хорошей термоустойчивостью, существуют. Единственным их недостатком является сложная технология изготовления.

ДВОЙНОЙ КОМПЕНСАТОР

Улучшенным вариантом рассмотренного компенсатора (по температурной устойчивости) является двойной компенсатор [1], состоящий из двух пластин одноосного кристалла, оптические оси которых лежат в плоскости пластин и взаимно перпендикулярны (см. рис. 1).

Для случая, когда "быстрая" ось пластины 2 совпадает с плоскостью падения (соответственно "быстрая" ось пластины 1 перпендикулярна

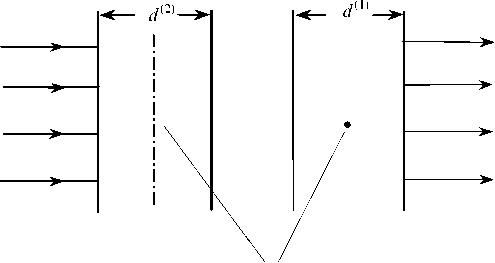
оптические оси

Рис. 1. Двойной компенсатор к плоскости падения), матрицы Джонса пластин имеют следующий вид [1]:

т ( 1 )

L k ~ 1

р (1)

L ^{( 2} ) L_k

~

р(2)

а это означает, как следует из формул (4), существенное снижение температурной зависимости параметров f и 8 двойного компенсатора.

где р ^{( 1 )} = f ^{( 1 )} exp ( - i 8 ^{( 1 )} ) , р ^{( 2 )} = f ^{( 2} ) exp ( - i 8 ^{( 2} ) ) .

Тогда матрица Джонса двойного компенсатора запишется:

КОМПЕНСАТОР С ОПТИЧЕСКОЙ ОСЬЮ, ВЫВЕДЕННОЙ ИЗ ПЛОСКОСТИ ПЛАСТИНЫ ОДНООСНОГО КРИСТАЛЛА

L k = L k L^{2 р ( 1 )}- 0 _р ( 2 )/ _р ( i ) j •       ⁽²⁾

Представим ее в стандартном виде

Lk

ρ

Сравнивая (2) и (3), находим параметр р (f 8 ) двойного компенсатора:

р = Т О = Т О" ^exP ^{( -} i ^{8 (} 2 ) ^{- 8 ( 1 )))}= f ^exP^(- i ⁸ ) ’ ρf

откуда f = fy-    8 = 8(2)- 8(1).          (4)

Ситуация коренным образом изменится [2], если в качестве компенсатора использовать пластину одноосного кристалла с оптической осью, расположенной под углом 6 к нормали пластины (рис. 2).

Электромагнитная волна произвольной поляризации, падающая на такую пластину вдоль ее нормали, внутри пластины распадается на обыкновенную и необыкновенную волны. Необыкновенная волна поляризована в плоскости, образованной оптической осью и нормалью, а обыкновенная поляризована линейно в перпендикулярном к указанной плоскости направлении. Волновые векторы k_e и k ₀ данных волн различны и определяются формулами, полученными из волнового уравнения Френеля [3]:

2π ke =— [n 0 +Vne λ

- n ₀ ) sin² 9 -

Двойной компенсатор всегда представлял интерес в связи с возможностью реализации идеальных значений параметров:

-1. ¹ ( n - n ) ² sin² 9 cos² 9 , 2 n ( 0 )

f = 1 -

8 = 90 ° .               (5)

2π k 0 = T n

Чтобы реализовать ситуацию, когда

^ = 1 ,         8 ^{( 2} )- 8 ^{( 1 )}= 90 ° ,         (6)

необходимо выбирать такие области толщин d ⁽²⁾ и d ⁽¹⁾ ( d ⁽²⁾ >  d ⁽¹⁾ и d ⁽²⁾ = d ⁽¹⁾), для которых

На выходе из пластины между обыкновенной и необыкновенной волнами возникает разность фаз

8 ^{( 2} ) = 180 ° m + 45 ° ,

8 ^{( 1 )} = 8 ^{( 2 )}- 90 ° = 180 ° m - 45 ° ,

где m = 2, 3, 4.

Эти области характеризуются примерно одинаковыми амплитудами осцилляций параметров f ⁽¹⁾ и f <²⁾, 8 ⁽¹⁾ и 8 ⁽²⁾, что почти обеспечивает выполнение условий (6) и, следовательно, условий (5) (см. [1]). По той же причине, а также в связи с малым различием толщин d ⁽²⁾ и d ⁽¹⁾ (это соответствует соотношениям (7)) температурные изменения параметров f ⁽¹⁾ и f <²⁾, 8 ⁽¹⁾ и 8 ⁽²⁾ практически одинаковы,

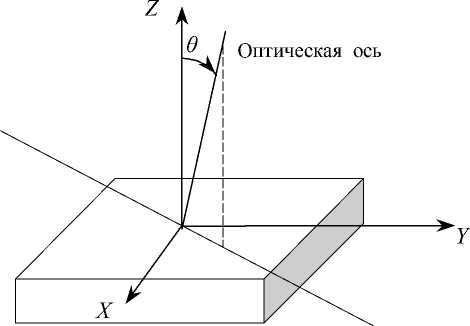
Рис. 2. Компенсатор с оптической осью, выведенной из плоскости пластины одноосного кристалла

5 = ( k_e

- k 0 ) • d = 2^nd- ( П е λ

- n ₀ )sin² 9 ,

которая и представляет собой фазовый параметр пластины одноосного кристалла с произвольной ориентацией оптической оси. Формулу (8) для 8 перепишем в виде, аналогичном формуле (1), т.е. в виде, характерном для обычного компенсатора, у которого оптическая ось лежит в плоскости пластины ( в = 90 , sin e = 1):

2 πd _эф

⁵ = —-—⁽ n e ^{- n} о ) ,             ⁽⁹⁾

λ

где

d эф = d sin² 9 .                     (10)

Минимальное значение d эф , обеспечивающее разность фаз 8 = п / 2 , находится с помощью формулы (9)

) =

эф 4 ( П е - П о )

Считая толщину пластины d заданной в интервале d ~ 1500 - 2000 мкм, найдем с помощью формул (10) и (11) минимальное значение sin e , обеспечивающее разность фаз 8 = п/2 :

^(sin ⁹ Ln = iJ-rT 2 da ( n

λ

e

n 0 У

Рассмотрим для примера пластину кристаллического кварца с параметрами:

d = 1570 мкм, ( n e - n ₀ ) ~ 0 . 01 , X = 0.6328 мкм.

В этом случае (sin 9 )_min = 0.1, т.е. 9 _min = 5 . 5 ° , (d., ) = 15.7 мкм.

эф min

Формулы (1) и (9) аналогичны, но во втором случае d эф на два порядка меньше реальной толщины, а это означает, что температурные колебания фазового параметра 8 снижаются в рассматриваемом случае также на два порядка.

— гораздо большая простота в изготовлении, связанная с низкой чувствительностью (на два порядка меньшей по сравнению с двойным компенсатором) к изменению толщины пластины (изменению толщины в 1 мкм соответствует изменение фазового параметра всего лишь на 3 мин);

• —    простота оптической юстировки (отсутствует необходимость в процедуре по установлению соосности и параллельности пластин);

• —    фазовый параметр каждой из пластин двойного компенсатора составляет 180 m ± 45 ( m — целое число), а в этой области контроль фазового параметра в процессе изготовления пластин оказывается более сложным, чем при 8 ~ 90 ;

— не существует особых требований к точности задания угла в для предлагаемого компенсатора.

Таким образом, использование в качестве компенсатора пластины одноосного кристалла с оптической осью, образующей с нормалью к пластине сравнительно небольшой угол в , может коренным образом изменить ситуацию в эллипсометрии, существенно снизив экспериментальные ошибки, связанные с температурными колебаниями параметров компенсатора. Технология изготовления предложенного термоустойчивого компенсатора разработана на ОАО "Феодосийский приборостроительный завод".