Объяснение аберрации света, световых и электромагнитных опытов по обнаружению “эфирного ветра” с единой точки зрения

Дано объяснение явлению аберрации света и результатам основных опытов по обнаружению “эфирного ветра” при помощи введенного автором статьи постулата увлечения. Предложено провести опыты типа Майкельсона-Морли и Эйхенвальда в космическом корабле, движущемся в околосолнечном пространстве с необходимой для наблюдения эффектов скоростью, при которой они покажут положительные результаты. Вводятся новые определения о системах отсчета. На основе введенных представлений построена теория опыта Физо и выведена формула для угла аберрации света.

Оглавление

• 1.    Физические и координатные системы отсчета.

• 2.    Аберрация света.

• 3.    Опыты Майкельсона-Морли и Саньяка.

• 4.    Опыт Физо.

• 5.    Опыты Эйхенвальда, Троутона и Нобля.

• 6.    Опыт Майкельсона-Гэля.

Литература

1.    Физические и координатные системы отсчета.

Будем считать справедливым следующее утверждение:

Свет,     электромагнитные     волны,     возмущения электромагнитных полей и статические электромагнитные поля макроскопических тел полностью увлекаются произвольно движущимися гравитационными и электромагнитными полями некоторой материальной среды, плотность энергии которых в данной точке пространства превышает плотность энергии полей от других источников.

Назовем это утверждение постулатом увлечения (ПУ).

Совокупность точек пространства, в которых он выполняется, образует физическую систему отсчета (ФСО), относительно которой свет, электромагнитные волны и возмущения электромагнитного поля распространяются по всем направлениям с одинаковой скоростью.

Все остальные инерциальные системы отсчета (ИСО) и неинерциальные (НСО) для процессов, происходящих в ФСО, являются координатными (математическими) системами отсчета (КСО), в которых скорости света, электромагнитных волн и электромагнитных возмущений зависят от величины и направления скорости движения КСО относительно ФСО. Примеры ФСО и КСО будут рассмотрены ниже при описании опыта Физо.

“Эфирный ветер“ можно наблюдать в координатных системах отсчета (КСО), движущихся относительно физических систем отсчета, связанных соответственно с Землей (ФСОЗ), Солнцем (ФСОС) и Галактикой (ФСОГ), одним из известных способов (например, провести в КСО опыт типа Майкельсона-Морли).

И хотя ФСОЗ сама может двигаться в пространстве относительно Солнца, Галактики, Метагалактики и т.д. со сколь угодно большой скоростью, измерить эту скорость оптическими и электромагнитными способами, находясь в ФСОЗ, невозможно в силу ПУ. Поэтому утверждения некоторых исследователей о якобы наблюдаемом движении Земли (“эфирного ветра”) относительно центра Галактики, являются ошибочными.

Реализацией КСО в космическом пространстве является космический корабль, у которого плотность энергии собственного гравитационного поля во много раз меньше плотности энергии внешнего гравитационного поля.

Пусть КСО движется в околосолнечном пространстве с достаточной скоростью на таком расстоянии от Земли, где плотность энергии гравитационного поля Земли будет меньше аналогичной плотности для гравитационного поля Солнца. В этом случае КСО будет двигаться относительно ФСОС и в ней можно обнаружить “эфирный ветер”, т.е. скорость КСО относительно ФСОС.

Точно также, перейдя в область пространства, где плотность энергии гравитационного поля Галактики превысит соответствующую плотность гравитационного поля Солнца, получим ФСОГ. В этой системе КСО сможет обнаружить

“эфирный ветер”, т.е. скорость движения КСО относительно ФСОГ.

Перейти же в ФСО Метагалактики (ФСОМ) аналогичным образом видимо не удастся в силу больших размеров Галактики, поскольку мы должны выйти за пределы Галактики в область, в которой плотность энергии гравитационного поля Галактики окажется меньше плотности энергии гравитационного поля Метагалактики. Если не будет предложено иных способов обнаружения “эфирного ветра”, выходящих за рамки ПУ, то мы так и не узнаем с какой же скоростью Галактика движется относительно Метагалактики.

2.    Аберрация света.

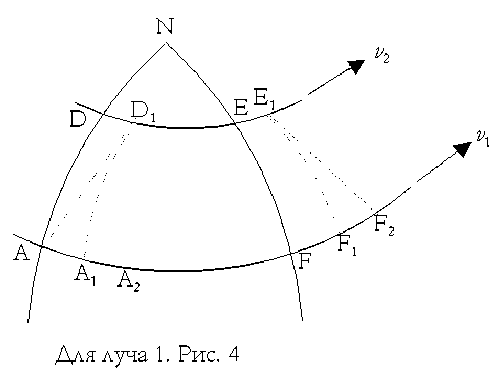
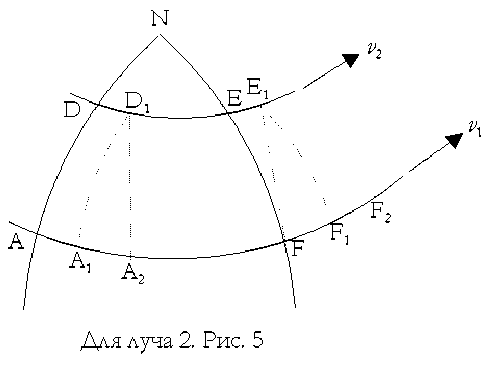
Преломление луча света возникает на границе равенства плотностей энергий гравитационных полей Солнца и Земли. До этой границы в Солнечной системе распространение света происходит относительно гравитационного поля Солнца. При пересечении границы равенства плотностей гравитационных полей свет попадает в более сильное гравитационное поле Земли, относительно которого происходит его дальнейшее распространение. Под лучом света будем понимать пучок фотонов с массой m= E/ c2 , где c – скорость света в вакууме, E – энергия фотонов. На рис. 1 показана схема распространения луча света при аберрации, когда Земля движется в сторону звезды, где S – реальное положение звезды, S′ – наблюдаемое положение звезды, O – начало координат, движущейся вместе с Землей со скоростью v системы отсчета Oxy, расположено на границе равенства плотностей энергий гравитационных полей Земли и Солнца, θ – угол аберрации, α – направление на видимое положение звезды S ′ . Гравитационное поле Земли увлекает свет (его материальную структуру) в направлении скорости v своего движения. Поскольку свет обладает массой m , то его перемещение со скоростью v создает импульс перемещения света pv в направлении этой скорости. И как реакция на такое “принудительное” перемещение, вектор импульса света p поворачивается на угол θ в сторону, противоположную движению Земли как показано на рис. 1. В силу закона сохранения импульса относительно Солнца свет на выходе из увлекающего поля будет распространяться по прежнему направлению SA, т.к. “принудительное” его перемещение закончится и реакция света на это исчезнет.

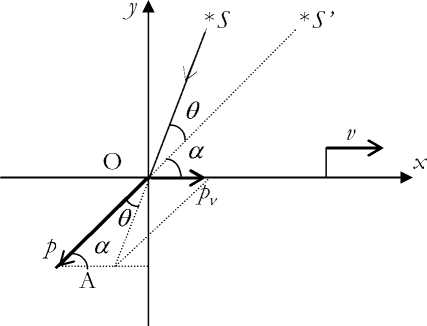
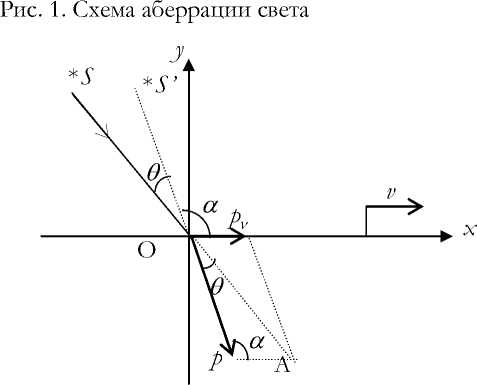
Рис. 2. Схема аберрации света

При увлечении света его энергия и величина импульса не изменяются, поскольку такое перемещение света не происходит вдоль вектора градиента потенциала увлекающего поля. То, что импульс перемещения pv не изменяет импульс и энергию света, находит свое подтверждение в неувеличении энергии фотонов, летящих к Земле от далеких звезд. На своем пути эти фотоны пересекают множество движущихся гравитационных полей, которые, как показывают астрономические наблюдения, не увеличивают энергию увлекаемых ими фотонов. На основании схемы расположения импульсов pv и p (рис. 1) по теореме синусов запишем p. = p

sin9 sin(n — (a + 9))

где P, = |pj = m. , p = |p| = mc — модули импульсов, m = E / c2 — масса фотона. Преобразуем выражение (1)

в = - , (2) c

sin a cos 9 + sin 9 cos a c               в sin a

-------:--------= - ^ tg9 = —----- sin 9           .            1 — в cos a для малых в = 1 получим аберрации света известную элементарную формулу

tg 9 = в sin a .

На рис. 2 показана схема аберрации света при движении Земли в сторону от звезды. Из треугольника импульсов, содержащего pv и p , по теореме синусов получим соотношение, совпадающее с (1). Следовательно формулы (2) и (3) являются общими для этих двух случаев.

Выпишем формулы для аберрации света, полученные в специальной теории относительности (СТО) [1]

sin 5 =

N1 — в   . s, s Р + cos5

-------------sin о , cos о =------------- ,       (4) 1 + в cos 5'                  1 + в cos 5

где углы 5 и 5 связаны с нашими углами a и 9 соотношениями

5 = 180° —(a + 9) , 5 = 180° — a

согласно рис. 1. Подставив (5) в (4) и осуществив элементарные тригонометрические преобразования, для угла аберрации получим выражение

sin al л]1 — в cos a — cos a + в I

tg ⁹ =        ----------------- /------Г ■ 2

cos a — в cos a + ^/1 — в sin a которое при пренебрежении в2 = 1 совпадает с нашей формулой (2). Такое совпадение не случайно, а проистекает оно из того, что как в СТО, так и в данной работе считается, что скорость света в системах отсчета Солнца и Земли одинакова. В данной работе одинаковость скорости света относительно этих двух систем отсчета вытекает из ПУ, а в СТО она следует из постулата о постоянстве скорости света во всех ИСО.

3.    Опыты Майкельсона-Морли и Саньяка.

Объяснение опыта Майкельсона-Морли непосредственно вытекает из самого постулата увлечения (ПУ). Ничего доказывать не надо.

Подтверждением правильности постулата увлечения может служить известный опыт Саньяка [2], в котором свет распространялся с постоянной скоростью относительно гравитационного поля Земли. Плотность энергии гравитационного поля вращающейся платформы в этом опыте во много раз меньше плотности гравитационного поля Земли, вследствие чего согласно ПУ свет будет распространяться с постоянной скоростью по всем направлениям относительно гравитационного поля Земли, а следовательно и относительно самой Земли. И неправильно некоторые утверждают [3], что опыт Саньяка не противоречит СТО, в силу того, что вращающаяся платформа является неинерциальной системой отсчета, которые СТО не рассматривает. Так, например, Лауэ [3] опыт Саньяка рассматривает как оптический аналог опыта Фуко с маятником, признавая тем самым, что скорость света постоянна по всем направлениям относительно Земли.

Для наблюдателя, находящегося на вращающейся платформе, скорость света относительно нее в соответствии с ПУ равна c — v , где v = wR — скорость точек платформы, находящихся на расстоянии R от ее центра, ω – угловая скорость вращения платформы; c – скорость света относительно Земли.

Движение точек вращающейся платформы на ее периферии можно приближенно считать поступательным на небольших интервалах времени, в течение которых свет распространяется при осуществлении опыта. В течение этих коротких промежутков времени движущиеся точки платформы на ее периферии можно рассматривать как локальные ИСО, в которых скорость света согласно второму постулату СТО постоянна по всем направлениям. Вследствие чего время распространения света как по направлению вращения платформы, так и против, будет одинаковым и сдвиг интерференционных полос окажется нулевым. Таким образом СТО приводит к отсутствию эффекта Саньяка вопреки его существованию. СТО вступила в противоречие с опытным фактом и потому должна быть отвергнута. И чем быстрее это будет сделано, тем полезнее для науки.

Почему же сторонники СТО с дьявольским упорством пытаются доказать противоположное? Ответ очевиден. Во-первых, если СТО не объясняет этот эффект со своей точки зрения, то это будет являться свидетельством ее неполноты. Во-вторых, сторонниками СТО руководит не стремление к познанию научной истины, а защита своего авторитета, поскольку они в своих работах использовали СТО как правильную теорию и признать ее ложной для них абсолютно не приемлемо. Точно такие же причины не позволили основателям СТО признать ее ложной после осуществления опыта Саньяка, они пошли на компромисс со своей совестью, тем самым затормозив правильное развитие физики на целое столетие. Только опыт сумеет отрезвить твердолобых приверженцев СТО, их надо ткнуть носом в неоспоримый факт. И такие факты в скором времени появятся. Опровержение СТО станет уроком для всех занимающихся наукой, а для историков и психологов науки появится обширное поле деятельности.

Опыт Майкельсона даст положительный результат, если его провести на космическом корабле (скорость которого порядка скорости орбитального движения Земли), движущемся в околосолнечном пространстве.

В этом случае плотность энергии гравитационного поля Солнца превысит плотность энергии гравитационного поля космического корабля и свет будет распространяться относительно гравитационного поля Солнца с постоянной скоростью по всем направлениям в соответствии с ПУ. Положительные результаты опыта Майкельсона на космическом корабле покажут ошибочность представлений специальной теории относительности.

4.    Опыт Физо.

В неподвижной среде свет имеет скорость v = c / n, где c — скорость света в вакууме, n - показатель преломления среды. Скорость света в среде является переменной величиной, v - это средняя скорость. Взаимодействие света (фотонов) с атомами среды приводит к изменению его скорости и поскольку плотность энергии атомных полей на пути распространения света не является постоянной, то и скорость света на этом пути не постоянна. Свет полностью увлекается движущейся средой на тех ее участках, на которых плотность энергии атомных полей превосходит плотность энергии гравитационного поля Земли. На этих участках свет распространяется относительно среды со средней скоростью v0 . На всех же остальных участках, на которых свет не увлекается движущейся средой, его средняя скорость относительно неподвижной среды равна c0

Пусть свет в неподвижной среде проходит: путь l со скоростью v=c/n, путь l₀ со скоростью v₀ , путь l–l₀ со скоростью c₀ . Время распространения света по всему пути запишем двумя выражениями, которые приравняем

In к l -1               n c

= — + —- ^ 10 = 1—— c    v0      c0                     Co. - 1

v₀

• 1) . Свет распространяется по направлению скорости u движения среды внутри трубы на общем пути длиной 2L. Пусть t₁ – время распространения света в этом направлении. За это время из трубы вытечет столб жидкости длиной l_ж = ut₁ , тогда реальный путь света в среде составит l =2L – ut₁ . При вычислении времени t₁ на этой длине скорость света рассматриваем относительно движущейся

  среды

  
  

10   1 -10   Д 1     1 )    1

t 1 = — +----- = 10---+ ----- v 0   c 0 — u     V v 0   c 0 — u J c 0 — u

Подставив в эту формулу 10 из (7) и 1 = 2L — ut 1, получим t1

2 L | nc₀( c₀— v₀— u ) + cu |

c ( c₀— и )( c₀— v₀) + и | nc₀( c₀— v₀— и ) + cu

• 2) . Свет распространяется против скорости u движения среды на пути длиной 2L. За время t₂ в трубу втечет столб жидкости длиной 1ж=ut2 ^иреальный путь света в жидкости составит 1 = 2L + ut₂. Аналогично, время распространения света в этом направлении

составит

/ /-/

2 =    + I v 0 c 0 + u

= 10

V ^v 0

c₀+ u _;

l

+ c 0 + u

Подставив в эту формулу 1₀ из (7) и 1 = 2L + ut₂, получим

2 Ll nc (c — v + u) — cu I t 2 =                                            1               .          (9)

c (c₀+ u )(c₀— v₀) — u I nc₀(c₀— v₀+ u ) — cu I

Разность времен равна

St =t2 —t1

4Lu (nc0 — c){c0 (c0 — v0 )[n (c0 — v0) + c] — u²(nc0 — c u⁴( nc0 — c )2 + nc0cu³( c0 — c ) + Au²+ c2c²( c0 — v0 )2

где   A = ( ^c0 ^—v0 )[ v0 ( nc0 ^—c )^{2 — c}0 ( n²c^{2 — c2})

Ввиду того, что

u=c, u=c₀ , отбросим в этой формуле члены ~ u² , u³ , u⁴ , тогда

St =

4 ^Luc0 ( nc 0 - c )( c 0 - v 0 )[ n ( c0 - v 0 ) + c ]

^c0 ^c2 ( ^c0 ^-v0 )2

4 Lu n²

c

^v0 ⁿ

1--•--------------- c 0 n + — c0

c

1 -

v₀

c₀

Разность хода лучей составит А = cS t, интерференционная картина сместится на m полос

— > 1 и c₀

В формуле (10) неопределенными являются отношения

• 1    — v0 • c 0 n + — vc

— < 1, множитель ц =>

v c 0

c₀

Коэффициенты с/c₀ и v₀/c₀ в (10) можно определить, измеряя число полос m для двух разных скоростей u течения жидкости в трубах. Используя эти найденные коэффициенты, по формуле (10) определяем смещение полос m для всех других значений скорости u. Результаты этих измерений покажут насколько верна формула (10).

2 ^c

Множитель ц увеличивает значение m, а — > 1 уменьшает его c₀

относительно числа полос, определяемого по формуле Лоренца-

Френеля [4]

4 Lu (n²— 1) m =--------

X c

.

Насколько точны формулы (10) и (11) должны показать опыты типа Физо, проведенные с разными средами, показатели преломления которых сильно различаются между собой.

В опыте Физо те участки движущейся жидкости, на которых происходит полное увлечение света, являются физическими системами отсчета (ФСО). Общая длина этих участков равна l₀ и свет в них распространяется со скоростью v₀ относительно жидкости. Сам прибор вместе с Землей для этих участков является координатной системой отсчета (КСО), относительно которой скорость распространения света является алгебраической суммой

• V 0 + и .

5.    Опыты Эйхенвальда, Троутона и Нобля. 6.    Опыт Майкельсона-Гэля.

Те же участки жидкости общей длиной l – l0 , на которых свет ей не увлекается и распространяется со скоростью с0 относительно прибора (ФСО), являются КСО, а сам прибор вместе с Землей является ФСО. Скорость света относительно жидкости (КСО) равна c о — и .

В опытах Эйхенвальда с заряженным конденсатором предполагалось обнаружить орбитальное движение Земли относительно неподвижного эфира [5]. Их результаты оказались отрицательными. Объяснение отрицательных результатов этих опытов, также как и опыта Майкельсона-Морли, непосредственно вытекает из постулата увлечения (ПУ).

Электрическое поле конденсатора находится в гравитационном поле Земли, являющееся в данном случае физической системой отсчета (ФСО), и в соответствии с ПУ полностью им увлекается. Перемещение электрического поля конденсатора за счет увлечения его гравитационным полем Земли относительно Солнца не обусловлено его собственной скоростью, которая приводит к возникновению магнитного поля, вследствие чего магнитное поле и не появляется.

Тот же опыт, проведенный в околосолнечном пространстве на космическом корабле, даст положительный результат.

Опыт Троутона и Нобля с заряженным конденсатором [5] по обнаружению скорости орбитального движения Земли (“эфирного ветра”) также показал отрицательный результат. Однако этот опыт вызывает недоумение в самой постановке вопроса о его способности что-то заметить. Авторы опыта полагают, что коль скоро заряженный конденсатор обладает электромагнитной энергией и что эта энергия зависит от угла между векторами электрического поля конденсатора и скоростью движения Земли, то на конденсатор должен действовать вращающий момент. Спрашивается, с какой же стати? Что за физическая причина должна вызвать поворот конденсатора? Конденсатор со своим электромагнитным полем является замкнутой системой и под действием только своих внутренних сил он не в состоянии совершить поворот самого себя – типичный пример полевого самодействия, которое нет, нет, да и появляется в некоторых физических проблемах из-за отсутствия их правильного понимания.

В 1904 г. А. Майкельсон предложил идею проведения эксперимента по обнаружению вращения Земли оптическим методом [6], который был осуществлен лишь только в 1925 г. [7]. Опыт показал, что эфир не увлекается вращением Земли.

Положительный результат в опыте Майкельсона-Гэля вызывает серьезные сомнения из–за ошибки, допущенной в расчете величины смещения интерференционных полос.

Воспользуемся описанием теории этого опыта из работы С.И. Вавилова [8]. Схема интерферометра показана на рис. 3.

Плечи интерферометра AF и DE (AF=DE) расположены на широтах ф1 и ф2 ; линейные скорости вращения Земли на них соответственно равны v 1 = Rm cos ф 1 , v2 = Rm cos ф2 , где R - радиус Земли, ω – угловая скорость ее вращения. Для упрощения расчетов было принято, что l1 = AF = 10 cos ф 1 , 12 = DE = 10 cos ф2 , где 10 = Ra . (12)

“При этом условии стороны EF и AD будут направлены по меридиану, перпендикулярно v , поэтому скорость света вдоль этих сторон будет в точности равна с .” – цитата из [8].

Это было бы верно, если бы на этих участках свет полностью увлекался вращением Земли, но теория опыта исходит из предположения о неувлекаемом эфире. На этих участках AD и EF , также как и в опыте Майкельсона-Морли, существует “эфирный ветер” и траектории лучей света 1 и 2 относительно неподвижного эфира наклонены в сторону вращения Земли, как это показано на рисунках 4 и 5. На рис. 4 луч 1 движется по часовой стрелке вдоль пути AD₁E₁F₂A₂ , а на рис. 5 луч 2 движется против часовой стрелки вдоль AFE₁D₁A₂.

На обоих рисунках: N – Северный полюс; вращение Земли слева направо вокруг N; стороны интерферометра AD и EF направлены вдоль меридианов, как и предполагается в расчете.

Луч 1 (рис. 4) проходит расстояние AD1 за время DD1/v2 и E1F2 за время F1F2/v1 , откуда находим суммарное время его движения в плечах AD и EF t1

DD₁  F₁F₂

v₂v₁

Луч 2 (рис. 5) проходит расстояние FE1 за время EE1/v2 и D1A2 за время A1A2/v1 , откуда общее время его движения в плечах FE и DA равно

EE t 2 = —¹ v₂

AA

+ ——2

v₁

.

Так как F₁F₂=A₁A₂ и DD₁=EE₁ при условии, что плечи интерферометра AD и EF равны, то t₁=t₂ из (13) и (14).

Если сторону AD расположить вдоль меридиана, то вторая противоположная сторона EF интерферометра, параллельная AD, не будет направлена вдоль меридиана, так как контур интерферометра является прямоугольным. И в этом случае, как нетрудно убедиться, суммарное время при обходе расстояний AD и EF для каждого из световых лучей 1 и 2 будет одинаковым при том же условии, что AD и EF равны между собой.

Следовательно, принятое в расчете предположение, что стороны AD и EF направлены вдоль соответствующих меридианов, является ненужным и к тому же оно приводит к большой ошибке, которую авторы расчета не углядели.

Приняв в расчете, что стороны AD и EF расположены вдоль меридианов, чему соответствуют формулы из (12), авторы расчета получили для разности времен T обхода лучами 1 и 2 контура интерферометра ADEFA следующее выражение

2       2l₀Rω  ₂₂

^Т = — (l1 v 1 ^-l2v2 ) = ---— ( COs ф 1 ^{- cos}ф2 ) .

cc

После тригонометрических действий над формулой (15) с учетом близости широт ф1 и ф2 друг к другу (ф1 результате) она приобрела следующий вид ф2 = ф в конечном

4lhω

Т = —— sin ф .

c

Исходя из формулы (16), для сдвига интерференционных полос получим следующее выражение

4lhω

А =----sin ф , λc где l = l0 cos ф - средняя длина сторон AF и DE интерферометра.

Если же теперь, исходя из нашего замечания, что предполагать при расчете расположение сторон AD и EF интерферометра вдоль меридианов не нужно, то положив в формуле (15) l₁=l₂=l , получим

2l           2lωR

^T = ~ ( v 1 - v2 )= —Г” (^COs ф 1 - ^COs ф2 ) • cc

После аналогичных преобразований, что и в формуле (15), получим

2lhω

Т = —— sin ф . c

Тогда сдвиг интерференционных полос окажется равным

2lhω

А =     sin ф ,

λc что в 2 раза меньше, чем по формуле (17), используемой экспериментаторами Майкельсоном и Гэлем для сравнения с полученными ими из эксперимента [7] результатами.

Следовательно смещение полос в этом опыте вызвано чем-то иным и его результаты нельзя считать достоверными.

В связи с этим целесообразно было бы провести такой опыт на Северном полюсе, расположив круговой контур кольцевого интерферометра симметрично оси вращения Земли. Это соответствовало бы схеме опыта Саньяка [2], для которого сдвиг интерференционных полос равен

4πr²ω 4Sω

Δ ==,               (21)

λc       λc где S – площадь контура интерферометра, охватываемого проходящими по нему световыми лучами; r – его радиус.