Области сходимости гипергеометрических рядов в теории многообразий Калиби - Яу

Многообразия Калаби – Яу играют большую роль в современной математической физике (см., например, [1]). Они выделяются в классе комплексных аналитических многообразий тем, что их первый класс Черна тривиальный и среди голоморфных дифференциальных форм на них нетривиальными могут быть лишь формы максимальной степени, пространство которых одномерно. Удачные реализации многообразий Кала-би – Яу были получены в виде гиперповерхностей (или полных пересечений) в торических многообразиях [2], в частности во взвешенных проективных пространствах.

Одной из основных задач в данной области является изучение фундаментального периода голоморфной формы максимальной степени на модульном семействе (деформации) фиксированного многообразия Калаби – Яу. Например, если многообразие Калаби – Яу M задано в виде гиперповерхности

M = {У : Po(У) = 0} во    взвешенно-проективном    пространстве

NN

^P ( k ₀, k 1 ,..., k N ) = P k с однородными координатами y = ( y 1 ,..., y_N ), то рассматривается деформация полинома P ₀ ( y )

Рф ( У ) = P0( У ) -Фо У о Ут- yN + ХФвУ в, веВ

В данной статье мы рассмотрим два примера многообразий Калаби – Яу и вычислим области сходимости двойных гипергеометрических рядов, представляющих периоды этих многообразий.

Пример реализации многообразия Калаби – Яу в взвешенно-проективном пространстве. В соответствии с [3] рассмотрим многочлен

Р (У) = У о + У7 У 3 + У 33 + У7 У 4 + у 4, определяющий во взвешенном проективном пространстве P(43,2,2,7,7) гиперповерхность Калаби – Яу. В подходящих координатах x1,x2 , которые мономиально выражаются через модули деформации поверхности, фундаментальный период гиперповерхности представляется рядом Горна

H 1⁽ x 1 , ^x 2 ) =

₌ у       ^Г (⁷ ^ 1 + ³ ^ 2 + 1)      . . 2   _m

71                                x x , ⁽¹⁾

. 1 , > о Г ²( . 1 + 1) Г 2 (2 . 1 + . ₂ + 1) ^{1 2}

где x 1 =ф _о ⁷ , x ₂ =ф 1 / ф о .

Теорема 1 . Граница области сходимости ряда (1) задается параметризацией

0x1 |,|x 21)=0 ^1( q1, q 2)l,l^2(q1, q 2)1), q = Й1 |,| q 2 |)е^+ \{о,} для которой коэффициенты фо и фр параметризуют комплексные структуры многообразия M. Фундаментальный период на многообразии M можно задать интегралом

где ^ 1 ( q 1 , q 2 ) =

^ 2 ⁽ q 1 , q 2 ) =

q 1 ^{3 (} 2 q 1 + q 2^{) 4} ;

⁽⁷ q 1 + ³ q 2⁾⁷ ’

q 2 ⁽2 q 1 + q 2 ^{)2 (7} q 1 ^{+ 3} q 2 ⁾³

Ф о    г dy о ... dy N

( 2п i ) ^{N + 1} {   Р ф

Ф о >  1,

где контур интегрирования представляет собой декартово произведение ( N + 1) окружностей | y j | = 1, j = о, 1, .., N . Как функция на пространстве модулей этот период является гипергеометрической функцией, а именно: представляется рядом Горна, сходящимся для больших значений выделенного модуля ф _о . Процедура аналитического продолжения периода в другие области пространства модулей была описана в [3].

Для доказательства теоремы используется формула Коши – Адамара, формула Стирлинга и формула дополнения Г(z)Г(1 - z) = п / sin nz.

Граница области сходимости ряда (1) задается следующим уравнением:

7 7 | x 1 |³ - 3 3 ■ 7 5 | x 1 |²| x 2 1 2 + 2 2 • 3 3 | x 1 |²| x 2 | -

- 2 4 | x 1 |² + 2 ■ 3 6 ■ 7² | x 1 || x ₂ |⁴ -

- 3 3 ■ 5²| x 1 || x 2 |³ + 2³| x 1 || x 2 |² + 3 9 | x 2 |⁷ -

- 3⁷| x 2 |⁶ + 3 4 | x 2 |⁵ - | x 2 |⁴ = о. (2)

Это уравнение получается исключением пара-q метров q1, q2 (точнее, параметра t: = — ввиду q1

однородности степени нуль параметризации ¥ ( q )) из параметризации Горна - Капранова

I,. । q\(2q i + q 2 ) 4        । q2 (2q i + q 2⁾²

| x l | =                      ,| xl | =                   .

1 ¹    (7 q i + 3 q 2 ) 7      ²    (7 q + 3 q ₂ )³

( -    ) - 17

H 3 ^{( x} 1 , x 2 ⁾⁼ —7^--- ^x

x ^ ------- 7

^{s i} , ^s 2 ^{5 0} ( s 1)( s 2Ц-

I 3        1        1

^Г 1 7 ^s 1 ⁺ 7 ^s 2 ^{+ 1}

-

s 7¹

-

¹ s 2 +4 Г

⁶ V 2 1 1₅

7 ^{s 1}

s^ +

72 7

Отметим, что если в уравнении (2) убрать знаки модуля, то мы получим уравнение сингулярной комплексной кривой для суммы ряда (1).

Область сходимости ряда (1) может быть представлена графически (рис. 1). Параметризация границы области сходимости, указанная в теореме 1, в логарифмической шкале (рис. 2) представляет собой кусок кривой гиперболического типа, асимптоты которой параллельны координатным осям, а вообще на рис. 2 изображена амеба сингулярной кривой для многозначной функции, определенной аналитическим элементом – рядом (1).

x

I I

V x 23 2

s 2

V x 11 2

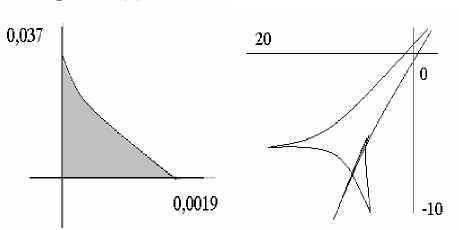
Рис. 1

Ряды (4) и (5) являются аналитическим продолжением фундаментального периода (1) или интеграла (3).

Характерной чертой для ряда (4), равно как и для ряда (1), является то, что аргументами гамма-функций в них являются линейные функции с коэффициентами одного знака при s ₁ и s ₂ . В результате вычислений получается следующая формула параметризации для границы области сходимости ряда (4):

⁽ i x 1 1,1 x 2 1 ) =

/

q ₁

Рис. 2

Ряд (1) допускает представление в виде интеграла Меллина – Барнса [4]

¹    _fr( z ₁) F ( z 2) r ( - 7 z _L-3 z _1±1)

^{( 1}, ² ) ( 2ni ) ^{2 J}F ² ( - z 1 + 1 ) Г ² ( - 2 z 1 - z 2 + 1 )

x ( - x ₁ ) ^{z 1} ( - x ₂ ) ^{z 2} dz ₁ dz ₂ ,             (3)

где у - любая точка из треугольника { те R² : т ₁ >  0, т ₂ >  0,7 т ₁ + 3 т ₂ <  1 } .

Для интеграла (3) существуют три формулы его вычисления в виде рядов из вычетов [4]. Один из этих рядов совпадает с формулой (1), два других выписываются следующим образом:

( - Y ) - 13

H 2 ^{( x} 1 , x 2 ) = "--- у--- ^x

f 2    7 I fl 7 Л n il ^ --52 I г| - s + - s, +1 Ie V3 3 2

^ V 3 ¹ 3 ² 2

^{s ,} ’ ^{s 2 a} ° ( S 1 )( s 2 >Г ² ( s 2 + 1 ) Г ² |- 3 s 1 - 3 s 2 + 2 1

f 1 I ^s 1 p/31

V ^x 2 2

s 2 x

V x ₂ ^7/3 2

3 q 1 ⁺ 3 q 2

13               23 ,

1 1          1 ।

I 1 3 q 1 ⁺ 3 q 2 1

q ₂

f 1      7 2 11      1 I

1 3 q 1 ⁺ 3 q 2 1 1 3 q 1 ⁺ 3 q 2 1

Приведем изображения амебы сингулярной кривой для многозначной функции, определяемой интегралом (3) или рядами (1), (4), (5) в коорди-1 x             x             1

натах t 1 = ^3 , t 2 = —13 и t 1 = ^-7 , t 2 = -777 x ₂           x ₂              x ₁             x ₁

(рис. 3, 4).

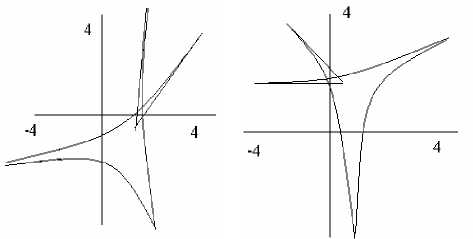
Рис. 3                  Рис. 4

Пример реализации гиперповерхности Ка-лаби – Яу в торическом многообразии . В работе [4] приведена реализация трехмерного многообразия Калаби – Яу в соответствующем ториче-ском многообразии X размерности 4. В координатах y ₁, y ₂, y ₃, y ₄ всюду плотного в X комплексного тора T ⁴ деформация этого многообразия задается нулями полинома

^Р Ф = ^{- 1} + У 1 + ... + У 4 + Ф о ( У 1 У 2 У 3 ) ¹ + Ф 1 ( У 4 ¹ У 1 У 2 )

Там вычислен фундаментальный период в виде гипергеометрического ряда Горна:

.    \-      Г(4 S i + 4 s. + 1)

H 1 ⁽ x 1 , x 2) = E -i"----- 2 2

S 1 ,s 2 > 0 Г 2 ⁽ s 1 + s 2 + 1^{) (} s 1 ! ) ⁽ s 2 ! )

x ₁ ^{s 1} x ₂ ^{s 2} , (6)

где x 1 =ф ₀; x ₂ =ф ₀ Ф 1 . Заметим, что граница области сходимости ряда (6) выписывается в виде

I ^x 1 I ⁺ 1 ^x 2 I - ~ | ^x 1 I -

• . . . . 2 .            .            1

• - 2| x | - | x 2 | - — | x 2 I + — = 0.

44        48

Область сходимости ряда (6) представим графически (рис. 5), а также изобразим амебу для сингулярного множества этого ряда (рис. 6), причем затемненная компонента дополнения этой амебы и есть область сходимости ряда (6) в логарифмических координатах.

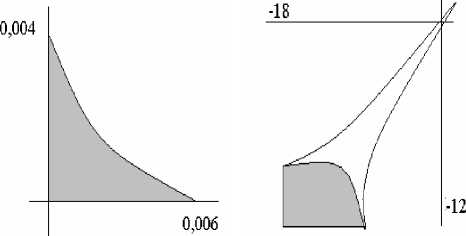
Рис. 5                     Рис. 6

Таким образом, общий результат Горна об областях сходимости гипергеометрических рядов не дает полной информации о рядах, встречающихся во многих приложениях, в частности в теории суперструн. Это ряды, представляющие фундаментальные периоды на многообразиях Калаби – Яу. В данной статье рассмотрены именно такие примеры многообразий Калаби – Яу и вычислены их области сходимости.