Обнаружение аномалий на гиперспектральных изображениях

Одной из распространённых задач обработки цифровых гиперспектральных изображений является обнаружение аномалий. Существуют совершенно различные определения понятия «аномалия», используемые в различных прикладных задачах и зависящие от специфики данных [1]. Применительно к задачам анализа гиперспектральных изображений под аномалией обычно понимают пространственную область небольшого размера, спектральное описание которой имеет существенное отличие от её окрестности [2–4].

Один из первых алгоритмов обнаружения аномалий, который был предложен для обработки гиперспектральных изображений в работе [5], – это RX-алгоритм (RX detector), получивший широкое распространение и названный в честь его авторов – I.S. Reed and X.Yu. Величина «аномальности», вычисляемая в RXD-алгоритме, представляет собой расстояние Махалонобиса до среднего значения спектральных сигнатур на изображении. Таким образом, в качестве аномалии выступают наиболее удалённые от среднего значения сигнатуры с учётом корреляционных зависимостей между спектральными каналами. Этот первый алгоритм демонстрировал хорошие результаты для изображений с «простым» фоном, представимым единственной сигнатурой, но для более сложных задач оказался неэффективным. Данный факт, а также возможность разного формализованного определения данного выше понятия «аномалия» привели к появлению большого числа как модификаций предложенного RX-алгоритма, так и совершенно новых решений. Некоторые возможные классификации таких решений по различным критериям с достаточно полными списками соответствующих публикаций представлены, например, в монографиях [3–4] и обзорных работах [6–10]. А примерами работ с модификацией известного RX-алгоритма и разработками новых алгоритмов являются работы соответственно [11] и [12–15].

Следуя классификации, данной в работах [7–8], алгоритмы обнаружения аномалий можно подразделить на подгруппы по используемым в них подходам:

– алгоритмы, использующие переход к сокращённому описанию (Subspace Methods), для которого обычно используется метод главных компонент, или метод сингулярного разложения. Отличительная особенность этого класса методов – глобальное преобра- зование, применяемое для всех отсчётов гиперспектрального изображения;

– локальные алгоритмы, отличительной особенностью которых является использование отсчётов локальной окрестности для оценки «фона»;

– алгоритмы, использующие предварительную сегментацию и позволяющие осуществить предварительное разделение изображения на «фоновые» области. Внутри последних и производится обнаружение аномалий.

Указанные выше подходы используются в конкретных алгоритмах и отдельно, и совместно. При этом сами алгоритмы на заключительном этапе могут и использовать алгоритм RXD, и не использовать. Этот факт, а также постоянное появление новых алгоритмов, которые не попадают в обозначенную классификационную схему (например, алгоритмы на основе графов [12] или «топологические» алгоритмы [15]), говорит в целом о достаточной условности такой классификации.

Предлагаемые в настоящей работе новые алгоритмы отличаются своими подходами к определению величины «аномальности», базируясь на различных математических моделях изображения и/или используя различные аспекты этого понятия. Так, первый из алгоритмов – алгоритм пространственно-спектрального рассогласования – предполагает, что изображение описывается моделью стационарного случайного поля и использует в качестве величины «аномальности» некоторой области величину пространственноспектрального рассогласования его с окрестностью.

Второй алгоритм – алгоритм адаптивного спектрального рассогласования – под величиной «аномальности» понимает величину, пропорциональную величине ошибки, возникающей при представлении отсчётов анализируемого фрагмента через отсчёты его окрестности. Данный алгоритм разрабатывается в двух вариантах – без использования и с использованием нормирования гиперспектральных отсчётов.

Учитывая то, что величина «аномальности» в обоих алгоритмах определяется как величина спектрального рассогласования, ниже они объединены в одну группу – группу алгоритмов спектрального рассогласования . Следуя данной выше классификации, оба эти алгоритма можно отнести к группе локальных алгоритмов.

Третий, заключительный, алгоритм – вероятностный алгоритм обнаружения аномалий – использует квантование сигнатур изображения и вычисление хеш-значений квантованных векторов для построения гистограммы частот появления гиперспектральных отсчётов . Вероятность сигнатуры квантованного изображения определяет величину «аномальности» точки изображения: наименее вероятные точки рассматриваются в качестве аномалий. Таким образом, в последнем алгоритме к аномалиям относятся уникальные спектральные сигнатуры на изображении, что наиболее точно соответствует данному в начале работы классическому понятию «аномалии». Возвращаясь к данной выше классификации, следует отметить, что, хотя этот алгоритм является глобальным, он в общем случае не требует перехода к сокращённому описанию. Данный факт позволяет говорить о новом решении, не попадающем в принятую классификацию большинства существующих алгоритмов .

Все разрабатываемые в работе алгоритмы сравниваются с широко используемым RХD-алгоритмом (с глобальной и локальной версией), показано преимущество предложенных алгоритмов на ряде примеров обнаружения аномалий.

Алгоритмы спектрального рассогласования

Алгоритмы спектрального рассогласования используют общую схему расчёта величины «аномальности», c вычислениями в «скользящем окне» [16]. Для этого выбираются два окна обработки, первое из которых – «внутреннее» – интерпретируется как область потенциальной аномалии, а второе – «внешнее» – как окрестность этой потенциальной аномалии (отсчёты «внутреннего» окна не попадают во множество отсчётов «внешнего»). Указанная пара окон занимает последовательно все возможные положения в плоскости изображения (например, в режиме построчно-постолбцовой развёртки), и для каждого их расположения ( n ₁, n ₂), соответствующего текущему положению их центрального отсчёта, рассчитывается величина «аномальности». Величина «аномальности» для области (внутреннего окна) может быть получена путём агрегации значений «аномальности» окна. Заметим, что указанная агрегация может быть выполнена различными способами (сумма попиксельных значений, их минимум, их максимум, их медиана и т. п.).

Для удобства введём следующие обозначения отсчётов «внутреннего» и «внешнего» окна (см. рис. 1):

– I ( n 1 , n 2 ) – множество индексов отсчётов «внутреннего» (малого) окна (области потенциальной аномалии), способ введения упорядочивания отсчётов не имеет значения;

– J ( n ₁, n ₂) – множество индексов отсчётов «внешнего» (большого) окна (окрестность области потенциальной аномалии), способ введения упорядочивания отсчётов не имеет значения.

Обозначим также VV , i е I ( n₁, n 2 ) - значения гиперспектральных отсчётов из множества I ( n 1 , n 2 ), а Vj, j е J ( n₁, n 2 ) - гиперспектральных отсчётов из множества J ( n 1 , n 2 ) .

n 2

n 1

О	о	о о о о о о о
о	о	о о о о о :о о
о	о	О Ю О О О ;О_О.
о	о	о |о • о -оТб о
о	о	о 1о о о об о
о	о	о о о о о:о о
о	о	О О С) о о о о

J(n 1 ,n 2 )

Рис.1. Иллюстрация к определению множеств отсчётов внутри окна обработки

I(n 1 ,n 2 )

Величину спектрального рассогласования ε²( n ₁, n ₂) гиперспектрального изображения в позиции ( n ₁, n ₂) можно определить как ошибку представления гиперспектральных отсчётов из множества I ( n 1 , n 2 ) через отсчёты множества J ( n 1 , n 2 ):

г ² ( n_p n ₂ ) =

V - £ ai (ni, n2 ) Vj j е J ( n1,n 2 )

где K – некоторая норма (в работе используется L 2 ), а α ij ( n 1 , n 2 ) – неизвестные коэффициенты представления. В зависимости от способа определе-ния/задания этих коэффициентов можно рассмотреть две ситуации, приводящие к двум принципиально различным алгоритмам.

В первой ситуации коэффициенты полагаются постоянными на всём изображении (но неизвестными и зависящими от изображения), то есть считаем, что выполняется условие:

a ij ( n 1 , n 2 ) = a ij , i е I ( n₁, n 2 ) , j е J ( n₁, n 2 ) .

Такое определение коэффициентов соответствует рассмотрению изображения как случайного стационарного поля, для которого наибольшие ошибки (1) возникают в местах существенного нарушения «cта-ционарности».

Во второй ситуации выражение (1) используется напрямую. В этом случае речь идёт о возможности представления конкретного отсчёта «внутреннего» окна через отсчёты окна «внешнего»: в тех случаях, когда такое представление сделать с малой величиной рассогласования не удаётся, соответствующий отсчёт (или область) интерпретируется как аномалия.

Ниже рассмотрены оба алгоритма и указаны способы расчёта указанных коэффициентов.

Алгоритм пространственно-спектрального рассогласования

Для алгоритма пространственно-спектрального рассогласования коэффициенты α _ij ( n ₁, n ₂) рассматриваются как постоянные для изображения величины α _ij . Определение этих коэффициентов производится из условия минимума суммарного среднеквадратического отклонения:

г ² = £ г ² ( n i , n 2 ) ,

( ⁿ 1 . ⁿ 2 )

где e2 (ni,n2) =1 E г2 (npn2) =

² i ^e I ( ⁿ 1 . ⁿ 2 )

1 fY

= 2 E V - E ajvj.

2 ie I ( n1, n 2 ) ^       je J ( nl, n 2 ),

Коэффициенты могут быть получены из следующей системы линейных алгебраических уравнений:

E v^T ( n l , n 2 ) vk ( n l , n 2 ) =

( n 1 , n 2 )

J -1

= E “kj E vT ( n1, n2 ) vj ( n1, n2 )’ j = 0       ( n1, n 2 )

где v_k ( n 1 ,n ₂) e I ( n 1 ,n ₂) и k =0.. I -1, v t ( n 1 ,n ₂) e J ( n 1 ,n ₂) и t =0.. J -1.

При рассчитанных коэффициентах α ij величину «аномальности» для области, как было указано выше, можно определить следующим способом:

f

£ (n1, n2 ) = Aggregate v - E “i/vj , ie I (n1, n2) (      je J~ n 2)       J где в качестве функции Aggregate могут выступать любые отображения вида Aggregate: R I ^ R. При- мерами таких функций являются: полусумма значений, приводящая к величине рассогласования (2), минимум, максимум, медиана и др.

Алгоритм адаптивного спектрального рассогласования

Для алгоритма адаптивного спектрального рассогласования коэффициенты αij(n1,n2) полагаются различными для каждого возможного положения окон (n1,n2). Способ нахождения этих коэффициентов заключается в использовании ортогонального проеци- рования конкретного вектора vi внутреннего окна на линейную оболочку (линейное замыкание) векторов внешнего окна [17] и получении его проекции vˆi . В результате ошибка (1) будет иметь вид:

^e 2 ( ⁿ 1 , ⁿ 2 ) = || ^v JГ^-| v i ( ⁿ 1 , ⁿ 2)|| ’ i ^e I ( ⁿ 1 , ⁿ 2 ) ’       ⁽³⁾

где v , ( n 1 , n ₂ ) = P²n ¹ ’ ^{n 2} ) v i - проекция вектора-отсчёта v i из области I ( n 1 , n 2 ) на множество векторов области { v } 2.

i ^Jij ^e J ( ⁿ 1 , n 2 )

Оператор проектирования (проектор) P * n ¹ ’ ^{n 2} ) получается из условия наименьшей среднеквадратичной ошибки представления вектора-отсчёта v _i отсчётами из J ( n 1 , n 2 ) [17]:

Причём a = ( V ^T V ) V T . Поскольку отсчёты J ( n 1 , n ₂) могут быть линейно зависимы между собой, при вычислении проектора можно использовать либо предварительный отбор подмножества линейно независимых векторов, либо регуляризацию. Регуляризованный проектор, использованный в работе, имеет вид:

P±(n1’n2) = V(VTV + PI)-1 VT, где β>0 – параметр регуляризации, I – единичная матрица.

Полная величина спектрального рассогласования для заданного отсчёта задаётся выражением:

£2 (n1, n2) = Aggregate (e2 (n1, n2)), ie I ( n1’ n2 )

где в качестве функции Aggregate могут, как и выше, выступать различные отображения.

Дополнительная модификация алгоритма адаптив- ного спектрального рассогласования заключается в предварительной нормировке всех гиперспектральных отсчётов изображения так, чтобы выполнялось условие

I v ( n 1 , n 2 )|| = 1.

В этом случае величина ошибки (3) может быть представлена в виде e2 (n1, n2) = 1 - cos2 (v, v (n1, n2)) =

= sin ² ( v i , v ². ( n 1 , n ₂ ) ) , i e I ( n 1 , n ₂ ) ,

где синус (или косинус) вычисляется для угла, образованного исходным вектором и его проекцией на подпространство, формируемое векторами «внешнего» окна (их линейного замыкания). Очевидно, данная величина однозначно (и монотонно) зависит от указанного угла.

Вероятностный алгоритм обнаружения аномалий

Пусть v ( n 1 , n ₂ ) - отсчёт-вектор гиперспектрального изображения, содержащий информацию о спектральной сигнатуре соответствующего отсчёта изображения. Заметим, что в качестве компонент v могут выступать как исходные значения гиперспектрального вектора, так и коэффициенты разложения такого гиперспектрального вектора по предварительно найденным спектральным сигнатурам, а также собственно ошибка такого представления. Пусть далее число компонент вектора – n .

Введём величину K – число уровней квантования каждого компонента вектора v . Тогда каждый вектор v на изображении даёт квантованный вектор q = ( q 0 Q 1 K Q n -1 ) ^T , где q j -e { 0,..., K - 1 } .

Тогда в общем случае таблица возможных квантованных значений вектора q имеет размер Kn. Набор вероятностей P (q) для каждой возможной ячейки со значениями (q0 q1 ... qn 1)T образует вероятностное распределение функции яркости гиперспектрального изображения. Поскольку Kn может быть очень боль- шим (число каналов обычных гиперспектральных изображений исчисляется сотнями), то при большом числе анализируемых каналов из-за ограниченности размеров таблицы предлагается использовать хеширование [18], т.е. расчёт для каждого значения (q0 q1 … qn-1)T некоторого целочисленного представления. Тогда вероятностное распределение (или, на практике, гистограмма, эмпирическое распределение) считается для хеш-значения отсчётов гиперспектрального изображения. В настоящей работе в качестве функции хеширования использу- ется следующая:

n -1

/ ( q ) = Z qK mod N , i =0

где N – некоторое большое число, определяемое исходя из доступных размеров хеш-таблицы, mod – операция деления по модулю. Хеширование позволяет организовать простой механизм адресации уникальных значений квантованного отсчёта при расчёте гистограммы.

Пусть I(n1,n2) – множество отсчётов внутри окна обработки, {q, }„i(^,n2)

– множество их квантованных представлений. Результатом для конкретного положения окна является величина:

P ( ^, n 2 ) = ^{1 -} min P ( qi) .                         ⁽⁵⁾

i e I ( n 1 , n 2 )

В выражении (5), аналогично предшествующим двум алгоритмам, помимо минимума могут быть использованы другие агрегирующие функции: максимум вероятности в окне, медиана и др.

Экспериментальное исследование алгоритмов спектрального рассогласования

Для исследований алгоритмов спектрального рассогласования использовались синтезированные тестовые гиперспектральные изображения размером 256×256 со 100 каналами, которым соответствовали длины волн от 0,8 до 2,5 мкм с шагом 0,017. Изображения формировались как линейная комбинация четырёх «фоновых» сигнатур (ACTINOLITE_AM3000, ILLITE_IL101, SEPIOLITE_SEP3101, BUDDINGTONITE_NHB2301) и двух «аномальных» (HEMATITE_FE2602, SIDERITE_COS2002), взятых из библиотеки IGCP-264 Library - CSES Beckman Spectrometer [10]. Коэффициенты смешивания сигнатур и фона и аномалии задавались как стационарные случайные поля с биэкспоненциальными корреляционными функциями. Исследование производилось для трёх синтезированных изображений (PIC-1, PIC-2 и PIC-3) с коэффициентами корреляции p соответственно 0,999, 0,98 и 0,45. Сумма коэффициентов сигнатур в каждом отсчёте была равна единице, коэффициенты неотрицательны [2–4]. Набор аномалий, встроенных в изображение, включал в себя площадки размерами 7×7, 5×5 и 3×3. Примеры тестовых изображений с внедрёнными аномалиями приведены на рис. 2.

Первые два изображения использовались для сравнения результатов работы с известными модификациями RXD-алгоритма (глобальная и локальная, снижение размерности не производилось). Первое изображение соответствовало простой ситуации с практически неизменным фоновым полем (аналог од- ной сигнатуры), в то время как второе – с изменяе-

Для сравнения алгоритмов был проведён следующий эксперимент. В каждый канал тестового изображения добавлялся некоррелированный аддитивный шум с нормальным законом распределения и нулевым средним. Зашумлённые изображения обрабатывались независимо RXD-алгоритмом (двумя указанными выше модификациями) и предложенным алгоритмом пространственно-спектрального рассогласования с параметрами окон 3×3 и 5×5. Результат обработки представлен на рис. 3 и 4 для отношений сиг-нал/шум 1000, 100 и 10 соответственно.

в) отношение сигнал/шум 10

Рис. 3. Результаты для тестового изображения PIC-1 с различным отношением сигнал/шум. Слева направо: метод спектрального рассогласования; RXD-алгоритм

(глобальный);RXD-алгоритм (локальный, окно 5×5)

Более тёмные отсчёты соответствуют б о льшим значениям величины рассогласования и, как следствие, «аномальности».

Чтобы избежать неустойчивости в работе RXD-алгоритма c изображением PIC-1, выполнялось преобразование исходного изображения методом главных компонент перед его применением. На рис. 3 представлены результаты RXD-алгоритма и его модификации для первых двух главных компонент изображения PIC-1. Метод спектрального рассогласования применения метода главных компонент не требует.

Из представленных на рис. 4 результатов видно, что метод пространственно-спектрального рассогласования обладает высокой помехоустойчивостью и обнаруживает аномалии существенно лучше, чем любая из модификаций RXD-алгоритма в случае со сложным фоном (изображение PIC-2).

с различным отношением сигнал/шум. Слева направо:

метод спектрального рассогласования; RXD-алгоритм (глобальный); RXD-алгоритм (локальный, окно 5×5) Влияние на результат выбора размеров «внутреннего» и «внешнего» окна хорошо видно в эксперименте с изображением PIC-3. На рис. 5 показан результат обработки методом   пространственно спектрального рассогласования в случае с размерами 3×3 и 5×5, 5×5 и 7×7, 7×7 и 9×9 соответственно. Как видно, аномалии большего размера лучше обнаруживаются с большим размером окна.

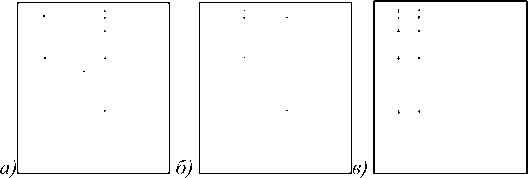
Рис.5. Результаты обработки изображения PIC-3 алгоритмом пространственно-спектрального рассогласования с параметрами размеров внутренней и внешней областей соответственно:

а) 3×3 и 5×5; б) 5×5 и 7×7, в) 7×7 и 9×9

Пример работы алгоритма адаптивного спектрального рассогласования для изображения PIC-1 с соотношением сигнал/шум 100 в каждом канале представлен на рис. 6. В качестве параметра регуляризации использовалось значение 0,01λ_max, где λ_max – максимальное собственное значение матрицы V ^T V .

( П 1 , П 2 ) ( П 1 , П 2 )

Как видно, алгоритм адаптивного спектрального рассогласования также даёт результаты существенно лучше RXD-алгоритма, при этом (в отличие от алго- ритма пространственно-спектрального рассогласования) он не предполагает использования никакой модели изображения. К его недостаткам по сравнению с алгоритмом пространственно-спектрального рассогласования можно отнести: неустойчивость (в общем случае) оператора проектирования, необходимость его регуляризации и большие вычислительные затраты. Это накладывает определённые сложности на практическое применение этого алгоритма.

Рис. 6. Результат работы адаптивного метода обнаружения аномалий

На рис. 8 приведён пример применения алгоритмов спектрального согласования и модификаций RXD-алгоритмов к реальному гиперспектральному изображению Moffett Field гиперспектрометра AVIRIS, представленному на рис. 7.

Для алгоритмов спектрального рассогласования размеры внутреннего окна составляли 3×3 отсчёта, размеры внешнего окна – 5×5 отсчётов . Локальный алгоритм RXD использовался с окном размером 5×5. Из очевидных недостатков алгоритмов RXD следует отметить их значительно меньшую помехоустойчивость, особенно локальной версии алгоритма. Результаты алгоритма пространственно-спектрального рассогласования выглядят визуально предпочтительнее, однако здесь следует отметить значительную сложность в интерпретации и оценке полученного результата.

Экспериментальное исследование алгоритма вероятностного обнаружения аномалий

При использовании алгоритма вероятностного обнаружения аномалий для обработки гиперспектральных изображений предпочтительно использовать в качестве входных данных изображения, полученные в результате одного из преобразований понижения размерности. Например, могжет быть использован метод главных компонент или метод независимых компонент [20], часто применяемые для работы с гиперспектральными изображениями. Понижение размерности часто необходимо, поскольку в противном случае число возможных значений квантованного вектора оказывается слишком велико и практически все значения отсчётов оказываются уникальными. Число компонент представления оказывается в этом алгоритме дополнительным независимым параметром, который также следует подбирать для каждой конкретной задачи .

Для исследования алгоритма вероятностного обнаружения аномалий использовались:

ченных изображений результаты предложенного алгоритма выглядят предпочтительнее.

Рис. 7. Изображения Moffett Field гиперспектрометра

AVIRIS: а) канал 20, 550,3 нм; б) канал 80, 1110,594 нм;

• в ) канал 160, 1873,184 нм; г) канал 220, 2457,3479 нм

• -    изображения коэффициентов, полученные методом главных компонент [20], для обработки гиперспектральных изображений,

• -    мультиспектральные изображения, изначально содержащие небольшое число спектральных компонент.

На рис. 9 и 10 приведены соответственно тестовый фрагмент трёхканального снимка UK DMC и результат работы алгоритма при K = 4. Количество уровней квантования выбиралось небольшим, рекомендуемые значения – три или четыре уровня. Для сравнения на рис. 11 и рис. 12 приведены результаты работы RXD-алгоритма (глобального и локального соответственно). На основе визуальной оценки полу-

б)

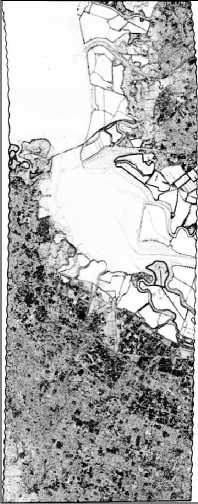
Рис.8. Результаты применения алгоритмов обнаружения аномалий к изображению Moffett Field гиперспектрометра AVIRIS: а) алгоритм пространственно-спектрального рассогласования; б) адаптивный алгоритм спектрального рассогласования; в) RXD-алгоритм (глобальный);

г) RXD-алгоритм (локальный, окно 5×5)

Другой пример обработки реального – гиперспектрального – изображения представлен на рис. 13.

На рис. 14 представлен пример с синтезированным гиперспектральным изображением, демонстри-

рующий очевидное преимущество предложенного алгоритма. На синтезированном изображении размером 512×512 с 340 каналами были синтезированы две области, сигнатуры областей значительно отли-

чались друг от друга.

ственно-спектральный и адаптивный спектральный с модификацией) и алгоритм вероятностного обнаружения аномалий.

Рис.10. Результат работы алгоритма вероятностного

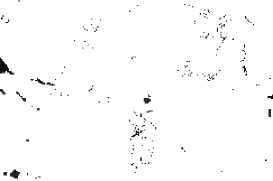
обнаружения аномалий при K = 4 . а) поле значений

«аномальности», б) аномальны е зоны для квантиля в 2 %

Рис.11. Результат работы глобального RXD-алгоритма: а) поле значений «аномальности», б) аномальные зоны для квантиля в 2 %

б)

б)

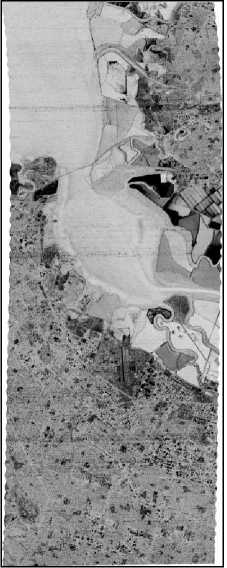
а)

б)

Рис.12. Результат работы локального RXD-алгоритма:

• а)    поле значений «аномальности»,

• б)    аномальные зоны для квантиля в 2 %

К областям в каждом канале добавляется аддитивный шум с нулевым средним и отношением сигнал/шум 1000. Для задания «аномалии» выбиралась новая сигнатура, которая была «близка» (в спектральном пространстве) к полусумме сигнатур исходных областей. Эта сигнатура использовалась для задания отсчётов «границы» между областями, формируя область «аномальности» для данного изображения. Результаты обнаружения такой области различными алгоритмами приведены на рис. 14 б-г : б о льшим значениям «аномальности» соответствуют более тёмные отсчёты изображения-результата.

Из этих результатов очевидна абсолютно корректная (ожидаемая) работа алгоритма вероятностного обнаружения аномалий, полностью некорректная работа глобального RXD-алгоритма (в качестве аномалии указана область изображения, расположенная в верхней правой части изображения и занимающая практически половину изображения) и близкая к неудовлетворительной работа локального RXD-алгоритма.

Выводы

В статье предложен ряд новых алгоритмов обнаружения аномалий на гиперспектральных изображениях: алгоритмы спектрального рассогласования (простран-

Рис.14. а) Входное изображение, б) RXD-алгоритм (глобальный), в) RXD-алгоритм (локальный), г) алгоритм вероятностного обнаружения аномалий с числом уровней квантования K=4

Алгоритмы используют различные способы определения факта «аномальности», базируясь на различных математических моделях изображения и/или используя различные аспекты понятия «аномальности». Выполняется сравнение предложенных алгоритмов с широко используемыми вариантами RXD-алгоритма (глобальным и локальным), показано убедительное превосходство предложенных решений по сравнению с указанными существующими.

Рис.13. Результаты применения алгоритмов обнаружения аномалий к изображению Moffett Field гиперспектрометра AVIRIS: а) алгоритм вероятностного обнаружения аномалий; б) RXD-алгоритм (глобальный)

Проведён сравнительный анализ достоинств и недостатков предложенных алгоритмов. В частности, показано, что алгоритм пространственно-спектрального рассогласования устойчив к шуму и позволяет уверенно обнаружить аномалии на изображениях, удовлетворяющих модели стационарного случайного поля, даже при сильных искажениях. Алгоритм адаптивного спектрального рассогласования такой модели не использует, но является более вычислительно затратным и требует подбора параметра регуляризации. Оба алгоритма спектрального рассогласования на рассмотренных примерах оказались эффективнее, чем известный RXD-алгоритм.

Алгоритм вероятностного обнаружения аномалий использует принципиально новый метод поиска аномалий, заключающийся в «снижении» избыточности гиперспектрального представления отсчёта путём пере-квантования его спектральных коэффициентов. Указанная операция, которая может применяться и к исходному представлению гиперспектрального изображения, и к его представлению с сокращённой размерностью (например, с использованием главных компонент), позволяет дальнейший поиск «аномальных» отсчётов свести к простейшему анализу одномерной гистограммы, построенной для значений хэш-функции квантованного гиперспектрального отсчёта анализируемого изображения. Данный факт позволяет говорить о принципиально новом решении, не попадающем в принятую классификацию большинства существующих алгоритмов обнаружения аномалий. Сравнение результатов работы этого алгоритма с известными также показало его эффективность и значительное преимущество на одной из типовых для гиперспектральных изображений задач.

Работа выполнена при частичной финансовой поддержке:

• -    грантов РФФИ, проекты № 13-07-12103-офи-м, 13-01-12080-офи-м, 12-07-00021-а, и 13-07-97006-р_по-волжье_а;

• -    программы фундаментальных исследований Президиума РАН «Фундаментальные проблемы информатики и информационных технологий», проект 2.12;

• -    Министерства образования и науки Российской Федерации (в рамках постановления Правительства Российской Федерации от 09.04.2010 г. № 218: договор № 02.Г36.31.0001 от 12.02.2013).