Обнаружение аномалий трафика сети с помощью методов понижения размерности

Аномалии трафика компьютерных сетей являются проявлениями возможных сбоев в работе сетевого оборудования, программного обеспечения, а также могут быть следствием различного рода сетевых атак. В связи с этим обнаружение аномалий сетевого трафика имеет важное прикладное значение, так как позволяет оперативно реагировать на возможные аварийные ситуации и предотвращать различную злонамеренную сетевую активность. Актуальность обнаружения аномалий сетевого трафика растет синхронного с глобальным ростом сети Интернет, числа подключенных к компьютерным сетям пользовательских устройств и устройств Интернета вещей [1; 2; 5; 8; 9].

Определение аномалий (anomaly detection) представляет собой область анализа данных, посвященную определению тех значений в наборе данных, которые выходят за некоторый диапазон ожидаемых величин. Для таких значений также применяют термины исключения или выбросы. Обычно выделяют три основных вида аномалий [1; 2]:

– точечная аномалия (выброс): экземпляр данных, значительно отклоняющейся от средних значений рассматриваемого набора данных;

– коллективная аномалия: группа из близко расположенных выбросов, вероятно вызванных одним и тем же событием;

– контекстная аномалия: экземпляр данных, являющийся выбросом только при соблюдении определенных условий.

Ключевым аспектом проблемы обнаружения аномалий является характер исходных данных, которые чаще всего представляют набор отдельных экземпляров: наблюдений, записей, объектов, точек, векторов и т.п. Экземпляры могут описываться одним (одновариантные данные) или несколькими (многовариантные данные) атрибутами. Атрибуты также могут быть одного или разных видов: бинарные, категориальные, непрерывные и т.д. [1].

В случае трафика компьютерных сетей экземплярами данных обычно являются пакеты, передаваемые по сети, которые могут быть описаны множеством таких атрибутов как: IP-адрес источника, IP-адрес назначения, длина пакета в байтах, время поступления, тип транспортного протокола, номер порта источника, номер порта назначения и др [6].

Исходные данные также можно охарактеризовать отношениями между отдельными экземплярами. Наиболее часто, при выявлении аномалий экземпляры данных считаются независимыми друг от друга. Однако в общем случае такая зависимость имеет место. Это может быть, например, зависимость от времени: скорость обработки пакетов сетевым устройством зависит от скорости поступления предыдущих пакетов. Также могут иметься зависимости от характера пакетов, например, ряд сетевых протоколов для передачи данных требуют установки и поддержания соединения с использованием пакетов определенных типов. Учет таких зависимостей может значительно усложнить обнаружений аномалий [1].

Можно выделить следующие основные виды методов, применяемых для обнаружения аномалий сетевого трафика [5; 8; 9]:

– методы на основе сигнатур;

– статистические методы;

– методы машинного обучения.

Методы на основе сигнатур (signature-based), также называемые методами на основе правил (rule-based) часто применяют в системах обнаружения вторжений (IDS – Intrusion Detection Systems). Сигнатура представляет собой правило, при помощи которого IDS производит проверку пакетов, передаваемых по сети. В случае, если пакет попадает под запрещающее правило, IDS сигнализирует о подозрительной аномальной сетевой активности. Список сигнатур должен быть заранее подготовлен и загружен в IDS. Преимуществом методов на основе сигнатур является простота реализации, главный недостаток – необходимость предварительной подготовки и постоянного обновления большого списка сигнатур для быстрого реагирования на все возможные и новые виды сетевых атак [5; 8].

В основе статистических методов лежит предположение о том, что аномалии являются редким событием и расположены в областях с низкой ве- роятностью. В статистических методах на основе наблюдаемых данных производится определение стохастической модели, после чего новые экземпляры данных тестируются на принадлежность к этой модели. Экземпляры с низкой вероятностью считаются аномалиями [1; 17]. Статистические методы подразделяют на две группы: параметрические и непараметрические. В параметрических методах заранее подбирается закон распределения данных, параметры которого определяются на основе тренировочных данных. Примерами параметрическим методов являются гауссовские и регрессионные методы, такие как метод скользящего среднего и ARIMA. В непараметрических методах стохастическая модель полностью определяется на основе тренировочных данных. К непараметрическим методам относят методы гистограмм и функций ядра. Преимуществами статистических методов является возможность работы с неразмеченными данными и отсутствие необходимости в предварительной подготовки и загрузке правил. Основной недостаток: точность выявления аномалий напрямую зависит от верного определения и подгонки стохастической модели, что часто затруднено на практике [1].

Методы машинного обучения традиционно подразделяют на два основных типа: обучения с учителем (supervised learning) и без учителя (unsupervised learning). Методы обучения с учителем обучаются на заранее размеченных данных. Определение аномалий в этом случае сводится к задаче бинарной классификации данных на нормальные и аномальные. К методам такого типа относят большинство методов машинного обучения: k-ближайших соседей (kNN), деревьев принятия решений (Decision Trees), опорных векторов (SVM), искусственных нейросетей (ANN). Преимуществами использования методов обучения с учителем для обнаружения аномалий является простота реализации, высокая точность и устойчивость к различным негативным факторам. Главный недостаток заключается в том, что эффективность методов напрямую зависит от доступности размеченных тренировочных данных [1, 2]. Трафик компьютерных сетей может состоять из миллионов пакетов в секунду, что крайне затрудняет ручную разметку данных [5; 6].

В методах обучения без учителя алгоритмы обучаются на неразмеченных данных, структурируя их каким-либо образом, что делает данные методы предпочтительными для выявления аномального трафика. К методам обучения без учителя относят такие группы методов как кластеризации и понижения размерности. В методах кластеризации, напри- мер k-средних, предполагается, что обычные данные располагаются близко в пространстве и формируют плотные кластеры, в то время как аномалии либо не принадлежат к какому-либо кластеру, либо формируют разреженные кластеры. Основным преимуществом алгоритмов кластеризации является возможность обнаружения как точечных, так и групповых аномалий. Недостатками являются высокая вычислительная сложность, в зависимости от реализации, и то, что большая часть таких алгоритмов не адаптирована для обнаружения аномалий и принудительно группирует все данные в кластеры [1].

Методы понижения размерности (dimensionality reduction) производят преобразование данных из пространства с высокой размерностью в пространство низкой размерности, при этом удерживая основные их свойства. Такие методы могут применяться для обнаружения редких аномалий за счет того, что такие аномалии практически не оказывают влияние на само преобразование и ошибка реконструкции аномальных данных значительно выше нормальных. Преимуществами алгоритмов данного типа является хорошая адаптируемость для выявления точечных аномалий, относительно низкая вычислительная сложность. Основной недостаток заключается в том, что предположение о редкости аномалий не всегда выполняется на практике [2; 4; 6] .

В подавляющем большинстве научных работ, посвященных обнаружению аномалий сетевого трафика, основное внимание уделяется одному выбранному методу и часто не приводится сопоставление результатов с широким кругом методов машинного обучения. Оригинальность данной научной работы заключается в рассмотрении и сопоставлении результатов большого количества методов обнаружения аномалий, основанных на понижении размерности данных.

Методы понижения размерности

На практике наиболее широко используются следующие методы понижения размерности [4; 7; 10-13]:

– метод главных компонент;

– сингулярное матричное разложение;

– неотрицательное матричное разложение;

– методы случайных проекций;

– методы на основе искусственных нейросетей.

Метод главный компонент является наиболее популярным методом понижения размерности и основан на ортогональной линейной трансформации данных в пространство меньшей размерности. Трансформация подбирается таким образом, чтобы компонент с наибольшей дисперсией скалярно проецировался на первую координату, второй компонент по величине дисперсии проецировался – на вторую и т.д. Компоненты с наименьшим значением дисперсии могут быть отброшены, так как их влияние на суммарную дисперсию данных незначительно.

Математически метод главных компонент можно выразить в матричном виде [10]:

P = W T - A , (1) где A - матрица исходных данных, m x n ; W -матрица преобразования главных компонент, n x n ; P - проекция данных, m x n .

В полученной проекции P k столбцов содержит нулевые или пренебрежимо малые значения, которыми можно пренебречь. В результате получаем итоговую проекцию P ', размерностью m x ( n - k ) .

Для нахождения матрицы преобразования W может использоваться несколько методов: на основе матрицы ковариации данных, сингулярного разложения, с использованием функций ядра и т.д.

Одним из популярных методов получения матрицы преобразования является сингулярное разложение матриц, которое также может быть использовано для снижения размерности. Сингулярное разложение выражается следующим матричным соотношением [11]:

A = U -S- V T . (2) где: Σ – диагональная матрица сингулярных величин матрицы A, m x n ; U и V - квадратные матрицы разложения размерностями m x m и n x n , соответственно. Для проекции данных в пространство пониженной размерности используются соотношения:

P = U -S = V - A . (3)

В неотрицательном матричном разложении исходная матрица A с неотрицательными элементами представляется в виде произведения матриц W, m x p и H, p x n также не содержащих отрицательных элементов [12]:

A = W - H . (4)

На практике значение p может быть значительно меньше как m, так и n, что позволяет эффективно применять данный метод для понижения размерности. В качестве проекции обычно используется матрица W. Существуют несколько алгоритмов реализации данного метода: мультипликативного обновления весов, градиентного спуска, неотрицательных наименьших квадратов и др. Основным ограничением метода является требование к неотрицательности элементов всех матриц.

Методы случайных проекций основаны на лемме о малом искажении, также известной как лемма Джонсона–Линденштрауса: множество n– точек многомерного пространства можно отобразить в пространство значительно меньшей размерности почти без изменения расстояния между точками. Математически такое преобразование описывается выражением [13]:

P = R - A . (5) где A - матрица исходных данных, m x m ;

R - матрица случайного преобразования, k x m ;

P - проекция данных, k x n .

Случайная матрица R может быть сгенерирована, используя гауссовское распределение, которое удовлетворяет следующим требованиям: сферической симметрии, строки в R должны быть ортогональными и являться векторами единичной длины. Основным преимуществом методов случайных проекций является низкая вычислительная сложность. Недостаток заключается в слабом использовании статистических свойств данных.

Методы машинного обучения, основанные на искусственных нейронных сетях, также могут применяться для понижения размерности данных. Основным типом нейросетей применяемым для этих целей является автокодировщик (autoencoder) [1–3]. В простейшем варианте автокодировщик представляет собой многослойный персептрон, у которого число нейронов в скрытом слое (h) меньше числа нейронов во входном слое ( x ) и выходном слое ( y ), рисунок 1. При обучении автокодировщика происходит сравнение исходных данных, подаваемых на входы нейросети, с их реконструкцией на выходах. Полученная таким образом ошибка реконструкции при помощи алгоритма обратного распространения корректирует значения связей нейронов скрытого слоя. В результате, нейроны скрытого слоя обучаются сжатой репрезентации исходных данных. Преимуществом автокодировщика является простота реализации, главный недостаток – как и других нейросетевых методов – высокие требования к объему тренировочных данных, памяти и вычислительных ресурсов для обучения.

Методы кластеризации также могут применяться для понижения размерности данных, однако для большинства методов обратная реконструкция невозможна, что не позволяет их использовать для обнаружения аномалий. К исключениям относится агломеративная кластеризация по свойствам (feature agglomeration), в которой вначале пары близких параметров объединяются в кластеры, пары ближайших кластеров объединяются в более крупные кластеры и т.д. Таким образом, получают иерархическое дерево кластеров – дендограмму. В качестве меры близости может использоваться расстояние в евклидовом пространстве. При достижении необходимого количества кластеров производится «обрезание» дендрограммы [6, 14].

показывает отношение правильно выявленных случаев аномальности – TP к общему числу аномалий в данных как выявленных – TP, так и не

выявленных – FN ( False Negative):

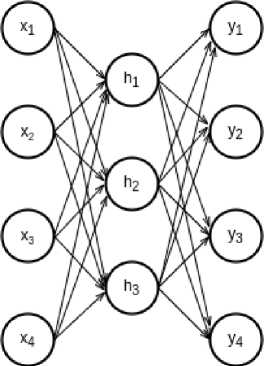
Рисунок 1. Схема простого автокодировщика

Recall =

TP

TP + FN

Оценка методов обнаружения аномалий

В общем случае при использовании методов понижения размерности для оценки степени аномальности экземпляра данных используется среднеквадратическая ошибка реконструкции [6, 7]:

Чувствительность имеет обратную зависимость от величины порогового значения ф , чем ниже порог, тем большее число аномалий будет выявлено, включая и неправильно определяемые экземпляры как аномальные. Таким образом пороговое значение ф должно быть подобрано так, чтобы обеспечивался баланс между точностью и восприимчивостью. Для выбора оптимального порогового значения можно использовать зависимость между точностью и восприимчивостью (precision–recall curve), в которой по оси абсцисс откладывается восприимчивость, а по оси ординат – точность.

На практике для сопоставления различных методов машинного обучения используется усредненная оценка точности (average precision score) вычисляемая по формуле [7]:

AP = 2 , ( Recall, - Recall, - 1 ) Precision, ,    ⁽⁹⁾

RMSE = ¹ X П_/У, - y /) 2 , n

где Precision и Recall – точность и восприимчивость для порогового значения ф , .

Чем выше значение усредненной оценки точ-

где n – размерность данных; y – исходное значение; y ‘' - реконструированное значение.

Полученное значение RMSE сравнивается с пороговой величиной ф : если RMSE > ф , то рассматриваемый экземпляр данных считается аномалией.

В качестве общей оценки способности метода по обнаружению аномалий применяется такой параметр как точность или меткость (precision). Точность показывает отношение числа правильно отнесенных экземпляров к аномалиям – TP ( True Positive), к общему числу экземпляров, отнесенных к аномалиям как правильно – TP , так и неправильно – FP ( False Positive) [6, 7]:

ности, тем лучше решение.

Другой часто применяемой оценкой качества бинарной классификации метода является кривая рабочей характеристики приемника (ROC – Receiver Operating Curve). ROC – это зависимость чувствительности или доли правильно классифицированных экземпляров как аномальные – TPR (True Positive Rate) от доли ошибочно классифицированных экземпляров как аномалии – FPR (False Positive Rate) при различных значениях ф , [7]. В общем случае значение TPR совпадает со значением Recall , параметр FRP определяется по формуле:

FPR =

FP

FP + TN

Precision =

TP

TP + FP

Очевидно, что точность напрямую зависит от выбранного порога ф , чем выше его значение, тем выше точность. Однако с повышением порогового значения также падает и общее число выявляемых аномалий в данных. Для оценки способности метода по выявлению аномалий используется такой параметр как восприимчивость или чувствительность (recall). Чувствительность

где FP – неправильно классифицированные экземпляры как аномалии, TN (True Negative) – правильно классифицированные экземпляры как не являющиеся аномалиями.

Пример ROC характеристики представлен на рисунке 2.

Чем более вытянутый вид к оси TPR имеет ROC–характеристика, тем лучше метод выполняет классификацию. Идеальный бинарный классификатор имеет значения TPR = - и FRP = 0 .

Для сопоставления различных методов удобно использовать площадь области под ROC характеристикой, которая обозначают как AUC (Area Under Curve). Для идеального классификатора AUC = 1 .

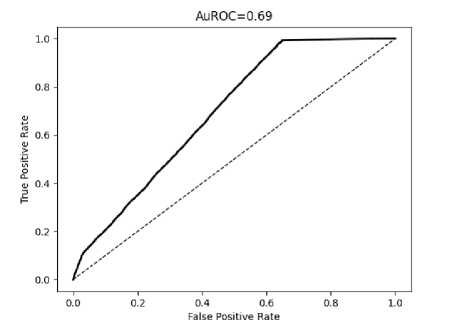
Рисунок 2. Пример ROC характеристики

Описание исходных данных

Исходные данные, использованные в работе, представляют собой набор параметров трафика, собранного учеными университета имени Бен– Гуриона, на участке сети видеонаблюдения при воздействие различного рода сетевых атак [15]. Каждый экземпляр данных в наборе представляет собой параметры отдельного пакета, сгенерированные при получении. Пакет описывается вектором из 23 параметров, таких как [6]:

– данные МАС–адрес и IP–адрес источника (SrcMAC–IP);

– IP–адрес источника (SrcIP);

– данные IP–адреса источника и назначения (Channel);

– данные номера портов TCP/UDP источника и назначения (Socket) и др.

Кроме того, также учитываются значения собранных параметров и за предыдущие интервалы времени в 100 мс, 500 мс, 1,5 с, 10 с и 1 мин. В итоге получается вектор, состоящий из 115 значений.

Аномальный трафик представлен следующими видами сетевых атак:

– сканирование портов хостов в сети (OS Scan);

– фаззинг – посылка случайных команд на веб-интерфейсы видеокамер (Fuzzing);

– перехват трафика через подделку ARP (ARP MitM);

– заражение устройств в сети червем Mirai (Mirai);

– SYN DoS атака на веб–сервер видеокамер (SYN DoS);

– активный перехват трафика путем установки моста на кабель (Active Wiretap);

– вставка видеоклипа в видеопоток (Video Injection);

– переполнение сети сообщениями протокола SSDP (SSDP Flood);

– блокирование видеопотока путем посылки пакетов переключения режимов SSL к камерам (SSL Renegotiation).

Общий объем параметров трафика занимает примерно 60 Гб. Вначале набора данные представлены только нормальным трафиком, затем начинается аномальная активность.

Результаты моделирования

Для моделирования весь объем данных был разделен на две части: для проведения обучения (70%) и тестирования (30%) методов.

При моделировании использовались следующие методы понижения размерности:

– метод главных компонент (PCA);

– сингулярное разложение (SVD);

– неотрицательное матричное разложение (NMF);

– гауссовских случайных проекций (GRP);

– автокодировщик (AEN).

Кроме методов понижения размерности данных для сопоставления также применялись методы:

– обучения с учителем на основе многослойного персептрона (MLP);

– агломеративная кластеризация по свойствам (FA).

Для моделирования применялись реализации методов понижения размерности и параметры оценки из пакета Scikit–Learn. Для реализации методов с использованием нейронный сетей применялся пакет TensorFlow. Исходные коды всех использованных моделей в формате Jupyter Notebook представлены в репозитории [16].

Примеры, полученных в результате моделирования, значений AP и AUC в виде столбчатых диаграмм представлены на рисунках 3–10.

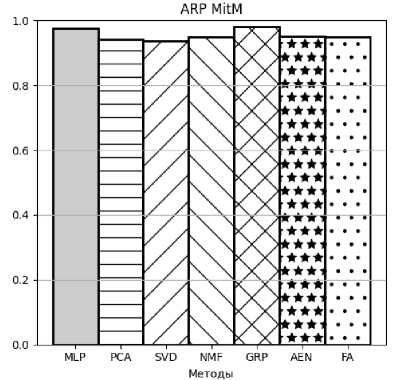
Рисунок 3. AP для ARP MitM атаки

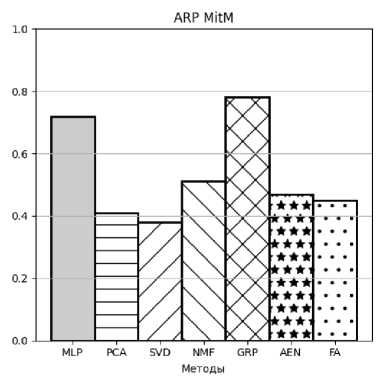
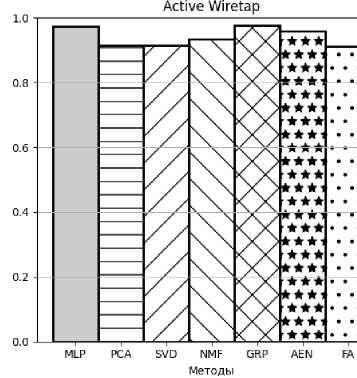
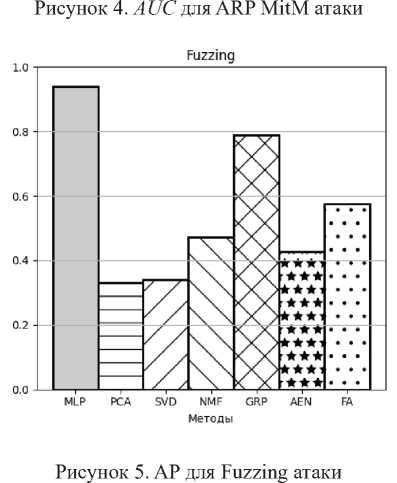
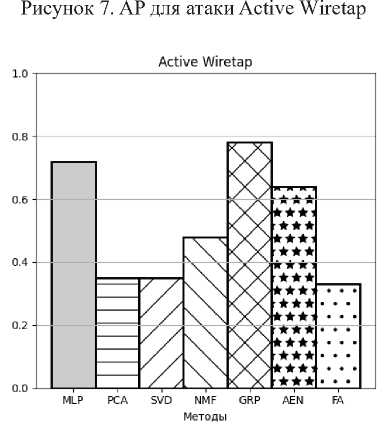
Рисунок 8. AUC для атаки Active Wiretap

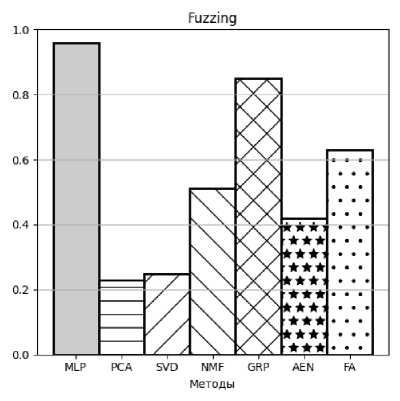
Рисунок 6. AUC для Fuzzing атаки

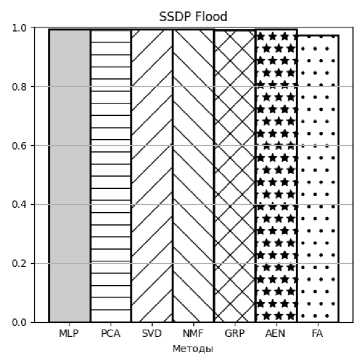
Рисунок 9. AP для атаки SSDP Flood

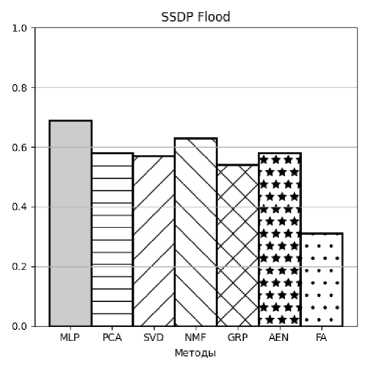
Рисунок 10. AUC для атаки SSDP Flood

Заключение

В статье рассмотрено приложение различных методов понижения размерности данных для обнаружения аномалий в трафике компьютерной сети. Выполнено их сопоставление с другими методами. Полученные результаты моделирования показывают, что для большей части атак хорошие показатели обнаружения аномалий обеспечивает метод гауссовских случайных проекций. Данный метод также имеет самые низкие требования к вычислительным ресурсам. С учетом того, что на большинстве сетевых устройств, например маршрутизаторов, вычислительные ресурсы, как правило, весьма ограничены, можно рекомендовать метод гауссовских проекций для использования на сетевых устройствах для выявления аномалий трафика.