Обнаружение оптических сигналов при приёме потока фотоэлектронов с неизвестной формой плотности

Задача приёма слабых оптических сигналов на фоне шумов представляет значительный интерес при разработке и исследовании систем связи, оптической локации (в координаторах цели лазерных головок самонаведения, авиационных, артиллерийских и танковых лазерных прицелах, биноклях-дальномерах) [1, 2 и др.]. Оптический сигнал в виде светового поля распространяется в канале связи, далее на приёмной стороне оптическое поле собирается оптикой приёмника и детектируется фотодетектором. Основным способом приёма оптического сигнала является так называемое прямое детектирование (энергетический приём), при котором оптический сигнал направляется на фотодетектор и на его выходе образуется электрический сигнал (фототок). В отличие от приёма сигналов в радиосвязи и радиолокации, когда шумы и помехи практически всегда можно считать независимыми, детектирование оптических сигналов сопровождается неустранимым дробовым шумом, статистические характеристики которого тесно связаны со значением самого сигнала. Причём дисперсия дробового шума в каждой точке оси времени пропорциональна интенсивности сигнала в той же точке. При этом выходной сигнал фотоприёмника можно представить в виде аддитивной комбинации двух составляющих, одна из которых пропорциональна оптическому сигналу, а другая – случайная – является дробовым шумом, рождённым самим этим сигналом. Однако эту информацию можно учесть и использовать при синтезе обнаружителей оптических сигналов на фоне комплекса шумов (дробовых, тепловых и др.) только в случае, если имеются априорные сведения о параметрах и форме сигналов. В противном случае приходится полагать, что форма оптического сигнала (точнее, его плотность потока как функция времени) априори неизвестна.

Как показано в [1], форма оптических импульсов может оказывать существенное влияние как на эффективность их обнаружения, так и на точность оценки неизвестных параметров, например, временного положения. Однако в большинстве известных работ (см., например, [3, 4]) подобная задача решалась в предположении о том, что форма плотности потока сигнала и шума является известной. Итак, предположим, что наблюдению на интервале времени [0, T] доступна некоторая реализация, представляющая собой либо аддитивную смесь оптического сигнала с неизвестной формой интенсивности и фоновым излучением (гипотеза Н1), либо только фоновое излучение (гипотеза Н0). Далее в соответствии с теорией фотоэффекта [5] примем, что поток первичных фотоэлектронов и, соответственно, поток одноэлектронных импульсов на выходе фотоумножителя или лавинного диода подчиняется распределению Пуассона. Что касается статистики первичных электронов, то при приёме когерентного излучения эта модель адекватна реальности. Если же принимается тепловое излучение, то при условии, что длительность времени измерения превышает время когерентности, соответствующее этому случаю биноминальное распределение фотоотсчётов с отрицательным показателем также переходит в пуассоновское [6]. Однако следует отметить, что реальные фотодетекторы из-за сложности явлений размножения фотоэлектронов искажают исходные распределения фотоэлектронов [7]. Следовательно, подобную пуассоновскую модель следует рассматривать как первое приближение. Что касается фонового и теплового излучений, то, учитывая, что изменение во времени их интенсивности происходит существенно медленнее, чем изменение формы используемых сигналов, в дальнейшем будем считать, что значения плотности потока (интенсивности) фона и соответствующего ему дробового шума могут быть заранее оценены. С учётом этого в дальнейшем полагаем, что плотность потока фонового излучения известна и постоянна. Что касается темнового тока фотодетектора, то он также может быть учтён путём соответствующей коррекции значений фонового излучения [8].

Перейдём теперь к нахождению алгоритма обнаружения оптического сигнала с неизвестной формой интенсивности λ _s ( t ) при наличии фонового излучения с известной постоянной интенсивностью λ ₀ . В соответствии с принятой нами моделью поток фотоэлектронов подчиняется закону Пуассона. Это значит, что вероятность насчитать N i фотоэлектронов на интервале времени ∆ t вблизи точки t_i определяется как

ГХ ( t i ) А t "I ^{N i}

P ⁽ N i ’ t i ) =----- ы I ^J exP l- ^X ( t i ) ^A t I ,          ⁽¹⁾

N_i !

Подставляя эту оценку в (3), находим следующее выражение для логарифма отношения правдоподобия:

где Х ( t ) = Х s ( t ) + Х ₀ при выполнении гипотезы Н 1 либо Х (t ) = Х ₀ при выполнении гипотезы Н 0 .

Совместная вероятность выпадения N_i фотоэлектронов на интервалах длительности A t в точках t ₁ , t ₂ , ... t_M (функция правдоподобия) в силу независимости пуассоновских отсчётов будет определяться произведением вида

M

i =1

При выполнении гипотезы Н 1 из (1), (2) получим следующее выражение для логарифма функции правдоподобия:

M

lnp =£{- ln[Xs (ti ) + Xo]- i =1 '

- ln ^(A t ^)-[x s ⁽ t i ^{) + X} 0 | ^A t ^- ln ⁽ N i ^{! )} } .

M I

Л = У Ni i=1 I

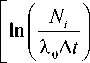
- 1

x u (— -Xo At),

+ XoAt ^x

Аналогично, при выполнении гипотезы Н 0 логарифм функции правдоподобия:

M lnP = £{- ln(Xo)-ln(At)-XoAt-ln(- !)}.

i =1

Из этих выражений находим логарифм отношения правдоподобия

Л = ln P 1 - ln P ₀ =

= f.

y

N_i ln

1 + ^Х 't '

X o

^-X s ⁽ t i ^)A t ’ .

Заметим, что это выражение получено в предположении, что интенсивность оптического сигнала Х s ( t ) известна.

Для нахождения решающей статистики в случае априори неизвестной формы интенсивности сигнала поступим следующим образом. В выражении (3) Х s ( t i ), ( i = 1,2,... M ) - неизвестные величины.

Определим оценки этих величин, исходя из следующей системы уравнений максимального правдоподобия:

дЛ

дХ s (t)

л

Х s ( t i )

= 0.

Из этой системы уравнений находим

N-

Х s ( t i ) =     -X o .

A t

Учитывая неотрицательность интенсивности, положим

ZX

Х s ( t i ) =

n , /А t -x _o, n , >X _o a t , o,           n , >X o A t .

где u ( x ) = 0 при x >  0 и u ( x ) = 1 при x <  0 .

Таким образом, алгоритм обнаружения оптического сигнала с неизвестной формой интенсивности при наличии фонового излучения должен заключаться в формировании величины Л (4) и сравнении её с некоторым порогом h , определяемым из заданного критерия эффективности. В дальнейшем в качестве критерия эффективности будем рассматривать критерий идеального наблюдателя [9], в соответствии с которым необходимо минимизировать полную (среднюю) вероятность ошибки P_e . Средняя вероятность ошибки P e определялась как ( а + Р ) / 2 , где а - вероятность превышения порога обнаружения решающей статистикой (4) при выполнении гипотезы H 0 (отсутствие полезного сигнала на входе приёмника). Вероятность Р - это вероятность непревышения порога обнаружения решающей статистикой (4) при выполнении гипотезы H 1 (наличие полезного сигнала на входе приёмника). Определение вероятности ошибки P_e осуществлялось с помощью статистического моделирования на ЭВМ по 50000 реализаций сигнала с фоном (гипотеза Н 1 ) и только фона (гипотеза Н 0 ) . При моделировании в случае выполнения гипотезы H 0 осуществлялось формирование пуассоновского потока с плотностью Х ₀, рассчитывалось количество фотоэлектронов на интервале наблюдения, формировалась достаточная статистика в соответствии с формулой (4) и осуществлялось сравнение с набором пороговых значений. При превышении порога фиксировалась ошибка. Вероятность а ( h ) определялась как отношение количества превышений порога h в N испытаниях к количеству этих испытаний. Аналогичным образом вычисляется вероятность Р ( h ), за исключением того, что при формировании пуассоновского потока его плотность предполагалась равной Х ₀ +Х _s ( t ). После получения вероятности P e ( h ) = ( а ( h ) + Р ( h )) / 2 для набора пороговых значений h определялся тот порог, при котором эта вероятность минимальна. Эта вероятность и представляет собой искомую среднюю вероятность ошибки.

Рассматривались две задачи: обнаружение сигнала с известным временем прихода (для определённости полагаемым равным нулю) и со случайным (равномерно распределённым на интервале наблюдения) временем прихода. При моделировании полагалось, что форма интенсивности сигнала имеет экспоненциальный вид, а именно:

Х s ( t ) = Ie -^ t - t ⁰ ) u ( t - 1 o ),

где t ₀ – момент прихода сигнала (равный либо 0, либо принимающий случайные значения от реализации к реализации на интервале наблюдения [0; Т – T 0 ]), где T 0 – длительность сигнала по уровню 0,9 от его полной энергии.

Были исследованы зависимости вероятности средней ошибки P e от параметров: v = у T , gn = Х ₀T и отношения сигнал/шум:

T q = 1

^ * ( t ) ^ T

U d t ≃

v gn

где U = IT .

Здесь параметр v характеризует скорость изменения плотности потока во времени; чем больше параметр v , тем быстрее изменяется плотность потока. Параметр gn – это интегральная плотность потока фонового излучения.

На рис. 1 приведены зависимости P_e ( M ) при априори известном времени прихода t ₀ = 0 , а на рис. 2 – при случайном времени прихода оптического сигнала. Кривые 1 на этих рисунках построены при v = 10, gn = 20, q = 1, кривые 2 - при v = 10, gn = 20, q = 0,5, кривые 3 - при v = 5, gn = 20, q = 1, кривые 4 - при v = 5, gn = 20, q = 0,5 и, наконец, кривые 5 - при v = 10, gn = 10 , q = 1.

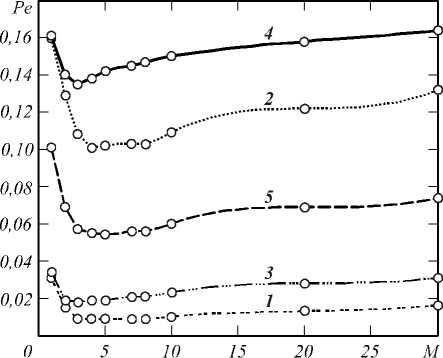
Рис. 1. Зависимость вероятности полной ошибки от числа интервалов разбиения M (t₀ = 0)

Из анализа рис. 1 и 2 можно сделать следующие выводы. Естественно, средняя вероятность обнаружения при случайном времени прихода больше по сравнению со случаем априори известного и постоянного времени прихода. Кроме того, в обоих случаях (в первом – более явно, во втором – менее) в зависимостях Pe (M) наблюдаются минимумы. Следовательно, в алгоритме (4) величина M не должна выбираться слишком большой, как следует из стандартных умозаключений. Малые значения параметра M -1 + 3 приводят к завышенным в несколько раз вероятностям ошибки, что достаточно очевидно, так как при этом интервалы разбиения являются слишком большими и в результате на оценку интенсивности сигнала будет оказывать существенное влияние фоновое излучение. Если же M велико, то увеличивается количество оцениваемых параметров, что также приводит к росту вероятности ошибки. Видно, что для рассматриваемых случаев оптимальное значение M , обеспечивающее минимум средней вероятности ошибки, должно быть порядка 4÷7.

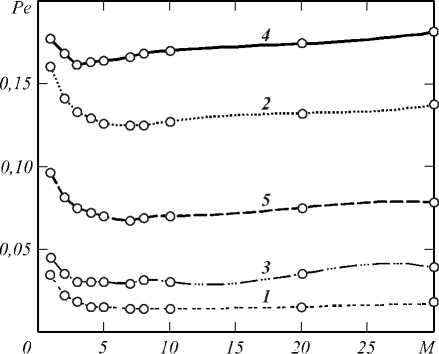
Рис. 2. Зависимость вероятности полной ошибки от числа интервалов разбиения M ( t0 – случайно)

На рис. 3 и 4 изображены зависимости P_e ( q ) также при 1 ₀ = 0 и при случайном времени прихода соответственно.

На рис. 5 и 6 приведены зависимости P_e ( gn ) при аналогичных условиях наблюдения.

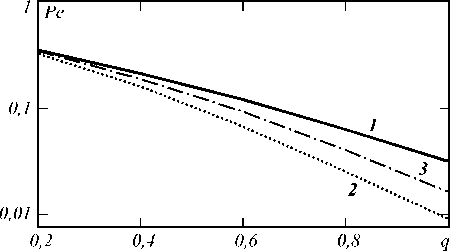
Рис. 3. Зависимость вероятности полной ошибки от отношения сигнал/шум q (t₀ = 0)

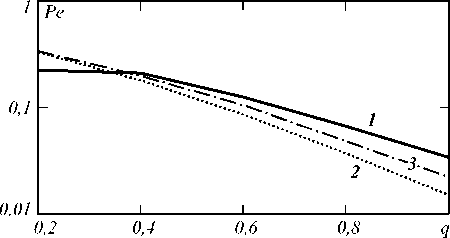
Рис. 4. Зависимость вероятности полной ошибки от отношения сигнал/шум q (t0 – случайно)

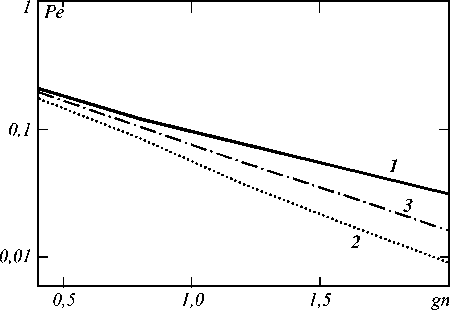
Рис. 5. Зависимость вероятности полной ошибки от интегральной интенсивности фона gn (t₀ = 0)

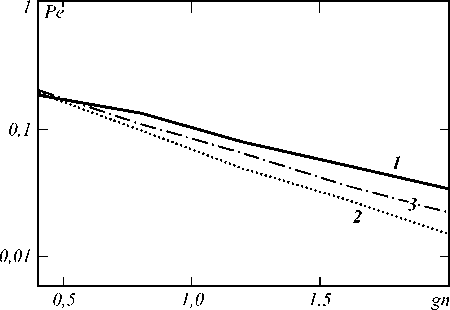
Рис. 6. Зависимость вероятности полной ошибки от интегральной интенсивности фона gn (t0 – случайно)

Рис. 3 и 4 построены при g n = 2, а рис. 5 и 6 -при q = 1. На всех этих рисунках кривые 1 построены при M = 1, кривые 2 - при M = 4 и кривые 3 -при M = 30 . Как и ранее, подтверждается наличие оптимального значения параметра M ∼ 4 , обеспечивающего минимум средней вероятности ошибки. Кроме того, следует отметить следующий факт. При случайном времени прихода наименьшую среднюю вероятность ошибки обеспечивает выбор M = 1, если мало отношение сигнал/шум или мала интенсивность шума Х ₀. Однако подобные ситуации практического интереса не представляют, так как при этом средняя вероятность ошибки принимает слишком большие значения (больше, чем 0,1).

Отметим также, что, как и всегда [10, 11] в оптических задачах, средняя вероятность ошибки зависит не только от отношения сигнал/шум, но и от интенсивности фонового излучения (при постоянном отношении сигнал/шум).

Таким образом, с помощью компьютерного моделирования получены зависимости средней вероятности ошибки от различных параметров оптических сигнала и шума в случае неизвестной формы плотности потока сигнала. Следует отметить, что в известных работах по данной тематике синтез оптимальных структур обнаружителей при неизвестной форме плотности потока сигнала не был выполнен.

Влияние формы плотности потока сигнала в основном исследовалось либо на качественном уровне [8], либо определялся проигрыш по каким-либо характеристикам (например, ОСШ) при отклонении формы потока от предполагаемой [1]. В данной работе выполнены синтез и анализ оптимального алгоритма обнаружения оптического сигнала при отсутствии информации о форме плотности потока этого сигнала. Анализ приведённых результатов моделирования свидетельствует о следующем. Повышение эффективности обнаружения (наличие минимума в зависимости P e ( M ) при определённом значении параметра M ) не сильно зависит от отношения сиг-нал/шум. Подобная зависимость более явно проявляется при больших интенсивностях шума Х ₀ и при достаточно быстром изменении интенсивности сигнала во времени, т.е. при достаточно больших величинах параметра v = у T .