Обнаружение сдвига ветра на основе анализа карт ширины спектра сигнала, принимаемого метеорологическим радиолокатором

Для1 авиации большой интерес2 представляет информация о наличии такого опасного явления, как сдвиг ветра в пограничном слое атмосферы высотой до 500 м [1]. Современные метеорологические радиолокаторы предоставляют информацию о наличии данных явлений, но не с требуемым разрешением и не в указанном диапазоне высот [2]. В связи с этим большой интерес представляет исследование информации, которая может быть извлечена из поставляемых ими карт ширины спектра сигнала (рис. 1).

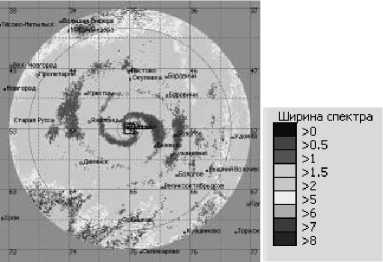
Рис. 1. Карта распределения ширины спектра по поверхности конического разреза

Авторами была выдвинута гипотеза о тесной связи вертикального профиля ветра с особенностями пространственного распределения параметра на указанных картах [3]. Для ее подтверждения была разработана аналитическая модель, с помощью которой получены карты для трех видов изменения ветра с высотой:

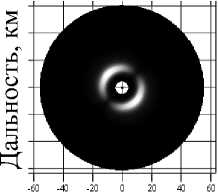
• 1)    два слоя гидрометеоров с различными векторами скорости в каждом из них (рис. 2а);

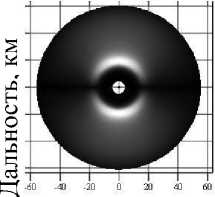
• 2)    два слоя, в одном из которых скорость

ветра равномерно изменяется по величине (рис. 2б);

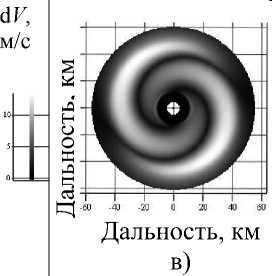
• 3)    два слоя с равномерным изменением

скорости и направления ветра в одном из них (рис. 2в).

Достаточно сравнить рис. 1 и 2в, чтобы убе- диться в том, что гипотеза хорошо согласуется с реальными результатами.

d V , м/с

Дальность, км

а)

Дальность, км б)

d V , м/с

Рис. 2. Карты распределения ширины спектра по поверхности конического разреза

Следующий шаг – решение обратной задачи восстановления профиля ветра на основе анализа полученной карты. Для этого была разработана математическая модель пространственного распределения ширины спектра радиальных скоростей гидрометеоров, на основании которой возможно не только обнаружить сдвиг ветра, но и оценить его количественные характеристики.

В поставленной задаче было принято, что метеоцель состоит из двух смежных слоев с разными отражаемостью, направлением и скоростью ветра в каждом из них. Параметры слоев следующие:

• –    первый слой: диапазон высот – от 0 до h ₁, отражаемость слоя – Z ₁, скорость и направление ветра постоянны и равны соответственно V ₁ и γ ₁, ширина спектра скоростей σ ₁;

• –    второй слой: диапазон высот – от h ₁ до бесконечности, отражаемость – Z ₂, скорость и направление ветра в общем случае изменяются с высотой в соответствии с функциями V ₂( h ) и γ ₂( h ), ширина спектра скоростей – σ ₂.

Ширина спектра суммарного сигнала S ( w ), состоящего из двух составляющих S ₁( w ) и S ₂( w ), определяется формулой [4]

1 Г рр

^{О 2 =} P^, [ ^ ⁺ ^^{2 +} PPP ; ⁽ F 1 - ^F2 , ⁽¹⁾ где F ₁ и F ₂ – средние частоты, а P ₁ и P ₂ – мощности сигналов от первого и второго слоев соответственно.

На основе созданной численной модели принимаемого радиолокатором сигнала исследовано пространственное распределение ширины спектра для четырех характерных вариантов структуры приземного ветра.

Первый вариант метеообстановки – «скачок» вектора скорости – два слоя с разной отражае- мостью и разным направлением ветра в каждом из них.

В этом случае наибольшего значения ширина спектра достигает при равенстве мощностей отражений от обоих слоев и при азимуте антенны, на котором значение разности F ₁ – F ₂ максимально и _ соответствует вектору разности скоростей V 1 - V , (рис. 3).

ВЕСТНИК 2015

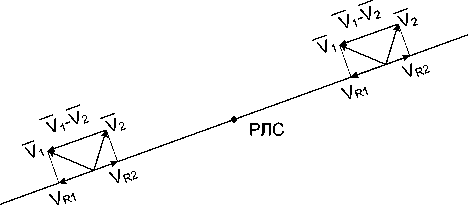
Рис. 3. Формирование максимума ширины спектра сигнала при «скачке» вектора скорости

Величины σ ₁ и σ ₂ можно оценить по отражениям от соседних элементов разрешения, в которых присутствует только один из слоев. Тогда сдвиг ветра ∆ V определяется по формуле

А V = V - V = - J 4с г ² - 2< г 2 - 2< г 2 ,     (2)

12 2         1    2

где V ₁ – скорость ветра в нижнем слое, V ₂ – скорость ветра в верхнем слое, с т - оценка величины σ , λ – длина волны.

Второй вариант метеообстановки – «сдвиг ветра без поворота».

Ветер во втором слое меняется с высотой по

закону

V 2 = V 1 + w ( h - h 1 ) , h >  h 1 .

Аппроксимируем поперечный разрез разрешаемого объема квадратом (рис. 4), равным по

Re площади кругу с радиусом r = -^- (6 - ширина

ДН антенны; R – наклонная дальность центра элемента разрешения).

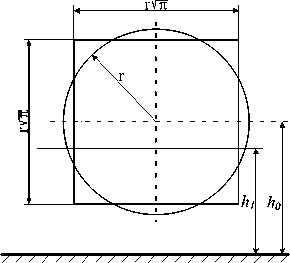
Рис. 4. Аппроксимация элемента разрешения

Второе слагаемое в формуле (7) имеет максимум только при условии ε > 1 (как правило, выполняемое), который достигается при нахождении x в интервале 0,95 ≤ x < 1, т.е. в случае, когда разрешаемый объем радиолокатора почти полностью «вышел» из нижнего слоя. Значение максимума невелико и не превышает 120% от той ширины спектра, которая обусловлена сдвигом ветра во втором слое. Следовательно, для оценивания величины W достаточно измерить ширину результирующего спектра на дальности, превышающей на 5% дальность расположения максимума. В этом случае ε = 0, x = 1 и из (7) по-

3 л a лучаем W = —-^.

Третий вариант метеообстановки – «поворот ветра без сдвига».

Направление ветра во втором слое меняется с высотой по закону

ВЕСТНИК 2015

Средняя частота спектра сигнала, отраженного вторым слоем, вычисляется по формуле:

h 0 + ^{rJ n}

F 2 = J f ( h ) p ( h ) dh ,        (4)

h 1

где f ( h ) – доплеровский сдвиг частоты, p ( h ) – распределение мощности отражений по высоте,

принимаемое равномерным, r – радиус поперечного разреза разрешаемого объема, h ₀ – высота центра элемента разрешения.

Ширина спектра сигнала, отраженного вторым слоем, вычисляется по формуле:

h 0 + r^

^{C 2} = J ( ^f ( ^h ) — ^F2 ) ² P ( ^h ) ^{dh .      (5)}

h 1

После вычисления формул (4), (5) и подстановки результатов в (1) получаем

γ ₂ = γ ₁ + ∆( h – h ₁), h ≥ h ₁. (8)

Как было показано в [3], показателем существования рассматриваемой метеообстановки служит появление на карте ширины спектра сигнала характерного распределения минимального значения измеряемого параметра в виде спирали. Следовательно, для оценивания скорости поворота ветра с высотой, надо найти формулу последней, т.е. зависимость дальности точки, в которой наблюдается минимум ширины спектра, от азимута антенны радиолокатора.

Используя принятую ранее аппроксимацию импульсного объема, находим среднюю частоту спектра сигнала, отраженного вторым слоем

r П ho + -y- f2 = J f (h) p (h) dh = h1

2V 1 cos ( a )

r V П

АЛ h 0 +—-—

^^^^^^e

×

r\Я sin ф - Y1 - A h0 +——

- sin ( ф - Y i ) . (9)

a2 = Г P . ^W\Y5>(PL+4Pil 1 , (6) Pi + P2 1 1     3Л2    (P1 + P2) r 'Jn

- h i .

Условием минимума σ ² будет

где A = h ₀ +

2 V

F ₂ = F = —1 cos ( ф - y ) ^cos ( a ) .

^{2     1} Л ^v

Обозначим

После ряда математических преобразований

приходим к выражению

₂ Pa ²    W² к r ²

a² = ^{1 1} +----—

P + P    3Л²

t = ^A h 0 +

V

r к

-

^ h i J ,

AZ где x = —-j= , e = — r dn     Z ₂

( e + ( 1 - e ) x ) 2

a = φ – γ ₁

и перепишем (9) с учетом (11) и (12). Получаем

.

sin ( a - 1 ) = t cos ( a ) + sin ( a ) .       (13)

Решить данное уравнение возможно только графическим способом [5]. Пример такого решения для a = 0,5 представлен на рис. 5.

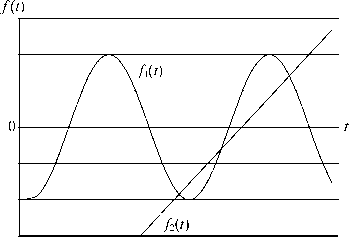
f 1 ( t ) = sin ( a - t ) , f 2 ( t ) = t cos ( a ) + sin ( a ) Рис. 5. Пример решения уравнения (12)

Четвертый вариант метеообстановки – «сдвиг ветра с поворотом».

Ветер во втором слое меняется с высотой по закону

V2 = (V1 + w(h - h))cos(y1 + A(h - h)), h > h1.                       (14)

Средняя частота спектра сигнала, отраженного вторым слоем, r \ П h +

F2 = J f (h) P (h) dh = h1

r 4П ^h 0⁺ —

= J h1

2 ( V₁ + W ( h - h ₁ ) )

cos

Гл It I

X h + ⁿ - h.

⁰        2          ¹ I

( ^ ^- ( Y 1 +^A ( h ^- h 1 ) ) ) dh .

Используя принятые ранее обозначения, получаем

2 V

F = —^L(sin ( a - t ) - sin ( a )) + ■

² A A X

2 W

+ A 2 AX ( t sin ( a - 1 ) + cos ( a ) cos ( a - 1 ) ) . (1

Минимум наступает при условии F ₂= F ₁. итоге приходим к выражению

WW sin (a -1)+     t sin (a -1)-     cos (a -1 ) =

V 5 V1A     V 7 VA

В

или

W

= t cos ( a ) + sin ( a )-JXA cos ( a )

, W V /   W  W   ,

1 + t sin ( a - t ) -     cos ( a - t ) =

VA J V    5 VA   V5

W

= t cos ( a ) + sin ( a )-"j7A cos ( a ) •

Пример графического решения данного уравнения представлен на рис. 6.

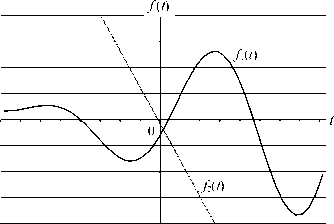
/1 ( t ) = | 1 +

W

--cos ( a - 1 ) ,

V1A    V ;

W f2 (t) = t cos (a) + sin (a) -'^Acos (a)

Рис. 6. Пример графического решения уравнения (16)

Заключение

Из приведенных расчетов следует, что получаемые современными метеорологическими радиолокаторами карты ширины спектра принимаемого сигнала несут информацию о распределении вектора скорости ветра по высоте в пограничном слое атмосферы. Характеристики этого распределения могут быть оценены по максимальному значению параметра на указанной карте и по образующейся зависимости его минимального значения от азимута антенны.