Обнаружение текстурных неоднородностей на микромасштабных изображениях материалов

Контроль качества является актуальной проблемой в области производства. В связи с этим первостепенное значение приобретает создание новых высокоинтеллектуальных методов контроля качества выпускаемой продукции взамен существующего трудоёмкого, дорогостоящего и субъективного метода визуального осмотра.

Так как текстура является одним из наиболее важных характеристик в выявлении дефектов, задача обнаружения дефектов в основном рассматривается как задача анализа текстурных изображений. В настоящее время методы текстурного анализа используются в промышленности для обнаружения дефектов многих поверхностей, таких как ткань, керамическая плитка, дерево, сталь, кремниевые пластины, бумага, кожа и т.д. Примеры текстурных изображений поверхности металла представлены на рис. 1.

б)

Рис. 1. Микроструктура поверхности металла: в исходном состоянии (а); с искажениями (коррозионное растрескивание) (б)

Можно выделить следующие методы текстурного анализа, используемые для выделения дефектов на изображениях: статистический подход, структурный подход, методы, основанные на фильтрации.

Среди статистических методов, применявшихся для обнаружения текстурных дефектов, следует выделить методы, основанные на гистограммах яркости [1], матрицах взаимного расположения [1- 3], локальных бинарных шаблонах и автокорреляционной функции.

Структурные методы для выявления дефектов на изображениях поверхности материалов были рассмотрены в работах Чена и Джейна [4]. В работе [5]

авторы используют морфологические операции для выделения дефектов на изображениях тканей.

Методы фильтрации, применяемые для выделения дефектов на изображениях, можно разделить на методы пространственной фильтрации, методы частотной фильтрации, использующие преобразование Фурье [6], и методы совместной пространственной и пространственно-частотной фильтрации, основанные на использовании фильтров Габора [7] и вейв-лет-преобразованиях [8].

Также хорошие результаты даёт использование авторегрессионных моделей [9], фрактальных моделей [10] и моделей Марковского случайного поля [11].

Следует отметить, что перечисленные выше методы обладают рядом недостатков. Так, например, автокорреляционный метод, структурные методы и методы фильтрации хорошо работают на регулярных текстурах (т.е. изображение состоит из повторяющихся элементов), однако обладают низкой эффективностью на нерегулярных случайных текстурах. Метод локальных бинарных шаблонов также показал низкую эффективность в ряде задач. Метод гистограмм обладает существенным недостатком: в нём используется предположение, что интенсивность в области дефекта должна отличаться от интенсивности в «нормальной» области. Для метода матриц взаимного расположения также следует отметить некоторые недостатки: так, не существует однозначного подхода к выбору вектора смещения, количество признаков велико, а значит, необходимо производить отбор признаков; метод не эффективен по сравнению с другими перечисленными методами.

В данной работе рассматривается так называемый метод обнаружения новизны (novelty detection [12, 13]) для выделения неоднородностей на текстурных изображениях. Данный метод заключается в построении функции, положительной в «нормальных» областях изображений, на которых неоднородности отсутствуют, и отрицательной в других областях. Данный подход позволяет выявить области изображения, отличающиеся от нормальных (неискажённых, однородных) областей. Отметим, что в отличие от классификации, где для обучения необходимо указывать искажённую и неискажённую об- ласти, метод обнаружения новизны требует только неискажённые области, что делает этот метод применимым в случаях, когда знание о модели искажения неполное или отсутствует совсем.

Модель изображения

Областью определения D изображения будем называть конечное, связное множество D с Z². Наиболее часто используются прямоугольный участок двумерной целочисленной решётки

D = L x х L y , (1) где L x , L y - соответственно высота и ширина изображения. Элементы области определения будем называть пикселями.

Под изображением будем понимать функцию

I : D ^ G , (2) где G - множество значений или множество цветов. Например, в случае полутонового изображения G = [0;1], для цветного RGB-изображения - G = [0;1]³.

Значение изображения I в пикселе p будем обозначать I p = I ( p ).

Для анализа текстурных изображений будем использовать модель Марковского случайного поля [14,15], т.к. эти методы оказались эффективными в задачах сегментации изображений, имитационного моделирования и т.д. [15-17].

Пусть S - конечное множество узлов (в случае изображений это область определения D ). Пусть Z = { Z 1 , — , Z m } - семейство случайных переменных, определённых на множестве S , каждая случайная переменная Z_v принимает значение z_v е G . Семейство Z будем называть случайным полем. Будем использовать обозначение Z_i = z_i для события, что Z_i принимает значение z_i , а для совместного события ( Z 1 = z 1 , " , Z m = z m ) будем использовать обозначение Z = z .

P ( Z = z_v ) - вероятность того, что случайная переменная Z_i принимает значение z_i .

Связь узлов друг с другом определяется системой окрестностей, которая определяется как N = { N s | s е S } , где N s - множество узлов соседей узла s . Окрестности обладают следующим свойством: s 6 N s . Окрестность называется симметричной, если выполнено условие: s е N_t тогда и только тогда, когда t е N s .

Примеры окрестностей показаны на рис. 2.

Случайное поле Z называется Марковским случайным полем (МСП) по отношению к системе окрестности N , если для любого z i е Z выполнено следующее условие:

P ( Z i lZ s / i ) = P ( Z i l z N ). (3)

Далее будем использовать следующие обозначения:

• •    N_p - окрестность пикселя p ;

• •    N pk - k -ый элемент окрестности;

• •    I n p = ( I ( N p ) , ... , I ( N p ) ) - вектор значе

ний отсчётов изображения в окрестности пикселя p .

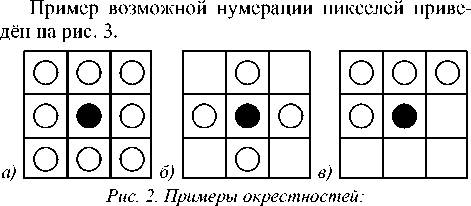
некаузальная (а); ближайший сосед (б); каузальная (в)

некаузальная (а); каузальная (б)

Каждое изображение, являющееся реализацией Марковского случайного поля с распределением P , можно рассматривать как реализацию многомерной случайной величины, которая обладает таким же распределением:

^{( Z} 0 , z^ " , z n ),                                        ⁽⁴⁾

где ^z 0 = I p , ^{( Z} 1^, " ^, z n ) = ^z = I n p .

Каждому изображению будет соответствовать конечное множество векторов окрестностей:

N ( I ) = { ( Z 0 , Z 1 , " , Z n ) } ,                              (5)

где ^Z 0 = I p , ^{( Z} 1^, " ^, z n ) = I N p , P ^{е L}x ^X L y .

Для анализа изображений можно использовать характеристики выборки окрестностей N ( I ).

Постановка задачи обнаружения текстурных неоднородностей

Непосредственным соседом (Н-соседом) [18] пикселя p будем называть пиксель p , который имеет с пикселем p общее ребро. Окрестность, состоящую только из Н-соседей пикселя p , будем считать Н-окрестностью пикселя p . Пример Н-окрест-ности представлен на рис. 2 б .

Связной будем называть область S , если для любых пикселей p_n , p m е S существует маршрут ( p 0 , p 1 , " p_k )^{е s} , такой, ^что p 0 = p_n , p_k = p m ^и

V i = 1, k , p, е N где N

‘            pl - 1                       p l - 1

Н-окрестность точ-

^ки P i - 1 ■

Будем рассматривать два типа изображений: изображения, не содержащие неоднородности, и изображения с неоднородностями.

Будем считать, что изображение, не содержащее неоднородностей, является реализацией Марковского случайного поля с распределением P ■

Неоднородностью на изображении I будем называть связную область, описанную некоторым, отличным от P , распределением вероятности P ■

Множество областей неоднородностей изображения I можно представить как объединение связ- n ных областей HI = ^ Si   при условии, что i=1

V i = 1, n , j = 1, n , S i и S j - несвязное множество и

Si n Sj =0 ■

Разрабатывается алгоритм, который данному изображению I ставит в соответствие бинарное изображение I , определённое следующим образом:

। = [ 0, p е H i ;

^P   [ 1,   p е H i ■

Иллюстрация данного алгоритма представлена на рис. 4.

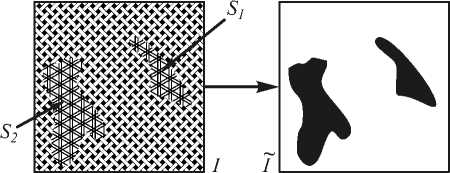
Рис. 4. Схема алгоритма обнаружения текстурных неоднородностей

Метод обнаружения текстурных неоднородностей

Пусть заданы изображение и соответствующая ему выборка векторов окрестностей, которая соответствует распределению P ■ Таким образом, пиксели, которые попадают в область дефекта, обладают вектором окрестности, вероятность которого мала^

Поэтому в основе метода выделения дефектов лежит подход разделения носителя плотности на две области: S и E = D \ S , причём P ( S ) >>  P ( E ) ■ Другими словами, множество S содержит наибольшую часть вероятности

Необходимо разработать алгоритм, вычисляющий бинарную функцию, выделяющую области на исходном изображении, где сосредоточена наибольшая в некотором роде плотность; т^ функция ненулевая в областях, где расположена большая часть векторов окрестностей

Для решения этой задачи в работе [19] был разработан метод обнаружения выбросов (или новизны)

Метод основан на построении бинарной функции f , которая принимает значение 1 на множестве S и - 1 - в противном случае^ Такая функция ищется в классе функций, допускающих представление в виде разложения по некоторому подмножеству векторов наблюдаемой выборки (называемых опорными векторами)

Важной частью представленного в работе метода является так называемый переход к ядру, который заключается в вычислении скалярного произведения в признаковом пространстве высокой размерности с использованием функции, определённой для пары входных образов^

Пусть X - некоторое множество^ Для простоты будем считать, что это компактное подмножество Ж N ■ Определим функцию ядра к , соответствующую скалярному произведению в признаковом пространстве высокой размерности H , через отображение Ф следующим образом:

Ф : X ^ H , (7)

x ^ x := Ф ( x ) , (8)

к ( x , x ') = (Ф ( x ) , Ф ( x ')} , (9) где x , x 'е X , ^Ф ( x ) , Ф ( x ')^ - скалярное произведение векторов Ф ( x ) и Ф ( x ‘ ) ■

Использование функции ядра позволяет нам для решения задачи обнаружения новизны построить поверхность решений (границу множества), которая во входном пространстве является нелинейной, однако её образ в признаковом пространстве будет являться линейным ■

Примеры построения таких пространств можно найти в [19,20] Преимущество метода заключается в том, что для работы необходимо знать только функцию к ■

Функция квантилей и множество минимального объёма

Введём понятие многомерной функции квантилей [17], Будем рассматривать выборку независимых одинаково распределённых случайных величин x 1 , ^ , x_n , x i е X с X с распределением P ■

Пусть C будет множеством измеримых подмножеств из X ■ Пусть % будет действительной функцией, определённой на C ■

Тогда функция квантилей относительно ( P , % , C ) будет определена как

U ( ц ) = inf{ % ( C ) | P ( C ) > ц , C е C },0 < ц < L (10)

Иначе говоря, функция квантилей - это мера того, насколько большое множество необходимо, чтобы охватить определённое количество вероятности распределения P ■

Обозначим за C % ( ц ) (или C m ( ц ) в эмпирическом случае) такое C е C , на котором достигается инфимум^

В данном методе в качестве % выбирают меру вида:

% ( C w ) = | Н |²,                                   (11)

где C w = { x\f w ( x ) >р ] и ( w , р ) - соответственно вектор весовых коэффициентов и смещение, описывающие гиперплоскость в пространстве признаков, связанном с ядром.

Метод обнаружения новизны

Рассмотрим обучающую выборку

X = {x1,_,Xm} с X.(12)

Чтобы отделить выборку от начала координат, решим следующую задачу квадратичного программирования:

min   —IIwl |2 + — У ^i-р we H,^eRm ,peB 2

при условии, что

( w, ф( x )}>p4 i , ^i > 0, где ve (0,1].

Так как фиктивные переменные £i накладывают штраф на целевую функцию, можно предположить, что если w и р являются решениями данной задачи, то пока регуляризационный параметр w будет мал, решающая функция f (X ) = sgn (( w, ф( X )^-р)                     (15)

будет равна 1 для большинства примеров x_i из обучающего множества.

На рис. 5 представлен пример гиперплоскости w , Ф ( x )^ = р с вектором-нормалью w и смещением р , отделяющей всё, кроме одной точки выборки, от начала координат. Выброс Ф ( x ) связан с фиктивной переменной £ , которая накладывает штраф на целевую функцию (13). Расстояние от выброса до гиперплоскости равно £ /11 w ||, расстояние от гиперплоскости до начала координат равно р /|| w ||. Из вышесказанного следует, что малое значение w соответствует большому расстоянию от начала координат до гиперплоскости.

Решающая функция в терминах ядра будет иметь вид:

f ( x ) = sgn I У a i k ( Xi , x ) -р1 ,                 (16)

\ i                    / где р = (w, Ф(xi )^ = У ajk (xj, xi).

Отметим, что в решении (16) часть коэффициентов a i будет равна 0. Вектора x i , для которых a i ^ 0 , называются опорными.

Более подробное обсуждение того, как решать задачу (13), (14), может быть найдено в [19].

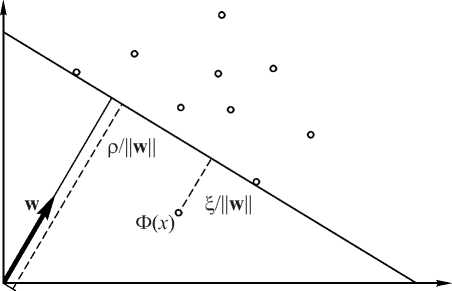
Рис. 5. Пример гиперплоскости, отделяющей выборку от начала координат

Следует отметить следующие свойства параметра v :

• v является верхней границей относительного числа выбросов – точек, лежащих с отрицательной стороны гиперплоскости;

• v является нижней границей относительного числа опорных векторов.

Детали реализации алгоритма

Пусть X = [0;1] ¹ , где 1 - размер окрестности (количество пикселей в окрестности, включая центральный, т.е. для некаузальной окрестности 3 х 3 l будет равно 9).

В качестве обучающего множества для метода (12) используется множество векторов окрестностей X = N ( I ).

В качестве функции ядра скалярного произведения будем использовать гауссово ядро:

k ( x , x ') = e ~^Y| x ^- x ¹ ^.                                        (17)

Экспериментальные исследования

Для проведения экспериментальных исследований были использованы натурные изображения микроструктуры поверхности материалов.

Общая схема экспериментальных исследований представлена на рис. 6.

Для исследования качества работы алгоритма и анализа текстурных изображений тестовые изображения зашумляются заранее известным способом. Зашумление анализируемых изображений производится путём врезки в изображение фрагмента другого изображения.

Результатом анализа изображения является бинарное изображение, на котором области чёрного цвета соответствуют найденным на изображении локальным неоднородностям.

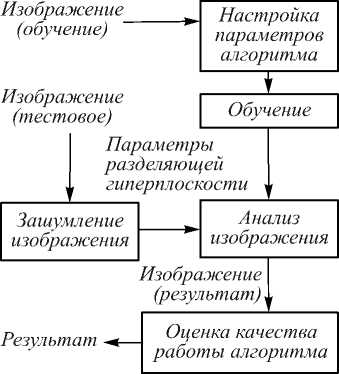
Рис. 6. Схема эксперимента

Далее по полученным бинарным изображениям определяется качество выделения локальных текстурных неоднородностей.

В качестве критериев качества выделения локальных текстурных неоднородностей будем использовать относительное число правильно классифицированных отсчётов q , ошибку первого рода p ₀ и ошибку второго рода p ₁ :

q = n , ⁽¹⁸⁾

n 0

p 0   N ’

n

pi = N

где n – число правильно классифицированных от счётов , n₀ – количество ложно обнаруженных от счётов , n₁ – количество пропущенных отсчётов , N – общее число отсчётов .

Возьмём в качестве обучающего и анализируе мого изображения фрагмент реализации двумерного пространственно - однородного ( стационарного ) слу чайного поля , описанного математическим ожида нием M_f и автокорреляционной функцией :

B ( т 1 , t₂ ) = D f exp ( a_xT 2 + T ) . (21)

В качестве искажения возьмём фрагмент реализации стационарного случайного поля, описанного той же автокорреляционной функцией, но с другими параметрами.

Результат работы алгоритма представлен на рис. 7. Результаты вычисления критериев качества выделения текстурных неоднородностей представлены в табл. 1.

Далее будем рассматривать текстурные изображения, сгенерированные по заданным образцам с использованием имитационного моделирования. В качестве образцов будем использовать натурные изображения микроструктуры поверхности металлов, представленные на рис. 8.

б)

Рис. 7. Экспериментальное исследование алгоритма: обучающее изображение (а); анализируемое изображение (б);

изображение результата v = 0,001, / = 10 (в)

Таблица 1. Критерии качества выделения текстурных неоднородностей

q	p 0	p 0
0,988	0,002	0,01

Рис. 9. Экспериментальное исследование алгоритма: обучающее изображение (а); анализируемое изображение (б); изображение результата v = 0,1, / = 10 (в); изображение результата v = 0,001, / = 10 (г)

Рис. 8. Примеры тестовых изображений

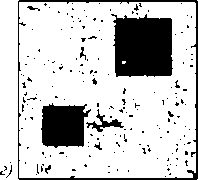
Результаты работы алгоритма представлены на рис. 9-10. Результаты вычисления критериев качества выделения текстурных неоднородностей представлены в табл. 2-3.

б)

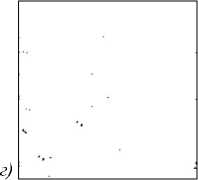
а)                           б)

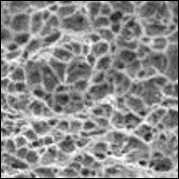
Таблица 2. Критерии качества выделения текстурных неоднородностей

V	Y	q	p 0	p 1
0,1	10	0,901	0,099	0
0,001	10	0,9986	0,0014	0

Таблица 3. Критерии качества выделения текстурных неоднородностей

V	Y	q	p 0	p 1
0,0039	600	0,96	0,036	0,004
0,0156	800	0,967	0,03	0,003

Рис. 10. Экспериментальное исследование алгоритма: обучающее изображение (а); анализируемое изображение (б);

изображение результата, V = 0,0039 у = 600 (в);

изображение результата V = 0,0156, у = 800 (г)

На рис. 11 представлен результат работы алгоритма в случае, если обучающее изображение содержит небольшое искажение.

Рис. 11. Экспериментальное исследование алгоритма: обучающее изображение (а); анализируемое изображение (б);

изображение результата V = 0,1, у = 5 (в)

Заключение

В данной работе был разработан метод выделения локальных текстурных неоднородностей, проведены исследования на тестовых и натурных изображениях.

Исследования показали, что для обучения можно использовать изображения, которые уже содержат неоднородности, что является преимуществом, т.к. большинство других методов требуют для обучения использовать неискажённые изображения.

Также исследовалось влияние параметров алгоритма на качество выделения текстурных неоднородностей. Исследования показали, что для качественного решения задачи выделения текстурных неоднородностей для изображений различных классов необходимо подбирать индивидуальные параметры алгоритма на основе максимизации относительного числа верно классифицированных пикселей по обучающему множеству изображений.

Следует отметить, что метод применим во многих других областях, таких как контроль качества выпускаемой продукции или диагностика заболеваний путём выделения нетипичных особенностей на медицинских изображениях.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), гранта Президента РФ поддержки ведущих научных школ (НШ-3086.2008.9), программы Президиума РАН «Фундаментальные науки – медицине», грантов РФФИ 10-07-00341-а и 10-07-00553-а, государственного контракта № 02.740.11.0841.