Обобщение понятия "прямая Эйлера" с треугольника на ортоцентрический тетраэдр

Треугольник, как кладезь прекрасных и поразительных геометрических конструкций, поистине неисчерпаем. Их пестрота и изобилие, с трудом поддающиеся какой-либо систематизации, не могут не восхищать. Красивая теорема в геометрии треугольника связана, как правило, с замечательными точками, прямыми или окружностями. Но прямая или окружность замечательна, если содержит какие-нибудь замечательные точки треугольника. В точки эти, стало быть, все и упирается.

При рассмотрении замечательных точек и других геометрических образов, связанных с треугольником, часто не удается сразу начертить треугольник, в котором замечательные точки достаточно далеко отстояли друг от друга. С целью облегчить построение такого треугольника Д. Саттерли предлагает несколько треугольников, размеры которых подобраны так, что замечательные точки и окружности хорошо выделяются. Рассмотрим такой «хороший треугольник».

Но сначала рассмотрим знаменитую теорему великого Л. Эйлера. Теорема: В треугольнике точка пересечения медиан, ортоцентр и центр описанной окружности лежат на одной прямой.

Доказательство: Проведем через вершины треугольника АВС прямые, параллельные сторонам треугольника, до их взаимного пересечения в точках А 1 , В 1 , С 1 . Тогда четырехугольники АВА 1 С, САС 1 В, АВСВ 1 – параллелограммы. Значит, ВС 1 = ВА 1 = АС. В 1 С = А 1 С = ВА.

Отрезки АА1, ВВ1, СС1 являются диагоналями этих параллелограммов и делят пополам стороны ВС, АС, АВ соответственно. Тогда эти отрезки пересекаются в точке М пересечения медиан треугольника АВС, и

МА/МА 1 = МВ/МВ 1 = МС/МС 1 = - ½.

Это значит, что при гомотетии с центром в точке М и коэффициентом k =-1/2 треугольник АВС переходит в треугольник А1В1С1. Данная гомотетия переводит центр О окружности, описанной около треугольника АВС, в точку Н, т.е. точки М, О, Н лежат на одной прямой. При этом точка М лежит между точками О и Н, и МН = 2МО.

Проверку теоремы удобно рассмотреть с помощью метода координат.

Возьмем начало координат в вершине А и примем прямую АС за ось абсцисс. Тогда А (0;0), С (168;0), В (120;90). Нетрудно будет вычислить центр тяжести М, центр описанной окружности О, центр вписанной окружности I, ортоцентр Н, центр окружности девяти точек О9, точку Фейербаха Ф.

Таб. 1.

А	В	С	М	О	I	Н	О 9
(0;0)	(120;90)	(168;0)	(96;30)	(84;13)	(108;36)	(120;64)	(102;38,5)

Ф	R	r	АВ	АС	ВС
(141,2;22,2)	85	36	150	168	102

Площадь треугольника АВС равна 1890. Ясно, что такой треугольник удобнее всего чертить на миллиметровой бумаге. Такой треугольник дает хорошую возможность проверки результата Л. Эйлера, что ортоцентр, центр описанной окружности и медиана треугольника лежат на одной прямой – прямой Эйлера. И более того, проверим, что НМ = 2ОМ.

Проведем векторную проверку теоремы Эйлера:

→   96 – 120    - 24

НМ = 30 - 64  =  - 34

242 + 342 = 4 (122 + 172);

→   84 – 96

МО = 13 - 30

- 12

- 17 отсюда имеем,

1732 = 1732, НМ = 2МО.

Здесь неожиданным является еще тот факт, что треугольники

АВН 2 – египетский (3;4;5), ВСН 2 – индийский (8;15;17)

АДН2 , АНН2 – индийский (8;15;17) , СДН2, СНН2 - египетский (3;4;5), и более того, если рассмотреть треугольники АНС, АНВ, ВНС, АВС, то радиусы описанных окружностей у них равны, в данном случае R = 170.

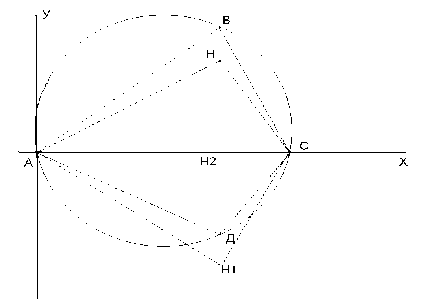
Рис. 1

Верно следующее суждение: всякий треугольник – ортоцентрический (т.е. во всяком треугольнике три высоты пересекаются в одной точке).

Однако не всякий тетраэдр – ортоцентричен. Четыре высоты лишь некоторых тетраэдров пересекаются в одной точке. Теорема интересна и продуктивна тем, что можно успешно обобщить понятие «прямая Эйлера» с треугольника на ортоцентрический тетраэдр.

Плоскость Пространство

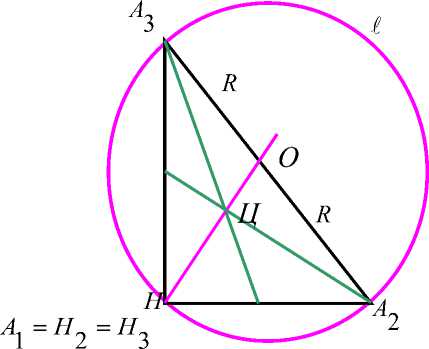
Рис. 2.

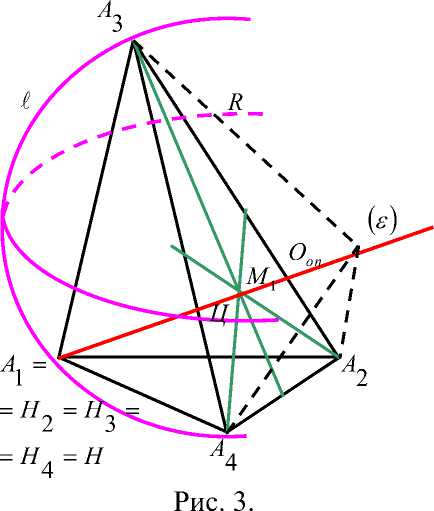
В качестве объекта испытания истинности теоремы удобно осуществлять проверку на эталонных фигурах, на которых быстрее можно получить числовые данные (или зрительно убедиться в истинности теоремы). Такой «эталонной фигурой» в пространстве служит равнобедренный прямоугольный тетраэдр. Построим в координатном пространстве равнобедренный прямоугольный тетраэдр А1А2А3А4, с координатами А1(0;0;0), А2(0;12;0), А3(0;0;12), А4(12;0;0). В равнобедренном прямоугольном тетраэдре боковые ребра – суть высоты, опущенные из трех вершин к противоположным граням; все четыре высоты равнобедренного прямоугольного тетраэдра пересекаются в одной точке (в начале координат). Н –ортоцентр тетраэдра, его координаты в данном случае Н(0;0;0). Найдем координаты Ц – центроида тетраэдра, как среднее арифметическое соответствующих координат вершин тетраэдра.

Ц Х = (х 1 + х 2 + х 3 + х 4 )/4 = (0 + 12 + 0 +0)/4 = 3, аналогично найдем следующие координаты и имеем Ц_х = Ц_у = Цz =3 и Ц (3;3;3). Найдем положение центра О сферы, описанной около равнобедренного прямоугольного тетраэдра А₁А₂А₃А₄. Так как точка О равноудалена от всех вершин, то точка О лежит на прямой О 1 Ц, где О 1 центр описанной окружности А 2 А 3 А 4 . Точка О лежит на симметрали бокового ребра А 1 А 2 , О(6;6;6). Теперь докажем, что Ц,О,Н лежат на одной прямой. Это очевидно из вычислений координат х = у = z. Мы успешно обобщили понятие «прямая Эйлера» с треугольника на ортоцентрический тетраэдр.

Аналогом треугольника на плоскости является тетраэдр. Прямые аналогии приводят к двум классам тетраэдров: ортоцентрических тетраэдров (все высоты пересекаются в одной точке) и равногранных (все грани – равные треугольники), представитель которых может служить пространственным аналогом правильного треугольника. Основные цели задания состоят в получении различных (но эквивалентных) критериев для этих двух классов тетраэдров.