Обобщение принципа спектроскопического соответствия на временную зависимость квантовых переходов
Автор: Астапенко В.А., Сахно С.В., Сахно Е.В.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Физика
Статья в выпуске: 1 (49) т.13, 2021 года.
Бесплатный доступ
Обобщается общеизвестный принцип спектроскопического соответствия для временной зависимости квантовых переходов путем сравнения зависимости энергии электромагнитного импульса от времени, поглощаемого двухуровневой системой и классическим линейным осциллятором. Формулы для зависимостей, упомянутых выше, получены для двух случаев: систем с релаксацией и без нее. Показано, что в первом случае результаты для квантовых и классических систем в точности совпадают. Если релаксация достаточно велика, заметна разница между двумя временными зависимостями поглощенной энергии.
Принцип спектроскопического соответствия, квантовый переход, двухуровневая система, классический линейный осциллятор
Короткий адрес: https://sciup.org/142230101
IDR: 142230101 | УДК: 535.3
Текст научной статьи Обобщение принципа спектроскопического соответствия на временную зависимость квантовых переходов
Спектроскопический принцип соответствия между классическим и квантовым подходом в описании взаимодействия между электромагнитным полем и атомом заключается в следующем [1]: атом представляется в виде набора, классических осцилляторов (т.н. осцилляторов перехода), отвечающих дипольно-разрешенным переходам между состояниями дискретного спектра. Собственные частоты этих осцилляторов равны боровской частоте перехода, между заданными состояниями, а. отклик на. электромагнитное воздействие пропорционален безразмерной величине - силе осциллятора, перехода. С помощью принципа. соответствия можно количественно описать ряд важных радиационных процессов и атомных характеристик, не прибегая к формализму квантовой механики. Так, например, выводится выражение для динамической поляризуемости атома. [2], а. также формулы для
«Московский физико-технический институт (национальный исследовательский университет)», 2021
сечения рассеяния света [3] и для сечения фотопоглощения излучения в дискретном атомном спектре.
Более общий принцип соответствия между классической и квантовой механикой состоит в следующем: квантово-механические формулы получаются из классических, если в последних фурье-образы физических величин заменить на матричные элементы операторов, отвечающих данным величинам, вычисленных на частотах, равных частотам переходов между квантовыми состояниями [4].
Оба вышеуказанные принципа не рассматривают временной зависимости квантового перехода, которая в настоящее время становится физически измеримой величиной в связи с развитием экспериментальных методов аттосекундной физики, таких как: selfreferenced attosecond photoelectron interferometry [5], an interferometric technique combining high temporal and spectral resolution [6], the combination of transient absorption and ion mass spectroscopy with attosecond resolution [7].
Экспериментально и теоретически исследуются следующие фотопроцессы с аттосекунд-ным временным разрешением: фотоионизация хиральных молекул [5], атомов гелия [8], неона [6] и криптона [7], динамика электронов в многоэлектронных атомах [9], динамика фотовозбуждения атома водорода [10], динамика формирования резонанса Фано [11-13].
Вследствие этого обобщение принципа соответствия между классической и квантовой физикой на временную зависимость квантового перехода становится актуальным вопросом, которому и посвящена данная работа.
2. Обобщение принципа спектроскопического соответствия для временной зависимости квантовых переходов
Рассмотрим принцип соответствия путем сравнения временной зависимости энергии ЭМИ, поглощенной классическим осциллятором — Ec i as(t), и осциллятором перехода в квантовой двухуровневой системе — E9tomt(t) к заданному моменту времени t. Полагаем, что классический осциллятор имеет элементарный заряд и массу, равную массе электрона. Для простоты считаем, что сила осциллятора ДС равна единице: /о = 1.
В атомных единицах ~ = е = те = 1 для энергии ЭМИ, поглощенной классическим осциллятором к моменту времени t, имеем (см. Приложение 1):
Г Г dw'. гш' exp(-iw't')
dtE (t')v(t')= dt Е (t ) —E (ш ) —--- 2 , . 1
J J 2тт w'2 - ш0 + 2гш'у
-∞ -∞ -∞
Здесь E (t') — напряженность электрического поля в ЭМИ, E(w' ) — его фурье-образ, шо — собственная частота классического осциллятора, равная частоте перехода в ДС, у — константа релаксации классического осциллятора, равная спектральной ширине линии в ДС, v(t') — скорость осциллятора в заданный момент времени. Предполагается, что E(t ^ —то) = 0 и e(t ^ —то) = 0 для классического осциллятора и ДС. Отметим, что интеграл по частоте в правой части равенства (1) представляет собой скорость классического осциллятора в момент времени t'.
Для энергии, поглощенной квантовой ДС к заданному моменту времени, можно получить в рамках первого порядка теории возмущений следующее выражение:
∞
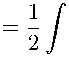
t
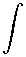
E(t ) exp(iw't' )dt'
∞
-
где G(w' ) — спектральная форма линии дипольно-разрешенного перехода в ДС. Формула (2) выводится аналогично тому, как это было сделано в статье [10] при выводе вероятности возбуждения радиационного перехода между состояниями дискретного спектра (см. Приложение 2).
3. Предел больших времен
Получим сначала выражения для поглощенной энергии за все время действия импульса при t ^ то. Физически данное условие соответствует временам, много большим длительности ЭМИ. В квантовом случае возбуждения ДС результат непосредственно вытекает из формулы (2):
eq uant (t ^^j du'С(ш') \Е(ш' ) I2 . (3)
Выражение для энергии, поглощенной классическим осциллятором за все время действия импульса, следует из (1). После ряда алгебраических преобразований имеем
∞
/ dш' ,
2_ \ е (ш )\
(ш '2
-
4ш'2 7 ш0)2 + 4ш '272
Заметим, что формулы (3) и
(4) совпадают, если форма линии в выражении (3) равна
̃︀
GO sc (w) /9
Г (ш0
-
4ш27
ш2)2 + 4ш272
Функцию Gosc(w) назовем осцилляторной формой линии. В пределе
7 << ш0
Gosc(w) совпадает с лоренцевской формой линии
С ь ^ш) — --— Г (шо
-
7___
ш)2 + 72 .
Как известно, форма линии (7) отвечает однородному уширению спектральной линии, вызванному, например, спонтанным излучением. Таким образом, имеется соответствие между энергией, поглощенной классическим осциллятором за все время действия ЭМИ, с энергией, поглощенной квантовой ДС, а именно: эти энергии совпадают, если выполняется условие (6). Заметим, что в случае возбуждения переходов в дискретном атомном спектре неравенство (6) выполняется с большим запасом. Так, например, для перехода ls~2p в атоме водорода, когда ширина линии обусловлена спонтанным излучением, отношение шо/7 та 107.
4. Случай отсутствия релаксации/нулевой ширины спектральной линии (у = 0)
Получим из (1) формулу для поглощенной классическим осциллятором энергии в случае 7 — 0. Выражая согласно определению фурье-образ напряженности электрического поля через функцию E(t), имеем dш' іш' exp(—іш'(t’ — t'')) 2г ш 2 — ш0 — 2іш'7
E clas (t) — j dtE (t') У dtE(t ') J
-∞ -∞ -∞
Интеграл по частоте в правой части равенства (8) можно вычислить с помощью теоремы о вычетах. В пределе 7 ^ 0 этот интеграл равен
7 dш' іш' exp(—іш'(t' — t' '))
— 6(t — t' ') cөs[шо(t' — t'')] ,
J 2 г ш2 — ш0 — 2іш'7
-∞ где Ө(т) — тета-функция Хэвисайда.
Подставляя правую частв равенства (9) в формулу (8), находим
Ed as (t) = / dt'E(t’) J dt" E (t‘‘)cos[ Ш0(t' - t’’)] =
-∞-∞
= 2 J dt'E(t') J dt"E(t") cos[ ш0(^ — t")] =ДО)
-∞-∞
t
= 2 J dt'E(tr) ехр(гш0Е) .
-∞⃒
При переходе ко 2-му равенству в (10) было использовано то обстоятельство, что подынтегральная функция симметрична относительно перестановки переменных интегрирования: t‘ О t’’.
В квантовом случае, в пределе у ^ 0, спектральная форма линии становится равной дельта-функции Дирака:
G b (y ^ 0) ^ Дшо — ш). (11)
Подставляя (11) в (2), получаем
E quant //)
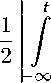
E (t‘) exp(гшot,)dt,
Из сравнения формул (10) и (12) следует, что в пределе нулевой ширины линии (для ДС) или в отсутствие релаксации (для классического осциллятора) выражения для временной зависимости поглощенной энергии ЭМИ в классическом и квантовом случаях совпадают.
5. Временная зависимость поглощенной энергии в общем случае (у = 0)
Проведем в общем случае (у = 0) численное сравнение временной зависимости энергии, поглощенной классическим осциллятором (по формуле (1)) и квантовой ДС (по формуле (2)) для ЭМИ с гауссовской огибающей:
E(t) = E0 exp(—t2/2т 2)cos(шt).
Здесь E o ,t и ш - амплитуда, длительность и несущая частота ЭМИ.
Рассмотрим возбуждение ДС с двумя формами спектральной линии (5) и (7). В расчетах полагаем, что Eo = 0.03, шо = 0.375. Данное значение собственной частоты отвечает переходу ls-2p в атоме водорода (в атомных единицах).
Результаты вычислений приведены на рис. 1-4 для различных констант релаксации у и параметров ЭМИ.
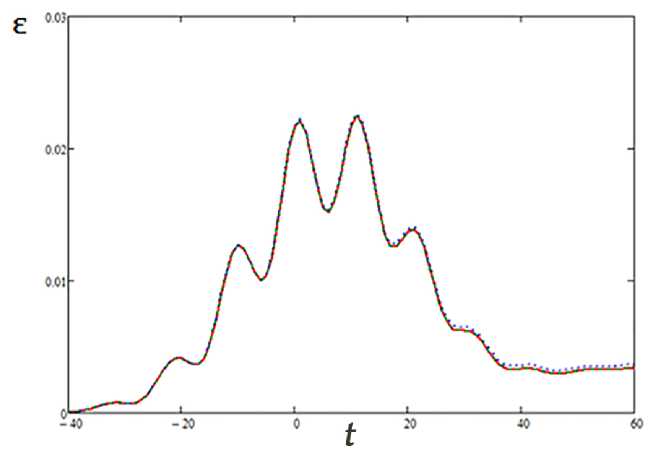
Рис. 1. Временная зависимость поглощенной энергии ЭМИ: сплошная кривая - для классического осциллятора, пунктир - для ДС с лорепцевской формой спектральной линии, штриховая кривая -для ДС с «осцилляторпым» профилем спектральной линии; 7 = 10 3,_- = 0.25,т = 20
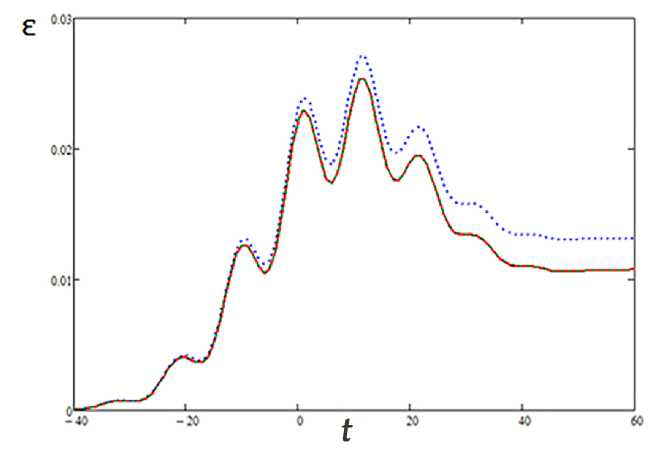
Рис. 2. Временная зависимость поглощенной энергии ЭМИ: сплошная кривая - для классического осциллятора, пунктир - для ДС с лорепцевской формой спектральной линии, штриховая кривая -для ДС с «осцилляторпым» профилем спектральной линии; 7 = 10 2,_- = 0.25,т = 20
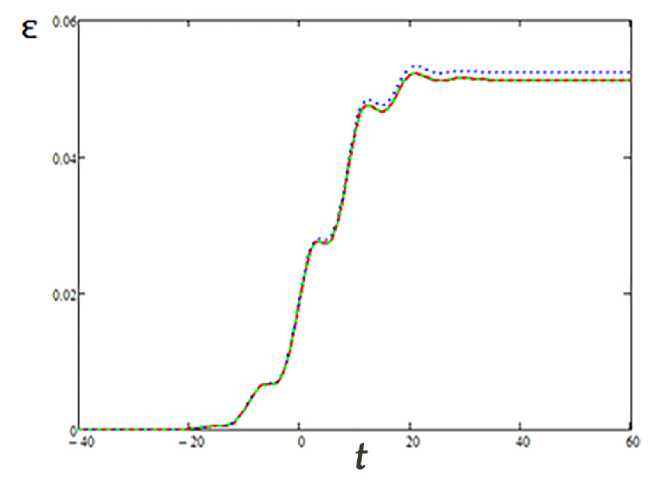
Рис. 3. Временная зависимость поглощенной энергии ЭМИ: сплошная кривая - для классического осциллятора, пунктир - для ДС с лорепцевской формой спектральной линии, штриховая кривая -для ДС с «осцилляторпым» профилем спектральной линии; 7 =10 2 ,ш = 0.25,т = 8
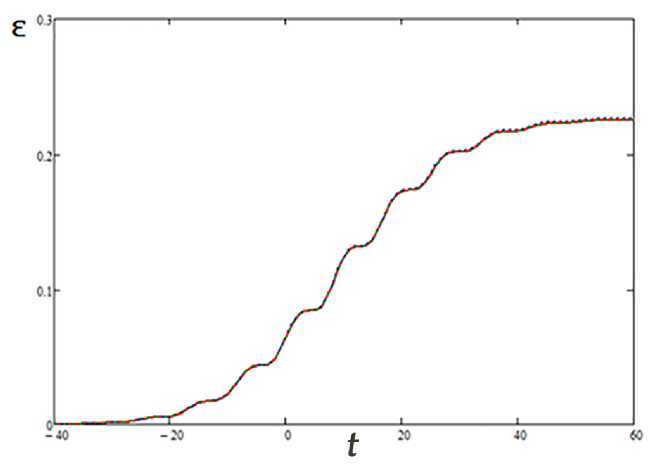
Рис. 4. Временная зависимость поглощенной энергии ЭМИ: сплошная кривая - для классического осциллятора, пунктир - для ДС с лорепцевской формой спектральной линии, штриховая кривая -для ДС с «осцилляторпым» профилем спектральной линии; 7 = 10-2, ш = 0.35,т = 20
Из приведенных рисунков видно, что для достаточно малых констант релаксации/ширин линии — 7 < 10-3 — все три кривые практически совпадают. Для больших значений 7 возникает отличие временной зависимости поглощенной энергии ДС с лорен-цевским контуром от двух других кривых. Это различие тем больше, чем больше отстройка несущей частоты ЭМИ от собственной частоты системы и уменьшается с укорочением ЭМИ. Кривая, соответствующая «осцилляторному» спектральному контуру всегда совпадает с кривой для классического осциллятора.
Приложение 1
Для энергии ЭМИ, поглощенной классическим осциллятором к моменту времени t, имеем
t
E clas (t) = j x(t")E(t')dt . (1.1)
-∞
Решение уравнения для гармонического осциллятора имеет следующий вид (см., например, [14]):
Г~ E(w')exp(-iw't) dw'
X(t) = У-^ w2 - w' 2 - 2i7w' 77'
Из формулы (1.2) вытекает выражение
. Г w'E(w') exp(-iw't) dw'
(1.3)
(1.4)
X(t) = -\ /-^ w2 - w'2 - 2i7w' 27*
Подставляя формулу (1.3) в (1.1), получаем
Eclas(t) = / dt'E (t') У
-∞ -∞
dw' , , iw' exp(-iw't') 2л w'2 - w2 + 2iw'7
Приложение 2
Вероятность фотовозбуждения в заданный момент времени под действием поля Е (t) (предполагаем, что Е (t ^ ±то) = 0 в дипольном приближении и первом порядке теории возмущения) имеет следующий вид [15]:
W (t) = j dt' j dt' ' Угловые скобки обозначают усреднение по начальному состоянию мишени. В формуле (2.1) используется коррелятор дипольных моментов (КДМ), который для стационарной системы может быть представлен в виде [16]: Подставляя (2.2) в (2.1), получаем W(t) = j dt' j dt"K(t'' - t')E(t')E(t'').(2.3) Фурье-образ КДМ имеет следующий вид [16]: К(t" - t')= / — exp(-iw(t" - t'))K(w). ( 2.4) -^ 27 Далее используем связь КДМ с сечением фотовозбуждения [16]: с . . К (w) = 2Tw^(w). Применяя простые преобразования: W(t) = I dt' I dt" I dw exp(-iw(t' - t'')) E(t')E(t'') ( 2.6 ) 4л2w -∞ -∞-∞ И W (t) = ср 4^2 Уо ш f dt' J dt” exp(—ішр — t'))E(t')E(t''), (2.7) получаем следующую формулу: W (t) = ∞ (Іш^Л ш г t 2 ' exp(ішt')E (t')dt' -∞⃒ (2.8) Из формулы (2.8) следует выражение для дифференциальной вероятности поглощения, которая обусловлена монохроматической составляющей на частоте ш: dW(t) с Дш) Г1 „ , , — = —---- exp(ішt')E (t)dt' dш 4^2 ш Loo Для дифференциальной энергии, поглощаемой на частоте ш, имеем de = dW dш dш Тогда для полной энергии получаем e =/ Дш = dш dш (2.9) (2.10) (2.П) Далее, в формулу (2.11) подставляем (2.9), при этом учитываем явное выражение для сечения фотовозбуждения мишени Дш) [16]: ст(ш) =----С(ш), с (2.12) где С(ш) - спектральная форма линии. Тогда получаем итоговую формулу: 1 Г Equant(t) = X I dш С(ш ) 2 0 Г t 2 ' E(t') exp(іш't')dt' -∞ (2.13) Заключение Таким образом, на примере исследования временных зависимостей поглощения энергии ЭМИ классическим осциллятором и квантовой ДС показано, что с точностью до учета различия формы спектральной линии (существенной только для больших констант релаксации) эти зависимости совпадают. Тем самым принцип соответствия между классической и квантовой физикой обобщен на временную эволюцию квантового перехода. Другой важный вывод из проведенных расчетов заключается в том, что для больших частотных отстроек и длинных импульсов временная зависимость поглощенной энергии имеет форму кривой с явно выраженным максимумом. В противоположном пределе максимум исчезает, и временная зависимость становится монотонной. Качественно наличие максимума во временной зависимости поглощенной энергии можно объяснить тем, что при больших частотных отстройках и длинных импульсах электромагнитное поле и осциллятор в течение второй половины длительности импульса колеблются в противофазе, так что поле тормозит осциллятор, и его энергия уменьшается. Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-07-00235 А.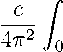
Список литературы Обобщение принципа спектроскопического соответствия на временную зависимость квантовых переходов
- Bohr N., Kramers H.A., Slater J. С. The Quantum Theory of Radiation // Phil. Mag. 1924. V. 47. P. 785-802.
- Kramers H.A. The law of dispersion and Bohr's theory of spectra // Nature. 1924. V. 113. P. 673-676.
- Kramers H.A., Heisenberg W. Uber die Streuung von Strahlung durch Atome // Zeitschrift für Physik. 1925. V. 31. P. 681-708.
- Rosmej F.В., Lisitsa V.S., Astapenko V.A. Plasma Atomic Physics // Springer, Springer Series on Atomic, Optical and Plasma Physics. 2020. V. 104.
- Beaulieu S., Comby A., Clergerie A. [et al.\. Attosecond-resolved photoionization of chiral molecules 11 Science. 2017. V. 358. P. 1288-1294.
- Isinger M., Squibb R.J., Busto D. [et al.\. Photoionization in the time and frequency domain // Science. 2017. V. 358. P. 893-896.
- Hütten К., Mittermair M., Stock S. [et al.\. Ultrafast quantum control of ionization dynamics // EPJ Web of Conferences. 2019. V. 205. 06001.
- Argenti L., Pazourek R., Feist J. [et al.\. Photoionization of helium by attosecond pulses: Extraction of spectra from correlated wave functions // Physical Review. 2013. V. 87. 053405.
- Nicolaides C.A. Attosecond-Resolved Electron Dynamics in Many-Electron Atoms: Quantitative Theory and Comparison with Measurements // Appl. Sei. 2018. V. 8. 533.
- Астапенко В.А. Аттосекундная динамика фотовозбуждения атома водорода ультракороткими лазерными импульсами // ЖЭТФ. 2020. Т. 157. С. 67-73.
- Golovinski P.A., Yakovets А. V., Astapenko V.A. Linear build-up of Fano resonance spectral profiles // Applied Physics B. 2018. 124:111.
- Kaldun A., Blättermann A., Donsa S. [et al.\. Observing the ultrafast buildup of a Fano resonance in the time domain // Science. 2016. V. 354. P. 738-740.
- Gruson V, Barreau L., Jimenez-Galan A. [et al.\. Attosecond dynamics through a Fano resonance: Monitoring the birth of a photoelectron // Science. 2016. V. 354. P. 734-737.
- Astapenko V.A. Interaction of Ultrashort Electromagnetic Pulses with matter. Springer, 2013.
- Клышко Д.Н. Фотоны и нелинейная оптика. Москва : Наука, 1980.
- Astapenko V.A. Simple formula for photoprocesses in ultrashort electromagnetic field // Physics Letters A. 2010.


