Обобщенная динамическая теория измельчения частицы твердого вещества импульсно-силовым сжатием двумя недеформируемыми шарами

PNRPU MECHANICS BULLETIN

На сегодняшний день повышение эффективности процесса измельчения материалов является одним из актуальных вопросов во многих сферах производства. Несмотря на широкий ассортимент существующих конструкций измельчительных машин, принципиально отличающихся друг от друга спецификой измельчения, потребность в совершенствовании последних остается на прежнем уровне [1]. Прежде всего это связано с современной тенденцией к миниатюризации, идея которой заключается в нанотехнологическом открытии и исследовании совершенно новых свойств наночастиц веществ.

В связи с этим возросли и требования к проектируемым измельчительным машинам. С одной стороны, конструируемая технологическая машина должна обеспечивать необходимый минимальный размер так называемой «частицы-продукта» (т.е. конечный размер частицы после помола), а с другой – обладать высокой энергоэффективностью и производительностью.

Данный подход поставил перед проектировщиками измельчительной техники ряд новых перспективных задач, связанных не только с обеспечением процесса измельчения как такового, но и с созданием инновационных машин, позволяющих адаптировать режим дроб- ления к конкретному измельчаемому материалу с учетом особенностей его физико-механических свойств.

Поставленная задача требует разработки соответствующего математического аппарата (метода расчета) для определения фактического значения прилагаемой нагрузки, необходимой для разрушения материала, от которой, в свою очередь, зависит энергоемкость процесса измельчения. При этом следует учесть ряд индивидуальных параметров обрабатываемого материала, связанных с исходным размером частиц, их прочностными свойствами, условиями разрушения и т.д.

Одним из прогрессивных направлений совершенствования процесса измельчения является разрушение твердого вещества посредством многократного приложения силы переменной (периодической) величины [2– 8]. Известно, что при циклической нагрузке разрушение материала возможно и в основном реализуется при напряжениях ниже предела текучести [9] в области упругих деформаций [10]. Можно констатировать, что эффективность применения данного принципа усиливается при использовании в процессе дробления мелющих тел, имеющих, как правило, сферическую форму. К таким машинам-измельчителям относятся шаровые, вибрационные, бисерные, планетарные и другие мельницы [1], в которых помол материала происходит при его интенсивном контактном взаимодействии с мелющими телами-шарами, выполняющими функцию передатчика потенциальной энергии разрушения частицам измельчаемого вещества. Количество энергии, требуемой для измельчения камня до определенного размера, зависит от размера, формы, взаимного расположения частиц, прочности, хрупкости, однородности, изотропности исходного материала и т.д. Поэтому установить аналитическое соотношение между энергоемкостью и механическими характеристиками измельчаемого вещества можно лишь приближенно. Следует также отметить, что движение мелющих шаров осуществляется в довольно сложном (хаотичном) режиме. Эти обстоятельства создают определенные трудности для разработки соответствующей механико-математической модели, позволяющей достаточно точно и адекватно оценивать напряженно-деформированное состояние и прочность твердого хрупкого вещества при его разрушении в процессе измельчения, зависящем от многих факторов случайного характера, трудно поддающихся расчету [10– 13]. Сложность процесса помола, исключающая возможность создания единой универсальной теории, привела к появлению общепринятых гипотетических предпосылок о замене действительных кусков материала самой разнообразной формы идеализированными расчетными схемами кубического или шарообразного вида [10]. Как показал анализ экспериментально-теоретических исследований в этой проблемной области, наблюдается отсутствие конкретных физико-математических зависимостей, реалистично аппроксимирующих процесс измельчения [1, 10].

Представленная статья посвящена математическому описанию процесса помола невесомой сферической модели частицы измельчаемого хрупкого материала радиусом R [10] путем ее соударения с шарообразными абсолютно твердыми телами большого радиуса R >>  R и массой m (рис. 1). На механическую систему, изображенную на рис. 1, действуют в противоположных направлениях некоторые внешние уравновешенные массы m , имеющие заданную скорость υ в начальный момент времени t = 0 , предшествующий присоединению m к m .

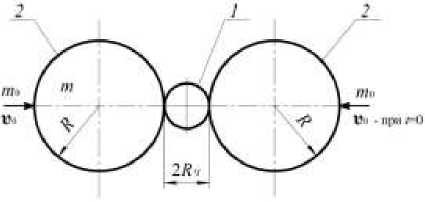
Рис. 1. Общая расчетно-конструктивная модель взаимодействия разрушаемой частицы 1 с шарами-измельчителями 2

Fig. 1. General computational and constructive model of interaction of the destroyed particle 1 with the grinding balls 2

Исследование ударных процессов относится к числу наиболее востребованных практикой фундаментальноприкладных разделов сопротивления материалов и тео- ретической механики, посвященных оценке поведения различных конструкций в условиях интенсивного силового воздействия импульсного характера. Такие динамические нагрузки имеют место при эксплуатации многих современных сооружений, машин, механизмов и приборов [14–16].

Сформулированный в названии статьи вопрос является предельным частным случаем [14] конструктивнонелинейной [17] задачи механики сплошной твердой среды об ударно-силовом контактировании двух шаров [15, 18, 19], движущихся вдоль оси, соединяющей их центры, со скоростями υ и υ после их точечного соприкосновения. В ее основе – классическая аналитическая зависимость Герца-Штаермана [18, 20] о реактивной статической нагрузке P , возникающей между сферическими телами, когда Uj = и₂ = 0 (рис. 2):

4 f 1 - ц 2   1 - н 2 Т* f R R 2 ) ²

P = — —-— +—-—  ■

• ³    I E 1      E 2   ) I ^R1 + ^R 2 )

  ■ u 2 ,

  
  
  
  

где R , R – радиусы шаров; u – сближение взаимодействующих тел в результате их локальной (контактной) деформации; μ , μ , E , E – соответственно коэффициенты Пуассона и модули упругости контактирующих материалов.

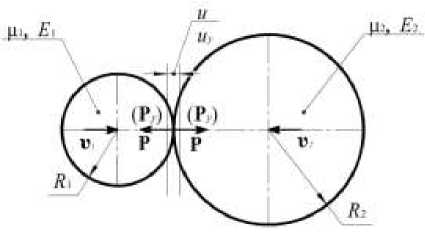
Рис. 2. Классическая схема соударения шарообразных элементов по Герцу [18–21]

Fig. 2. The classical scheme of the spherical elements collision according to Hertz [18–21]

В известной фундаментальной теоретической публикации [18] Г. Герц высказал основополагающее предположение, подтвержденное экспериментальной проверкой [14, 15, 22], что «комбинируя статическое сжатие в частях тел, лежащих непосредственно у места соприкосновения, с общими уравнениями движения для остальных частей тел, мы, вероятно, могли бы получить закон для соударения тел любой формы». В то же время следует учитывать в настоящее время тот очевидный факт, что точная теория удара, основанная на местных деформациях и колебательно-волновом распространении напряжений в упругом теле, оказывается пока еще очень сложной задачей [15, 21]. Поэтому ниже излагается прикладная математическая модель ударносилового импульса, возникающего в контактирующих шарообразных элементах (см. рис. 1).

Принимая во внимание допущение о недеформиру-емости мелющих шаров, а также симметрию и буквенные обозначения схемы рис. 1, представляем формулу (1) в более компактном упрощенном виде:

⁴ E  f ^R ч ■ ^R ) ² J

P                           z u ,

3 (1 - н2)( R + R J

после выполнения замен

R = R ₄, R = R , н = н, E i = E , E 2 = » ,    (3)

где μ , E – упругие постоянные измельчаемой частицы.

На рис. 3 дана конкретизированная схематизация процесса помола, адаптированная к решению поставленной динамической контактной задачи теории упругости, базирующейся на соотношении (2) и модели рис. 1.

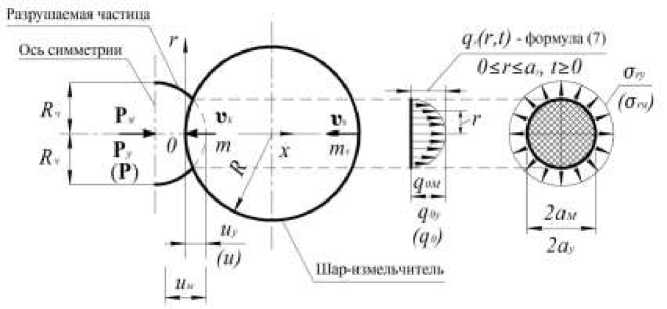
Рис. 3. Уточненное моделирование соударения шаров Fig. 3. Detailed modeling of ball collisions

В основе рассматриваемой теории измельчения используем теорему об изменении кинетической энергии движущейся со скоростью υ массы m [15, 24], формулу (2) и следующие классические предпосылки [15, 18, 22, 24]:

• а)    материал измельчаемой частицы – однородный, сплошной, изотропный и физически линейный, т.е. подчиняется закону Гука [17, 23, 25], а его прочностные свойства соответствуют хрупкому напряженному состоянию с разными временными сопротивлениями при сжатии g_bc и растяжении G_Bp <<  g_bc [25, 26], что характерно, например, для мрамора, гранита, песчаника и т.п. [26, 27];

• б)    соударяющиеся поверхности предполагаются совершенно гладкими [15];

• в)    удар является неупругим при нулевом коэффициенте восстановления [24, 28];

• г)    характер аналитических соотношений между усилиями P , P_y = P_y ( t ) и перемещениями u , u = u _y ( t ) остается неизменным при статической P и динамической P_y ( t ) силах, где t - время, т.е. (рис. 3)

д) физико-механические характеристики μ , E из-

мельчаемого вещества остаются постоянными в условиях динамического нагружения, что допустимо для ско-м ростей соударения и0 < 100 — [22];

с

• е)    установлено [14, 22], что вибрации и колебания, возникающие в движущемся шаре при ударе, не оказывают заметного влияния на его продолжительность t и на величину напряжений в материале;

• ж )    время t M = 0,5 1 _y завершения активной фазы ударного импульса (рис. 4) [22] адекватно моменту достижения наибольшей абсолютной динамической деформации u_M = u _y ( t_M ) (рис. 3), соответствующей, в свою очередь, скорости перемещения суммарной массы m₀ + m :

и = и (tM ) =

du

^dt J t = t..

M

= 0,

Pу = Py (t ) =

4 E     f R ■ R ) ²    3

ч 2

3 ■(I - н2) ( R + R J uy

иными словами, в случае t = t_M реактивная продольная сила удара

^P y ( t M ) = ^P M = max , ⁽⁶⁾ а при t >  t _y равнодействующая P_y = P_y ( t ) эллиптической функции контактного давления [9, 10]

а стационарная функция P = P ( u ) выражается формулой (2);

q y = q y ( r , t ) = q 0

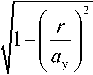
, 0 <  r <  a y , 0 <  t <  t y   (7)

с экстремумом

q oy = q o y ( 0, t ) = _y .                    ⁽⁸⁾

2πa в центре r = 0 круговой площадки (на рис. 3 она заштрихована) радиусом aу << R , ^ uу << Rч             (9)

становится равной нулю ( Р_у ( t ) = 0, t ^ t _y, рис. 4);

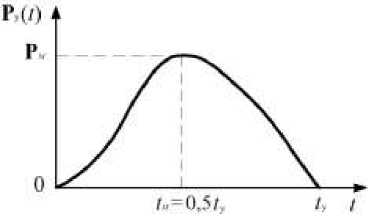
Рис. 4. Обобщенный вид графика ударно-силового импульса Fig. 4. Generalized view of the pulse-force pulse graph

• з)    пренебрегаем собственным весом G₄ частицы, по сравнению с весовой составляющей G >>  G₄ шара-измельчителя (при R >>  R );

• и)    в процессе математической аппроксимации напряженного состояния разрушаемого материала учитываются только местные (контактные) деформации, и это допущение является обоснованным, с общепринятой в настоящее время точки зрения, применительно к сферической модели (рис. 1–3) [14, 15, 18, 22];

• к)    определяющим фактором при оценке общей несущей способности шаровой расчетной схемы измельчаемой частицы из хрупкого вещества согласно [21] является наибольшее главное σ растягивающее напряжение:

° r y = ° 1 =        q 0у , ⁰ ^ t ^ t M ,            ⁽¹⁰⁾

действующее в радиальном направлении на круговой границе поверхности контакта радиусом r = a_y (см. рис. 3).

Продолжая решение задачи, находим скорость υ в момент времени t = 0 точечного соприкосновения шарообразного мелющего тела и сферической поверхности частицы (см. рис. 3), применяя для неупругого удара по допущению в) теорему о равенстве количества движения взаимодействующих тел до и после соударения [24, 28]:

m 0U0 =( m0 + m ) ик,

к

P υ0 m и =     =----и m„ + m      P , G ,  4п ■ Yr ■ R3

0                --1--1 +--Lc------- gg

где P = Ри - искомый внешний статический нагрузоч- ный параметр, тождественный силе измельчения P , когда и0 = 0 ; yc, V , G - соответственно плотность [26], объем [29] и вес стального шара-измельчителя (см. рис. 3),

Г кг А               , Н ус = 0,000007851      19,81 = 7,7■Ю-5 —-,

^ мм³ )              мм³

• 4   ,               4

V = -п R ³,G = у_с ■ V = — п■ y_c ■ R ³, 3 ^c 3 ^c

^   (13)

g = 9,81   = 9810    - ускорение силы тяжести.

с2с2

Для определения максимального сближения u_M = u _y ( t_M ) (см. рис. 3) воспользуемся известным оригинальным способом Рейли-Юнга [14, 30, 31], основанным на законе сохранения механической энергии [24, 28]

K + U = const ,                (14)

где K = K ( t ) - кинетическая составляющая выражения (14) от массы m ₀ + m ; U = U ( t ) - потенциальная энергия локальной деформации u_y = u _y ( t ) разрушаемой частицы (см. рис. 3).

В момент равновесия t = 0 компонента U ( 0 ) = 0, а скорость и ( 0 ) = ц, = max, и, следовательно, кинетическая энергия K ( 0 ) = K_mж . При t = t_M (см. рис. 4) система взаимодействующих шаров получает экстремальное перемещение u_M = u_y ( t_M ) = max и соответствующую потенциальную энергию u ( t_M ) = u_mж , когда и ( t_M ) = 0 и K ( t_M ) = 0 . Поэтому уравнение (14) можно записать в такой форме для этих двух граничных значений времени t = 0 и t = t_M :

Kmax + 0 = COnSt(15)

или

0 + Umax = COnSt , следовательно,

Umax = Kmax .(17)

Учитывая нелинейный характер функции (4) в зависимости от u [32], раскрываем равенство (17), используя (4) при P ^ Р и , (12), (13) и [14, 22, 29, 30]:

откуда uM и = f Р -du max        y     y

4 E  Г R • R Y

3 ( 1 - м 2 ) L R ч + R ^J

u M 3

j ^- y ² • du y =

4 E Г R • R ) 2 2    5

ч2

3 ( 1 - m ² ) ( R , + R ^J 5 ^M

K max

( m 0 + m ) ^U —

P и

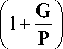
2 g

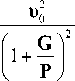
P и

2 g

Г.   4n • y • R ³I

1 +

I      3 P u    ^J

Из энергетического баланса (18) получаем

uM

15 Г 1 - M² I

16 1 E J

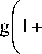
⁴ⁿ • Y c • ^R

3 P и

Г R ч + R Y I R ч • R J

— = — ( Р_и, R ) - физико-механический функциональ-

-                  Г Н • с21

ный коэффициент I      I,

I мм J

- 1 =

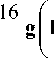
P и

4п • y _c • R ³ 1

3 Р и    J

— 2 = — 2 ( R , R ) — геометрическая характеристика моде

- 1

ли рис. 3, мм ,

— = R ^ ± R

² R ч • R

^R ч ^Г 1 ⁺ R Y

R ч • R

=-- 1--

R  R ч

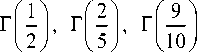
значения гамма-функций или

эллиптических интегралов второго рода [29, 33]:

Г | 1 | = ^П = 1,77245 ;

L 2 J

Имея в соответствии с (19) сближение u_M , находим согласно (4), (8) и зависимости [21]

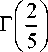
= 2,21815;

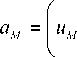
R • R

R + R J

( 9 )

Г — = 1,06863 .

UoJ искомые максимальные динамические параметры

(см. рис. 3):

Для определения статического усилия измельчения

Р_и используем прежде всего формулу (10), при t = 0 и и₀ = 0

4 K15

3 22

3 β5

2 K 1 ⁵

q 0 M       4

π β5

^и 0 ⁵ ,

1 - 2м

^: r = ° 1 =     ,   q 0 ,

где q - максимальное реактивное давление (см. рис. 3),

q ₀

для продолжительности контакта (см. рис. 4) [15, 22]

1 = — 3

π

6 P и

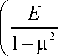
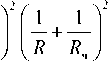
uM1   dξ t y    t-lM

υ ⁵

^{0 0} V1 - ^²

Г I ² Г I ¹ I 415Ц1 U m 5 Г Г 2)    U o

L 10 J

= 0,5784 Р_и³ и

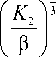
2 (К.

= 2,9432 -M- = 2,9432 ( в • — ) 5 1    2 I

^U 0                     L ^U 0 J

где в = в ( m, E ) — упругая константа материала

I мм2 ]

ц I Н J ^,

части-

в=¥;

от равнодействующей силы Ри [21,26], учитывая обозначения коэффициентов (24) и (26).

С целью математического описания предельного состояния измельчаемого шара применяем критерий прочности Галилея-Лейбница [21] в виде равенства [25-27]

° э = |°1| = ° вр ⁽³⁰⁾

с наибольшим по модулю эквивалентным статическим напряжением оэ, которое широко распространено в проектно-технических расчетах для весьма хрупких материалов, по-разному сопротивляющихся сжатию и

растяжению (о_вс >>  о_вр, см. предпосылку а) ). В справочно-нормативной литературе [26] формула (30) известна как гипотеза максимальных растягивающих [21] нормальных напряжений (первая теория прочности).

Подстановка выражений (28), (29) в условие несущей способности (30) приводит к алгебраическому уравнению относительно P ющего физико-механические константы [26, 27, 34]

о = 2,943 МПа I -Н | << с_вс = 255 МПа I Д- 1 , вр                                   2          вс                                2

V мм )                  V мм )

E = 48060 МПа |—г] , ц = 0,15 при скорости соуда-

V мм² )

рения υ , изменяющейся в пределах

1 - 2ц ° э =   3

1₃ 0,5784 Р и ³ I у I = % ,

⁰ <  ^и 0

< 1200 мм, с

радиусах поверхностей контакта

из решения которого

R = 20 мм >> R = 0...0,12 мм        (38)

р - f з Y в² • <  и (1 -2ц) 0,1935 К 2 ^.

Повторяя алгоритм (28)–(31), для ударного действия наибольшей инерционной силы Р_м = Р_у ( t_M ) (см. рис. 4), соответствующей статической нагрузке (32), будем иметь, учитывая (22), (24)–(26), главное функциональное соотношение решаемой задачи, представляющее собой критерий разрушения твердого хрупкого материала при его измельчении по гипотезе Галилея–Лейбница [25–27]:

_ 1 - 2ц     _1 - 2ц 2 К 5  3  5

' э М            q 0 M      ,      ■  4 ^К 2 • ^и 0

33π β5

вр

Для граничного случая

°эМ   °вр , аналогичного (30), находим в общем виде предельное значение скорости υ , меньше которой частица заданного радиуса R не будет измельчаться с учетом допущения д) [22]:

и удельном весе (13) мелющих шаров y_c = 7,7 ■Ю ⁵ ——т мм ³

(см. рис. 3). Уточняем также допущение з) условиями

R >  20 R , ^ 0 <  R <  0,05 R , ^ 0 <  К ₂<  1,05, (39)

ч           ч                      2    Rч учитывающими предполагаемые конструктивно-технологические особенности процесса помола.

Воспользовавшись приведенными количественными данными,

– вычисляем постоянную β в соответствии с (24):

1 - (0,15) 2                 мм²

в = —( ,  ) = 0,00002034----;(40)

48060Н

- находим зависимость Р_и = Р_и ( К ₂) , руководствуясь (32) и (40):

_ f 3 I3 (0,00002034)2 •(2,943)3 _ и = V1 - 2 • 0,15 )        0,1935 • K 2

0,00000429

, ^Н;

^K 2 ²

υ 0П

3п • %

2 ( 1 - 2ц )

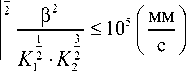
– определяем согласно (26), (38) значения функции

K₂ = K ₂ ( R ) , когда 0 <  R ₄ <  0,12 мм (табл. 1).

откуда после исключения

K на основании (25) и (32),

К₂ =1= 0,05 + .

²  20   R ч R ч

(2 fol ² и₀ = 0,4543 I I    -g-

^0п         1 2 ) ( K )

Таблица 1

Результаты расчета геометрического параметра K

Table 1

The results of calculation the geometric parameter K

R , мм	0	0,02	0,04	0,06	0,08	0,10	0,12
К 2, мм - 1	^	50,05	25,05	16,72	12,55	10,05	8,38

Далее, непосредственно проверяя соотношение (36) для каменных материалов с очень малыми величинами коэффициента в << 1 (см. результат (40)) и предел прочности σвр на растяжение, можно убедиться, что в подкоренном выражении (36) первое слагаемое всегда многократно – на несколько порядков меньше второго, т.е.

9в 2 ■ о 2р    4п ■ Y c ■ R ³ ( 1 - 2ц ) 0,1935 K 22

V ( 1 - 2ц ) 2⁺            9%

2        0,1935п ■ y c ■ R ( 1 - 2ц )

R ■ K 2                             ,

3                    σвр и на основании (43) формула (36) принимает упрощенный вид:

^U 0n = ^U 0n ( ^R ) =

= 72,32762 R

Y c ( 1 ^{- 2}И ) ^σ вр

R I       ММ

1 + — <  10⁵, — , (44)

R ч )      I с )

после подстановки физико-математических констант g = 9810 мм , п = 3,1416 и замены суммарной кривиз-с2

ны K контактирующих поверхностей (см. рис. 3)

в соответствии с (26) при выполнении условия 0 <  R <  0,05 R (см. (39)).

Потребовав соблюдения равенства и0П = U) = 105 мм,              (45)

с возможно количественно оценить тот минимально допустимый размер R*mn) частицы, при котором обеспечивается механико-математическая корректность и точность выведенных аналитических зависимостей (33), (44), содержащих физические постоянные E , μ , σвр . Заменяем предел прочности σ в общей формуле (33) и коэффициенты K , β для гранита, используя выражения (25), (40), (41). В итоге получаем два функциональных соотношения:

υ ²⁵

о э м = ° э м ( Uo , R ) = 0,779745 —0—,    (46)

K 2 ^{( R} 4 )

откуда при оэМ = о = 2,943 --- и R = 20 мм имеем р        мм2

и = иоп ( R ) = 27,67542VR = f i 112               f112

= 27,67542 - + —  = 27,67542 0,05 + —   , (47)

VR R ч)           I находим

—- =----⁰---- ₇ - 0,05, ^ R min ) = 7,66 -10 " ⁸ мм. (48)

R min)   (27,67542)2

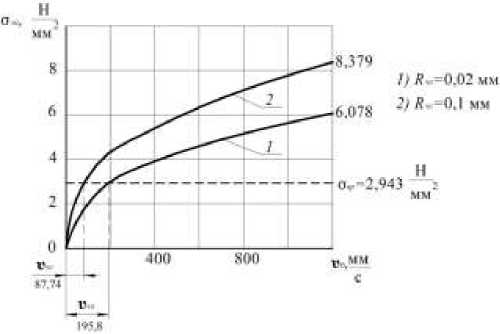
Графики функций о М = о М ( ^и о ) , о М = °_э М ( R ) , и₀ = и₀ ( R _п) , построенные по данным табл. 1, 2, 3, 4, изображены на рис. 5 и 6. Соответствующие расчеты проведены по представленным ниже формулам, в основе которых зависимости (46), (47):

• •    при R = 0,02 мм, ^ K = 50,05 мм ^{- 1} (см. табл. 1 и 2)

О эм = О эм ( и о ;0,02 ) = 0,35651 u 0’ ^{4 f} -Н ) ,

V мм )

< 0 <  и₀ <  1200 —,                         (49)

где и_Оп = 27,67545 ( 50,05 ) 0’5 = 195,8 — ; с

• •    при R = 0,1 мм, ^ K = 10,05 мм¹ (см. табл. 1 и 2)

О э М = О э М ( Uo ;0,1 ) = 0,4915 ■ u0’^{4 f} -Н ) ,

V мм )

< 0 <  и₀ <  1200 —,                         (50)

с где и0П = 27,67545 ■ (10,05)0’5 = 87,74 —;

с

• •    при и_Оп = 195,8^мм (см. табл. 1 и 3) с

  h       _А_ 6,43691 f Н I

^ОэМ   ^ОэМ ^{( 195,8; R} 4 )       „0,2 I      2 I ,

^K 2    ^{V мм )}

< 0 <  R ₄<  0,12 мм,                          (51)

где R _4D = 0,02 мм;

мм

• •    при и_Оп = 87,74 — (см. табл. 1 и 3) с

  -                4’66908 f Н I

ОэМ ОэМ (87,74; Rч)        0,2 I     2 I, к2’ Vмм )

0 <  R <  0,12 мм,

где ^_п = 0,1мм;

а из равенства (45) или

• при 0,002 мм <  ^ _п<  0,02 мм (см. табл. 4)

27,67542 0,05 +

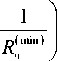
= 10⁵

f    W Н ип = 27,67545 0,05 +--- I —-

⁰                   R     | мм²

чп

.

Таблица 2

Таблица 3

Результаты вычислений функций (49), (50)

Table 2

The results of the calculations of the functions (49), (50)

мм υ 0, с	0	200	400	600	800	1000	1200
Н σэМ , мм2 R = 0,02 мм	0	2,968	3,916	4,606	5,168	5,65	6,078
Н σэМ , мм2 R = 0,1 мм	0	4,092	5,399	6,35	7,125	7,79	8,379

б

Рис. 5. Графическая иллюстрация функциональных формул (49)–(52): а – график зависимости эквивалентного напряжения σ от скорости υ ; б – график зависимости эквивалентного напряжения σ от радиуса частицы R

Fig. 5. Graphs of the functional formulae (49)–(52): a – graph of the dependence of the equivalent stress σ on the speed υ ;

b – graph of the dependence of the equivalent stress σ on the radius of the particle R

Численная информация о функциональных зависимостях (51), (52)

Table 3

The calculations of the functional dependences (51), (52)

R , мм	0	0,02	0,04	0,06	0,08	0,10	0,12
Н σ э , мм2 мм U 0n = 195,8--- с	0	2,943	3,38	3,665	3,881	4,057	4,208
Н σэ ,      2 мм2 мм U 0n = 87,74— с	0	2,135	2,452	2,658	2,815	2,943	3,052

Таблица 4

Расчетные данные к функции (53)

Table 4

Calculation data for the function (53)

R чп, мм	0,002	0,004	0,006	0,008	0,01	0,012	0,014	0,016	0,018	0,02
υ 0 , мм с	618,9	437,6	354,3	309,5	276,8	252,7	234	218,9	206,4	195,8

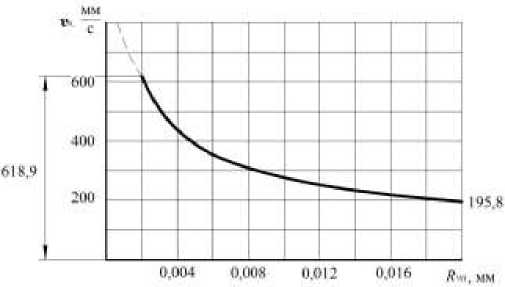
Рис. 6. Гиперболический график зависимости (53)

Fig.6. The hyperbolic graph of the dependence (53)

Завершая данную статью, дополняем аналитические соотношения (19)–(23), (32), (33), (44) полуэмпириче-скими формулами, аппроксимирующими с высокой точностью ударно-силовой импульс в промежутке времени 0 <  t <  t (см. рис. 4) [22]:

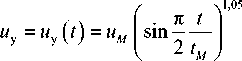
P y

1,635

= Py (t ) = PM I sin П T" I

V ² t M )

^u = ^u ( t ) = ^u 0 ■

1 -

2,725

■ П t 1

sin

.    2 t M )

где Um = uy (tM ), Pm = Py (tM ) , tM - Динамические ха рактеристики (19), (21), (23).

В то же время следует подчеркнуть, что параметры (54) и время t соударения (23) не имеют принципиального значения с практической точки зрения при изучении процесса помола материала. Однако необходимость их использования может возникнуть в случае уточненного математического моделирования разновидности удара, рассмотренной в этой статье (см. рис. 1 и 3), базируясь на фундаментальных положениях механики упругодеформируемого твердого тела [20] и колебательно-волновых теориях [14, 15, 21].

Комплексный анализ проведенных расчетно-теоретических исследований позволяет сделать следующие выводы:

u0 < 10 -- [22] получено оригинальное инженерно- с техническое решение динамической задачи теории упругости о контактном взаимодействии деформируемой неподвижной шаровой модели измельчаемого хрупкого материала с двумя абсолютно твердыми сфе- рическими телами, имеющими заданную массу и максимальную кинетическую энергию (см. рис. 1).

максимально допустимая величина  и(  ) = 10 -- с адекватна очень мелкому измельчению твердого вещества, когда порядок R™in^ оценивается 10-8 мм (48).