Обобщенная функция распределения срока службы приборов и агрегатов орбитальных станций

ДИДЕНКО А.Ф.

ПОМПУШКО А.З.

POMPUSHKO Alexander Zakharovich — Head of Sector at RSC Energia, Candidate of Science (Engineering)

Российские пилотируемые орбитальные станции (станция «Мир», Российский сегмент Международной космической станции (РС МКС) являются космическими объектами долговременной эксплуатации. В связи с длительным функционированием в космическом пространстве, сложностью и многочисленностью бортового оборудования для надежной и безопасной эксплуатации станций необходима оценка технического состояния их бортового оборудования по результатам летных испытаний, которая требуется для прогнозирования характеристик потоков отказов и обеспечения планового технического обслуживания космической станции. Одними из важнейших характеристик ee технического состояния являются показатели надежности.

Постановка задачи

При оценке показателей надежности российских орбитальных станций по результатам летных испытаний существует проблема представительной статистики, используемой для определения параметров функций распределения срока службы (долговечности эксплуатации) приборов и агрегатов (элементов) станции, а также проблема выбора функции распределения для вероятностного описания долговечности ее составных частей.

Данные проблемы связаны с тем, что за период эксплуатации используется относительно небольшое количество образцов элементов станции каждого типа, а также с тем, что длительность эксплуатации до отказа значительного количества элементов реально эксплуатируемых станций в несколько раз превышает установленные гарантийные показатели долговечности (ресурс и срок службы). Последнее приводит к тому, что использование в качестве закона распределения срока службы элементов станций экспоненциального распределения неприемлемо из-за существенного непостоянства (возрастания) интенсивностей отказов при длительных сроках эксплуатации.

Для преодоления перечисленных проблем разработана обобщенная функция распределения срока службы, единая для всей совокупности элементов станции, независимо от их функционального назначения и конструктивного исполнения. Предполагается, что это может обеспечить более высокую степень достоверности оценок показателей надежности станции вследствие того, что для определения параметров функции распределения может быть использована представительная выборка (порядка тысячи элементов).

Кроме того, в целях учета возрастания интенсивности отказов при большей продолжительности эксплуатации элементов структура данной функции распределения увязана с физической природой долговечности изделий.

В качестве элемента станции здесь рассматриваются законченный блок, прибор или агрегат, которые имеют самостоятельные гарантийные показатели долговечности.

Основанием для данного подхода является предположение о том, что, хотя элементы станции представляют собой широкую гамму конструкций, отличающихся физическими принципами функционирования, параметрами, разработчиками, условиями изготовления и т.п., их, в некотором смысле, можно рассматривать как выборку однородных объектов, так как все они созданы на единой нормативной базе по обеспечению надежности и сбалансированы по гарантийным срокам эксплуатации.

Математическая модель

Учет физической природы долговечности конструкции в обобщенной функции распределения срока службы элементов станции основан на следующих соотношениях.

Согласно работе [1] время функционирования изделий до отказа (разрушения) для большинства видов нагрузок подчиняется следующей типовой зависимости:

т Дг "". (1)

где τ — время работы конструкции до разрушения; σ — действующая удельная нагрузка; α, А ₀ — постоянные коэффициенты.

Под нагрузками здесь понимаются внешние воздействия любой физической природы, которым подвержена конструкция в ходе эксплуатации.

Фактическая удельная нагрузка, воздействующая на конструкцию, как правило, является величиной, переменной во времени. Однако поскольку при расчете долговечности применим принцип суперпозиции нагрузок, то далее будем рассматривать в качестве параметра σ некоторое среднеинтегральное значение нагрузки за время эксплуатации, обеспечивающее выполнение соотношения [1]:

г dt .

о ЭДО] ’ где t — текущее время эксплуатации; — долговечность конструкции при постоянной нагрузке, равной σ(t).

Далее при упоминании нагрузки термины «удельная» и «среднеинтегральное значение» для простоты изложения будут опускаться.

С целью получения обобщенной функции распределения срока службы, пригодной для различных видов конструкций и нагрузок, выражение (1) преобразуем следующим образом:

т = Лое "\

где а = ασ_пр; s = σ/σ_пр — безразмерная нагрузка, здесь σ_пр — предельная нагрузка.

В качестве предельной рассматривается нагрузка, при которой время работы конструкции до разрушения мало и не превосходит некоторого заданного значения.

Величина а является постоянным коэффициентом, а s — переменная, изменяющаяся в диапазоне 0…1.

Таким образом, выражение (2) дает зависимость для срока службы конструкции как функцию безразмерного отношения средней за время эксплуатации действующей нагрузки к предельной, что делает выражение (2) инвариантным по отношению к любым видам конструкций.

Для получения обобщенной вероятностной модели элементов станции приняты допущения:

• 1.    Так как начальная несущая способность конструкций достаточно жестко обеспечивается организацией производства и большим объемом испытаний, то случайные разбросы срока службы определяются, главным образом, случайной реализацией нагрузок, воздействующих на конструкцию при ее реальной эксплуатации.

• 2.    При правильном проектировании действующие нагрузки (в том числе и среднеинтегральные значения) на элементы станции имеют математические ожидания, соответствующие расчетным значениям, а ошибки определения нагрузок (разности между действующими и расчетными значениями) распределены по закону, близкому к нормальному, с нулевым математическим ожиданием и дисперсией, обеспечивающей достаточно малую вероятность достижения предельного (разрушающего) значения σ_пр.

Таким образом, если в качестве случайных величин рассматривать среднеинтегральные нагрузки, то согласно принятым допущениям закон распределения действующей безразмерной нагрузки s будет близок к нормальному с плотностью распределения:

1 ^2itDs

ехр[-

(s-Ms) 2Ds

где Ms — математическое ожидание безразмерной нагрузки; Ds — дисперсия безразмерной нагрузки.

Так как срок службы является функцией нагрузки (2), то плотность функции распределения величины τ( s ) можно определить через плотность распределения f_s [2]:

/-^(зУ'^^'у,(4)

где функция, обратная τ( s )

T(s) _ 5 _ « ^n Ло(5)

С учетом выражений (3) и (5) уравнение (4) может быть записано в следующем виде:

^^ри^^"^''(6)

где x =In——.

Выражение (6) принято в качестве плотности обобщенной функции распределения долговечности элементов станции. Типовые характеристики данной функции распределения показаны на рис. 1.

F(t),f(t)

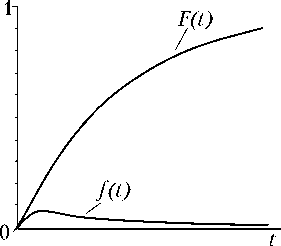
Рис. 1. Типовой вид графиков обобщенной функции распределения F(t) и плотности распределения f(t) долговечности элементов орбитальных станций

Значения параметров Ms, Ds, а и А ₀ подлежат определению по результатам обработки статистики отказов элементов станции в целом.

Экспериментальная проверка

Адекватность предложенной обобщенной функции распределения проверена путем моделирования потоков отказов орбитальной станции «Мир», а также потоков отказов модулей РС МКС с использованием данной функции и последующим сравнением результатов моделирования и фактических потоков отказов.

Для определения параметров обобщенной функции распределения и подтверждения адекватности предлагаемого вида функции распределения реальным характеристикам надежности элементов модулей орбитальных станций была разработана компьютерная про- грамма для моделирования потоков отказов модулей станции.

Алгоритм, реализуемый программой, состоит в численном статистическом моделировании потоков отказов модулей станции. Для формирования потока отказов используется обобщенная функция распределения долговечности элементов станции (6). Модули станции рассматриваются как сложные восстанавливаемые технические системы. Восстановление после отказа элемента (ремонт) производится путем замены отказавшего элемента на исправный или каким-либо иным способом. При моделировании принято, что после ремонта восстановленный элемент имеет исходную функцию распределения времени функционирования до отказа. В модели учитывается количество элементов, из которых состоит каждый модуль.

Значения параметров функции распределения при использовании данного алгоритма находятся таким образом, чтобы обеспечить максимальную близость между расчетными характеристиками потоков отказов и статистическими данными о потоках отказов реальных модулей.

Оценки параметров обобщенных функций распределения с использованием упомянутого алгоритма получены для двух типов отказов:

• •    для отказов, потребовавших замены материальной части на новую;

• •    для несоответствий — всех видов отказов, включая незначительные, самоустранившиеся или устраненные мелким ремонтом.

Предполагается, что основным отличием второго типа отказов от первого является то, что при проектировании изделий и выборе расчетных случаев, для оценки их несущей способности, возможным незначительным отказам, по понятным причинам, уделяется меньше внимания, чем возможным отказам, имеющим серьезные последствия, из-за чего функция распределения для отказов второго типа должна отличаться большими значениями математического ожидания безразмерной нагрузки Ms и дисперсии Ds .

Оценка параметров обобщенных функций распределения по исходным данным (статистике отказов) орбитальной станции «Мир» с 1986 по 1992 годы дала следующие результаты:

• •    для отказов первого типа: а = 8,63; А ₀ = 700; Ms = 0,49; Ds = 0,017;

• •    для несоответствий: а = 8,63; А ₀ = 700; Ms = 0,52; Ds = 0,073.

Степень совпадения результатов расчетов по математической модели с фактическими потоками отказов обоих типов для различных модулей станции «Мир» с 1986 по 1999 годы, а также РС МКС с 1998 по 2011 годы, отличающихся числом элементов и датами запуска, демонстрируется графиками, приведенными на рис. 2–7.

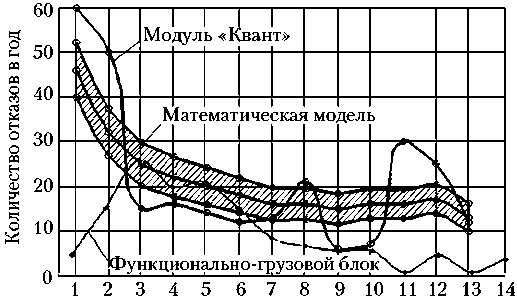
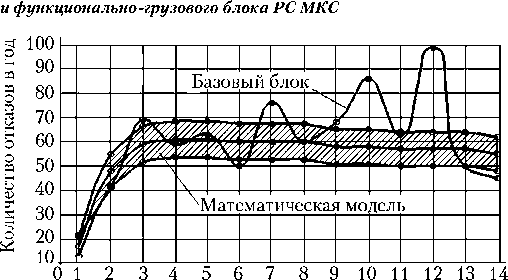
Заштрихованными областями показаны результаты моделирования, а именно: математические ожидания (средняя линия заштрихованной области) плюс/минус среднеквадратичные отклонения (граничные линии заштрихованной области) оценок количества отказов в год по годам эксплуатации модулей станций. Фактические значения количества отказов в соответствующие годы эксплуатации модулей станций отмечены точками, соединенными сплошными линиями.

Как видно из графиков на рис. 2–7, специфические особенности поведения моделируемых потоков отказов различных типов, а также абсолютные значения количества отказов для различных модулей согласуются с особенностями поведения соответствующих фактических потоков отказов модулей станций. Подтверждаются также ожидаемые отличия в значениях параметров обобщенных функций распределения для отказов различных типов.

Это свидетельствует о том, что вид обобщенной функции распределения, использованной при моделировании, адекватно описывает реальные вероятностные характеристики долговечности эксплуатации элементов станции. Отдельные имеющие место значительные отклонения фактических значений количества отказов модулей от расчетных значений следует объяснить тем, что реальный процесс проявления отказов и восстановления работоспособности станции является случайным и обусловлен не только вероятностной природой долговечности элементов, но и методами восстановления работоспособности и спецификой организации эксплуатации станции.

Соответствие теоретических результатов и экспериментальных данных проверено путем оценки согласия между эмпирическими функциями распределения отклонений потоков отказов от теоретических математических ожиданий и нормальным законом распределения. Значения критерия согласия Колмогорова А _К составили для потоков отказов первого типа — А _К = 0,14, для потоков несоответствий — А _К = 0,253 при числе степеней свободы n = 31, что свидетельствует об удовлетворительном соответствии между теоретическими результатами и экспериментальными данными.

Базовый блок

Математическая модель

' Служебный модуль

^   0 1 2 3 4 5 6 7 8 9 10 И 12 13 14

Продолжительность эксплуатации, годы

Рис. 2. Результаты математического моделирования и реальные потоки несоответствий базового блока станции «Мир» и служебного модуля РС МКС

Продолжительность эксплуатации, годы

Рис. 3. Результаты математического моделирования и реальные потоки несоответствий модуля «Квант» станции «Мир»

Продолжительность эксплуатации, годы

Рис. 4. Результаты математического моделирования и реальные потоки отказов, потребовавших замены матчасти на новую, базового блока станции «Мир»

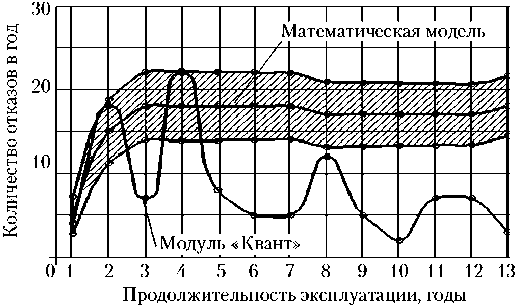
Рис. 5. Результаты математического моделирования и реальные потоки отказов, потребовавших замены матчасти на новую, модуля «Квант» станции «Мир»

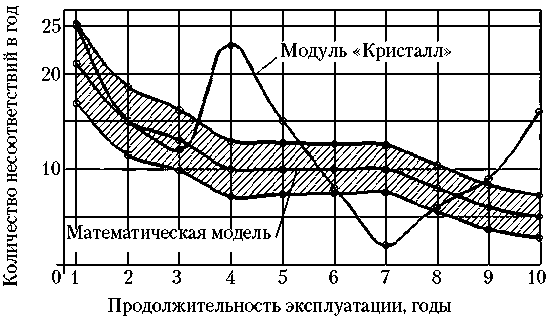
Рис. 6. Результаты математического моделирования и реальные потоки несоответствий модуля «Кристалл» станции «Мир»

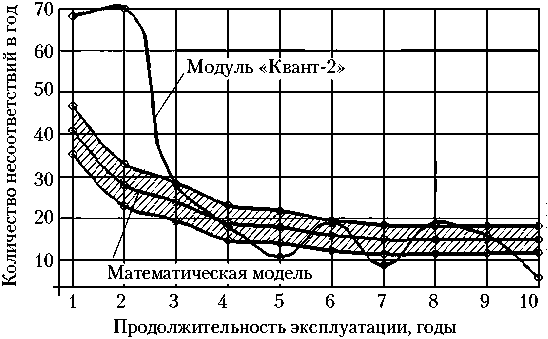
Рис. 7. Результаты математического моделирования и реальные потоки несоответствий модуля «Квант-2» станции «Мир»

Выводы

Разработана обобщенная функция распределения срока службы элементов российских орбитальных станций, которая учитывает особенности физической природы возникновения отказов.

Разработанная обобщенная функция распределения описывает вероятностные характеристики долговечности эксплуатации элементов российских орбитальных станций.

Математическая модель процесса восстановления, основанная на использовании этой функции, может применяться для оценки показателей надежности, а также для прогнозирования параметров потоков отказов при проектировании и эксплуатации модулей станций.