Обобщенная кинетика радиационных процессов в поле ультракоротких импульсов: физико-математическая модель
Автор: Астапенко В.А., Кротов Ю.А., Храмов Е.С.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Физика
Статья в выпуске: 4 (56) т.14, 2022 года.
Бесплатный доступ
Предложена физико-математическая модель обобщенной кинетики радиационных процессов в поле ультракоротких импульсов, базирующаяся на использовании вероятности фотопроцесса в заданный момент времени вместо стандартного подхода, который использует постоянную во времени скорость фотоиндуцированного перехода. Получены основные выражения для населенности верхнего энергетического уровня двухуровневой системы, возбуждаемой импульсом с экспоненциальной огибающей. Показано существенное отличие предложенной модели от результатов стандартного подхода в случае ультракоротких импульсов с длительностью, меньшей времени фазовой релаксации двухуровневой системы.
Кинетика фотопроцесса, ультракороткий импульс, вероятность фотовозбуждения, двухуровневая система
Короткий адрес: https://sciup.org/142236482
IDR: 142236482 | УДК: 535.3
Текст научной статьи Обобщенная кинетика радиационных процессов в поле ультракоротких импульсов: физико-математическая модель
Достигнутые в последние десятилетия успехи в методах генерации лазерных импульсов различной длительности, включая ультракороткие (УКИ) [1], делают актуальным развитие адекватных, универсальных и, по возможности, простых способов описания взаимодействия таких импульсов с веществом. Стандартный метод базируется на. использовании вероятности фотопроцесса. в единицу времени или сечения [2]. Такой подход не учитывает,
однако, специфики ультрабыстрого электромагнитного взаимодействия, при котором параметры лазерного импульса непосредственно «встраиваются» в элементарный излучательный акт. Поэтому невозможно на формульном уровне разделить вероятность на простое произведение полевой и «вещественной» частей.
В ряде работ одного из авторов этой статьи было предложен «вероятностный» подход к описанию фотопроцессов в поле УКИ, в котором основную роль играет безразмерная вероятность процесса либо за все время действия импульса [3], либо в заданный момент времени [4].
С целью распространения этого подхода на широкий круг радиационных явлений, индуцированных УКИ, представляется важным построить обобщенную кинетику фотопроцессов, базирующуюся на вероятности в заданный момент времени. Данная статья посвящена развитию физико-математической модели обобщенной кинетики на простейшем примере фотовозбуждения двухуровневой системы под действием УКИ.
2. Кинетика населенностей двухуровневой системы
Кинетика населенностей двухуровневой системы (ДУС) в поле теплового излучения была впервые рассмотрена А. Эйнштейном в фундаментальной работе [5]. В этой статье было выведено уравнение баланса для населенностей двухуровневой квантовой системы (V1,2) в предположении, что переходы между уровнями происходят в результате поглощения и испускания теплового фотона, а также вследствие спонтанного излучения.
В дальнейшем кинетическое уравнение Эйнштейна было адаптировано для описания взаимодействия лазерного излучения с дипольно-разрешенным переходом в двухуровневой системе (см., например, [6]):
V +
V - Ne
Т1
— 2 w , V.
здесь V2 — V1 - инверсия населенностей в заданный момент времени, Ve - равновесная инверсия населенностей (без резонансного излучения), Т1 - время релаксации населенности (продольное время релаксации), Wj = const - скорость переходов между уровнями под действием излучения (вероятность в единицу времени).
В рассматриваемом приближении двухуровневой системы условие нормировки имеет вид
V1 + V2 = 1.
Кинетическое уравнение для населенности верхнего уровня ДУС в предположении Ve = 0 может с учетом равенства (2) записано следующим образом:
dV2V
— + т = Wj [1 — 2V].(3)
Стандартный кинетический подход отвечает условию Wj = const. Тогда решение уравнения (3) дается равенством:
V ?"■“ (t) = Ө(t) 'Д [1 — exp (— 1 — 2ШІТ1) 1 ,
1 + 2wj Ті [ \ Ті/ j где Ө(t) - ступенчатая функция Хэвисайда. При записи (4) было учтено, что резонансное излучение включается в нулевой момент времени. В пределе больших времен t >> Ті из (4) имеем
V; — :! ^ ^) = Ө(t) WТА = (W.Ті >> 1) = 1.
1 + 2wj Т1 2
Второе равенство в этой формуле соответствует эффекту насыщения.
Выражение для скорости/вероятности в единицу времени радиационного процесса имеет вид [7]:
Wi — 2 С(Шс)Ио,
здесь Ио - резонансная частота Раби, пропорциональная амплитуде напряженности электрического поля в импульсе, G(w) - спектральная форма линии радиационного перехода в ДУС, шс - несущая частота возбуждающего импульса.
Рассматриваемое в данной статье обобщение кинетики заключается в предположении, что скорость радиационного перехода не является константой, а зависит от времени:
Wj ^ w(t).
С учетом (7) уравнение (3) перепишется в виде
/у + У — w(t)[1 - 2V,]. (За)
Введем безразмерную вероятность фотоиндуцированного перехода в заданный момент времени по формуле:
W (t) — J w(t' ) dt' .
Тогда решение уравнения (За) можно записать в следующем виде:
V2 2W (t) 1. Сexp [ д + 2W(t‘)] dt'^ . В пренебрежении релаксацией верхнего энергетического уровня ДУС (Д ^ то) формула (9) упрощается к виду N2(t,Ti ^ то) — 2 {1 - exp [-2 W(t)]} . (9а) Отметим, что в пределе теории возмущений из (9а) следует, что N2(t) — W(t). В рамках первого порядка теории возмущений для вероятности возбуждения квантовой системы в заданный момент времени в статье [4] было получено выражение через сечение фотовозбуждения, которое для ДУС может быть переписано через резонансную частоту Раби: Wexc(t) — ШоИ2 [ ^^-Dt w)dw, о ш D(t,w) — [ -∞ ′ E(t')eM dt' , E(t) E(t). Ео (И) где Ео - амплитуда электрического поля в импульсе E(t), шо - собственная частота ДУС. Существенное предположение рассматриваемой модели заключается в равенстве вероятностей (8) и (10).
3. Фотовозбуждение под действием экспоненциального импульса В дальнейшем рассмотрим возбуждающий электромагнитный импульс с экспоненциальной огибающей: Еер (t) — Ө(t)Eо exp - -1) cos(шct), где т - длительность импульса. Отметим, что импульс (12) применяется, в частности, для описания лазерного импульса в режиме модуляции добротности. Кроме того, экспоненциальная огибающая позволяет провести рассмотрение в аналитическом виде. Так, в приближении вращающейся волны для функции D(t, ш) получается следующее выражение: - , х 1 > 1 + exp (——) — 2 exp (— -) cos [(ш — шс)] D ЕР (1,т,ш) = -Ө(^т2-----И.(13) 4 1 + т2 (ш — шс) В монохроматическом пределе т >> Т2 формулы (10) и (13) дают: Wep(t) « |С(шс)^0т (1 — е-■) .(14) Отсюда для времен t << т получаем Wep(t << т, т >> Т2) « ^(ДшДП^ = Wit.(15) To есть безразмерная вероятность возбуждения линейно возрастает со временем и верно соотношение: Wep ^t (t << т, т >> Т2) = wi = const.(16) В общем же случае, как это следует, в частности, из выражения (14) ^^ = const. В этом состоит существенное отличие обобщенной кинетики от стандартного подхода. Подставляя выражение (13) в формулы (10) и (9), получаем временную зависимость населенностей верхнего энергетического уровня ДУС в рамках обобщенной кинетической модели, которую можно проанализировать для различных параметров УКИ.
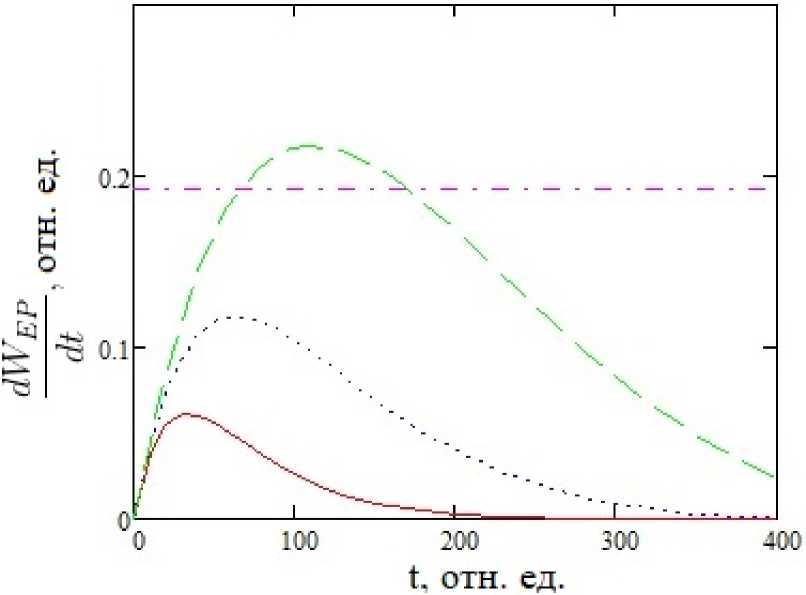
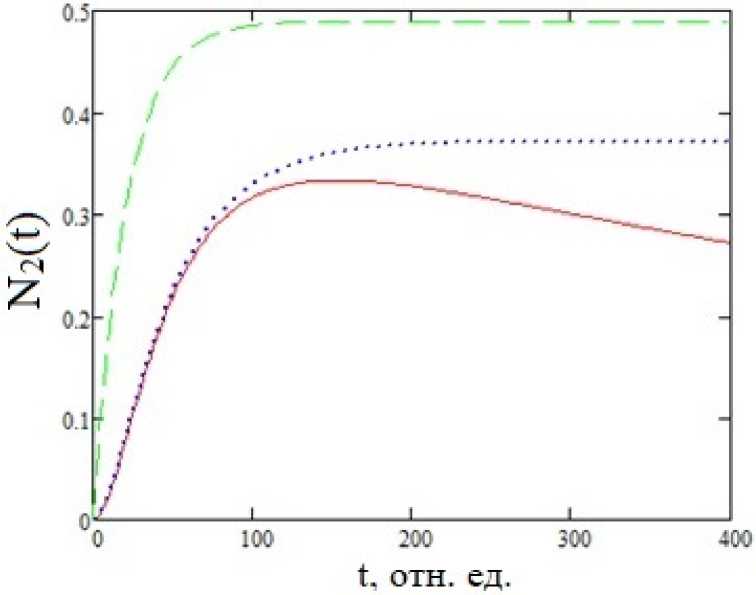
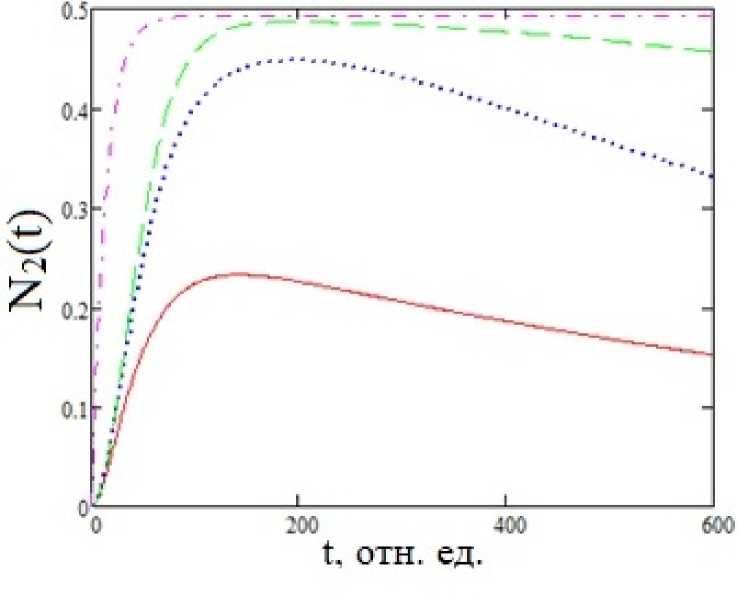
4. Результаты и обсуждение Результаты расчетов по вышеприведенным формулам представлены на рис. 1-4 для собственной частоты ДУС шо = 0.375 отн. ед. Значения всех параметров задачи приведены в относительных единицах. Это возможно, поскольку используемые расчетные выражения инвариантны относительно следующего масштабного преобразования: временные параметры ^ временные параметрыхК. частотные параметры ^ (частотные параметры) К. где К - произвольный масштабный множитель размерности частоты (положительное действительное число). На рис. 1 представлена временная зависимость скорости фотоиндуцированного процесса от времени для экспоненциального импульса в рамках рассматриваемого и стандартного подходов для случая длинных импульсов т >> Т2. Видно, что с ростом длительности импульса и для больших времен зависимость вероятности в единицу времени стремится к константе, определяемой формулой (6). В случае коротких импульсов т << Т2 имеем качественно другую картину, представленную на рис. 2. Скорость фотовозбуждения на временах t > т стремится к нулю, что естественно, поскольку импульс закончился. При этом функция ^ имеет максимум, смещающийся в область больших времен с ростом длительности импульса. Сравнение расчетов временной зависимости населенности верхнего уровня ДУС, полученных в рамках различных подходов, приведено на рис. 3 для случая короткого импульса т << Т1 ,Т2. Использовались три формулы: (4) - стандартный подход, (9) - обобщенная кинетика с учетом времени релаксации населенности и (9а) - обобщенная кинетика без учета Т1. Видно существенное отличие результата обобщенной кинетики от стандартного подхода, а также заметное влияние учета конечности параметра Т1 для больших времен. Рис. 1. Скорость радиационного перехода, как функция времени для случая длинных экспоненциальных импульсов различной длительности: сплошная кривая - т = 103, пуиктир - = = 5 • 103, штриховая кривая - т = 104; штрихиуиктир - Wi = con st, Т2 = 50, wc = 0.37, Ио = 0.1 Рис. 2. Скорость радиационного перехода, как функция времени для случая коротких экспоненциальных импульсов различной длительности: сплошная кривая - т = 50, пуиктир = т = 100, штриховая кривая - т = 200; штрихи уиктир - Wj = con st, Т2 = 103, шс = 0.37, Ио = 0.1 Рис. 3. Временная зависимость населенности верхнего уровня ДУС под действием экспоненциального импульса: сплошная кривая - обобщенная кинетика с учетом Т1, пунктир - обобщенная кинетика без учета Т1, штриховая кривая - стандартный подход; т = 50, Т2 = 103, Т1 = 103, шс = 0.37, И0 = 0.035 Рис. 4. Временная зависимость населенности верхнего уровня ДУС под действием экспоненциальных импульсов различной длительности: сплошная кривая - т = 50, пунктир - т = 150, штриховая кривая - т = 500, штрихпуиктир - стандартный подход Т2 = 102, Т1 = 103, шс = 0.37, По = 0.03 Рассчитанные в рамках обобщенной кинетической модели временные зависимости населенности верхнего энергетического уровня ДУС, возбуждаемой экспоненциальными импульсами различной длительности, представлены на рис. 4. На этом же рисунке для сравнения приведен результат стандартного подхода. Как и следовало ожидать, с ростом длительности импульса временная зависимость -У2(і) приближается к результату стандартного подхода, возрастая по величине.
5. Заключение На примере возбуждения ДУС под действием УКИ предложена физикоматематическая модель кинетики населенностей в терминах вероятности фотоиндуциро-ванного перехода, зависящей от времени, для которой использовалось ранее полученное выражение. Выведены формулы для населенности ДУС с учетом релаксации верхнего уровня. Рассмотрены различные предельные случаи полученных выражений. Проведены расчеты временной зависимости населенности ДУС, возбуждаемой импульсами с экспоненциальной огибающей для различных значений параметров задачи. Показано, что в пределе длинных импульсов результат обобщенной кинетической модели приближается к результату стандартного подхода. В случае коротких импульсов (с длительностью, меньшей времени фазовой релаксации) предложенная модель дает существенно иной результат. Работа выполнена при финансовой поддержке Российского научного фонда (Соглашение № 22-22-00537).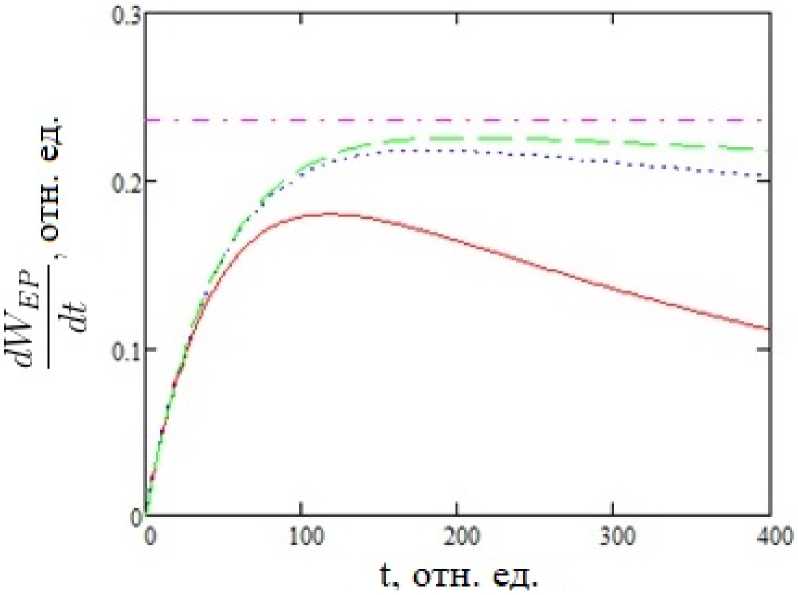
Список литературы Обобщенная кинетика радиационных процессов в поле ультракоротких импульсов: физико-математическая модель
- Ландау Л.М., Лифшиц Е.М. Квантовая механика. Москва: Наука, 1974.
- Chini M., Zhao K., Chang Z. The generation, characterization and applications of broadband isolated attosecond pulses // Nature Photonics. 2014. V. 8, N 3. P. 178-186.
- Astapenko V.A. Simple formula for photoprocesses in the ultrashort electromagnetic field // Physics Letters A. 2010. V. 374. P. 315-327.
- Астапенко В.А. Аттосекундная динамика фотовозбуждения атома водорода ультра-короткими лазерными импульсами // ЖЭТФ. 2020. Т. 157, вып. 1. С. 67-73.
- Einstein A. Strahlungs-Emission und - Absorption nach der Quantentheorie // Verhandl. Dtsch. Phys. Ges. 1916. V. 18. P. 318-323.
- Астапенко В.А. Взаимодействие излучения с атомами и наночастицами. Долгопрудный: Издательский дом "Интеллект", 2010. 496 с.
- Астапенко В.А., Сахно С.В. Некогерентный предел уравнений Блоха: переход к балансному уравнению и скорости фотоиндуцированного процесса // Труды МФТИ. 2022. Т. 14, вып. 2. С. 189-194.


