Обобщенная вероятностная модель оценки геодинамической устойчивости среды территориальных природно-технических систем

Вероятностные1 модели оценки геодинами-ческого2 риска, как показано в работах [1–3], в последнее время3 приобретают все4 большую теоретическую и практическую значимость. Подобные модели наглядно демонстрируют вероятность геодинамического риска не для какой-либо территории (региона, распределенной природнотехнической системы – РПТС) в целом, а характеризуют «точечно-площадную» вероятность такого риска, т.е. риска для территорий и объектов относительно малой протяженности. Рассмотрим особенности построения вероятностной модели оценки геодинамической устойчивости среды РПТС.

Вероятностная модель оценки геодинами-ческой устойчивости среды

Предположим, что последовательность гео-динамических состояний среды некоторой достаточно протяженной РПТС представляет собой поток однородных событий, который удовлетворяет условиям независимости, однородности и ординарности, т.е. представляет собой так называемый простейший поток.

Действительно, учитывая геологический генезис геодинамических рисков, возникающих в среде РПТС, в первом приближении мы можем допустить, что число проявлений опасных гео-динамических процессов в каждом из двух произвольно взятых, одинаковых по длительности и следующих друг за другом временных интервалов [a, b] и [c, d] не зависят друг от друга [1]. Из той же геологической природы рассматриваемых нами геодинамических рисков следует, что вероятность реализации подобных опасностей в течение временного интервала [a, b] совпадает с вероятностью реализации этих опасностей в течение временного интервала [c, d], что фактически означает соблюдение условия однородности. Если же за один и тот же бесконечно малый промежуток времени реализуются две геодина-мические опасности, то в геофизическом смысле энергетически они рассматриваются как одно событие, т.е. выполняется и условие ординарности.

Обозначая через P k ( t ) вероятность того, что в течение некоторого промежутка времени длительности t к процессу реализации различных геодинамических состояний среды РПТС будут предъявлены к требований (различных геодина-мических процессов), а также учитывая, что эта вероятность не зависит ни от выбора системы отсчета, ни от предыстории РПТС, мы можем однозначно построить формулы для определения вероятностей P k ( t ) [2-3].

Для построения таких формул в работах [13] определяются так называемые геодинамиче-ские состояния среды РПТС.

Предположим, что в некоторый момент времени t ₀ геосреда РПТС обладает некоторым энергетическим параметром геодинамических процессов (ГП) E ₀, количественно характеризующим их энергию.

Тогда состоянием 1 назовем такое состояние геосреды РПТС, при котором A E 1 = E 1 - E ₀ ^ 0, т.е. геосреда РПТС находится в равновесном устойчивом состоянии ( E ₁ - энергетический параметр ГП в среде РПТС в момент времени t ₁).

Состоянием 2 назовем состояние геосреды РПТС, при котором среда находится в неустойчивом неравновесном состоянии, т.е. A E ₂ = E ₂ - E 1 Ф 0 ( E ₂ - энергетический параметр ГП в среде РПТС в момент времени t ₂).

И состоянием 3 назовем квазиравновес-ное состояние геосреды РПТС, при котором A E ₃ = E ₃ - E 1 Ф 0, причем A E 1 < A E ₃<< A E ₂ ( E ₃ - энергетический параметр ГП в среде РПТС в момент времени t ₃).

Указанные состояния и переходы среды РПТС между ними графически представлены на рис. 1.

Величины a ij (где i = 1, 2, 3; j = 1, 2, 3) физически отражают суммарное воздействие энергетических параметров процессов, окончание которых приводит к непосредственному переходу геосреды из состояния i в состояние j (рис. 1).

В таком случае изменения вероятностей p 1 ( t ), p ₂( t ), p ₃( t ) нахождения среды РПТС в состояниях 1, 2, 3, с учетом всего вышеизложен-

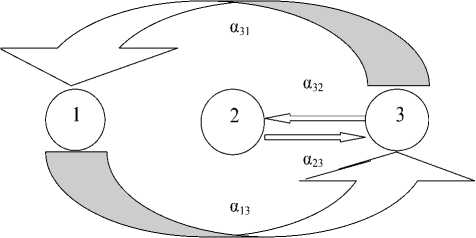
Рис. 1. Схема взаимопереходов геологической среды РПТС между состояниями 1, 2, 3

ного, будут описываться следующей системой дифференциальных уравнений Колмогорова:

p ‘ ⁽ t ) =-а_и p/ t ) + « 3, p 3⁽ t X

< p 2 ⁽ t ) = ^- « 23 p 2⁽ t ) ⁺ « 32 p 3⁽ t X                   ⁽¹⁾

_ p 3 ⁽ t ) = a_X 3 p_} ⁽ t ) + « 23 p 2 ⁽ t ) ^{- (}« 3i ⁺ « 32 ) p 3 ⁽ t )• Матрица коэффициентов системы (1) V a j является вырожденной, поэтому для ее разрешения любое из ее уравнений (например, третье) заменим условием нормировки, т.е. условием p_x ( t ) + p ₂ ( t ) + p ₃( t ) = 1. Тогда система уравнений (1) перепишется в виде:

'- « в p , ( t ) + а 3, p 3 ( t ) = p ‘( t ), ‘ ^{- а} 23 p 2⁽ t ) ^{+ a} 32 p 3⁽ t ) = p ‘ ⁽ t X . p ,⁽ t ) + p ₂ ⁽ t ) + p 3⁽ t ) = 1.

Поскольку геодинамические процессы протекают в среде РПТС в течение достаточно длительного времени, то имеет смысл говорить о предельном поведении вероятностей p i ( t ) при t ^^ [2].

Предполагая для среды РПТС существование предельных (финальных) вероятностей состояний 1, 2, 3, т.е. существование вероятностей p i = lim p i ( t ), не зависящих от того, в каком состоянии среда находилась в условный начальный момент времени, мы можем также предположить установление в среде РПТС предельного стационарного режима, при котором она переходит из состояния в состояние, но вероятности состояний p_i уже не меняются во времени.

В таком случае финальные вероятности состояния среды РПТС находятся из решения системы линейных алгебраических уравнений, получаемых из дифференциальных уравнений Колмогорова. Для этой цели необходимо приравнять производные вероятностей к нулю, а вероятностные функции состояний p i ( t ) в правых частях уравнений Колмогорова заменить на неизвестные финальные вероятности p i [2]:

ВЕСТНИК 2013 № 4

'- « 13 Р 1 + « 31 P 3 = 0,

< -a₂₃p 2 + a₃₂p₃ = 0,                          (3)

p i =

^a i3 ^a 23

^a 23 ^a 31

^{+ a} _B ^a 32 + ^a 23 ^a 3i

. P i + p 2 + p 3 = 1.

Определитель матрицы коэффициентов системы (3) отличен от нуля ^ a j , поэтому система уравнений (3) имеет единственное решение, а именно:

ВЕСТНИК 2013 № 4

p 3 = ^{1 -} p i ^- p 2 .

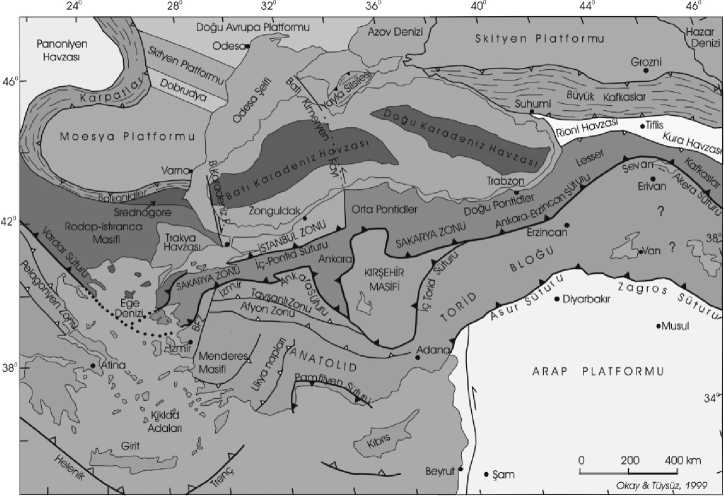
Рис. 2. Тектоническая карта территории Турции и прилегающих к ней государств

По рассчитанным таким образом вероятностям нахождения среды в работах [1–5] были построены оценочно-прогностические карты эквипотенциального распределения показателя комплексного риска ЧС геодинамического характера для различных РПТС.

Существенным недостатком подобной модели, на наш взгляд, является то, что она не учитывает в явном виде геологических неоднородностей среды РПТС (например, см. рис. 2 применительно к территории Турции).

Между тем, учет влияния таких неоднородностей, как тектонические разломные нарушения, является очень существенным при оценке геодинамической устойчивости среды РПТС, так как не всегда аномалии гравитационного поля соответствуют существованию тектонических разломных нарушений.

Предположим, что вдоль таких тектонических разломных нарушений идет процесс переноса сейсмодеформационной энергии как после произошедшего сейсмического события, так и в период его подготовки. Тогда особую значимость при этом будет иметь учет мест пересе-

^a _n ^{+ a} 1

p 2 = 1 - -13----- pi, a3i

чений тектонических разломов, так называемых тектонических узлов.

То есть, для того чтобы более точно оценить геодинамическую устойчивость среды РПТС, необходимо уметь определять величину сейсмической энергии, запасенную в каком-либо объеме геосреды, величину выделившейся при сейсмическом событии энергии и величину этой энергии, переданную по системе тектонических разломов. Узлы при этом играют роль специфических «клапанных механизмов», сдерживающих или пропускающих сейсмическую энергию в том или ином направлении.

Рассмотрим в этих предположениях обобщенную вероятностную модель оценки геодина-мической устойчивости среды распределенных природно-технических систем.

Обобщенная вероятностная модель

Представим упрощенно, в первом приближении, некоторую территорию (участок РПТС) в виде системы четырех узлов и соединяющих их друг с другом тектонических разломных нарушений геосреды (рис. 3). (Собственно говоря,

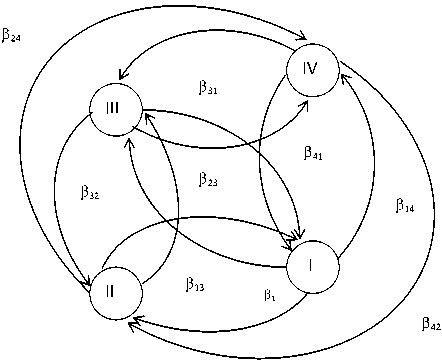
Рис. 3. Разломно-узловая тектоническая модель участка территории распределенной природно-технической системы

количество узлов может быть и значительно большим. С практической точки зрения их количество обусловлено следующими факторами. В первую очередь, число узлов зависит от тектонической неоднородности территории. Для локальных РПТС это то же самое, что и участки с повышенной трещиноватостью геологической среды. Во-вторых, важно учитывать таксонометрическую градацию территории, т.е. на каком иерархическом уровне мы выделяем отдельные блоки общей структуры геосреды РПТС. И, наконец, надо принимать во внимание общую протяженность исследуемой территории. Мы же в настоящей статье именно для упрощения описания нашего метода отвлеченно берем участок некоторой «абстрактной» территории с четырьмя узлами и соединяющими их тектоническими разломами.)

Согласно нашим модельным построениям, на первом этапе необходимо оценить вероятность события А – «передачи» сейсмодеформацион-ной энергии из узла I. Эта схема уже известна и стандартна для переходов по энергетическим состояниям 1, 2, 3, на что мы уже указывали ранее в предыдущем разделе. Передача сейсмоде-формационной энергии произойдет только в том случае, если будет реализовано сейсмическое событие определенного энергетического класса с вероятностью p 2 , т.е. P(A ) = p 2 .

Тогда, учитывая соотношения (2) и (3), мы можем достаточно легко найти выражение для определения вероятности события A :

P ( A ) =-------- ^ -- (5)

^а 32 ^а 13 + ^a 23^{( a} 31 + ^а 13 )

На этом этапе необходима оценка коэффициентов интенсивности процессов aij. Эти коэф- фициенты должны быть пронормированы, а их величины определяются на основании комплексной оценки следующих величин:

^а 13 = E p ; « 31 = E p ^- D E p ;

S E ,

'з2 = Ер + 1^г + up; Оз = Ер + uir + up —

р       r      z ^э        р       r      z

а где D

E p

– величина рассеяния потенциальной энергии Ep деформируемых пород геосреды;

–

S_E – величина сброшенной энергии при земле- 2ци_г ²      .    2ци₂ ²

трясениях; ur. = —r^- , иz = —- соответ-

•

•

ственно, обобщенные (переведенные в энергетические единицы) значения горизонтальных u_r и вертикальных u _z смещений в геологической среде.

Для оценки величины D_{E p} необходимо знать значения модуля сдвига μ и вязкости среды η для конкретного рассматриваемого объема этой геосреды. Для оценки величины S_E необходима информация о произошедших сейсмических событиях в пределах данного объема геосреды (магнитуды, глубины залегания очага).

На втором этапе выполняется оценка вероятности события B – возможности «передачи» сейсмодеформационной энергии из области I в смежные с ней области, например в области II, III, IV.

Итак, допустим, что для каждой из указанных областей известны вероятности «передачи» энергии, рассчитываемые по формулам вида:

P ^{( k} )( A ) = — а где к = 1, .„,4.

« 1133 ) & 32 )

ВЕСТНИК 2013 № 4

г 3 ^ ) + a 2 k ) ( a 3 k ) + а₃ ) )’

Тогда взаимодействия для данных областей будут описываться следующей системой уравнений:

<

Р 1' ( t ) = ^ 31 Р 3 ( t ) + в 21 Р 2 ( t ) + в 41 Р 4 ( t ) - ( в + в 12 + в м) Р 1 ( t ), Р 2 ( t ) = Д 2 Р , ( t ) + в Р 3 ( t ) + в 42 Р 4 ( t ) - в + в + в 4 ) Р 2 ( t ), Р 3 ( t ) = в 13 Р 1 ( t ) + в23 Р 2 ( t ) + Р43 Р 4 ( t ) - ( в 31 + в32 + в 34 ) Р 3 ( t ), Р 4 ( t ) = в 4 Р 1 ( t ) + в 24 Р 2 ( t ) + в 34 Р 3 ( t ) - ( в 41 + в + в 43 ) Р 4 ( t ),

_ Р 1 ⁽ t ) + Р 2 ⁽ t ) + Р 3 ⁽ t ) + Р 4 ⁽ t ) = 1.

Обозначая через у₁ = в ₁₃ + в ₁₂ + в ₁₄; Y ₂ = в ₂₁ + + в 23 + в 24 ; Y 3 = в 31 + в 32 + в 34 ; Y 4 = в 41 + в 42 + в 4 и отбрасывая одно из уравнений системы (7), придем к следующей системе алгебраических уравнений:

• -- Y 1Р 1 ^{+ в} 21 Р 2 ^{+ в} 31 Р 3 ^{+ в} 41 Р 4 = 0,

• ^в 12 ^Р 1 ^Y 2 ^Р 2 ^{+ в} 32 ^Р 3 ^{+ в} 42 ^Р 4 ⁰ ,

• ^в 13 ^Р 1 ^{+ в} 23 ^Р 2 - ^Y 3 ^Р 3 ^{+ в} 43 ^Р 4 = ⁰ , . Р 1 ⁺ Р 2 ⁺ Р 3 ⁺ Р 4 = ^1.

  
  

Разрешая эту систему относительно неизвестных вероятностей, получим следующие рас- четные формулы для указанных вероятностей:

= £ 1 6 22 ^{- 6} _п ^£ 2 p¹    5 11 § 22 - 6 12 6 21’

6 12 = в 41 - в 21

6 21 = в 42 - в 12

( в 41 - в 31 )( в 43 - в 23 ) Y 3 ^{+ в} 43

в - в 32 )( в 43 - в 13 )

Y 3 ^{+ в} 43

Р43    Р43 - в  „ в43 - в р^ =---Р--Р^

Y 3 + в 43    Y 3 + в 43 Y 3 + в 43

Р 4 = ¹ - Р 1 - Р 2 - Р 3 ,

6 22 = Y 2 + в 42

^£ 1 = ^в 41 -

( в 42 - в 32 )( в 43 - в 23 ) Y 3 ^{+ в} 43

( в 41 - в э1 ) в 43

Y 3 ^{+ в} 43

ВЕСТНИК 2013 № 4

или в более развернутом виде для вероятностей

p, p, p: 2  3  4 6   61 p2 =   2      ^1 • 2   622   622 Аз Рз =    4" Y3 + в43 в43 - в23  [ £1622 - 612£2 . 611622 - 612621; в43 - в13  £1622 - 612£2 • Y3 + в43  611622 - 612 621 £1622 - 612£2 \ (Y3 + в43 )622 1 £ Р 4 = 1 622   Y £1622 ~ 612£2 6ц622 - 612621 ;2  "216П622 - 612621 j; в43 + в43 <1 - 621 - в43 - в13 J + (   622   Y3 + в43 ) в43 - в23

^{+ в} 43 ^{) 6} 22

^£ 1 ⁶ 22    ⁶ 12 ^£ 6 2

6 11 6 2 2 - 6 2 6 2,

_р о _ ( в 42 - в 32 ) в 43

^£ 2     ^в 42           , _п

^Y 3 ^{+ в} 43

.

Теперь о величинах коэффициентов β_ij . Коэффициенты β_ij представляют собой вероятность «передачи» сейсмодеформационной энергии из области i в область j , т.е. величины, рассчитываемые по соотношению (6). Описанная схема позволяет, по нашему мнению, установить вероятностную траекторию движения сейсмоде-формационной энергии (ее миграции) в геосреде вдоль тектонических разломных нарушений.

где 6 11 = Y 1 + в 41

( в 41 - в э1 )( в 43 - в 1э )

Y 3 ^{+ в} 43

Результаты использования обобщенной вероятностной модели

В первую очередь рассмотрим результаты, полученные по обобщенной вероятностной модели для региона, в пределах которого предполагается строительство АЭС около города Гюльнар в Турции (г. Гюльнар обозначен на карте-схеме окружностью с шестью исходящими лучами) (рис. 4).

30             31             32             33             34             35             36

Век. к:

ifiuMre1*""’ Л^тг<^~ S f,X4»-^           -* b ”   ^_ . -^

UliUflnai

30             31

ktiDkl., Episkopi

.< 1^ B3hai"3(

32            33            34            35            36

Рис. 4. Карта-схема эквипотенциального распределения вероятностного геодинамического риска (вероятностный геодинамический риск – риск, определяемый не в плане его энергетической характеристики, а в плане вероятности реализации опасного геодинамического, в нашем случае, сейсмического события) для региона предполагаемого размещения АЭС «Аккую»

Области геодинамического риска оконтурены изолиниями в диапазоне от 0.1 до 0.9 с шагом значений 0.2. Кружками обозначены эпицентры уже произошедших за период времени с 528 г. по май 2010 г. в этом регионе землетрясений с магнитудами от 4 до 7 (всего 232 сейсмических события).

Незакрашенными квадратами указаны эпицентры пяти исторических высокоэнергетических землетрясений на территории, прилегающей к Турции, взяты из информационной базы Мирового центра данных по физике твердой Земли, охватывающей период с 2100 г. до н.э. по 1992 г. н.э.

Время событий, координаты и сила землетрясений следующие: 13.12.115 г. н.э. (координаты 35.°8 северной широты (с.ш.), 35.°1 восточной долготы (в.д.), магнитуда М = 7.5); 13.02.1404 г. н.э. (35.°7 с.ш., 36.°2 в.д., М = 7.0); 30.12.1408 г. н.э. (35.°8 с.ш., 36.°1 в.д., М = 7.5); 04.05.1875 г. н.э. (35.°1 с.ш., 30.°2 в.д., М = 7.3); 03.10.1914 г. н.э. (37.°9 с.ш., 30.°1 в.д., М = 7.1).

Черным закрашенным квадратом обозначен эпицентр катастрофического землетрясения 08.04.859 (35.º9 с.ш., 36.º0 в.д., М = 8.0).

Как видно на рис. 4, пространственное рас- пределение вероятностного геодинамического риска достаточно значимо согласуется с распределением выделившейся сейсмической энергии в рассматриваемом регионе, что свидетельствует об адекватности математической модели, использованной для количественной оценки указанного риска. В окрестности г. Гюльнар (места предполагаемого строительства АЭС «Аккую») геодинамическая ситуация потенциально опасная (вероятность реализации опасных геодина-мических процессов порядка 0.7).

Подобная модель была нами применена и к исследованию РПТС, включающей территорию Эквадора и части территорий сопредельных с ним государств. Исследовательский интерес к этому латиноамериканскому государству обусловлен следующим.

Северные Анды, как и вся Андийская система, относятся к сейсмически активным зонам Земли. Так, в 1949 г. в Эквадоре город Пе-лилео был полностью уничтожен в результате землетрясения мощностью 6,8 балла по шкале Рихтера, а в 1999 г. значительным разрушениям подверглись крупные колумбийские города Армения и Перейра.

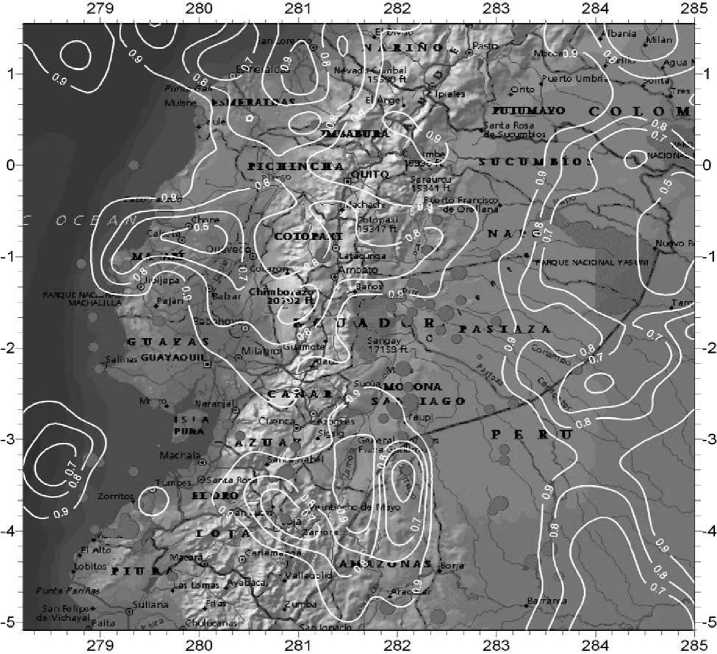
Рис. 5. Карта эквипотенциального распределения вероятностного геодинамического риска для территории Эквадора и прилегающих к нему государств с эпицентрами произошедших за период 1970–2011 гг. землетрясений

ВЕСТНИК 2013 № 4

ВЕСТНИК 2013 № 4

Между двумя горными цепями Эквадора расположена приподнятая до 2500–2700 м тектоническая депрессия с полосой разломов, вдоль которых поднимаются потухшие и действующие вулканы. Самые высокие из них – вулкан Пи-чинча (4794 м) и потухший вулкан Чимборасо (6130 м). В пределах этой тектонической депрессии на высоте 2700 м расположена столица Эквадора – Кито.

Совсем недавно вулканы заставили серьезно поволноваться население Эквадора и в особенности ее столицы – Кито. В декабре 2012 г. правительство этой небольшой латиноамериканской страны объявило в провинциях Тунгурауа и Чимборасо высокий – «оранжевый» – уровень вулканической опасности. И все из-за повышенной активности вулкана Тунгурауа, расположенного всего в 135 км от столицы. Предыдущие извержения этого вулкана были зафиксированы в апреле и августе 2012 г., а последнее крупное извержение Тунгурауа произошло семь лет назад. Тогда его жертвами стали шесть человек, все – жители расположенного у подножия горы поселка. В 1999 г. из-за извержения власти эвакуировали из опасных районов около 15 тысяч человек.

Учитывая эти последние события, нами предпринята попытка оценки геодинамической устойчивости среды территории Эквадора и прилегающих к нему государств.

На рис. 5 изображено эквипотенциальное распределение вероятностного геодинамическо-го риска для территории Эквадора с эпицентрами произошедших за период 1970–2011 гг. землетрясений. Области, оконтуренные изолиниями со значением вероятности 0.5, определены как зоны латентно-потенциального риска; 0.7 – зоны умеренного риска; 0.8 – зоны повышенного риска; 0.9 – зоны чрезвычайной опасности.

Эта карта, с нанесенными на нее эпицентрами землетрясений, также наглядно демонстрирует эффективность и работоспособность обобщенной математической модели: эпицентры произошедших землетрясений «легли» как раз на те участки территории, которые определены по модели как наиболее опасные в геодинамиче-ском отношении.

Еще раз подчеркнем, что карты, подобные представленным на рис. 4 и рис. 5, отражают не интегральную вероятность сейсмического риска для всего региона в целом, а именно «точечноплощадную» вероятность проявления сейсмических событий. Размеры таких «точечных» площадок зависят от линейной протяженности исследуемой территории, сводясь к территориям порядка нескольких квадратных километров или даже сотен метров.

Заключение

Невзирая на колоссальные усилия, предпринимаемые исследователями во всем мире, точный временной прогноз землетрясений и, в особенности, катастрофических землетрясений на сегодняшний день пока остается тайной за семью печатями, поскольку динамика опасных природных явлений до сих пор не укладывалась в прокрустово ложе современной прикладной математики.

Полагаем, что небольшим вкладом в решение этой актуальнейшей проблемы является предложенная обобщенная вероятностная модель оценки геодинамической устойчивости среды распределенной природно-технической системы, позволяющая учитывать в явном виде распределение на исследуемой территории РПТС тектонических разломных нарушений и других неоднородностей геологической среды.

Дальнейшее развитие модели позволит, по нашему мнению, установить вероятностную траекторию миграции сейсмодеформационной энергии, что выступает весьма значимым в прогностическом смысле результатом.