Обобщенная весовая интегрируемость мультипликативных преобразований Фурье
Автор: Голубов Б.И., Волосивец С.С.
Журнал: Труды Московского физико-технического института @trudy-mipt
Статья в выпуске: 1 (9) т.3, 2011 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/142185725
IDR: 142185725
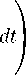
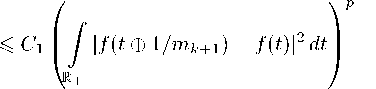
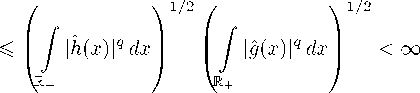
Список литературы Обобщенная весовая интегрируемость мультипликативных преобразований Фурье
- Golubov B.I., Volosivets S.S. On the integrability and uniform convergence of multiplicative Fourier transform//Georgian Math. J. { 2009. { V. 16, N 3. { P. 533{546.
- Onneweer C., Waterman D. Uniform convergence of Fourier series on groups // Mich. J. Math. { 1971. { V. 18, N 3. { P. 265{273. 5. .®«®á¨¢¥æ .... ਡ«¨¦¥¨¥ äãªæ¨© ®£à - ¨ç¥®© p-ä«ãªâã 樨 ¯®«¨®¬ ¬¨ ¯® ¬ã«ì⨯- «¨ª â¨¢ë¬ á¨á⥬ ¬ // Anal. Math. { 1995. { V. 21, N 1. { P. 61{77.
- Gogoladze L., Meskhia R. On the absolute convergence of trigonometric Fourier series//Proc. Razmazde Math. Inst. { 2006. { V. 141. { P. 29{40.
- Moricz F. Su cient conditions for the Lebesgue integrability of Fourier transforms//Anal. Math. { 2010. { V. 36, N 2. { P. 121{129.
- Izumi M., Izumi S. On absolute convergence of Fourier series//Arkiv. Mat. { 1967. { V. 7, N 12. { P. 177{184.
- Izumi M., Izumi S. Absolute convergence of Fourier series of convolution function//J. Approx. Theory. { 1968. { V. 1, N 1. { P. 103{109.
- Onneweer C.W. On absolutely convergent Fourier series//Arkiv. Mat. { 1974. { V. 12, N 1. { P. 51{58.
- Onneweer C.W. Absolute convergence of Fourier series on certain groups // Duke Math. J. { 1974. { V. 41, N 3. { P. 599{610. 13. .®«®á¨¢¥æ .... . á室¨¬®á⨠à冷¢ ¨§ ª®íää¨æ¨¥â®¢ .ãàì¥ ¬ã«ì⨯«¨ª ⨢ëå ᢥà- ⮪ // .§¢. ¢ã§®¢. . ⥬. { 2008. { ü 11. { .. 27{ 39.
- Aljancic S., Tomic M. Uber Stetigkeitsmodul von Fourier-Reihen mit monotonen Koe zienten // Math. Zeitschrift. { 1965. { V. 88, N 3. { S. 274{284. 15. .®«®á¨¢¥æ ...., .®«ã¡®¢ ... .¥á®¢ ï ¨- ⥣à¨à㥬®áâì ¬ã«ì⨯«¨ª ⨢ëå ¯à¥®¡à §®¢ - ¨© .ãàì¥ // .à. ..€. { 2010. { .. 269. { .. 71{ 81. 16. .ª¢®à殢 ..€. .¥®à¥¬ ¥¤¨á⢥®á⨠¯à¥¤áâ ¢«¥¨ï äãªæ¨© ¬ã«ì⨯«¨ª ⨢묨 ¯à¥®¡à §®¢ ¨ï¬¨ // .¥á⨪ .... .¥à. 1. . ⥬., ¬¥å. { 1992. { ü 6. { C. 14{18.
- Young L.C. An inequality of the Holder type connected with Stieltjes integration // Acta Math. { 1936. { V. 67. { P. 251{282. 18. ¤¢ à¤á . ï¤ë .ãàì¥ ¢ ᮢ६¥®¬ ¨§- «®¦¥¨¨. .. 2. { ..: .¨à, 1985. 19. .ìï祪® ...., .«ìﮢ ... .¥à ¨ ¨- â¥£à «. { ..: . ªâ®à¨ «, 1998. 20. .¨âç¬ àè .. .¢¥¤¥¨¥ ¢ ⥮à¨î ¨â¥£à - «®¢ .ãàì¥. { ..: .®áâ¥å¨§¤ â, 1948. 21. .¨£¬ã¤ €. .ਣ®®¬¥âà¨ç¥áª¨¥ àï¤ë. .. 1. { ..: .¨à, 1965. 22. ¥á¯ «®¢ .... .¯¥à â®àë ¬ã«ì⨯«¨ª - ⨢®£® ¯à¥®¡à §®¢ ¨ï .ãàì¥ // .§¢. ¢ã§®¢. . - ⥬. { 2006. { ü 3. { C. 9{23.
Статья
