Обобщенное пространственно-матричное выражение энергии сигнала на выходе нелинейного модулятора
Автор: Батенков Кирилл Александрович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 3 т.11, 2013 года.
Бесплатный доступ
Получено выражение энергии сигнала на выходе нелинейного модулятора. Доказано, что она однозначно определяется структурой модулятора и матрицами начальных моментов сигнала на его входе от первого до порядка, соответствующего удвоенной степени нелинейности модулятора.
Нелинейный модулятор, энергия сигнала, пространственная матрица, плотность вероятности, разложение в ряд
Короткий адрес: https://sciup.org/140191653
IDR: 140191653 | УДК: 621.391.83
Текст научной статьи Обобщенное пространственно-матричное выражение энергии сигнала на выходе нелинейного модулятора
Известна проблема введения энергетического ограничения на входы канала связи или выходы модулятора. Для операции демодуляции характерно стремление приблизить векторы на его выходе к исходным передаваемым векторам, что выливается в локализацию выходных сигналов вблизи области определения передаваемых сигналов. При этом степень локализации, определяющая точность воспроизведения информации, напрямую связана с соотношением между неопределенностью, вносимой каналом связи, и неопределенностью, обусловленной стохастич-ной природой самой информации. Поскольку оператор модуляции позволяет формировать сигналы на его выходе в общем случае произвольным образом, то естественно, что оптимальное решение будет соответствовать произвольно большому разнесению между различными передаваемыми сигналами. Данное обстоятельство приводит к необходимости использования бесконечно большой мощности (энергии) для фор- мирования сигналов на выходе модулятора, что приводит к невозможности реализации подобных преобразований на практике. В результате следует рассматривать дополнительное ограничение на мощность (энергию) передаваемых сигналов по каналу связи.
Функциональная форма выражения энергии сигнала на выходе нелинейного модулятора
Энергию сигнала на выходе модулятора возможно представить в виде разности
^ = J J ^х" cox^x;;t,r^dxdtdr - t Г X
x;t,r^dxdtdv,
где – одномерная плотность распределения вероятностей значений сигнала на выходе модулятора x ( t , r ), задающая вероятностную меру в некоторой точке пространства r в определенный момент времени t ; – среднее значение сигнала на выходе модулятора определяется как первый начальный момент определенного сечения данного случайного поля x ( t , r ):
В соответствии с условием нормировки плотностей вероятности вычитаемое в (1) преобразуется в интеграл лишь по переменным времени и пространственным координатам. Детерминированность разложения в обобщенный ряд Фурье выходного сигнала модулятора позволяет представить условную плотность его сечений по времени и пространственным координатам относительно сечений по множеству координатных функций #>г)=кОД ^iM -Г, где Т означает операцию транспонирования как дельтафункцию, а на основании формулы полной вероятности плотность распределения пространственно-временных сечений принимает форму coY(x;/,r)= J§[x - хг\|/(?,г)]озл.(х)бй. (3)
Для устранения неоднозначности обозначение плотности распределения выходного сигнала в виде пространственно-временных сечений co^x^r) дополнительно используют в качестве аргументов соответствующие координаты t и r, а в форме коэффициентов разложения Юг(Х) – только случайные переменные x . В дальнейшем, если не возникает противоречий, указание на тип сечений не производится, в формулах же отсутствие аргументов с пространственными и временными координатами однозначно идентифицирует сечения как коэффициенты разложения. Математическое ожидание выходного сигнала модулятора имеет вид скалярного произведения бесконечномерных векторов:
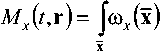
•ХГ6^-\|/(/,г)
Использование (3)-(4) и фильтрующего свойства дельта-функции в (1) преобразует энергию выходного сигнала модулятора в форму:
Линейность операции интегрирования дает возможность представления формулы энергии в виде разности квадратичных форм:
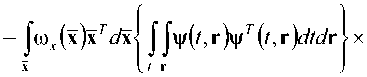
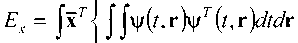
>x«>x(x)dx -
Поскольку полная система координатных функций vM произвольна, то без потери общности она может быть выбрана ортонормиро-ванной:
j* J\|/(/, r)^'//, r )<://c/r = E ,
где E – единичная матрица. В результате энергия выходного сигнала демодулятора определяется в виде разности сумм вторых начальных моментов коэффициентов разложения сигнала и квадратов первых, то есть сумм дисперсий коэффициентов разложения сигнала в системе координатных функций Ч'(М'):
Ex = tr(MTJ-M^MTj,
где tr(A) – след двумерной матрицы A, являющийся, по сути, суммой ее диагональных элементов [1]; M^' {^«,,--4, – i-мерная матрица порядка ∞ начальных моментов i-го порядка сигнала на выходе модулятора x, элементы которой определяются как математические ожидания соответствующих произведений [2]:
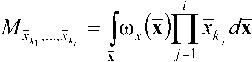
Матрицу начальных моментов можно представить в виде
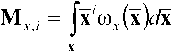
где x' = XX ...X X – i-кратное прямое (декартово) произведение векторов x [3-4], задающее пространственную матрицу со всевозможными комбинациями элементов, входящих в данные векторы, то есть для произвольных пространственных матриц А=и„...л} и B={^^J их прямое произведение формирует матрицу A x В — ^^^jB^ +1 |$ размерность которой равна сумме размерностей исходных матриц A и B.
В дальнейшем для устранения неоднозначности в описании прямого произведения и произведения двумерных матриц для двумерных матриц символ «×» используется только при переносе формулы с одной строки на другую, о чем обязательно упоминается по тексту. Тип операции возведения в степень оговаривается непосредственно до или после первого применения этой операции в выражении и последующих его мо- дификаций. Для векторов и многомерных матриц (размерности большей двух) возведение в степень всегда соответствует кратному прямому произведению.
^^ Л", 1 ^^J ^^^ / ^ ^ 5 • • • 9 ^" }^ ^^Х (^ ^Z^X . (15)
-=1 X
Матричная форма выражения энергии сигнала на выходе нелинейного модулятора
Нелинейность оператора модуляции позволяет представить (15) в форме сумм произведения пространственных матриц:
Коэффициенты разложения базисных фун-
кций модуляции целесообразно представить в
виде ( i + 1)-мерной матрицы переменного порядка Ф‘ — {^....^jL,,..^!^,;^,^ у которой только элементы с неубывающими индексами, за исклю-
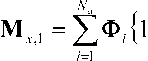
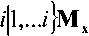
где
чением последнего, могут быть отличны
от
нуля, то есть
Фкхк,,] =0| 3ki <кГ’ l
a{/„...,z,,|/6,.../6,}b =
Ф, есть
N х ...х N хш
'----v----- . Тогда бесконечномерная
плотность распределения вероятности сигнала на
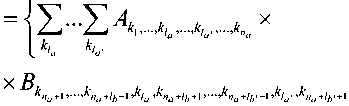
–
выходе модулятора имеет вид
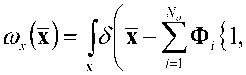
z}x где введено упрощенное описание произведения пространственной матрицы ф, на вектор x: N N N Ф,{1,-,/}х = ^^„. ^=1 к^-к^ k-^kj. Одномерная же плотность вероятности сигнала на выходе модулятора задается в форме (x)z7x, (13) произведение na-мерной матрицы АПЛ.....^) на nb-мерную !$-{/>•,.....к„ь} одинакового порядка по индексам =1,« у первой матрицы A и kv-Jb' - кпь у второй B, результатом данной операции является матрица с размерностью, равной сумме размерностей исходных матриц за вычетом числа индексов, по которым осуществляется произведение для одной из матриц; где Ф/д = ) ФА.к. ,к / , , . , к = L со – сечение А )kl,...,kj=l,N ориентации k (i + 1)-мерной матрицы Ф„ по сути являющееся совокупностью элементов матрицы Ф, при фиксированном значении последнего индекса k, то есть i-мерной матрицей. Математическое ожидание сигнала на выходе модулятора определяется как Соответственно, саму матрицу начальных моментов возможно представить в виде, аналогичном (10): Мл,, (х)б/хг/х. (14) мх,- = |х'юх(х)б/х. Учитывая фильтрующее свойство дельта-функции, внешний интеграл сокращается, а линейность суммирования и интегрирования приводит к следующему виду математического ожидания сигнала на выходе модулятора: Для произвольных пространственных матриц A, B и С возможно показать выполнимость аналога ассоциативного свойства: (a^J^^b)^]^ }с = [(а{а3 |а4 Jefe - 1|а-2 }в Jdim A-'--d,m A+d,m c"3) k3< dim A, k3< kx, [(a^ + fe4 Jefe |^2}b Jdim A-1-"dim A+dim c"3) £3 A^fe — 1X®{^з “dim A + fe4Jc), k3 > dim A, k3 - dim A +1 < k2, AX \k2 jfefe - dim A + 2|A4 Jc), k3 > dim A, k3 - dim A +1 > k2, где dim A – размерность произвольной матрицы A; A^'1-■*„ – оператор транспонирования пространственной матрицы аЧА^^л! соответственно перестановке индексов к, ,...,k на последние позиции, то есть n< dim A. Следует отметить, что если C является вектором (dim C = 1), то в (20) для k3< dim A операция транспонирования не выполняется, так как единственное измерение C сокращается при выполнении пространственного произведения. Кроме того, справедливо и дистрибутивное свойство A{ kx \k2 }(B + С) = Х^кх \k2}b + a{ ^ |^2 Jc. (22) Для двумерных матриц A и B справедливы следующие тождества: a{l|l}b = a{l}b = arb , (26) а для одномерного вектора a и двумерной матрицы A: Операция же транспонирования, примененная к некоторому вектор-столбцу a = Ut}, по сути, преобразует его в матрицу a={a,J с одной строкой, число столбцов которой соответствует числу элементов вектора a: Отсюда следует, что пространственное произведение оказывается частным случаем (17) при условии одномерности матрицы, на которую производится умножение. Таким образом, вектор математических ожиданий сигнала на выходе модулятора Mx,1 полностью определяется структурой модулятора Ф„ i = l,Na и матрицами начальных моментов сигнала на его входе Mx,i от первого до порядка, соответствующего степени нелинейности модулятора Na. Сумма начальных моментов второго порядка сигнала на выходе модулятора trMx,2 вычисляется как Применение фильтрующего свойства дельтафункции позволяет сократить внешний интеграл, а линейность операций интегрирования и суммирования преобразует (32) к виду N„ N„ trM.v.2=££(o>l|7 + l}J /=1 ./=1 {1„..,z + 7|1„..,7 + 7}mx_/+/. Аналогичным образом получается вычитаемое в формуле энергии выходного сигнала модулятора (8) на основе (16): м1дМхД=^£(ф^.^1,^Мх,г) ,=1 y=l A {2|l}a = Afea = Aa, A{l|l}a = A{l}a = Ara. Аналог ассоциативного свойства и скаляр-ность (8) приводит к следующему результату: Для операции транспонирования двумерной матрицы A выполняются следующие равенства: A« = А<2Д) = Ar ,(29) a(2) = a(l2) = a.(30) М^МхЛ=££(фД/^7 + 1}Ф7). M(35) {1„.„z + 7|1„..,z + 7)(mXj,.MxJ. Подстановка (33) и (35) в (8) и использование свойства дистрибутивности трансформирует вы- ражение для энергии выходного сигнала модулятора к виду: £х-££(ф;?+1к1}ф/) z=i ;=i {l,...,z + v|l,...,z + 7Хмх_/+/ -MXJMX J Заключение В работе получено общее выражение для энергии сигнала на выходе модулятора в виде пространственно-матричного произведения. Доказано, что энергия сигнала на выходе модулятора однозначно определяется структурой модулятора Ф„ i = VNa и матрицами начальных моментов сигнала на его входе Mx,i от первого до порядка, соответствующего удвоенной степени нелинейности модулятора Na.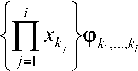
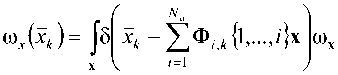
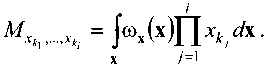
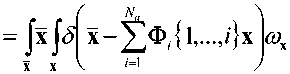
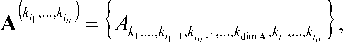
A {2 1 }b = AB,
(23)
A {1 1 }B = A B,
(24)
A{l,21,2}B = tr(AB),
(25)
для одномерного случая векторов a и b:
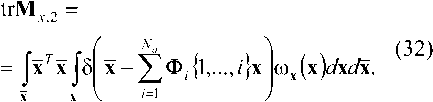
Список литературы Обобщенное пространственно-матричное выражение энергии сигнала на выходе нелинейного модулятора
- Магнус Я.Р., Нейдеккер Х. Матричное дифференциальное исчисление с приложениями к статистике и эконометрике. Пер. с англ. М.: Физматлит, 2002. -496 с.
- Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устойчивых систем. М.: Радио и связь, 1991. -608 с.
- Корн Г., Корн К. Справочник по математике для научных работников и инженеров. М.: 1970. -720 с.
- Морозова В.Д. Введение в анализ. М.: Изд. МГТУ им. Н.Э. Баумана, 1996. -408 с.


