Обобщенные турниры-перевертыши

Чемпионат России 2006 г. по футболу выиграл футбольный клуб ЦСКА. «Спартак» набрал то же количество очков, что и армейский клуб, но уступил конкуренту по дополнительным показателям. Однако болельщики «Спартака» утверждают, что именно их любимая команда, была, сильнее всех. Ведь система, подсчета очков, при которой за победу команде начисляется 3 очка, за. ничью — 1 очко, а. за. поражение — 0 очков, была, введена, относительно недавно. Если же подсчитать очки по старой системе, при которой за победу начислялось всего 2 очка, то «Спартак» окажется впереди ЦСКА на. целых три очка. Болельщики армейцев резонно возражают, что регламент первенства был утвержден заранее и известен всем участникам.

Автор не берется рассудить болельщиков, полагая, что они никогда не придут к консенсусу. Предыдущий пример приведен лишь для того, чтобы проиллюстрировать очевидный факт: при подсчете очков по разным системам итоговые таблицы одного и того же турнира могут существенно отличаться. Наша цель – выяснить, что же скрывается под словом «существенно». Могут ли участники первенства в результате перехода к другой системе подсчета очков расположиться в итоговой таблице в обратном порядке?

Дабы не погрязнуть в сравнении дополнительных показателей (количество побед, разность забитых и пропущенных мячей, результаты личных встреч команд, набравших одинаковое количество очков), которые меняются от соревнования к соревнованию, договоримся рассматривать лишь такие турниры, в которых никакие две команды не набрали поровну очков. Такие турниры мы будем называть «строгими». Если в строгом турнире при подсчете очков по старой системе участники выстраиваются определенным образом, а при новой системе – в обратном порядке и строгость турнира сохраняется, то такой турнир будем называть «перевертышем».

Таблица 1

Количество команд (n)	Число кругов (—k)
2	-
4	13
3	10
6	9
5, 8	8
7, 9, 10, 12, 14, 16	7
остальные n > 1	6

В работе [2] автором совместно с И. Г. Шевчуко-вым описаны минимальные возможные параметры турниров-перевертышей для случая, когда, сравниваются результаты по старой и действующей системам под- счета очков в футболе. В табл. 1 для каждого возможного количества участников кругового турнира указано минимальное число кругов, при которых данный турнир может оказаться перевертышем.

В настоящей статье результаты работы [2] обобщаются на произвольные системы подсчета очков.

Пусть за победу команде присуждается v, за ничью – s, а за. поражение — f очков. Единственное требование, которому должны удовлетворять эти числа: v > s > f. В остальном же числа v, s, f могут быть совершенно произвольными, в том числе дробными и даже иррациональными. Число c = ( v — f ) /( 5 — f ) назовем характеристикой системы подсчета очков.

Две системы подсчета очков назовем изоморфными, если при поочередном подведении итогов сначала по одной системе, а. затем — по другой команды не меняют своих позиций в итоговой таблице любого турнира. Не трудно доказать, что две системы подсчета, очков изоморфны тогда и только тогда, когда их характеристики равны.

В каждом классе изоморфных между собой систем с данной характеристикой c имеется система, подсчета, очков, в которой f = 0, 5 = 1, v = c . Такие системы будем называть нормализованными. Понятно, что достаточно рассматривать лишь нормализованные системы. Систему подсчета очков назовем «агрессивной», если c > 2, «миролюбивой» — если c < 2 и «равновесной» — если с = 2. Таким образом, старая система подсчета очков в футболе является равновесной, а новая – агрессивной.

Пусть с 1 и с₂ характеристики двух систем подсчета, очков и с 1 < c₂. Для удобства, и по аналогии с ситуацией в футболе будем называть систему подсчета с характеристикой с¹ старой, а с характеристикой c₂ – новой. Нумеровать команды будем в соответствии с местами, занятыми по старой системе.

Предположим, что в турнире участвует n команд и соревнование проводится в k кругов (то есть каждая команда. встречается с каждой к раз). Наша, цель выяснить, при каком наименьшем k переход от системы с₁ к системе c₂ может (при подходящем n) перевернуть турнирную таблицу. Может показаться (автору поначалу так и казалось), что количество кругов в турнире-перевертыше будет тем больше, чем меньше отличаются друг от друга, числа. с 1 и c₂. Однако зависимость оказалась несколько иной.

Пусть u и hv такие наименьшие натуральные числа, что uс¹< h < uс², a w = k - u . Тогда i -я команда должна иметь в турнире-перевертыше, по крайней мере, на u побед меньше и на. h ничьих больше, чем команда, занявшая i+1-е место. Рассмотрим столбцы итоговой таблицы турнира-перевертыша, в которых представлены суммарные показатели выигрышей, ничьих и поражений для каждой команды (табл. 2).

Таблица 2

¹	Выигрыши	Ничьи	Поражения
1	v(1)	s(1)	f(1)
2	v(2)	s(2)	f(2)
3	v(3)	s(3)	f(3)
...........................
n	v(n)	s(n)	f(n)

Пусть v ( i ) = v ( i +1) - u, s ( i ) = s ( i +1) + h, f ( i ) = f ( i +1) - w для всех допустимых i, т.е. различия между показателями в соседних стоках таблицы достигают наименьших возможных значений. Ясно, что X ” _{= 1} v ( i ) = X "=\f ( i ). Отсюда, учитывая, что v(i) и f(i) — арифметические прогрессии, получаем v(1) + v(n) = f (1) + f (n) . Но v ( n ) = v (1) + ( n -1) u и f ( n ) = f (1) + ( n —1)( h — u ). Поэтому

v(1) = (2f (1) + (n - 1)(h - 2u)/2 >  (n - 1)(h - 2u)/2 . (1)

Посчитаем двумя способами общее число матчей, сыгранных первой командой в k-круговом турнире: ( n -1) k = v (1) + s (1) + f (1) >  v (1) + ( n -1) h . Учитывая соотношение (1), получим оценку снизу для числа кругов ([ x ] — потолок числа x, т.е. наименьшее целое, не меньшее x):

k > Г (3 h - 2 u )/2 ^. (2)

Получая неравенство (2), мы пренебрегли величиной f(1), положив ее равной 0. Рассуждая аналогично, но на этот раз пренебрегая величиной v(1), получим еще одну оценку для числа кругов в турнире-перевертыше:

k > Г (3 h - 2 w )/2 ^ . (3)

Пусть d = min( u , w ). Тогда, неравенства. (2) и (3) можно объединить:

k > Г (3 h - 2 d )/2 ^ . ⁽⁴⁾

Отметим, что если 2 <  c 1 < c ₂, то u <  w и неравен -ство (4) равносильно (2). Если , то w < u и (4) равносильно (3). Наконец, если c 1 < c 2 < 2, то h=2, u=w=1 и неравенства (2) и (3) дают одну и ту же оценку k ≥ 3 .

Доказательство достижимости оценки (4) наиболее просто именно в последнем случае. Для любых c ₁< 2 <  c ₂ существует 3-круговой турнир-перевертыш уже при n = 5. Табл. 3 показывает, как он устроен.

Отметим, что с₁ и c₂ могут отличаться на сколь угодно малую величину. Главное, чтобы одна из этих характеристик была меньше 2, а другая – больше. Перейдем к рассмотрению случая 2 <  c 1 < c ₂. Если h нечетно, то построение таблицы турнира-перевертыша является естественным обобщением случая c ₁ = 2, c ₂ = 3 , рассмотренного в работе [2]. Докажем, что к = (3 h +1 - 2 и ) / 2 является для нечетных h точной нижней границей k.

Возьмем n = 2 h +1. Пусть x(i,j), y(i,j) и z(i,j) — количества, выигрышей, ничьих и поражений в соответствующих клетках таблицы. Тогда. z(i,j) = k - x(i,j) - y(i,j) , x(j,i) = z(i, j) и y(j,i) = y(i,j). Поэтому достаточно заполнить лишь ту часть таблицы, для которой i <  j , и указать, лишь значения x и y.

Положим:

y(i,j) = h + 1,x(i,j) = k - h - 1 Для j 2 h + 1 ;

y(i,j) = h, x(i,j) = k - h , Для j >  h + 1, i + j 2 n + 1 ;

y(i, j) = 0, x(i, j) = h - u ДЛЯ i 2 h + 1, i + j >  n + 1 и ДЛЯ i >  h + 1, j 2 i + ( h - 1)/2 ; y(i,j) = 0, x(i,j) = h - u + 1 ДЛЯ i >  h + 1, j >  i + ( h - 1)/2 .

То, что в результате получится таблица турнира-перевертыша, проверяется простым подсчетом очков по старой и новой системам. Проиллюстрируем этот случай конкретным примером. Пусть, например, c 1 = 4, c 2 = 5. Тогда, u = 2, h = 9. Поэтому для k = (3 h +1 -2 u )/2 = 12, n = 2 h +1 = 19 существует турнир-перевертыш, представленный в табл. 4.

Рассмотрим теперь случай четного h, большего 2. Для построения турнира-перевертыша, из к = (3 h - 2 и ) / 2 кругов возьмем n = 2 h + 2. Вновь укажем количество побед и ничьих в каждой клетке, расположенной выше главной диагонали. Остальные параметры таблицы легко определяются на основании этих данных.

Положим:

y(i,j) = h + 1, x(i,j) = k - h - 1 для j <  h + 1 ;

y(i,j) = h, x(i,j) = k - h , для j >  h + 1, i + j <  n ;

y(i,j) = 0, x(i,j) = k для i + j = n + 1 ;

y(i, j) = 0, x(i, j) = h - u - 1 для i <  h + 1, i + j >  n + 1 ;

y(i, j) = 0, x(i, j) = h - u для i >  h + 1, j <  i + h /2 ;

y(i, j) = 0, x(i, j) = h - u + 1 для i >  h + 1, j >  i + h / 2 .

Таблица 3

	1	2	3	4	5	Выигрыши	Ничьи	Поражения	Старая система	Новая система
1	X	0 3 0	0 3 0	1 2 0	0 2 1	1	10	1	10+c 1	10+c 2
2	0 3 0	X	0 3 0	0 2 1	2 0 1	2	8	2	8+2c 1	8+2c 2
3	0 3 0	0 3 0	X	2 0 1	1 0 2	3	6	3	6+3c1	6+3c 2
4	0 2 1	1 2 0	1 0 2	X	2 0 1	4	4	4	4+4c 1	4+4c 2
5	1 2 0	1 0 2	2 0 1	1 0 2	X	5	2	5	2+5c 1	2+5c 2

В качестве иллюстрации этого случая построим таблицу турнира-перевертыша для c ₁ = 3.3, c ₂ = 3.5 . Тогда, и = 3, h = 10, к = (3 h - 2 и )/2 = 12 и n = 2 h + 2 = 22 . В общем случае заполняемая часть таблицы разбивается на 12 областей, к каждой из которых применяется свой способ заполнения. Однако при не слишком больших h и u значения в клетках, принадлежащих разным областям, могут оказаться одинаковыми, хотя и рассчитываются по разным формулам. Так, в нашем примере h - u -1 получается равным k - (h - u -1). Поэтому соответствующие области табл.5, задаваемые условиями i < h +1, i + j > n +1 и j < h +1, i + j > n +1, оказываются заполненными одинаково.

Нам осталось рассмотреть ситуацию, когда обе системы подсчета очков не являются агрессивными, т.е. c 1 <  c 2 < 2. Оказывается, построить таблицу турнира, перевертыша для этого случая совсем просто. Пусть uс₁< h < ис 2 . Тогда, w = h - u < u. Временно поменяем местами числа u и w и построим таблицу перевертыша так, как это описано выше. В полученной таблице остается изменить исход каждой встречи на противоположный. Так, табл. 4 может служить примером турнира-перевертыша для c ₁ = 1.25, c ₂ = 1.3, если победы считать поражениями, и наоборот. Таким образом, наши перевертыши еще раз оправдали свое название.

Подведем некоторые итоги. Для любых двух неизоморфных систем подсчета очков существуют турниры- перевертыши. Число кругов в турнире-перевертыше не может быть меньше трех. Трехкруговые турниры-перевертыши существуют в том и только в том случае, когда одна из систем подсчета очков миролюбива, а другая — агрессивна. Наименьшее количество кругов в перевертыше в ситуациях, когда обе системы подсчета очков агрессивны, обе миролюбивы или одна из них равновесна, равно четырем.

Наименьшие число кругов и количество участников турнира-перевертыша, а также его структура полностью определены параметрами h и u . Иными словами, пары характеристик c 1 <  c 2 и c < c 2 могут быть различны, но если наименьшие натуральные h и u, для которых выполняется неравенство ис 1 < h < ис₂, подходят и для пары c‘ , c 2 , то всякая таблица-перевертыш построенная для первой пары характеристик, будет подходить и для второй. Легко видеть, что наименьшие h и u должны быть взаимно просты (иначе они не были бы наименьшими). С другой стороны, для любых взаимно простых натуральных чисел h и u , таких, что h >  u , найдется пара c₁, с₂, приводящая к данным h и u.

В подавляющем большинстве исследованных нами случаев количество участников, равное 2 h + 1 при нечетных и h и 2 h + 2 при четных, является наименьшим n, при котором достигается наименьшее k . Однако в общем случае это не так. Например, при h = 6, и = 1 наименьшее k, равное 8, достигается уже при восьми участниках. В табл. 6 приведен соответствующий пример.

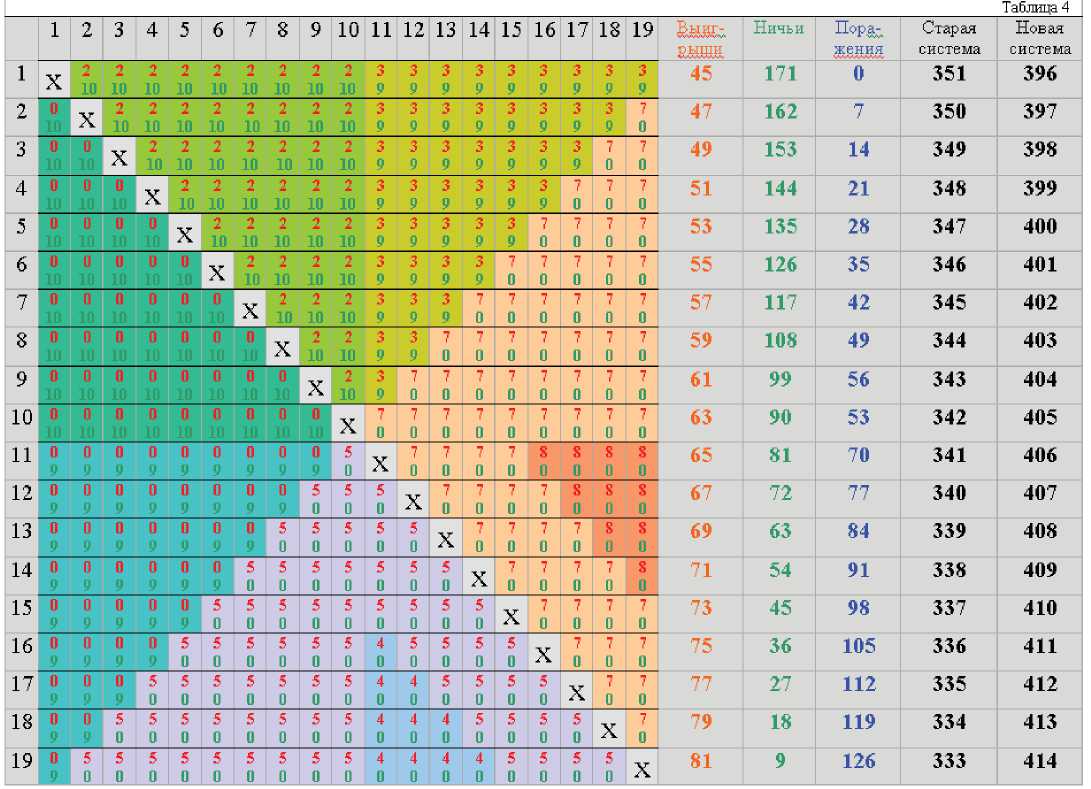
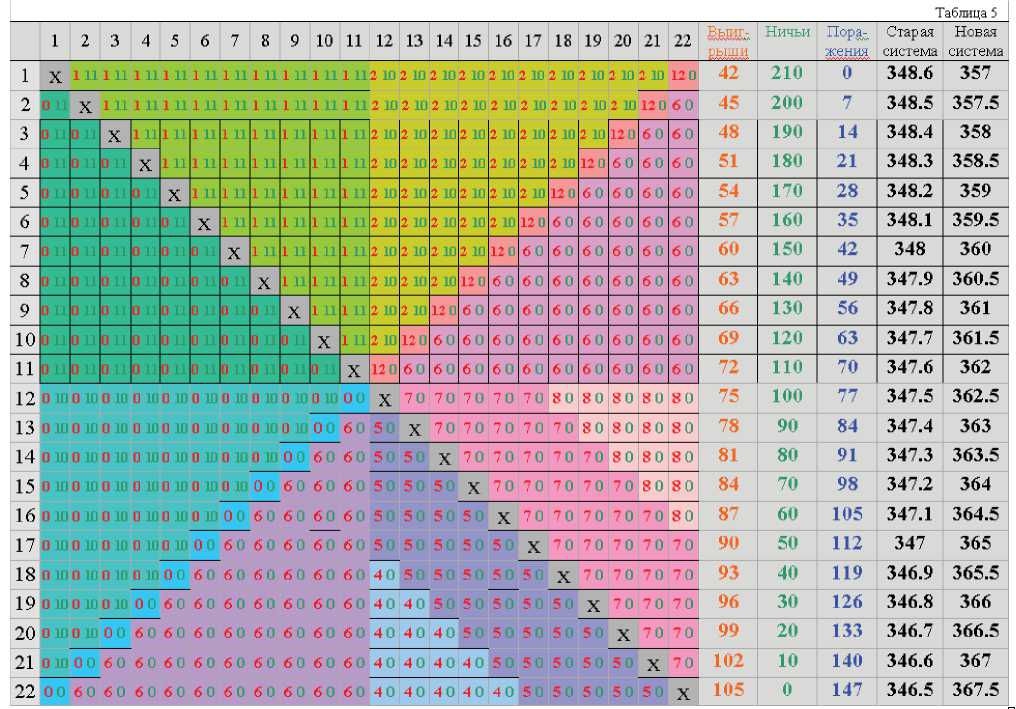
Таблица 6

	1	2	3	4	5	6	7	8	Победы	Ничьи	Поражения
1	X	0 8 0	0 8 0	0 8 0	2 6 0	2 6 0	2 6 0	8 0 0	14	42	0
2	0 8 0	X	0 8 0	0 8 0	2 6 0	2 6 0	8 0 0	3 0 5	15	36	5
3	0 8 0	0 8 0	X	0 8 0	2 6 0	8 0 0	3 0 5	3 0 5	16	30	10
4	0 8 0	0 8 0	0 8 0	X	8 0 0	3 0 5	3 0 5	3 0 5	17	24	15
5	2 6 0	2 6 0	2 6 0	0 0 8	X	6 0 2	6 0 2	6 0 2	18	18	20
6	2 6 0	2 6 0	0 0 8	5 0 3	2 0 6	X	6 0 2	6 0 2	19	12	25
7	2 6 0	0 0 8	5 0 3	5 0 3	2 0 6	2 0 6	X	6 0 2	20	6	30
8	0 0 8	5 0 3	5 0 3	5 0 3	2 0 6	2 0 6	2 0 6	X	21	0	35

Общая формула для нахождения наименьших n для соответствующих k автору не известна.

Так какая же система подсчета очков наиболее справедлива? Автор убежден, что равновесная система является самым объективным мерилом. В свое время в футболе отказались от нее, мотивируя это решение борьбой с договорными ничьими. Но, как говорится, «за что боролись ...». Легко можно представить себе ситуацию, когда команды А и Б в упорной борьбе сыграли вничью оба матча между собой и завоевали по два очка, а команда В без чрезмерного напряжения сил, без травм, предупреждений и удалений победила команду Г на своем поле, а затем «вернула ей должок» на выезде. При этом команды В и Г наберут по три очка и получат преимущество над несговорчивыми А и Б. Анализ некоторых матчей российского первенства и поведения букмекеров показывает, что представленная ситуация не так уж гипотетична. Разумеется, нечистоплотные спортивные функционеры будут изыскивать варианты махинаций при любых системах подсчета очков. Однако в ситуации, когда в каждой встрече разыгрывается фиксированное, не зависящее от исхода количество очков (а это происходит только при равновесной системе подсчета), возможностей для закулисных маневров значительно меньше.