Обобщенный метод скаляризации динамических упругих полей в трансверсально-изотропных средах и его новые применения

Мирошниченко И.П.; Сизов В.П.; Miroshnichenko I.P.; Sizov V.P.

doi:10.23947/1992-5980-2018-18-3-258-264

Обобщенный метод скаляризации динамических упругих полей в трансверсально-изотропных средах и его новые применения

Автор: Мирошниченко И.П., Сизов В.П.

Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu

Рубрика: Механика

Статья в выпуске: 3 т.18, 2018 года.

Бесплатный доступ

Введение. При исследовании тензорных упругих полей перемещений, напряжений и деформаций в слоистых конструкциях из различных материалов, включая трансверсально-изотропные композиты, успешно применяется эффективный метод скаляризации тензорных полей. Данные поля могут быть выражены через скалярные потенциалы, соответствующие квазипродольным, квазипоперечным и чисто поперечным волнам. Такая скаляризация возможна, если рассматриваемые объекты являются тензорами относительно подгруппы общих преобразований координат, когда локальный аффинный базис имеет один инвариантный вектор, который совпадает с осью материальной симметрии материала. При этом в известных работах рассматриваются конструкции, где этот вектор совпадает с нормалью к границе между слоями. Однако, для практики представляют интерес и другие случаи взаимного расположения оси материальной симметрии материала и границы между слоями.Целью является дальнейшее развитие применения метода скаляризации в граничных задачах динамич еской теории упругости на случаи произвольного расположения оси материальной симметрии по отношению к границе между слоями.Методы исследования. Предлагаемый научно-методический аппарат разработан на основе использования обобщенного метода скаляризации динамических упругих полей перемещений, напряжений и деформаций в трансверсально-изотропных средах.Результаты исследования. Получены новые расчетные соотношения для определения полей перемещений, напряжений и деформаций в трансверсально-изотропных средах на случаи произвольного расположения осей материальной симметрии материалов слоев по отношению к границам между слоями.Обсуждение и заключения. Предлагаемый научно-методический аппарат успешно использован при определении напряженно-деформированного состояния в слоистых конструкциях, выполненных из трансверсально-изотропных материалов, и при анализе результатов диагностики состояния плоскослоистых и слоистых цилиндрических конструкций, находящихся в эксплуатации.

Еще

Метод скаляризации, трансверсально- изотропная среда, акустические волны, композиционные материалы

Короткий адрес: https://sciup.org/142214950

IDR: 142214950 | DOI: 10.23947/1992-5980-2018-18-3-258-264

General scalarization method of dynamic elastic fields in transversally isotropic media and its new applications

Introduction. An efficient technique of tensor field scalarization is successfully used while investigating tensor elastic fields of displacements, stresses and deformations in the layered structures of different materials, including transversally isotropic composites. These fields can be expressed through the scalar potentials corresponding to the quasi-longitudinal, quasi-transverse, and transverse-only waves. Such scalarization is possible if the objects under consideration are tensors relating to the subgroup of general coordinate conversions, when the local affine basis has one invariant vector that coincides with the material symmetry axis of the material. At this, the known papers consider structures where this vector coincides with the normal to the boundary between layers. However, other cases of the mutual arrangement of the material symmetry axis of the material and the boundaries between layers are of interest on the practical side.Materials and Methods. The work objective is further development of the scalarization method application in the boundary value problems of the dynamic elasticity theory for the cases of an arbitrary arrangement of the material symmetry axis relative to the boundary between layers. The present research and methodological apparatus are developed through the general technique of scalarization of the dynamic elastic fields of displacements, stresses and strains in the transversally isotropic media.Research Results. New design ratios for the determination of the displacement fields, stresses and deformations in the transversally isotropic media are obtained for the cases of an arbitrary arrangement of the material symmetry axes of the layer materials with respect to the boundaries between layers. Discussion and Conclusions. The present research and methodological apparatus are successfully used in determining the stress-strain state in the layered structures of transversally isotropic materials, and in analyzing the diagnosis results of the state of the plane-layered and layered cylindrical structures under operation.

Еще

Текст научной статьи Обобщенный метод скаляризации динамических упругих полей в трансверсально-изотропных средах и его новые применения

Такая скаляризация возможна, если рассматриваемые объекты являются тензорами относительно подгруппы общих преобразований координат, когда локальный аффинный базис имеет один инвариантный вектор, который совпадает с осью материальной симметрии материала. В [5] рассматриваются конструкции, где этот вектор совпадает с нормалью к границе между слоями. Однако для практики представляют интерес и другие случаи взаимного расположения оси материальной симметрии материала и границы между слоями.

Цель исследования. Целью работы является дальнейшее развитие применения метода скаляриза-ции в граничных задачах динамической теории упругости на случаи произвольного расположения оси материальной симметрии по отношению к границе между слоями.

Постановка задачи. Первоначально в системе координат с допустимым репером находятся компоненты тензоров перемещений и напряжений относительно этого репера. Затем, зная все компоненты тензорных полей в данной системе координат, можно путем перехода к системе координат, связанной с границей между слоями найти нормальные и касательные компоненты перемещений и напряжений, соответствующие площадке, лежащей на границе. Эти компоненты далее используются для удовлетворения граничным условиям задачи [5].

Более подробно изложим вышесказанное на примере решения задач для плоскослоистых конструкций.

Рассмотрим случай, когда главная ось симметрии трансверсально-изотропного материала составляет угол α по отношению к нормали поверхности плоской границы между слоями (рис. 1). При этом считаем, что поле не зависит от координаты y .

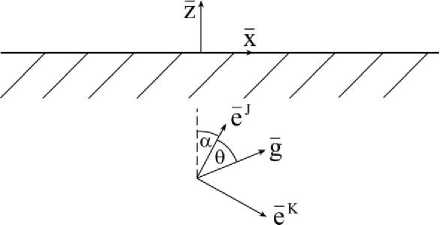
Рис. 1. Расчетная схема

Механика

В соответствии с [4]:

( L ) ( L ) Л

U i = 1 D 1 V i +5 J D ₂ V J |ф +

( T ) 1 ( T )

D VV J + g 5 J

. g

)

w + Vg (5 K V N

-5 N V ^K ) v ;

( L ) ( L ) ( L ) ( L )

_CT jj = ( d 1 g j + d ₂ 5 J 5 ^J + d ₃ 5 J V j ₎ V J + d ₄ V i V j ) ф +

( T ) ( T ) ( T ) ( T )

+ ( d 1 g j V J + d ₂ 5 J 5 ^J V J + d ₃ 5 ^J V j ₎ + d ₄ V i V J V j ) w +

+ 2,/ g [ a 2 ( V₀.3 K , V N -V ₍ , 5 N , V K ) + a ₄( 3 J .3 K , V N -5 J 5 NN , V K ) V j ] v .

Компоненты тензорных полей перемещений U i и напряжений G j в системе координат, связанной с анизотропией материала x ^J , x K , могут быть записаны следующим образом:

( T )

( L ) ( L ) ( L ) ( T ) Р² ( T )

U j = i ^ ( D 1 + D 2 ) ф + ( - D 1 ^ + g ) w ;

( T )( T )

( L ) ( L ) ( T )

U k = i в D 1 ф- D i^ T e w ;

g (2)

(L) (L) (L) (L) (L) ( T) (T) ( T) ( T) ( T) ( T। gJJ = [d1 + d2-(d3 + d4)O + i ^ (d1 + d2+d3-d4 ^2)w;

1 ( L )( L )( L ) ( L )( L )( L ) ( T ) 1( T ) ( T )⁽ T )

^G JK

= - <2 d 3 ^ в + d 4 ^ в ) ф + i в (^ d 3 - d 4 ^) w ;

( L ) ( L ) ⁽ ^L ) ( T ) ( T ) ( T ) ⁽ T )

G KK = ( d 1 + d 4 в ² ) ф + г ^ ( d 1 - d 4 в ² ) w .

Здесь потенциалы квазипро

дольных ф и квазипоперечных w волн должны удовлетворять волновому

( L ) ( T )

уравнению с соответствующ

им волновым числом g ( g или g ) и имеют вид:

( L ) j ( L ) K ф = ф₀ e¹'^^x е^вx ;

( T ) j ( T ) K ( ³⁾

w = w ₀ e‘⁴ ^x е ^вx ,

где 2 ² +в ² = g ² ;

( A + g ²) ^ф= 0. (4)

Входящие в (2) коэф

фициенты D и d , определены в [5] и имеют вид:

( L )

( L ) _______________ g ²( C 13 + C 44 ) _______________ .

¹ ( L ) ( L ) ( L ) ^;

m ² p- h ² C 44 - ( g ² - h ² )( С и - C 13 - C 44 )

( L ) ( L ) ( L ) ( L ) ( L )

( L

_ g_ ™ ² P- h ²(2 C 44 + C 13 ) - ( g ² - h ²) C 11 _ g² ⁽L. ¹ .

( L ) ( L ) ( L ) ( L ) ( L ) ( L ) D ¹ ^;

h ² m ^- _P h ² C 44 - ( g ² - h ² )( С и - C 13 - C 44 ) g ² - h ²

( T )

( ^T )

g _(H3_+V442

^D 1 = ( T ) ( T ) ( T ) ^{; (5)}

m ^; p h ² (2 C 44 + C _n) - ( g ² - h ² ) C_n

( L ) ⁽ ^L)

^d 1 =^- g

⁽ ^L ' ( L ) ( L ) ( L ) ⁽ ^L) ⁽ ^L I ( L ) ( L ) ( L )

a 1 - h a 3 ( D 1 + D ₂); d 2 = - g a 3 - h (2 a ₄ D ₂ + a 5 D 2 + a 5 D 1 );

( L ) ( L ) ( L ) ( L ) ( L ) ( L )
d ₃ = 2 a ₂ D ₂ + 2 a ₄(2 D 1 + D ₂); d ₄ = 2 a ₂ D 1 ;

( ⁽ T )

( T ) ( T ) ( T ) ( T ) h ^{2 (} T )

^d 1 = ^a 1 g ⁽¹ - ^D1) ⁺ ^a 3 g - ^ T ) ^D 1 ;

. g V

( T ) ( T ) ( T ) ( T )

d ₂ = a ₃ g (1 - Dj + 2 a ₄ g + a ₅

f ( T )

( T ) h ² ( T )

g - т ^D1 ^;

(T) (T) (T) (T) h2 (T)(

d3 = 2 a 2 g + 2 a 4 g - 2 D - ; d4 = 2 a 2

. g J a1 = C11 - 2 a 2;

a 2 = ^ ( C „ - C ,2 ) ;

a 3

^- ^ ⁽ ^C 11 ⁺ ^C 12 ^{) +} ^C 13 ⁺ ^C 44 ^- a 4 ^;

a ₄ =

( C 11 - C i ₂ ) + C 44 ; a ₅ = C 11 + C 33 - 2( C _B + 2 C 44 ),

где C ij — модули упругости материала, записанные по свернутому индексу [6-7].

В формулах (5) и (6) для этих коэффициентов:

cos 9 sin 9 _ gz h gz ; в gz ; g / 1 m .

cos( a + 9 ) cos( a + 9 ) cos( a + 9 )

В граничные условия динамических задач теории упругости входят компоненты перемещений U_z , U_x и напряжений 5 _zz , 5 _zx , записанные в системе координат z , x , связанной с границей (рис. 1).

Системы координат z , x и xJ , xK связаны между собой соотношениями [8]: z = -xK sin a + xJ cos a; x = xK cos a + xJ sin a или:

x K = x cos a- z sin a ; x ^J = x sin a + z cos a .

Используя соотношения (8) и (9), по формулам [5]: U -d x m u -d x m d x p

‘ = Sx i Um ; 5 i = 3x1 3x j 5 mp’

где коэффициенты с чертой относятся к системе координат z , x (назовем их «новыми» координатами), а без черты к системе координат x ^J , x K («старые» координаты).

Запишем компоненты полей перемещений U_z , U_x и напряжений условия через компоненты (2):

5 zz , 5 zx , входящих в граничные

U_z = cos a U J - sin a U K ;

U_x = sin a U J + cos a U K ;

⁵ zz = ^cos 2 ^a5 JJ

—

sin2a5„, + sin ² a5,,„ ; JK KK

- 1

⁵ zx = 2sm2 a.⁽⁵ JJ

—

5 kk ) ⁺ ⁽¹ ^- ^2sin ² ^a ) 5 jk .

В «новых» координатах потенциальные функции (3) имеют вид:

( L )

ф __ ф e i К, ( x sin a+ z cos a) e i в ( x cos a- z sin a) ,

( T )

i К (x sin a+z cos a) i в (x cos a-z sin a) w woe e , а перемещения (11) запишутся следующим образом:

( T )

( T)

_ ( L ) ( L ) ( L ) _ ( T ) К ² ( T ) ( L ) ( L ) _

U z = cos a [ i К ( D 1 + D 2 ) ф + ( - D y T ) + g ) w ] - sin a [ i К D 1 ф + ( - D 1 ^ + g ) w ]

( T ) р гл

² ( T )

( T )

( T )( T )

_ ( L ) ( L ) _ ( T ) К ² ( T ) ( L ) ( L ) _ ( L ) КП

U x = sin a [ i ( D ₁ + D ₂) ф + ( - D ₁ ^ T y + g ) w ] + cos a [ i в D ₁ ф- D ₁ —( T j— w ]

Здесь волновые числа К , в , g определены относительно «старого» репера (рис. 2).

Механика

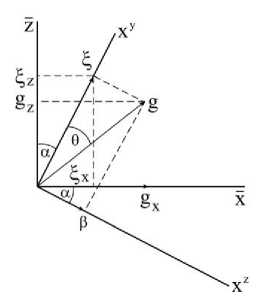
Рис. 2. Схема «взаимосвязи» волновых чисел

Волновые числа £ , в , которые являются проекциями вектора g на «старый» репер x J , x K и волновые числа g x , g z которые являются проекциями вектора g на «новый репер» z , x связаны между собой следующими соотношениями:

_ cos 9 sin( a + 9 ) g x

cos 9

gz; e = cos(a + 9)

sin 9

sin( a + 9 ) g x cos( a + 9 ) ^

¹ z ^;

g =

sin( a + 9 ) cos( a + 9 )

Подставляя (15) в (14), получим выражения для перемещений в «новых» координатах:

■(L ’ cos 9 cos a (L’ (T’ T’

Uz = igz(D1+ D2)ф+gz(-cos 9 D1+ cos(a + 9) cos(a + 9)

_T-_T .⁽ ^L ’cos 9 sin a ,^vb ’ ( L ’. sin 9 cos a ( L ’ ⁽ ^T ’ sin( a + 9 )cos 9 ( T ’ sin a ,_

Ux = ig, [---------(D + D2) +---------D ]Ф + g, [------------D + cos(a + 9) cos(a + 9) cos(a + 9) cos(a + 9)

где, в соответствии с (13) и (15):

_ ( L )_ ( L )_ ( T )_ ( T )_

φ ig x ig x

= ф ₀ e ^g x e^g z ; w = w ₀ e g x e g z

Аналогично, используя (2), (14) и (15), из (12) получим соотношения для компонент напряжений, входящих в граничные условия задач:

- . 2 r( L ’.(L’ . L ’.(L \ cos2 9 (L, Д< L) (L’cos 9 sin 9 (L2. .2 / L’ (L’ sin2 9

CTzz = {cos a[ d + d 2 - (d3 + d4)---Г---— gz] + sin2a(- d 3 + d4) gz + sin a( d, - d4-------— gz)} ф + cos (a+ 9) 2 cos (a+ 9) cos (a+ 9)

, 2 cos 9 ,(T ’/T ’ T T T cos2 9 (T’ sin 9 ,(T ’1 T T ’ cos2 9

+{cos a ig,(d. + d, + d,-d g,)-sin2a ig,( d,-dg

¹ cos( a + 9 ) ^{1 2 3 4} cos ² ( a + 9 )cos( a + 9) ^S ^z ^V2 ^{3 4} cos ² ( a + 9 )

, ■ . cos9 .TT’Д’ T cos2 9

+ sin2a---------- ig, ( d. - d.-----------g ,)} w ;

cos( a + 9 ) ^{1 4} cos ² ( a + 9 )

- . 1 ■ . / L ’ / L’.(L \ cos2 9 (L2.( L ’ sin2 9 (L2, . 2 2Z1( L’.(L ’cos 9 sin 9 (L’,

CT zx = bsin2a[ d2 - (d3 + d4) gz + d4 gz] - (1-2sin a)(;: d3 + d4

2 cos ( a+ 9 ) cos ( a+ 9 ) 2 cos ( a+ 9 )

. r 1 cos 9 v( T ’/ T ’ (T ’cos2 9-sin2 9 (T2. „ . 2 x sin 9 v1( T ’ (T ’ cos2 9

+ {■ sin2a---------- i ( d., + d, - d g ,) + (1 - 2sin a )---------- i ( d, - d.-----------g ,)} w ;

2 cos( a + 9 ) ^{2 3 4} cos ² ( a + 9 ) ^z cos( a + 9 ) 2 ^{3 4} cos ² ( a + 9 ) ^z

Таким образом, компоненты перемещений и напряжений, входящие в граничные условия (система координат z , x связана с границей), определяются соотношениями (16)-(18), где проекции волнового вектора g в системах координат z , X и x J , x K связаны соотношениями (15).

Используемые в [5] матрицы C , характеризующие волновые свойства слоев [9-10], и которые являются основными элементами при построении конкретных решений граничных задач в слоистых конструкциях в данном случае, когда оси z , x образуют с компонентами репера e ^J , e ^K угол a , имеют вид:

где

(

C —

, _ I ^c 11

■(1)

V ^c 21

( c ^c 31

(3) =

V c 41

C — Г⁽¹⁾

V c (3)

Г. „ I ( —г..

c 12 c 11

I C (2) = c22 J V c21

c 32 c 31

I C (4) = c 42 J V c41

c 12

^- c 22

^- c 32 c 42

gx = g

( L ) ( L ) ^C11 = ig z ⁽ ^D1 ⁺

( T )

C 1

c (2) I

I ,

c (4) J

e ig z z

( T ) ( L )

r x ;

( T )

e ig z

cos 9 cos a ( L ) cos( a + 9 ) ² ;

( T )

^C 12 = g z ⁽ - ^C0S ⁹ ^D1 ⁺

e '

( L )

gz z

( T ) e - ^ig z ^z

ig x e ‘ ;

cos a )_;cos( a + 9 )

⁽ ^L ) cos 9 sin a ^L ⁾ ( L\ sin 9 cos a

C2i = igz [---------(D + D2) +--------- cos(a + 9) cos(a + 9)

⁽ ^T ) sin( a + 9 )cos 9 ⁽Д ) sin a

—--/ / -I--

( L )

D J;

1 ⁺ ] ^;

cos( a + 9 ) cos( a + 9 )

( L ) ( L ) ( L ) ( L ) C ₃₁ = cos ² a [ d ₁ + d ₂ - ( d ₃ + d ₄)

cos ² 9

( L )

cos ² ( a + 9 )

₂ 1 ( ^L ) ( ^L )

g_z ] + sin2 a (— d ₃ + d ₄)

cos 9 sin 9 ⁽ ^L 2 . ₂ /L ^{) (}/

----, m g z ^{+ +} sin ^a ⁽ d 1 - d 4 cos ( a+ 9 )

( L )

sin ² 9 ⁽ ^L 2 )

cos ² ( a + 9 ) g z

C ₃₂ = cos ² a

cos 9 ,(T ’(T ’ T T T cos2 9 (T) sin 9 ,(T MT (T) cos2 9

ig, (a, + d + d - d g,) - sin 2a ig, ( d - dg cos(a + 9) 1 2 3 4 cos2(a + 9)cos(a + 9) SzV2 3 4 cos2(a + 9)

. 2 cos 9 ,(T>

+ sin a----------ig,(d1 -d4---- cos(a + 9) 4 cos2 (a + 9)

1 • . / L) z( L(L’ cos2 9 (L2.( L) sin2 9 (L2, . 2 .z1( L(Lcos 9 sin 9

C41 =

-^sin2^a^[^d2^-⁽^d3 + ^d4) gz + ^d4 gz^]-⁽¹^-^2sin^a⁾⁽-^d3 + ^d4

2 cos (a+ 9) cos (a+ 9) 2 cos (a+ 9)

1 cos 9 (T) (T) (T) cos2 9- sin2 9 (Tsin 9 1 (T) (T) cos2 9

C — sin2a----------1(d2 + d3-d g,) +(1 -2sin a)----------1( d3-d.-----------g,).(21)

⁴² 2 cos(a + 9) ^V^{2 3 4}cos²(a + 9) cos(a + 9) 2 ^{3 4}cos²(a + 9)¹ ’

В случае, когда a — 0 элементы (21) матрицы C совпадают с соответствующими элементами этой матрицы для случая совпадения нормали к границе и направления оси симметрии материала, кото- п рые представлены формулами (3.82) в [5]. Если a — — , то получается случай, когда ось симметрии материала касательна к поверхности границы и формулы (21) совпадают с выражениями (3.89)-(3.91) в [5].

Зная выражения для матриц C, можно построить решения различных задач, используя научнометодический аппарат, описанный в [5].

Выводы. Предлагаемый научно-методический аппарат успешно использован при определении напряженно-деформированного состояния в слоистых конструкциях, выполненных из трансверсальноизотропных материалов, и при анализе результатов диагностики состояния плоскослоистых и слоистых цилиндрических конструкций, находящихся в эксплуатации.

Механика

1. Тарнопольский, Ю. М. Пространственно-армированные композиционные материалы /
Ю. М. Тарнопольский, И. Г. Жигун, В. А. Поляков. — Москва : Машиностроение. — 1987. — 224 с.
2. Справочник по композиционным материалам. Кн.1 / Под ред. Б. Э. Геллера. — Москва : Машиностроение. — 1988. — 448 с.
3. Васильев, В. В. Композиционные материалы. Справочник / В. В. Васильев, В. Д. Протасов, В. В. Болотин и др. — Москва : Машиностроение. — 1990. — 512 с.
4. Сизов, В. П. О скаляризации динамических упругих полей в трансверсально-изотропных средах / В. П. Сизов // Известия РАН. Механика твердого тела. — 1988. — № 5. — С. 55–58.
5. Сизов, В. П. Возбуждение упругих волн в слоистых анизотропных конструкциях. Монография / В. П. Сизов, И. П. Мирошниченко. — Saarbrucken : LAP LAMBERT Academic Publishing. — 2012. — 270 с.
6. Сиротин, Ю. И. Основы кристаллофизики / Ю. И. Сиротин, М. П. Шаскольская. — Москва : Наука. — 1979. — 640 с.
7. Федоров, Ф. И. Теория упругих волн в кристаллах / Ф. И. Федоров. — Москва : Наука. — 1965. — 386 с.
8. Корн, Г. Справочник по математике для научных работников и инженеров / Г. Корн, Т. Корн. — Москва : Наука. — 1968. — 720 с.
9. Бреховских, Л. М. Волны в слоистых средах / Л. М. Бреховских. — Москва : АН СССР. — 1957. — 502 с.
10. Виноградова, М. Б. Теория волн / М. Б. Виноградова, О. В. Руденко, А. П. Сухоруков. — Москва : Наука. — 1979. — 384 с.

Список литературы Обобщенный метод скаляризации динамических упругих полей в трансверсально-изотропных средах и его новые применения

Тарнопольский, Ю. М. Пространственно-армированные композиционные материалы/Ю. М. Тарнопольский, И. Г. Жигун, В. А. Поляков. -Москва: Машиностроение. -1987. -224 с.
Справочник по композиционным материалам. Кн.1/Под ред. Б. Э. Геллера. -Москва: Машиностроение. -1988. -448 с.
Васильев, В. В. Композиционные материалы. Справочник/В. В. Васильев, В. Д. Протасов, В. В. Болотин и др. -Москва: Машиностроение. -1990. -512 с.
Сизов, В. П. О скаляризации динамических упругих полей в трансверсально -изотропных средах/В. П. Сизов//Известия РАН. Механика твердого тела. -1988. -№ 5. -С. 55-58.
Сизов, В. П. Возбуждение упругих волн в слоистых анизотропных конструкциях. Монография/В. П. Сизов, И. П. Мирошниченко. -Saarbrucken: LAP LAMBERT Academic Publishing. -2012. -270с.
Сиротин, Ю. И. Основы кристаллофизики/Ю. И. Сиротин, М. П. Шаскольская. -Москва: Наука. -1979. -640 с.
Федоров, Ф. И. Теория упругих волн в кристаллах/Ф. И. Федоров. -Москва: Наука. -1965. -386 с.
Корн, Г. Справочник по математике для научных работн иков и инженеров/Г. Корн, Т. Корн. -Москва: Наука. -1968. -720 с.
Бреховских, Л. М. Волны в слоистых средах/Л. М. Бреховских. -Москва: АН СССР. -1957. -502 с.
Виноградова, М. Б. Теория волн/М. Б. Виноградова, О. В. Руденко, А. П. Сухоруков. -Москва: Наука. -1979. -384 с.

Еще