Обобщенный (результирующий) пространственный вектор плоской трехфазной линейно независимой системы сигналов

В электротехнике трехфазную систему сигналов принято рассматривать в плоской системе координат, характеризуемой тремя сдвинутыми на плоскости под углом 120 ° (2п/3) осями a, b, c . При математическом описании и анализе процессов в многофазных электрических, электромагнитных и электромеханических системах широкое распространение получило понятие обобщенного (результирующего) вектора многофазной системы сигналов. При этом мгновенные значения фазных величин рассматриваются как проекции этого вектора на оси плоской системы координат [1].

Из математики известно, что положение вектора на плоскости определяется его двумя координатами, например декартовыми. Трехфазная система координат может характеризовать положение вектора на плоскости только в том случае, если фазные величины линейно зависимы, т. е. когда выполняется условие

ua + ub + uc = 0,

и, следовательно, одна величина однозначно определяется значениями двух других. Именно такой подход к рассмотрению понятия обобщенного вектора получил в настоящее время наибольшее распространение в технической литературе, когда авторы либо изначально считают переменные трехфазной системы линейно зависимыми, либо искусственно обеспечивают эту зависимость (например, отсутствием нулевого провода, установкой специальных регуляторов и т. д.).

В общем случае в линейно независимой трехфазной системе сигналов результирующий вектор необходимо изначально рассматривать как вектор, опре- деляемый тремя независимыми координатами, т. е. как вектор трехмерного пространства.

Такой подход предложен в [2], где обобщенный вектор характеризуется проекциями на оси пространственной (трехмерной) декартовой системы координат, равными мгновенным значениям соответствующих фазных величин, что предполагает отказ от плоских трехфазных систем координат в пользу трехмерных декартовых. Это обеспечивает математически строгое описание и анализ процессов в многофазных цепях на основе понятия результирующих векторов. Однако при этом подходе теряется связь с традиционно принятыми в электротехнике плоскими координатными системами, имеющими весьма прозрачную физическую интерпретацию, согласно которой оси трехфазной плоской координатной системы – это проекции магнитных осей обмоток трехфазных индукционных источников и потребителей электрической энергии на плоскость их поперечного сечения.

В данной статье предлагается совместить эти два подхода, введя в соответствие плоской трехфазной системе сигналов u_a , u_b , u_c (рис. 1) некоторый пространственный вектор U , характеризуемый координатами u _a 1 , u _{₽ |}, u _у 1 (рис. 2).

Для того чтобы вектор U однозначно определял трехфазную систему сигналов и наоборот, необходимо задать взаимное расположение плоскости трехфазных сигналов и осей трехмерной координатной системы и в результате установить аналитическую связь между мгновенными значениями трехфазной системы сигналов и координатами этого вектора.

u а = u a sin Ф 1 = ^3 u a ,

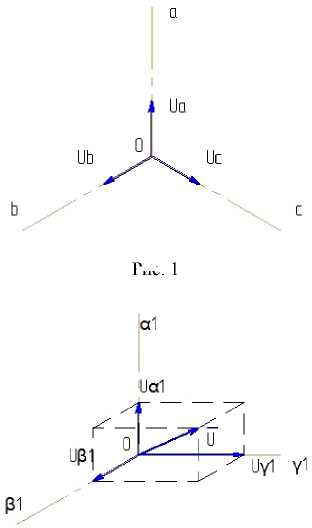
Рис. 1

u р = u b Sin ф ₂ = ~^ub ,

u _у = u c Sin ф ₃ = —^u c .

Рис. 2

Совместим начало координат трехмерной системы с точкой О плоскости, а саму плоскость сориентируем в пространстве так, чтобы нормаль к ней из точки О образовала с осями а 1 , Р 1 , у 1 равные углы (рис. 3). При этом направляющие косинусы нормали ON cos φ 1 =

= cos φ 2 = cos φ 3 =   . При таком положении плоско-

сти отображения на нее осей а 1 , Р 1 , у 1 из любой точки, лежащей на нормали ON , дают систему трех смещенных относительно друг друга на угол 120 ° и пересекающихся в точке О осей, т. е. образуют плоскую систему координат a , b , c трехфазных сигналов u_a , u_b , u_c .

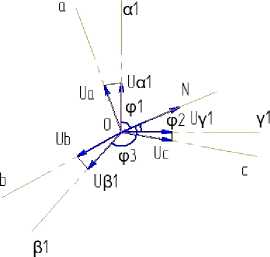
Рис. 3

Считая координаты вектора U проекциями соответствующих фазных величин на оси а 1 , Р 1 , у 1 (см. рис. 3), можно записать:

В векторно-матричной форме уравнения (1) имеют вид

U =

u Y

= ² E 3

ua ub

uc

,

где u _а 1 , u _{P 1}, u _Y 1 - координаты обобщенного вектора u ; u_a , u_b , u_c – мгновенные значения фазных величин;

– множитель, определяемый соотношением

sin ф , = 1 - - cos² ф , ,

i = 1, 2, 3; E =

– еди-

ничная квадратная матрица, каждая строка которой – это координаты единичных направляющих векторов осей а 1 , P 1 , у 1 трехмерного пространства.

Уравнения (1), (2) и рис. 3 наглядно показывают физическую сущность представления трехфазной плоской системы сигналов обобщенным (результирующим) пространственным вектором. Однако на практике удобнее пользоваться пространственными координатными системами, оси которых ориентированы определенным образом относительно магнитных и геометрических осей индукционных источников и потребителей энергии. Поэтому в качестве базовой целесообразно рассматривать координатную систему а , Р , у , ось а которой совмещена с осью фазы а , а ось у - с нормалью ON . Тогда ось Р будет расположена в плоскости трехфазной системы сигналов под углом π/2 относительно оси α по направлению порядка чередования фаз (рис. 4). Таким образом, оси а , Р будут

расположены в плоскости поперечного сечения, т. е. в плоскости магнитных осей индукционных преобразователей энергии, а ось у - вдоль оси вала их ротора.

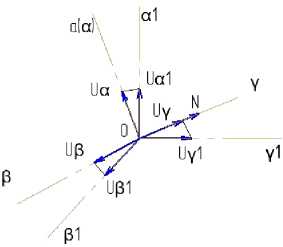
Рис. 4

Путем несложных геометрических построений можно доказать, что координаты вектора U в системе а, в, у связаны с координатами этого вектора в системе аi, вi, уi соотношениями

Нп =---ип--j=U| а 3  а1   J6

u y i ,

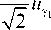
u в

0 +—^ U|

u Y = Vs u a i ⁺ V3 u в 1 - V3 u Y 1

В векторно-матричной форме это преобразование имеет вид

где A1 – матрица координатного преобразования вектора u из исходной в новую трехмерную систему ко- ординат:

	2	1	1
	3	6 1	6 - 1
A 1 =	0	2	2
	1	1	1
	3	3	3

Подставив уравнения (1) в уравнения (3), получим формулы прямого вычисления координат вектора U в системе а , в , у непосредственно по значениям трехфазных сигналов:

211 uа = 3 ua - 3 ub - 3 uc , uв = 0 ■ ua + "Ju ub - "Ju uc ,           (6)

U, =----u„ +--uh +--U, у 3 a 3 b 3 c или в векторно-матричной форме:

U ( а,в,у ) = A

ua ub uc

,

где A – матрица прямого координатного преобразования системы трехфазных сигналов в проекции результирующего вектора на оси декартовой трехмерной системы координат а, в , у :

A = 0

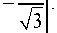
Описание процессов в индукционных преобразователях энергии для случая линейно зависимой трехфазной системы сигналов достаточно часто выполняют в полярных координатах, где результирующий вектор характеризуется модулем U и углом его сдвига φ относительно полярной оси в плоскости поперечного сечения машины.

Применительно к системе линейно независимых трехфазных сигналов необходимо вести речь о цилиндрической системе координат, которая, так же как и декартова трехмерная система, хорошо вписывается в геометрию трехфазных индукционных преобразователей энергии. В этом случае результирующий вектор характеризуется полярными координатами: модулем | Uав | и углом сдвига ф относительно полярной оси проекции Uав вектора U на плоскость поперечного сечения электрической машины и его проекцией иу на ось у, перпендикулярную этой плоскости.

Переход от декартовых координат к цилиндрическим и наоборот при совмещении полярной оси с осью фазы a можно осуществить по формулам

| Uав |= Vuа+ u2, u ф = arctg , и в u у = u у .

Эти формулы позволяют записать связи цилиндрических координат результирующего вектора непосредственно с мгновенными значениями трехфазных сигналов:

|U ав | = I V ^и 2 + u b ^{+ u} 2 ^- u a u b ^- u a u c - u b u c ^,

1 Uu - и I

Ф = arctgV31 -— b---c — I,          (9)

( 2 u a ^- u b ^- u c J

2 u у =     ( u a ⁺ u b ⁺ u c ) .

Отметим, что уравнения (6), (7), (8) полностью совпадают с уравнениями, приведенными в [2], однако они получены с использованием плоской трехфазной системы координат. Кроме того, здесь, в отличие от [1; 2], не пришлось искусственно вводить масштабирующий множитель 2/3. Он автоматически появляется в результате геометрических построений.

Из сравнения третьих уравнений (6) и (9) также следует, что координата иу вектора и не зависит от вида используемой системы координат. Она не изменится и не отразится в других координатах вектора U, если координатным системам придать вращение вокруг оси у. Кроме того, эта координата не участвует в электромеханическом преобразовании энергии. По- этому при анализе переходных процессов в электромеханических системах с учетом электромагнитных явлений эта составляющая, согласно [2], может рассматриваться отдельно либо, если в этом нет необходимости, не рассматриваться вовсе.

Представленные выше геометрические построения преобразуют плоскую линейно независимую трехфазную систему сигналов в две подсистемы линейно зависимых сигналов.

Первая подсистема одномерная и с учетом третьего уравнения системы (6) определяется сигналом u _Y , пропорциональным, согласно терминологии, принятой в электротехнике [3], составляющей нулевой по-1 следовательности и = —^= и ₀.

' V2

Вторая подсистема двухмерная и задается координатами и _а и и _р , которые характеризуют трехфазную систему сигналов ненулевой последовательности u_{a 1}, u_{b 1}, u_{c 1}. Эти сигналы могут быть определены по первым двум уравнениям системы (6) после замены в них переменных u_a , u_b , u_c на u_{a 1}, u_{b 1}, u_{c 1} с учетом условия и + U- + и = 0.

a ₁ b ₁ c ₁

Таким образом, проекцию Uар обобщенного (результирующего) вектора U на плоскость поперечного сечения электрической машины правильнее называть обобщенным (результирующим) вектором составляющих ненулевой последовательности трехфазной системы сигналов. Это понятие совпадает с общим понятием «результирующий вектор трехфазной системы сигналов» только в частном случае, когда и 7 = 72и 0 = 0.

В заключение сделаем следующие выводы:

– предложенный в данной статье подход позволил распространить понятие обобщенного (результирующего) вектора на трехфазную плоскую линейно независимую систему сигналов, что в свою очередь позволяет при описании процессов в таких трехфазных цепях использовать компактные векторно-матричные представления;

– при выводе уравнений, связывающих координаты обобщенного вектора с мгновенными значениями трехфазных сигналов, отпадает необходимость искусственного введения масштабирующего множителя 2/3, согласующего модуль результирующего вектора с амплитудными значениями фазных величин. Этот множитель автоматически появляется в результате геометрических построений;

– описание процессов с помощью пространственных результирующих векторов возможно не только в трехмерной декартовой системе координат, но и в цилиндрической системе координат, благодаря чему получены уравнения, связывающие цилиндрические координаты вектора с мгновенными значениями трехфазной линейно-независимой системы сигналов.