Обобщённая линза: анализ осевого и поперечного распределения

Под аксиконом [1] понимается любой оптический элемент, обладающий осевой симметрией, который за счёт отражения и/или преломления преобразует свет от точечного источника, расположенного на оптической оси, в осевой отрезок. В этом состоит отличие аксикона от линзы, которая изображает точечный источник в точку, и его преимущество. К сожалению, это преимущество аксикона сопровождается низким качеством изображения при использовании его как отдельного изображающего элемента [2, 3]. Другое преимущество аксикона – изображение точки с меньшим поперечным дифракционным пределом (меньшим расплыванием) [4] – имеет своим продолжением в качестве недостатка более высокий уровень боковых лепестков, что также препятствует получению качественного изображения.

В работе [5] было показано, что при использовании средств дифракционной оптики тандем «линза + аксикон» можно заменить одним дифракционным элементом (названным фраксиконом), фаза которого имеет дробную степенную зависимость от радиальной координаты. В этой же работе было показано, что за счёт вариации параметров можно получить не только аналог линзакона [6], но и логарифмического аксикона [7], но без сингулярности в центральной части оптического элемента. Дифракционное исследование аксикона в сходящемся сферическом пучке было проведено в работах [8, 9].

Рефракционные аналоги таких элементов исследовались в работе [10] в рамках геометрооптической модели. Оптический элемент назван обобщённой линзой, так как при конкретных параметрах он сводится к классическим элементам, таким как параболическая линза или аксикон. Однако вариации параметров позволяют получать в одном элементе комбинированные свойства набора из двух и более оптических элементов.

Исследование фокусирующих свойств обобщённой линзы по сравнению с классическими оптиче- скими элементами является актуальным для многих приложений, так как позволит заменить набор оптических элементов одним дифракционным элементом.

В данной работе на основе метода стационарной фазы получены аналитические выражения для осевого распределения, формируемого обобщённой линзой в параксиальном приближении. Два типа аналитических выражений обеспечивают высокую точность расчёта в различных диапазонах значений степени обобщённой линзы.

На основе классического метода стационарной фазы выполнен анализ поперечного распределения, который показал возможность формирования с помощью обобщённой линзы более узкого светового пучка, чем обеспечивает линейный аксикон с той же числовой апертурой.

1. Анализ осевого распределения

Рассмотрим радиально-симметричный дифракционный оптический элемент, фаза которого имеет произвольную степенную зависимость от радиальной координаты. Комплексная функция пропускания фазового элемента имеет следующий вид:

т ( r ) = exp [- i ( k о, r ) ^Y] , r <  R , (1) где k = 2 n / % , % - длина волны, у - положительное действительное число, а ₀ - безразмерный коэффициент, связанный с числовой апертурой оптического элемента и определяющий максимальный угол наклона лучей к оптической оси.

Дифракция плоской волны на оптическом элементе (1) в параксиальном случае вычисляется по формуле:

U ( Р , z ) = ^{— ex}P iz

ч    i— Р 2

ikz + —— х 2 z

R xjт(r)exp ikr2

2 z

J ₀

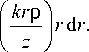
На оптической оси формула (2) примет вид:

k

U (p = 0, z) = — exp( ikz) x

R

. 2

R               v ikr2    , xj exp - i (к a r) + — r dr.

Для вычисления интеграла в формуле (3) воспользуемся методом стационарной фазы (МСФ) [11]. Этот метод основан на том, что при быстроосциллирую-щей подынтегральной функции главный вклад дают окрестности точек, в которых частота (производная от фазы) равна нулю. Поэтому выполним разложение фазовой функции в (3) в ряд Тейлора и запишем приближённое равенство:

^exp^[ f ^{( r )]} = ^exp { i [ f ( ^r 0 ) ⁺ f ' ( ^r 0 )( ^{r - r} 0 ) ² /² ] } , ⁽⁴⁾

в котором точка r ₀ определяется из условия: f ‘ ( r ) = 0.

Если стационарных точек несколько, то производится разбиение отрезка интегрирования.

В классическом МСФ остальные множители в подынтегральной функции заменяются значениями при подстановке r = r ₀, а пределы интегрирования расширяются до бесконечных. Естественно, предполагается, что стационарная точка лежит внутри отрезка интегрирования и не очень близко к его концу. Если она совпадает с концом отрезка, то соответствующий ей предел интегрирования заменяется нулём (а не бесконечностью).

В работах [8, 12] использовалось уточнение МСФ, состоящее в сохранении конечных пределов, однако подстановка r = r 0 выполнялась в соответствии с классическим МСФ.

В данной работе мы и сохраняем конечные пределы интегрирования, и не делаем подстановки r = r 0 . Будем называть это модифицированным МСФ.

В первом подходе произведём следующее преобразование показателя в (3):

f(r) = -(ka0r)" + ikrz" = -P(rY - ar2 ),

где Р = ( к a ₀ ) ^у , a =

к ^у

2 z a 0

.

Таким образом, подлежащий вычислению интеграл записывается в виде:

U ' ( z ) = -— exp( ikz ) x

z

R xj exp [-ip( rу

ar ² ) J r d r .

Так как при у = 1 и у = 2 функция фазы в (7) уже является квадратичной, то в результате применения модифицированного МСФ получим точные решения, рассмотренные в [13, 14]. Поэтому далее рассматриваем эти значения как границы исследуемых диапазонов значений: 0 < у <  1, 1 < у <  2, у >  2 . Заметим, что решение для у = 2 нельзя получить непрерывным переходом из решений для соседних диапазонов.

В первом подходе надо проанализировать функцию (6). В этом случае имеем одну (при 0 < у < 1) или две стационарные точки:

r₁ = 0; r ₂ =

2 а |^{у- 2} у ^J

При наличии двух стационарных точек (при у >  1) точка перегиба:

r p

Г 2 а ) У- ²

I У ( У- 1) J

Значения в стационарных точках: f ( r 1 ) = 0,

. Г 2       2 а ) у ^{- 2}

f(r,) = а\1 II I , IУ Л У )

„ I - 2 а , у >  2, f ( r ) =^            ;

[+~ , 1 <у< 2,

f '( r 2 ) = 2 а ( у- 2).

Рассмотрим ещё один подход к вычислению интеграла в формуле (3). Сделаем замену переменной x = ( к a ₀ r )² и после некоторых преобразований получим:

U¹¹ ( z ) = - ib exp ( ikz ) x

( ^k a ^R )²                                                         (11)

x j exp [-i (xу/2 - bx)Jdx, где b = 1/ (2kza0).

В этом случае под интегралом имеется только экспонента, и модификация МСФ будет состоять только в конечности пределов интегрирования. Ниже будет по казано, что в зависимости от значения у преимущества имеет либо первый подход (7), либо второй (11).

Показатель в (11) имеет одинаковые свойства при всех значениях у, кроме у = 2 . Имеется одна стацио- нарная точка:

x 0

2 b ] у ^{- 2} у^J

Точка перегиба отсутствует. Значения в стационарной точке:

f(x0) = -bx0(у 2) у

f '( x 0 ) =

b ( у- 2)

^{2 x} 0

Сравнивая (7) и (11), можно доказать, что при использовании классического МСФ получится одинаковый результат в обоих подходах.

Заметим, что второй подход (11) позволяет получить точное решение при у = 4 [15]:

U " ( z ) =

-

i exp ( ikz ) _x 2 a 0 kz

x exp

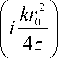
T 2

j exp( - it ²)d t ,

T

где T = ^- ГТ ' r 0 , T 2 = 4 z

R ²

^^^^^^s

r 0 ²

r ₀

Интеграл в (14) выражается через функции Френеля. Далее в тексте мы будем приводить выражения в форме, аналогичной (14), сохраняя знак интеграла, так как явное выражение через функции Френеля зависит от знаков нижнего и верхнего пределов.

Далее рассмотрим разные диапазоны параметра у .

2. Аналитические и численные оценки осевого распределения для различных диапазонов параметра у

2.1. Диапазон 0 <  у < 1

В этом диапазоне сравнение вычислений с помощью первого и второго подходов наиболее просто и наглядно, так как в обоих вариантах имеется только

одна стационарная точка.

При использовании выражения (7) получаем:

U I ( z ) = exp ( ikz ) exp [- i в f ( - 0 ) ] x

I 1 x exp

IY-2 P

--exp

Y-2 P

i 2

7(2-7)

где

T =- - о

-

- ^( R - - 0)’

2 z

ikka-Y) r 2

2 z ⁰

Y2-7

-

⁷                '■ T             .

a 0 ⁷ ( kz ) ’(’-у) J exp( it ²)d t • ,

I k (2 -y )

2 z

T ’ = ( R - - 0 )

I k (2 -y ) 2 z

При y = 1 выражение (15) позволяет получить точное решение.

Использование второго подхода (14) приводит к следующему выражению:

U¹¹ ( z ) = - exp( ikz )exp [ - i в f ( r ₀) ] x

x

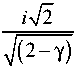
¹        7             у T 2

Y ^{2 -7} « 0 ^-Y ( kz ) ^{2(2 -} y ) J exp( it ²)d t , T 1

где

k^ _R

1        ^- 0A       о , ’

8 z

-

r ₀

- 2 I k (2 -у )

8 z

Из сравнения формул (15) и (16) видно, что множитель перед интегралом в обеих формулах одинаковый, откуда становится очевидным совпадение «ли-

нии узлов» на графиках интенсивности (рис. 1), хотя сам характер осцилляций заметно отличается.

Для получения численных оценок был выполнен расчёт по формуле (3) численным интегрированием. Параметры расчёта: % =1 мкм, R = 1 мм, у =0,5. а ₀ определялось из условия, что числовая апертура на краю элемента равна заданному значению п :

NA ( R ) = а^уу ( kR ) ^7- 1 = п . (17)

Положив ( п =0,1), мы обеспечиваем условие параксиального распространения для периферийных лучей. При заданных выше параметрах из (17) получается а ₀ = 251,3.

Сравнение с результатом численного интегрирования выражения (3) показывает (рис. 1), что в данном диапазоне формула (15) является более точной (погрешность менее 7%), чем (16) (погрешность 11%).

Как видно из рис. 1, распределение интенсивности вдоль оптической оси имеет довольно равномерный характер. Таким образом, обобщённая линза при у < 1, соответствующая в этом случае фраксикону [5], позволяет формировать распределение, аналогичное логарифмическому аксикону [7]. При этом фраксикон не имеет особенности в центральной части и не требует экранирования.

Зависимость средней линии интенсивности от расстояния при 0 < у <  1 можно приблизительно описать функцией (до области тени):

Y

I ( z ) - ( kz ) (2-7) . (18)

Это выражение легко получается при использовании классического МСФ.

Из (18) очевидно, что при у^ 1 получается линейный рост интенсивности, а при у ^ 0 средняя линия интенсивности будет постоянна. Однако последний случай означает отсутствие какого-либо элемента и соответствует дифракции на круглом отверстии, которая характеризуется высоким контрастом осцилляций интенсивности. Поэтому наиболее интересными являются «средние» значения у . В частности, для у = 0,5 средняя линия интенсивности довольно медленно меняется I ( z ) - ( kz ) 13 при небольших осцилляциях интенсивности (см. рис. 1).

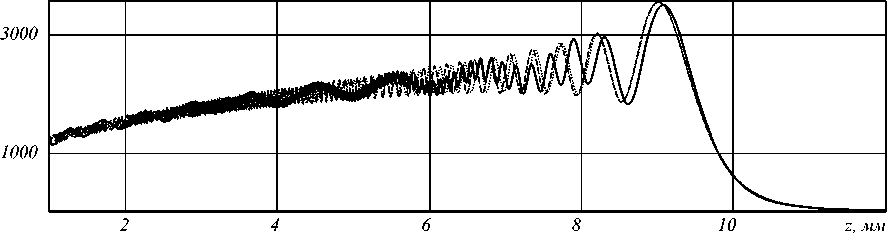
Рис. 1. График интенсивности вдоль оптической оси при у = 0,5: по формуле (15) (точечная линия), по формуле (16) (сплошная линия), численным интегрированием (3) (пунктирная линия)

2.2. Диапазон 1 <  Y 2

Первый способ вычислений в данном диапазоне был подробно рассмотрен в [14], поэтому приведём финальный ответ для случая R >  r p (это условие на

рушается лишь на участке дальше максимума интенсивности, где она уже мала):

U ( z ) =

exp ( ikz )

Ц

|    Ц — 2

exp - i   r„

I 2 z p

-

T 2 = ( R - Ш — (2 -Y ). У 2 z

При R <  r p остаётся только первое немного изменённое слагаемое:

U ( z ) =

к^{1 7} exp ( ikz )

2 z а 0 ц‘ R ^{7- 2} - к ' ^Х

x

+ eXP( ikz) exp [-iaf (r)] x Y-2

x I exp - i ^k(Y- ²⁾ ( R - г ,)²

exp ( - i ц‘ ( k a ₀ R ) ⁷ ) exp | i—R ² |- 1

- exp

- i

к ( Y- 2) 2 z

^{( r} 0

-

r p ^{) 2}

-

i 42 7(2-7)

exp ( ikz ) exp [- i a f ( r ₀ ) ] x

1       7             у T> xy2-7 a2-Y (kz)2(2-т) jexp(it2)dt,

T

где ц =

( Y+ 3) 7 ( 7- 1)

-

1, T 1 = - ( r - Г р ) — (2 -Y ) 2 z

где ц' = 5/ ( y+ 3 ) .

При y =1 формула (19) становится точной, т.к. r ^ 0, из-за чего первое слагаемое в (19) стремится к ^р 7^1

нулю, а остальные слагаемые дают формулу (15), которая, как уже упоминалось, при 7 = 1 является точной.

При вычислениях вторым способом сохраняет силу формула (16). Результаты вычислений по формулам (16) и (19) показаны на рис. 2. Параметры расчёта такие же, как в предыдущем разделе, за исключением двух параметров: 7 = 1,5, a ₀ = 0,0089 .

Так же, как и в предыдущем диапазоне, сравнение с численным интегрированием показывает, что формула (19) является более точной (погрешность менее 10%), чем (16) (погрешность 16%).

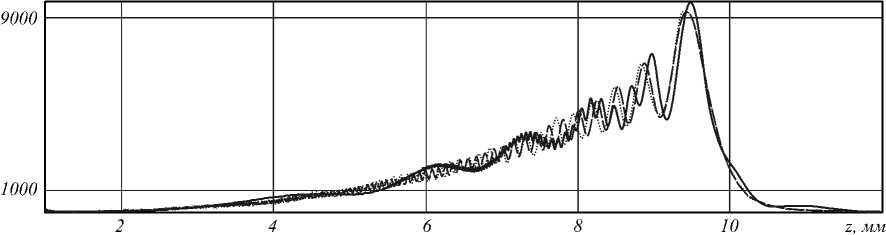
Рис. 2. График интенсивности вдоль оптической оси при у = 1,5: по формуле (19) (точечная линия), по формуле (16) (сплошная линия), численным интегрированием (3) (пунктирная линия)

Как следует из рис. 2, в диапазоне 1 < 7 <  2 характер зависимости интенсивности от расстояния совсем иной, чем при 0 < 7 <  1, но аппроксимруется также функцией (18). В частности, при у = 1,5 средняя линия интенсивности имеет зависимость I ( z ) ~ ( kz )³ (рис. 2).

Заметим, что при 7 <  2 область тени начинается за условной границей:

z s = R / NA , (21) которая при рассматриваемых параметрах равна z s = 10 мм .

В случае параболической линзы у = 2 граница (21) соответствует геометрическому фокусу.

2.3. Диапазон у > 2

В этом диапазоне ситуация существенно иная. Вычисление первым способом, как будет показано ниже, оказалось довольно сложной задачей. Рассуждая ана

логично другим диапазонам, при R >  r_p получаем сле

дующее выражение:

U¹ ( z ) = - exp( ikz )

exp

-

-

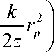
+exp-i 2z) exp [-i ₽f (г) ]x

x <  exp

- exp

+

, k ( 7- 2) i

2 z

( R - r ,)²

-

- i

k ( 7- 2) 2 z

i 42 7(2-7)

^{( r} 0

-

r p ^{) 2}

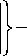
exp( ikz )exp [- i в f ( r ) ] x

1     7          у T xy2-7 a0-7 (kz)2(2-у) jexp(-it2)dt,

T 1

где T = - ( r

-

r p

a k ( Y- 2) )N 2 z

, T 2 = ( R - r o )

I k ( У— 2)

2 z

В случае R <  r_p остаётся только первое слагаемое:

U‘ ( z ) = - exp ( ikz )

exp

-

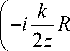
Заметим, что ответ в данном приближении не зависит от у.

К сожалению, результаты численных расчётов показали, что при малом z (в области геометрической тени) формула (22) даёт очень завышенные значения интенсивности. Причина в неполной корректности применения модифицированного МСФ. Сохранение конечных пределов вполне возможно, но без замены r на r o в (22) появляется второе слагаемое, которое не имеет предела при увеличении R и намного больше остальных слагаемых. Это слагаемое является ложным, так как получено при квадратичной аппроксимации вблизи r = r ₀.

В силу вышесказанного возможны два варианта коррекции:

- применить метод стационарной фазы полукласси-ческим способом, ограничиваясь только сохранением конечных пределов, тогда второе слагаемое не появляется;

- это слагаемое оставить, но верхний предел R заменить на такое значение r u , где квадратичная аппроксимация ещё правомерна. Если же взять r u = 2 r ₀- r p , что соответствует симметричному отрезку интегрирования с центром в r _o, то второе слагаемое обратится в нуль.

Действуя по второму варианту, интеграл по отрезку [ r u , R ] положим равным нулю (это оправдано как идеей классического МСФ, так и численными исследованиями).

Первое слагаемое в (22) также следует несколько скорректировать в соответствии с рассуждениями, подробно описанными в работе [14].

Таким образом, после поправок при R <  r u (22) принимает следующий вид:

U * ( z )

exp ( ikz )

Ц

exp

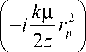
+ ^ex p - i 2 z ) exp ^[ i p f ( r o ) ]^x

X/exp - ik(Y 2) (R - ro )2 -

L l 2 z _]

. k ( у- 2)/       \² ]

^- exp L^- i   v    ( r o - r p ) ]-

—/== exp^{( ikz} ) ^exp ^[- i P f ( r o ) ] ^x

V(2-Y)

¹ Y            у T 2

xy ^{2 -Y} a ^{2 Y} ( kz ) ²⁽² у J exp( - it ²)d t ,

T

io

( Y+ 3) Y ( Y- 1)

T 2 = ( R - r od k^

V 2 z

^T 1 = ^{- ( r} o ^- r p )

I k ( Y- 2) 2 z

При R >  r_u (22) принимает следующий вид:

U ( z )

exp ( ikz )

Ц

i

7(М

( Л Ц 2 exp - i—r„

( 2 z ^p

exp( ikz )exp ^[ - i в f ( г ) ] x

1 y Y T x2y2-Y a2 Y (kz)2(2-у) Jexp(-it2)dt, o

т ( з k ( у- 2)

где T = ⁽ r o ^- r p      2 z   ,

Если результат находится по формуле (23), то де лается аналогичная коррекция. При R < rp :

U ( z )

a exp ( ikz ) Ц R ^{Y- 2} - a

x exp ( - i [W R ^Y ) exp ^ i2-R ²

-

1 ,

где u/ = 5/(у+ 3), a =---1—r.

'⁽       ) ’      2 a^ zk ^{Y- 1}

Эта формула совпадает с аналогичной в диапазоне 1 < у< 2.

При вычислениях вторым способом получаем следующий результат:

U " ( z ) =

i Л Vy^{3 2}

exp( ikz )exp ^[ - i в f ( r, ) ] x

1 Y             у T> xy2-Y a,2 Y (kz)2(2 y> Jexp(-it2)dt,

T 1

k ( Y- 2) _T _ R² - r o ² I k ( y- 2) , T .

8 z r _o V 8 z

При у = 4 формула (27) становится точной. Результаты вычислений по формулам (24)-(27) показаны на рис. 3. Чтобы имело смысл сравнение с квадратурной формулой, выбрано у =3, когда (27) не является точной. Из (17) параметр a _o = 9,46 -Ю ^{- 4}.

Сравнение с результатом численного интегрирования показывает, что формула (27) является более точной (погрешность менее 13%), чем (24)-(26) (погрешность 15%), что отличает данный диапазон от предшествующих. Также видно, что область тени теперь располагается до границы (21).

Зависимость интенсивности от расстояния такая же, как (18). В частности, при Y = 3 средняя линия интенсивности имеет зависимость * ( z ) ~ ( kz )^-3 (рис. 3).

где T 1 = - r _o

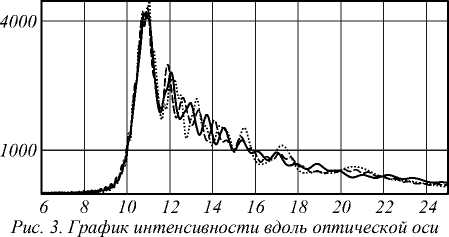
при Y = 3: по формулам (24)-(26) (точечная линия), по формуле (27) (пунктирная линия), численным интегрированием (3) (сплошная линия)

, . 2,4 ( NA ) ^=2 ( z p„ z =

0 k I Y ) IR

Y-1

Y-2

.

При у = 1 размер светового пятна имеет постоян-

ную величину, не зависящую от радиуса оптического

элемента и расстояния:

П = 2,4

^{P o} ’ ^Y =1 k • NA

.

3. Анализ фокального распределения

Выражение (2) можно приблизительно оценить, используя классический МСФ:

U (р, z) = - i exp (ikz) exp [-i вf (r) ] X

Анализ выражения (33) предсказывает уменьшение размера светового пятна при z ^ 0 для у <  1 и

Y >  2 , а для 1 <  y <  2 - при z ^ ^ .

На рис. 4 показаны зависимости радиуса светового пятна (33) от расстояния z при нескольких значе-

2n

X

VlY-2

1              Y

( ya Y ) ^{2 -y} ( kz ) ² ( ^{2 -} y ) J 0

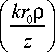
Интенсивность в этом случае имеет следующий вид:

I (р, z) 7/^ (7ао)2-Y (kz)(2-Y) J2 (krr7.

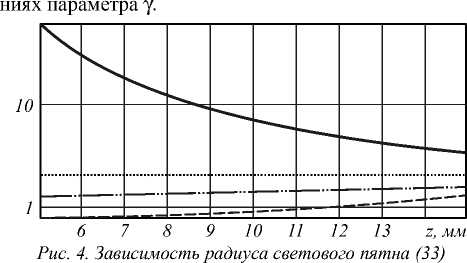
от расстояния при у 0,5 (штрихпунктирная линия), Y =1 (точечная линия), 7=1,5 (сплошная линия), 7=2,5 (пунктирная линия)

Как следует из рассуждений предыдущих разделов, максимальное значение на оптической оси (фокальная область) находится вблизи границы тени (21). Используя выражение (17), можно записать общее выражение максимального (фокального) значения для всех диапазонов у через числовую апертуру NA:

I ( 0, z_s ) "

3^ kR • NA . IY-2|

Из полученной оценки следует, что максимальное значение в фокусе получается при у= 2, т.е., как и следовало ожидать, параболическая линза обеспечивает наилучшую концентрацию энергии в фокальной области. Однако поперечный размер фокального пятна при этом не является минимально возможным. Считается, что аксикон ( у = 1), формирующий бессе-левый пучок [4], обеспечивает наиболее протяжённое и компактное фокальное распределение.

Рассмотрим поперечное распределение, которое формирует обобщённая линза (1). Используя выражение (29), поперечный размер можно оценить по первому нулю функции Бесселя:

Ро (z ) =

2,4 z kr ₀ ,

где r ₀ =

k ' ] Y ^{- 2}

z ао 7

1 у R Y"1 ) Y^ z • NA I

Для удобства анализа перепишем (31) в следующем виде:

Из рис. 4 следует, что при у <  1 и у >  2 обобщённая линза обеспечивает формирование светового пятна меньшего размера, чем аксикон. Причём уменьшение размера наиболее значительно при z ^ 0 для у >  2 , что соответствует области тени и является мало интересным с практической точки зрения резуль-

татом.

Поэтому рассмотрим размер светового пятна в максимуме интенсивности, который достигается вблизи границы области тени (21):

2,4

^р о ⁽ zs ) 1            V(у-2) .

k • NA •у1 (Y )

Из выражения (35) следует, что при у ^{1/( у 2)}> 1 даже в области максимальной интенсивности размер све-

тового пятна может быть меньше, чем формирует ак-сикон (34). На рис. 5 показана зависимость у ^{1/( у -2)}, из

которой наглядно видно, что при у <  1 и у >  2 размер светового пятна (35) будет меньше (34).

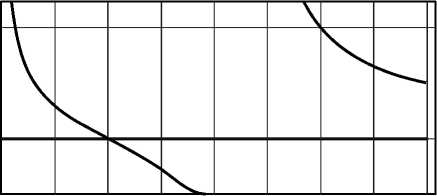
О 0,5    1.0    1.5   2,0   2,5   3.0   3.5 у

Рис. 5. Зависимость функции y *^{,/ Y 2}2 от у

К сожалению, классический МСФ позволяет получить довольно приближённые оценки. На рис. 6 показаны зависимости размера светового пятна по полуспаду интенсивности (FWHM) от расстояния, рассчитанные методом численного интегрирования выражения (2).

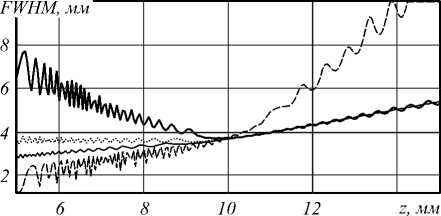
Рис. 6. Зависимость размера светового пятна (FWHM) (33) от расстояния при Y = 0,5 (тонкая сплошная линия),

Y = 1 (точечная линия), Y = 1,5 (сплошная линия),

Y = 2,5 (пунктирная линия)

Как видно из рис. 6, действительно, при γ<1 и γ>2 в области z <  z s обобщённая линза (1) позволяет формировать световое пятно меньшего размера, чем при использовании аксикона. Однако при γ>2 это область тени, поэтому более перспективным является использование параметра γ<1 . Заметим, что в плоскости z = z s численное моделирование показывает одинаковый размер светового пятна для рассмотренных значений у .

На рис. 7 показаны графики поперечного сечения интенсивности в плоскости z = z s /2 для y =0,5 и Y=1.

s

® в®

а)                                        б)                                        в)

Рис. 8. Вид фазы обобщённой линзы (1) при NA = 0,1 и R = 1 мм для y = 0,5 (а); Y = 1 (б) и Y = 1,5 (в)

Заключение

Предложена модификация метода стационарной фазы, на основе которой получены два типа аналитических выражений для осевого распределения комплексной амплитуды, формируемого обобщённой линзой в параксиальном приближении. Каждое из полученных выражений обеспечивает высокую точность расчёта в различных диапазонах значений степени обобщённой линзы у.

Средняя линия интенсивности вне области тени имеет зависимость

Y

I ( z ) ~ ( kz ) (2-Т) .

Границей области тени, которая располагается справа при γ<2 и слева при γ>2, является геометрический фокус параболической линзы (γ=2). Максимальное значение интенсивности для любых значений γ достигается вблизи границы области тени.

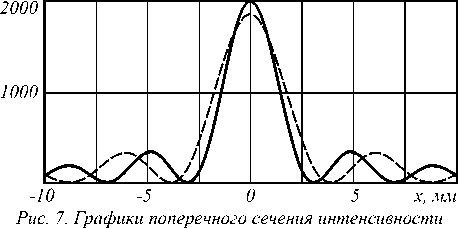
в плоскости z = z s /2 при y 0,5 (сплошная линия), Y = 1 (пунктирная линия)

Как видно из рис. 7, фраксикон (γ=0,5) в этом случае обеспечивает как меньший размер светового пятна, так и большее значение интенсивности, чем аксикон (γ=1).

Объяснить этот эффект можно структурой обобщённой линзы при γ<1. В отличие от обычной линзы, у которой значение числовой апертуры максимально в периферийной области, у фраксикона числовая апертура увеличивается с уменьшением радиуса оптического элемента. На рис. 8 показаны фазы дифракционных оптических элементов, соответствующих (1) при NA =0,1 и R = 1 мм для различных значений параметра γ. Таким образом, если мы согласовываем значения числовой апертуры на краю элементов в периферийной части NA ( R ) в соответствии с (17), то при γ<1 в центральной части элемента будет достигаться более высокое значение числовой апертуры, которое и обеспечивает меньшее значение светового пятна.

При 0< у <1 обобщённая линза соответствует фрак-сикону (дробному аксикону) и позволяет формировать практически равномерное распределение интенсивности. Такое действие аналогично логарифмическому ак-сикону, но при этом фраксикон не имеет особенности в центральной части и не требует экранирования.

При 1< у <2 фраксикон обеспечивает рост интенсивности вдоль оптической оси быстрее линейного (до области тени).

При γ>2 обобщённая линза формирует интенсивность, которая имеет максимальное значение вблизи области тени, и при дальнейшем увеличении расстояния убывает.

В диапазоне γ<2 первый тип аналитических выражений является более точным и позволяет получить точное выражение для γ=1, а при γ>2 более точным является второй тип аналитических выражений, который позволяет получить точное выражение для γ=4.

В диапазоне γ < 1 обобщённая линза позволяет сформировать более узкий световой пучок, чем обеспечивает линейный аксикон с той же числовой апертурой. Это связано с тем, что в этом случае числовая апертура увеличивается от периферии к центру оптического элемента.

Работа выполнена при финансовой поддержке гранта РФФИ 13-07-97004-р_поволжье_а, гранта Президента РФ поддержки ведущих научных школ НШ-4128.2012.9, а также Министерства образования и науки Российской Федерации.