Обобщённая методика исследования информационных свойств каналов и систем распознавания

Исследованию свойств различных дискретных каналов, систем передачи и извлечения информации с позиций теории информации уделяется достаточно большое внимание.

Классическим примером является исследование пропускной способности двоичного симметричного канала передачи информации [1]. При расчёте пропускной способности основным является расчёт среднего количества взаимной (парной) информации.

В [2] среднее количество взаимной (парной) информации использовано в качестве информационного показателя качества функционирования систем распознавания, что позволило осуществлять сравнительный анализ систем, работающих по разнородным признакам и имеющих различные алфавиты распознаваемых классов. На основе такого информационного показателя качества выполнен анализ для частного случая: вероятность правильного распознавания целей различных классов одинакова, канал распознавания симметричный.

Известно, что объединение данных, поступающих от нескольких датчиков, например, объединение данных от нескольких каналов распознавания в комплексной системе, позволяет повысить качество получаемой информации. При этом каждый датчик может иметь своё множество классов [3] – датчики разнородные. Необходимо на основе объединения датчиков принять решение о соответствии наблюдаемого объекта одному из классов заданного алфавита, например: «свой» или «чужой» в комплексной (интегрированной) системе опознавания [4–8].

Цель данной статьи - предложить обобщённую методику использования информационного показателя для оценки качества каналов и систем распознавания, не ограниченных частными случаями, рассмотренными в [1, 2].

Количество взаимной (парной) информации в двоичном несимметричном канале распознавания

Матрица условных вероятностей переходов двоичного канала распознавания представляется в виде

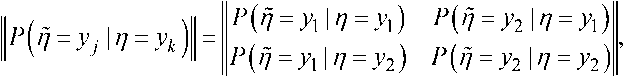
где η – двоичный символ на входе канала, отображающий принадлежность распознаваемого объекта к одному из классов у 1, у ₂ двоичного алфавита, Г] - двоичный символ на выходе канала, отображающий оценку класса распознаваемого объекта.

В отличие от известных методик, в которых двоичный канал предполагается симметричным, рассмотрим несимметричный канал с матрицей переходов

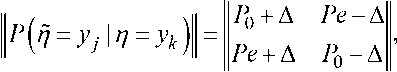
где P о - средняя вероятность правильного распознавания, Pe - средняя вероятность ошибочного распознавания; ∆ – параметр несимметричности канала.

На введённые переменные накладываются ограничения

^О+Рс = 1;

! 0<Р₀+А<1;

0<Ре-А<1;

0<Р0-А<1;

0<Ре + А<1.

Среднее количество взаимной информации рассчитывается по формуле [1, 9]

Цп;п) = н^-н^ , где и       – безусловная и условная энтропии.

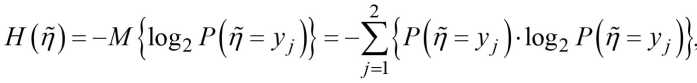
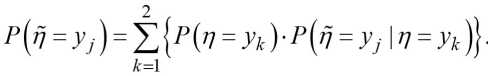
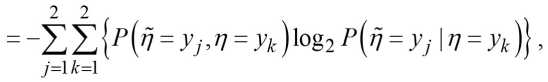
где Р^п = у_рп = У^ = Р^1 = Ук\^р^ = У, I П = У к ).

Выражение для расчета среднего количества взаимной информации имеет вид

+

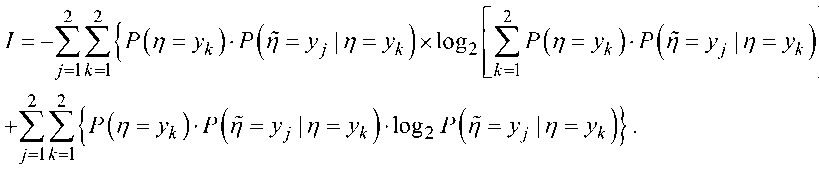
Будем считать, что P(п = у ₁) = P(п = у ₂) = 0,5. Тогда с учётом (2) и (3) выражение (4) запи-

шется в виде

^ = -|](* + 2 А) ■ log2 [РР-] + (1 - 2 Д) ■ log, [-^]] + +|Х^+д)-^ (^+дыл’+дно8, (.?,•+д>+                 (5) Ц№-д).1о82(№-д)+(р0-д)^2(р0-д)}.

Полученное выражение будем анализировать как функцию I (А) с параметрами P ₀ и Pe . Для нахождения возможного экстремума представленной функции найдём её частную производную по ∆.

9А

2 Г °82

1-2А

1 + 2А

+ log2

(Р₀ + А)(Ре + А) (Р₀-А)(Ре-А)

ац ₀„ ф^др^+дХ^+д) ) , 5Д     Ц1 + 2А)²(Р₀-А)(Р_С-А)^

После преобразования полученного уравнения найдем

А-(2-8-РоРс?) = О=> А = 0.

Для рассматриваемой функции I (А) найденная точка А = 0 (симметричный канал) является точкой минимума при заданном значении Pe . Следовательно, симметричный канал менее эффективен - по рассматриваемому информационному показателю I - по сравнению с эквивалентным несимметричным каналом (с таким же значением Pe ).

Проанализируем более подробно двоичный несимметричный канал.

С учётом P ₀ = 1 - Pe выражение (5) принимает вид

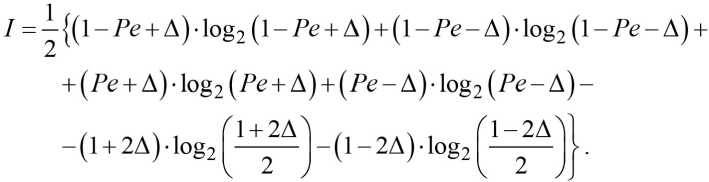
Анализ (6) показывает, что функция I(А) является чётной (I(А) = I(-А)), поэтому будем рассматривать только положительные значения переменой ∆. А так как реально нас интересуют только значения вероятности полной ошибки в интервале

0;-

, то с учётом ограничений

• (3)    рассматриваемый интервал для переменной А примет вид А е [0; Pt?].

Результаты расчётов по (6) представлены в табл. 1.

Анализ табл. 1 позволяет сделать вывод, что при любом фиксированном значении пе- ременной Pe на интервале Pe g 0; —

функция I(∆, Pe) с увеличением ∆ монотонно возрас тает, а при ∆ → 0 принимает свое минимальное значение, которое с ростом Pe уменьшается. Свое максимальное значение (равное 1) функция I(∆, Pe) принимает в точке (∆ = 0; Pe = 0), то есть когда матрица условных вероятностей переходов представляет собой единичную матрицу.

Таблица 1. Зависимость среднего количества взаимной информации от средней вероятности ошибки и параметра несимметричности

Table 1. Dependence of the average amount of mutual information on the average error probability and the asymmetry parameter

Pe = 0,005		Pe = 0,10		Pe = 0,20
∆	I (∆ ≤ 0,005; Pe = 0,005)	∆	I (∆ ≤ 0,10; Pe = 0,10)	∆	I (∆ ≤ 0,20; Pe = 0,20)
0,0000395	0,9545855	0,0009801	0,5310093	0,0019702	0,2780782
0,0005346	0,9546260	0,0108811	0,5316134	0,0217722	0,2788443
0,001030	0,9547371	0,0207821	0,5332423	0,0415742	0,2809178
0,0015247	0,9549211	0,0306831	0,5359429	0,0613761	0,2843835
0,0020197	0,9551821	0,0405841	0,5397981	0,0811781	0,2893932
0,0025148	0,9555270	0,0504851	0,5449405	0,1009801	0,2961910
0,0030098	0,9559659	0,0603860	0,5515769	0,1207821	0,3051641
0,0035049	0,9565156	0,0702870	0,5600424	0,1405841	0,3169480
0,0040000	0,9572056	0,0801880	0,5709304	0,1603860	0,3326875
0,0044950	0,9580990	0,0900890	0,5855237	0,1801880	0,3548977
0,0049900	0,9594745	0,0999900	0,6099121	0,1999900	0,3957405
Pe =	0,30	Pe =	0,40	Pe =	0,495
∆	I (∆ ≤ 0,30; Pe = 0,30)	∆	I (∆ ≤ 0,40; Pe = 0,40)	∆	I (∆ ≤ 0,495; Pe = 0,495)
0,0029603	0,1187139	0,0039504	0,0290513	0,0048910	0,0000721
0,0326633	0,1192988	0,0435544	0,0292793	0,0539011	0,0000730
0,0623662	0,1208914	0,0831583	0,0299060	0,1029111	0,0000753
0,0920692	0,1235858	0,1227623	0,0309856	0,1519211	0,0000795
0,1217722	0,1275535	0,1623662	0,0326209	0,2009311	0,0000860
0,1514751	0,1330779	0,2019702	0,0349909	0,2499405	0,0000962
0,1811781	0,1406245	0,2415742	0,0384121	0,2989504	0,0001123
0,2108811	0,1509902	0,2811781	0,0434802	0,3479603	0,0001399
0,2405841	0,1656815	0,3207821	0,0514629	0,3969702	0,0001952
0,2702870	0,1881864	0,3603860	0,0657684	0,4459801	0,0003534
0,2999900	0,2363796	0,3999900	0,1079630	0,4949900	0,0049711

Таблица 2. Сравнение симметричного канала и несимметричного канала с максимальной эффективностью

Table 2. Comparison of balanced channel and unbalanced channel with maximum efficiency

Pe	0	0,005	0,1	0,2	0,3	0,4	0,45	0,5
I (∆ → Pe )	1	0,959	0,609	0,395	0,236	0,107	0,051	0
I (∆ = 0)	1	0,954	0,531	0,278	0,118	0,029	0,007	0

Рассмотрим функцию I ( Pe ) при значении параметра несимметричности ∆ → Pe . Соответствующие значения этой функции в некоторых точках приведены в табл. 2.

Для сравнения эффективности симметричного и несимметричного каналов в эту же таблицу добавим значения функции I ( Pe ) при ∆ = Pe .

Анализ табл. 2 позволяет наглядно подтвердить вывод, что при фиксированном значении средней вероятности ошибки среднее количество взаимной информации для несимметричного канала больше, чем для симметричного, то есть информационная эффективность несимметричного канала выше, чем симметричного, при любом значении параметра несимметричности ∆.

Количество информации, выдаваемой недвоичным несимметричным каналом распознавания потребителю

На основе обобщения двоичного несимметричного канала распознавания рассмотрим количество информации, выдаваемой недвоичным несимметричным каналом распознавания потребителю.

Канал распознавания формирует решение (оценку) f[ о принадлежности η наблюдаемого объекта к классам y_i в алфавите объёмом J , j = M . Это решение выдаётся потребителю, формирующему решение о принадлежности ξ наблюдаемого объекта одному из классов x_i заданного алфавита объёмом I , 1 = \Д .

В данном случае показателем качества выдаваемой потребителю информации является среднее количество взаимной (парной) информации о принадлежности ξ наблюдаемого объекта одному из классов x_i алфавита потребителя объёмом I , содержащейся в решении f) канала распознавания

1^п^н^Ун^\^,H где H Q^ и н(а\^– безусловная и условная энтропии.

^HW =^_E v^=yj ) ■ ^lo§2 ^ркп⁼У] )},

7=1

I где P^ = У^ = ^\Р^ = Xi>P^f) = yj \ ^ = ХД, Р^ = У)\^ = х^– вероятность перехода, опре деляемая соотношением

P^ = У) \^ = ^ = ^Р<П = Ук \^ = x_iyP^ = y_j 17 = л)

Вероятности Р yf] = у ^ \ i] = у_к j являются элементами матрицы условных вероятностей распознавания, являющейся обобщением (1), – вероятностей правильных (при j = k ) и ошибочных (при j ≠ k ) частных решений в канале распознавания.

Вероятности Р^т] = у_к | У = xj являются вероятностями перехода от заданного алфавита окончательных (общих) решений к алфавиту частных решений системы распознавания. В [3], как и в [4], эти вероятности характеризуют соотношение между объектами различных классов среди «своих» и «чужих» объектов, отмечается, что не представляет большой сложности на основе описаний классов рассчитать их для конкретной тактической ситуации. В [10] рассматриваемые вероятности являются элементами матрицы, названной MAPPING-матрицей.

MAPPING-матрица имеет следующий вид:

Р(л = Ух К = ЛГ1) Р(т₇ = у₂|^ = х₁) ... Р^ = у_л\^ = х^

К^ = Лк = ^)|| =

Р^ = Ух\У = ч) Р^ = У2\^ = Ч) - Р^ = Ул к = *2) •

Р^ = Ух\У = хт) Р^ = у1\^ = х1) ... р^ = ул\^ = х^

Условная энтропия определяется соотношением

Н ^ I ^ = -^^^р^ = У]^ = ^ )bg₂ Р^ = У]\У = ^х_г )},

7=1 7=1

где Р{fj = уу, с, = x,J = Р(у = x_i у Р^й = у/ I ь ^{= x}i ), P ( £ = xi) — априорная вероятность принадлежности наблюдаемого объекта к классу x_t в заданном алфавите окончательных решений потребителя, вероятности описаны выше.

Рассмотрим случай одинаковых строк в MAPPING-матрице, когда п не несёт никакой информации о ξ – количество взаимной информации должно быть равно нулю. Расчёты подтверждают это.

Так как ноль количества взаимной информации достигается при равенстве строк MAPPING-матрицы, то в качестве параметра зависимости среднего количества взаимной информации, получаемой в результате пересчёта решений канала распознавания к алфавиту окончательных решений потребителя, от структуры (вида) MAPPING-матрицы оправдано использовать среднюю разницу d между её строками:

^{d =} 7 /Ln !LiL\^P^⁼ У к ¹ У ^{= Х}'+1 Ь^Р^⁼ У к I У = ^Х1 )| •

График зависимости среднего количества взаимной информации от вероятности правильного распознавания при различных значениях параметра d представлен на графике (рис. 1).

На графике видно, что среднее количество взаимной информации растет при увеличении средней разницы между строками в MAPPING-матрице при одном и том же фиксированном значении средней вероятности правильного распознавания. Максимум I для заданной матрицы распознавания канала стремится к значению среднего количества взаимной информации при отсутствии MAPPING-преобразования (совпадении алфавитов решений канала и потребителя).

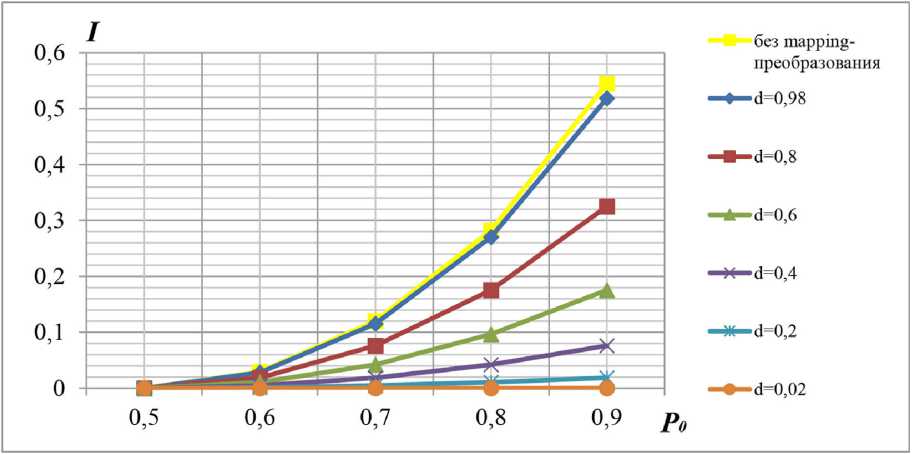
Рис. 1. График зависимости среднего количества взаимной информации от вероятности правильного распознавания при различных значениях параметра d

Fig. 1. Graph of the dependence of the average amount of mutual information on the probability of correct recognition for various values of the parameter d

Количество взаимной (парной) информации в комплексной системе распознавания

Рассмотрим комплексную систему распознавания, объединяющую N разнородных несимметричных каналов распознавания.

Объединяемые каналы распознавания формируют частные решения (оценки) ^п , 77 = 1, N , о принадлежности ηn одного и того же наблюдаемого объекта к классам V„j в своих алфавитах объёмом J_n , in . После объединения частных решений Лп необходимо сформировать окончательное (общее) решение о принадлежности ξ наблюдаемого объекта одному из классов x_i заданного алфавита объёмом I , 1 = \д .

Для такой комплексной системы распознавания информационным показателем её качества является среднее количество взаимной (парной) информации о принадлежности ξ наблюдаемого объекта одному из классов x_i заданного алфавита объёмом I , содержащейся в совокупности частных решений Ли , 77 = 1, N . В данном случае среднее количество взаимной (парной) информации определяется следующим образом

1иЛЛъ---Л1^ = н1п\ЛЬ>---Л1^             , где н<пхаъ_,...,пкУнкп\РЬ-—Пк\^ – безусловная и условная энтропии совокупности частных решений.

Безусловная энтропия равна

^ (771Л2>-"Ллг) = ^{-1оёр(М2>-ЛдО}.

Совместную вероятность частных решений каналов распознавания можно представить в виде

Р ( 7/1,7/2, - ^N ) = 2 Р ( ^ = \ ) Р ( 7/1, //э ,..., f]_N | £ = X, )^.

При заданном £ = xi частные решения каналов распознавания можно считать статистически независимыми (условно независимыми), поэтому

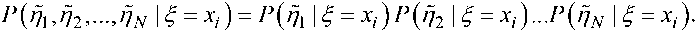
В результате формула для расчёта безусловной энтропии приобретает вид

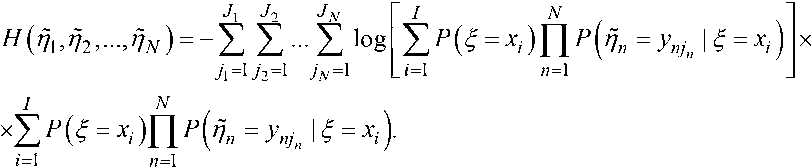
Условные вероятности частных решений рассчитываются по формуле:

Р^п = У^п I £ = ^z) = Е Р(^ = Ункп I § = -^(^ = У^п I Пи = Упк„ )• ^=1

Вероятности                   являются элементами матрицы условных вероятностей распознавания: вероятностей правильных (при jn = kn) и ошибочных (при jn ± kn) частных решений в объединяемых каналах распознавания.

Условная энтропия равна

Н(Д,й2,...,йм | £) = М^-\о§Р(Д,й2,...,йм | £)} = -^Р^ = х^х

Z=1

<У| ^7 N Г"                                                                                                       -1

ХЕ Е"" Е 1°ё^Р(^1=3;и1|^ = ^)Р('72=^2У2|^ = ^)-Р(^=^|^ = ^Ух

71=172=1   7х=1

xP^i = y_Xjx | ^ = x, )p(/7₂ = у_2н | £ = x_t yP^q_N = y_NjN У = x_t)

Рассмотрим применение методики для исследования информационных свойств комплекс -ной системы распознавания на конкретных примерах.

Пример 1. В комплексной системе объединяются три несимметричных канала, задаваемых следующими матрицами условных вероятностей переходов, характеризующими достоверность распознавания:

0,87	0,01	0,06	0,04	0,02
0,02	0,91	0,01	0,03	0,03
0,06	0,03	0,75	о,п	0,05
0,01	0,05	0,04	0,89	0,01
0,08	0,07	0,01	0,01	0,83

0,58	0,19	0,10	0,13
0,10	0,65	о,н	0,14
0,12	0,31	0,54	0,03
0,09	0,13	0,15	0,63

0,98 0,02

0,12 0,88

В соответствии с этими матрицами средние вероятности правильного распознавания имеют следующие значения: P ₀₁ = 0,85, P ₀₂ = 0,60, P 03 = 0,93.

После объединения должно быть сформировано окончательное (общее) решение о принадлежности наблюдаемого объекта в алфавите объёмом I = 4. Причём алфавит второго канала совпадает с алфавитом окончательных решений.

Связь между алфавитом окончательных решений и алфавитами частных решений каналов задаётся MAPPING-матрицами:

	0,31 0,15 0,18 0,25 0,11		10 0 0		0,95 0,05
	0,29 0,17 0,21 0,23 0,10		0 10 0		0,3   0,7	.
	0,33 0,15 0,20 0,22 0,10		0 0 10	9	0,84 0,16
	0,34 0,19 0,23 0,19 0,05		0 0 0 1		0,09 0,91
MAPPING-матрицы 1 и 3 каналов характеризуются следующими средними разницами
между строками: d 1	= 0,02267, d 3 = 0,6467.

Значения информационного показателя качества различных вариантов комплексной системы распознавания, объединяющей заданные несимметричные каналы распознавания, представлены в табл. 3. Для сравнения представлено среднее количество взаимной информации, Ч^^) , содержащейся в частных решениях каналов о принадлежности объектов к классам в заданном алфавите окончательных (общих) решений.

Пример 2. По сравнению с примером 1 изменены матрицы условных вероятностей распознавания 1 и 3 каналов:

0,93	0,01	0,02	0,03	0,01
0,02	0,87	0,03	0,02	0,06
0,01	0,01	0,96	0,01	0,01
0,01	0,05	0,02	0,91	0,01
0,04	0,07	0,03	0,03	0,83

0,58 0,19

0,10 0,65

0,12 0,31

0,09 0,13

0,10 0,13

0,11 0,14

0,54 0,03

0,15 0,63

0,75 0,25

0,35 0,65

P 01 = 0,9, P 02 = 0,6, P 03 = 0,7.

Результаты вычислений занесены в табл. 4.

Из сравнения табл. 3 и 4 следует – несмотря на то, что в примере 2 (табл. 4) распознавание в третьем канале менее достоверно, чем в первом, третий канал более информативен, чем

Таблица 3. Значения информационного показателя качества комплексной системы распознавания (пример 1)

Table 3. The values of the information indicator of the quality of the complex recognition system (example 1)

№ канала	i^n^		ЧМ1ЛЛ	1^2,^	1^-ЛъП2Лз)
1	0,005	0,496	0,283	0,697	0,700
2	0,491
3	0,278

Таблица 4. Значения информационного показателя качества комплексной системы распознавания (пример 2)

Table 4. The values of the information indicator of the quality of the complex recognition system (example 2)

№ канала 4^4 Ч^х^Ч 1^2^ 1^;п\,п2,пз) 1 0,006 0,496 0,068 0,536 0,541 2 0,491 3 0,062 первый, как и в примере 1 (табл. 3), где соотношение между достоверностями распознавания в этих каналах обратное. Это объясняется структурами MAPPING-матриц, используемых для пересчёта алфавита частных решений каналов к алфавиту окончательных (общих) решений комплексной системы: строки в MAPPING-матрице третьего канала больше отличаются друг от друга (d3 = 0,6467), чем строки в MAPPING-матрице первого канала (d3 = 0,02267). Второй канал более информативен по сравнению с двумя другими каналами, несмотря на самую низкую достоверность распознавания в нём. Это объясняется тем, что алфавит частных решений второго канала совпадает с алфавитом окончательных (общих) решений комплексной системы: MAPPING-матрица единичная.

Таким образом, структура MAPPING-матриц, используемых для пересчёта алфавитов каналов к алфавиту комплексной системы, оказывает большее влияние на количество информации, получаемой на выходе комплексной системы, чем средняя вероятность правильного распознавания в каналах.

Данный вывод, сделанный на основе применения обобщённой методики исследования информационных свойств, согласуется с выводом, сделанным в [3] на основе статистического анализа задачи комплексного опознавания: изменение соотношения своих и чужих объектов среди представителей одного класса всегда оказывало большее влияние на достоверность опознавания, чем собственно вероятность правильного распознавания классов объектов.

Применение обобщённой методики исследования информационных свойств также позволяет сделать вывод об эффективности использования косвенной информации (каналы 1, 3) о принадлежности объекта к классам в алфавите окончательных (общих) решений. В представленных выше примерах объединение основного канала 2 (канала, алфавит которого совпадает с алфавитом системы) с каналами 1, 3 с косвенной информацией (каналами, алфавиты которых не совпадают с алфавитом системы) увеличило количество получаемой информации на 10–40 %.

Заключение

Таким образом, в работе на основе последовательного анализа количества информации на выходе двоичного несимметричного канала распознавания, затем количества информации, выдаваемой недвоичным несимметричным каналом распознавания потребителю с отличающимся алфавитом классов, предложена обобщённая методика исследования информационных свойств каналов и систем распознавания, применимая для анализа комплексных систем распознавания.

Применение методики показало, что при объединении разнородных каналов для распознавания эффективно использование не только прямой, но и косвенной информации.