Обоснование физических основ буровзрывного способа для получения строительных материалов из природного камня

Разработка месторождений блочного камня должна вестись с позиций ресурсосбережения и рационального использования этого ценного минерального сырья с сохранением его естественных физико-механических свойств. При разработке в основном используется буровзрывной способ отбойки блоков, при котором выполнение указанных требований является весьма сложным. Применяемые технологии взрывной отбойки камнеблоков обеспечивают в настоящее время выход качественного блочного камня лишь в пределах 20–25% от объема добываемой горной массы [1]. Поэтому решение этой актуальной проблемы повышения выхода качественной продукции должно базироваться на совершенствовании способов управления энергией взрыва и разработке физических основ направленного разрушения горных пород для обоснования технологий щадящего взрывания, при которых обеспечивается сохранность прочностных свойств добываемых блоков и законтурного массива.

В связи этим необходима разработка новых физических методов направленного разрушения горных пород. Для решения данной проблемы целесообразен системный подход, учитывающий весь спектр вопросов эффективного управления энергией взрыва, что является актуальной научной проблемой и позволит выявить существенные резервы для увеличения объемов добычи и уменьшения себестоимости качественных строительных материалов из природного камня. Известно, что с увеличением

ВЕСТНИК БУРЯТСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА

3/2012

расхода взрывчатых веществ на один погонный метр длины заряда растет расстояние между смежными скважинами (шпурами) и, соответственно, увеличивается зона нарушенности законтурного массива. Таким образом, масса заряда и расстояние между ними находятся в противоречии с обеспечением сохранности тыльной стороны массива: чем больше это расстояние, тем большими будут размеры зоны нарушенности законтурного массива. Поэтому необходимо обоснование рационального соотношения между величиной заряда и расстоянием между шпурами (скважинами) в ряду, для чего нужно использовать взаимосвязь амплитудно-временных параметров импульса давления продуктов взрыва (ПВ) в зарядной камере с интенсивностью формирования волн напряжений.

При возникновении магистральной трещины по линии расположения шпуров (скважин) происходит остановка развития побочных (азимутальных) трещин за счет разгрузки контурной части, что экспериментально доказано многими исследователями. Процесс развития магистральной трещины при хрупком разрушении наиболее адекватно описывается критерием А.Ф. Иоффе – критерием максимальных растягивающих напряжений. Условием продвижения трещины является соблюдение локального уровня напряженно-деформированного состояния в области острия трещины, когда деформация у вершины движущейся трещины инвариантна и равна критической.

Учитывая, что область массива между смежными зарядами подвержена квазистатическому напряженному состоянию за счет установления равномерного нагружения горной породы давлением продуктов взрыва, то целесообразно определить длину магистральной трещины путем приведения динамической задачи к статической. Для определения максимальной длины развития магистральных трещин воспользуемся моделью Дагдайла-Билби-Коттрелла-Свиндена, в которой применена теория непрерывно распределенных дислокаций [2]. При этом теорией линейной механики разрушения до- пускается, что разрушение наступает тогда, когда раскрытие трещины в вершине достигает некото- рого критического значения 5о. Раскрытие трещины вычисляется по формуле:

δ

4 L ■ а „ ■ sin а кр

п ² ■ E

π

₂             cos K

■ J 1 - sin ² а ■ sin ² K

■ 1n

sin sin

( к ( к

+ Ф ) — Ф )

dK ,

где

sin ф = cos

πσ

2 σ кр

тр sin а = sin -------

L где L–расстояние между шпурами (скважинами), см; σкр–-критическое растягивающее напряжение, МПа; Е -модуль Юнга, МПа; σ – растягивающее напряжение, МПа; lтр – длина радиальной трещины, см; х – расстояние от центра зарядной полости до оси симметрии между зарядными, см.

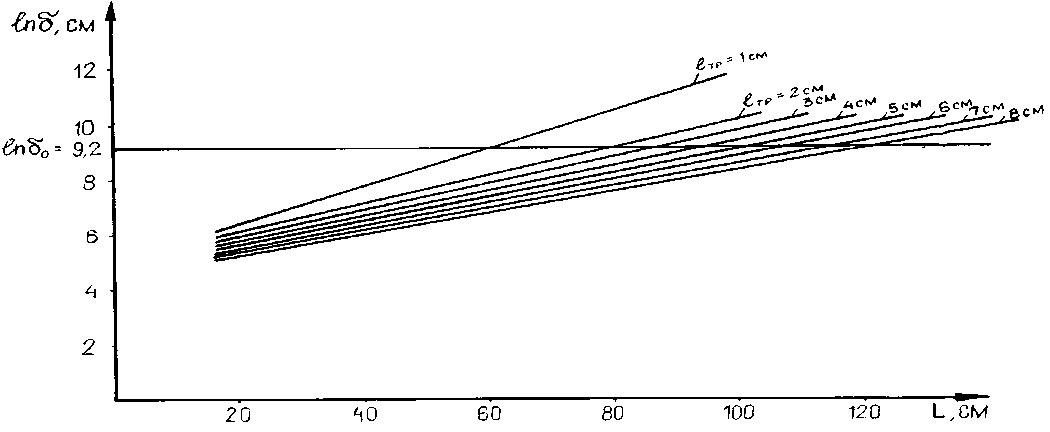
Рис. Зависимость раскрытия трещин ( 5 ) от расстояния между зарядными полостями

Результаты расчетов раскрытия трещин представлены в виде графиков на рис. При этом используется критерий разрушения, который основан на допущении определенного раскрытия трещин, т.е. разрушения при достижении некоторого критического значения, в нашем случае равного 5 0 = 340^- 4 см. Из графика видно, что каждой длине радиальной трещины (1_тр) существует

Б.Г. Базаров, У. Чинсух, С. Норжинбадам и др. Суперпластификаторы на основе отходов угледобывающей и деревообрабатывающей промышленности при производстве строительных материалов максимальное расстояние между шпурами (скважинами). Приведенные расчетные зависимости для определения максимальных расстояний между зарядными полостями L и не превышают размеры зон нарушенности блочного камня, согласно требованиям ГОСТ 79-84.

Таким образом, процесс раскола блочного камня отражает физическую модель направленного разрушения горных пород и может служить основой для выбора оптимального расстояния между шпурами (скважинами).