Обоснование формулы для количественной оценки дефицита сейсмостойкости зданий нелинейным статическим методом в SAP2000

1. Актуальность оценки дефицита сейсмостойкости зданий

В сейсмических районах всегда будут происходить землетрясения. Ликвидация последствий повреждений зданий всегда связана с огромными затратами сил и материальных средств. Известно, что сейсмоусиление зданий априори является дорогостоящим мероприятием и зависит от интенсивности сейсмического воздействия, прогнозируемого на площадке. Согласно информации, представленной на заседании Комитета Совета Федерации по федеративному устройству, региональной политике, местному самоуправлению и делам Севера (протокол от 22.11.2019 г. № 209), всего за период 2002–2018 годов на реализацию мероприятий по сейсмоусилению объектов было направлено порядка 41 235,8 млн рублей. Если объем требуемых антисейсмических мероприятий на стадии перед их внедрением в здание будет технически недооценен, то это может выразиться в формировании в нем дефицита сейсмостойкости (далее ‒ I_d ).

Разные специалисты трактуют термин «дефицит сейсмостойкости» по-разному, выполняя оценки Id с учетом специфики решаемых ими задач. В работах, содержащих численные и (или) аналитические результаты оценки дефицита сейсмостойкости, такая оценка, как правило, сводится к сопоставлению интенсивностей сейсмических сил, рассчитанных для стадии проектирования и после уточнения расчетной информации. Дефицит сейсмостойкости сооружения, например, одни исследователи определяют разностью между сейсмостойкостью зданий и сейсмичностью грунтов, другие – как разность между расчетной балльностью здания по существующим нормам проектирования и фактическим уровнем его сейсмостойкости; еще интерпретируют как расхождение между требуемым и фактическим (оценочным) уровнями сейсмостойкости или как разность между требуемой расчетной сейсмостойкостью здания и фактической, определяемой годом постройки, категорией грунтов по сейсмическим свойствам и др. При этом принимается, что дефицит сейсмостойкости определяют в предположении, что сейсмостойкость здания априори соответствует расчетной балльности площадки. Применяется предпосылка, что здание, спроектированное по нормам, обязательно выдер- жит землетрясение, которое учитывалось при проведении расчетов. Перечисленные выше особенности определения термина «дефицит сейсмостойкости» следует признать общими, позволяющими провести только укрупненные оценки величины Id, поскольку сейсмостойкость здания, подтвержденная только теоретически, как правило, отличается от его фактической способности сопротивляться землетрясению.

Естественным будет предположить, что величина I_d будет зависеть не только от интенсивности землетрясения, но и от срока эксплуатации здания к моменту проведения оценки дефицита сейсмостойкости. Факт того, что со временем несущие конструкции зданий и сооружений изнашиваются, отрицать нельзя. Но если к концу срока эксплуатации здание не подвергалось воздействию расчетного землетрясения, то здание не превращается в одночасье в груду строительного мусора. Примером тому могут служить объекты культурного наследия, которые находятся в сейсмических районах (например, во Владикавказе, в Иркутске, Улан-Удэ). Даже спустя столетие многие из таких зданий сохранились, поскольку в районе их расположения не было сильных землетрясений.

Величину дефицита сейсмостойкости принято оценивать в баллах макросейсмической шкалы путем математического округления до целого значения. Расчетный балл сейсмической интенсивности связывают с конкретной величиной ускорения колебаний в уровне основания. Измерение дефицита сейсмостойкости в баллах следует рассматривать как вынужденную меру, поскольку к понятию «балл» привязаны обязательные конструктивные мероприятия, регламентируемые правилами проектирования, и имеющиеся статистические оценки затрат на сейсмоусиление строительных конструкций [1, 2]. Но в правилах проектирования не приводится формула для количественной оценки дефицита сейсмостойкости. При этом если приращение сейсмической интенсивности для площадки при проведении сейсмического микрорайонирования может быть определено с точностью до 0,01 балла, то почему бы тогда для оптимизации мероприятий по сейсмоусилению с точностью хотя бы 0,25 балла не вычислить величину Id для здания, расположенного на той же площадке, или иным практически удобным способом (числом или мерою) оценить дефицит сейсмостойкости здания.

Настоящая статья является продолжением исследования, результаты которого опубликованы в работах [3, 4]. Для определения величины I d железобетонного каркаса здания, рассчитанного нелинейным статическим методом в SAP2000, в указанных работах приведено выражение вида (в операторах MathCAD):

Id = round.

log

SF (1

—

0.5

¹ ex \

Tj

, I

2  ,  (1)

где i – индекс в основании логарифма, зависящий от увеличения сейсмического эффекта с повышением интенсивности землетрясения на один балл макросейсмической шкалы (учитывает так называемый переход между баллами); T_ex – фактический срок эксплуатации здания (в годах); T_st – срок службы здания (в годах); SF – поправочный коэффициент к входному спектру воздействия, построенному с затуханием 5 % в осцилляторах (приме-

няется для визуализации результатов расчета любой из нелинейных расчетных процедур в SAP2000).

• 2.    Поправка за возраст здания

Знаменатель дроби в формуле (1) представлен двумя множителями; второй имеет вид:

(1 -^Г .             (2)

T st

Далее выражение (2) будем называть поправкой за возраст здания, которая была введена в выражение (1) для целей учета влияния выработанного ресурса здания на величину Id. Поскольку физический износ является закономерным явлением, то эта поправка была принята, чтобы учесть старение и постепенное ухудшение качества строительных элементов в процессе эксплуатации здания (за счет накопления повреждений, обусловленных слабыми частыми землетрясениями, влиянием коррозии арматуры и др.) до первого капитального ремонта с сейсмоусилением. Указанная    поправка    является    множителем к коэффициенту SF.

Что определяет собой SF: это коэффициент, соответствующий положению точки, характеризующей напряженно-деформируемое состояние и упруго-пластические свойства изучаемой системы, на ее кривой равновесных состояний при допускаемом уровне повреждений конструкций (далее – контрольная точка). Назначается SF относительно положения редуцированного спектра, проходящего через контрольную точку, с учетом способности изучаемой системы к рассеянию энергии колебаний за счет гистерезисного поведения. Переход от одного представления редуцированного спектра к другому через применение SF осуществляется в зависимости от уровня допускаемых поврежде-

ний. При этом указанный коэффициент может учитывать переход между спектрами как на уровне постоянных ускорений, так и на уровне постоянных скоростей смещений. К исходному спектру воздействия в применяемой нелинейной статической процедуре Capacity Spectrum Method (АТС40. Seismic Evaluation and Retrofit of Concrete Buildings; 1996) для участков с постоянными ускорениями и постоянными скоростями коэффициенты редукции SR_A и SR_V определяются по разным формулам, соответствующим результатам исследований Ньюмарка – Холла (1982). Этапом, предваряющим вычисление коэффициентов редукции, является оценка суммарного затухания системы (пояснено в [5]). Как влияет значение коэффициента SF на величину I d , показано в таблице результатов работы [3].

Изначально выражение (1) формировалось на основе простого условия, чтобы при множителе SF, равном 1,0, для нового здания значение I_d было бы равно 0. При назначении величины i учитывалось, что с увеличением интенсивности на один балл средние значения амплитуды ускорения сейсмических колебаний увеличиваются в два раза. Такая закономерность нарастания ускорений описывает связь ускорения с цифрой балльности J . Вот только ограничения формулы (1) в работе [3] были раскрыты не полностью, поскольку дефицит сейсмостойкости определялся для каркаса здания, возведенного для целей проведения натурного вибрационного эксперимента. В процессе рабочего тестирования выражения (1) возник вопрос о том, почему (за счет каких факторов) у здания, которое в течение всего периода эксплуатации не подвергалось воздействию расчетного землетрясения, при неизменной информации о сейсмологических условиях в конце срока службы только за счет поправки за возраст по формуле (1) формируется дефицит сейсмостойкости более двух баллов. Для поиска ответа на указанный вопрос пришлось изучить результаты исследований Я.М. Айзенберга, В.А. Быховского, А.Н. Добромыслова, А.И. Мартемьянова, С.В. Медведева, А.И. Неймана, Н.И. Фроловой и др. Исходя из этого, в статье будет рассматриваться только влияние поправки за возраст здания на объективность оценки величины его дефицита сейсмостойкости.

Выражение (2) было заимствовано автором из «Методики…» [6] (в пояснительной записке к которой приведена ссылка на работу [7]), где указано, что за счет снижения обеспеченности появления 9-балльного землетрясения за оставшийся срок службы здания допускается снижать сейсмическую нагрузку у «старых» зданий. Согласно указанной «Методике…» снижение расчетной амплитуды производится по следующей формуле:

0.5

а ст = А . (^ о-) , (3)

где А ст – расчетная амплитуда воздействия для «старого» здания; А н – расчетная амплитуда воздействия для нового здания; Т ос – оставшийся срок службы здания (в годах); Т н – срок эксплуатации нового здания, принятый равным 100 лет. Множитель к расчетной амплитуде воздействия А н применяется здесь для уменьшения амплитуды ускорения ожидаемого сейсмического воздействия. Предполагается, что такой подход предпринят для целей оптимизации затрат на сейсмоусиление «старых» зданий. В оригинале формула (3) представлена в виде:

1 2 ^0.5

А 2 = А 1 ^rj , (4) где через τ ₁ обозначен срок службы вновь построенного сооружения, а через τ ₂ ‒ остаточный срок службы эксплуатируемого сооружения; обозначение A ₂ эквивалентно обозначению А _ст, а А ₁ – значению А н в выражении (3). Отмечается, что указанное выражение справедливо при фиксированной (постоянной) вероятности того, что за срок службы сооружения τ не произойдет ни одного землетрясения с интенсивностью, превышающей заданную величину J. Принималось, что при одной и той же вероятности изменение расчетного срока службы τ вызывает изменение расчетного ускорения пропорционально квадратному корню из отношения указанных сроков службы. Выражениями (3) и (4) учтены особенности, основанные на региональных наблюдениях. Ценность выражения (4) состоит в том, что, несмотря на упрощения и предпосылки, заложенные в его основу, им определяется подход к практической реализации требований правил проектирования к учету износа зданий в конце срока службы.

Правый множитель в выражениях (3) и (4) по своей сути схож с выражением (2), но последнее в настоящей работе наделено одним важным концептуальным отличием. В выражении (1) поправка за возраст, в отличие от учтенной в выражениях (3) и (4), применяется не на стадии оценки интенсивности расчетной сейсмической нагрузки, а на стадии формирования траектории поиска той контрольной точки, которая на кривой равновесных состояний изучаемой системы определяет неупругое поведение последней при действии нагрузок типа сейсмических.

В настоящей работе не будут рассматриваться особенности вывода формулы (4) средствами математики. Попытаемся понять, насколько математическое представление выражения (4) отражает физическую сущность такого явления, как повторяемость землетрясений в одной и той же местности.

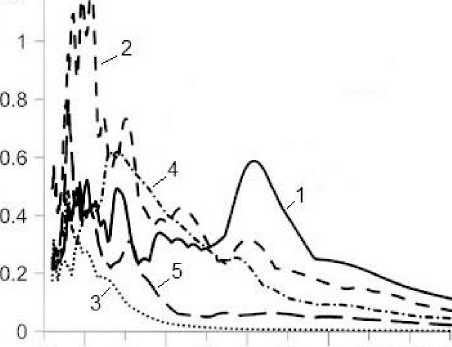
Рассмотрим землетрясения (рис. 1), произошедшие в районе Кентербери (Новая Зеландия) с разницей всего в полгода.

Сначала 04.09.2010 г. произошло Дарфельд-ское землетрясение с магнитудой М = 7,1 (характеризующееся вероятностью возможного превышения 0,0952 в течение 50 лет), а уже 22.02.2011 г. случилось сильное землетрясение с М = 6,3 (характеризующееся вероятностью превышения 0,0198 в течение 50 лет), потрясшее г. Крастчерч. Хотя последнее по магнитуде было меньше, обладало иным частотным составом и преобладающим периодом (к слову, эти особенности учитываются коэффициентом SF), но эпицентр последнего из указанных землетрясений был сосредоточен ближе к городу, что вызвало значительно бόльшие повреждения. Получается, что пояснения, заложенные в основу выражения (4), могут не согласовываться с картиной проявления землетрясений на одной и той же местности. Рассмотренный пример показывает, что уменьшение остаточного срока службы не может снижать вероятности реализации

Sa(g)

0       1       2       3       4 T(sec)

Рис. 1. Графическая визуализация спектров реакции землетрясений, произошедших в районе Кентербери в период с 2010 г. по 2011 г. [8]: 1 – спектр реакции землетрясения, произошедшего 04.09.2010 г.; 2 – спектр реакции землетрясения 22.02.2011 г.; 3 – 26.12.2010 г.;

4 – 13.06.2011 г.; 5 – 23.12.2011 г.

сильного землетрясения за оставшийся срок эксплуатации здания.

Поскольку повторяемость землетрясений обычно связывают со сроком эксплуатации здания, выражаемым какой-то конечной величиной, поэтому важно учесть понятие о возрастных и невозрастных объектах [9]. Объект считается безвоз-растным, если вероятность существования объекта в течение определенного интервала времени не зависит от времени, которое объект уже существовал. Таким свойством, например, не обладает человек, так как чем он старше, тем с большей вероятностью его не станет в течение заданного промежутка времени. При этом существует временной интервал, в рамках которого течение возраста объекта не так заметно, как в конце рассмотренного интервала времени. Эти положения с незначительными поправками справедливы и для здания, и их нужно учитывать.

Суммарные затраты на ремонтно-восстановительные работы и нормативный срок окупаемости антисейсмических мероприятий зависят от периода повторяемости землетрясений в течение срока службы здания [10]. Принимается, что при эксплуатации в результате физического износа здания его стоимость убывает по экспоненциальному закону, имеющему теоретическое обоснование и согласующемуся с экспериментальными результатами [10–12], что определяется выражением вида:

Q(t) = 1 + e-"6,                (5)

где Q ( t ) ‒ величина износа здания (сооружения) к моменту реализации расчетного землетрясения; t ‒ время эксплуатации здания от начала эксплуатации до учитываемого землетрясения (в годах); λ ‒ коэффициент, характеризующий относительную ежегодную скорость износа здания. Отсюда величина e^‒λt ‒ это так называемая мера сохранности здания к моменту времени t. Физический износ здания согласуется с уменьшением стоимости здания с возрастом. В работе [10] отмечается, что стоимость здания в год t с учетом его износа определяется из выражения

C t = C o x e ^-"⁶ ,                  (6)

где через С0 ‒ начальная стоимость здания (сооружения). Эту информацию примем за основу для формулировки следующего условия. Примем, что: (а) если бы сколько-нибудь ощутимое землетрясение, способное нанести зданию видимые повреждения, не произошло за время его эксплуатации; (б) если бы произошедшее событие не превышало прогнозируемое расчетное землетрясение; (в) если бы здание показало бы себя надежным при таком расчетном событии, ‒ то это было бы достоверно известно. На основании такого условия величину e‒λt в выражениях (5) и (6) можно отождествить с величиной   e‒pt,   полученной с учетом распределения Пуассона. Тогда при указанном условии примем, что прошедший срок здания, эксплуатируемого в сейсмическом районе, с учетом его реального износа будет описываться распределением e‒pt.

Итак, любое здание является возрастным объектом; срок службы здания состоит из суммы существующего периода эксплуатации и остаточного срока службы. Физический износ здания, реализовавшийся к дате проведения оценки, влияет только на величину значения прошедшего срока эксплуатации. Распределение e‒pt будет характеризовать степень сохранности здания за прошедший период эксплуатации без расчетного землетрясения. Основываясь на сформулированных положениях, определим прошедший срок эксплуатации здания (в годах) из выражения вида

T = TeX e Pt", (7)

где T ex ‒ то же, что в формуле (1); p ‒ сейсмическая сотрясаемость территории, на которой расположено здание, от s -балльных землетрясений, в годах ^‒1; t_w ‒ время ожидания, в годах; pt_w ‒ математическое ожидание указанного распределения.

• 3.    Приведенный срок службы здания

Для того чтобы учитывать уменьшение стои- мости здания с возрастом, нужно рассмотреть понятие о приведенном сроке службы здания. Установлено [12], что затраты на сейсмоусиление и убытки от землетрясения, как правило, не сопоставимы (то есть с экономической точки зрения, они не эквивалентны). Так, повышение балльности на один балл ведет к увеличению затрат на обеспечение сейсмостойкости здания в размере 3–6 % общей стоимости его строительства. При этом занижение балльности на один балл, которое потом может привести к ущербу при землетрясении, сопровождается затратами на восстановительные работы в размере уже 10–20 % общей стоимости строительства. Для суммирования разновременных затрат (первоначальных и последующих за срок эксплуатации) их необходимо привести к одному периоду времени [11, 12]. Для учета указанных различий за базу приведения, как правило, принимается первый год эксплуата- ции здания после осуществления первоначальных затрат. Затраты последующих лет делятся на коэффициент, определяемый из выражения:

^{K t}    (1+ Е )

где Ен.п ‒ норматив приведения разновременных затрат к одному периоду времени; установлен равным 0,08 по Типовой методике определения экономической эффективности капитальных вложений [12]; tпр ‒ период приведения (в годах), определяемый временем между моментом осуществления первоначальных затрат и моментом производства восстановительных работ на объекте (в нашем случае моментом оценки дефицита сейсмостойкости). При этом приведение затрат на ремонтновосстановительные работы от будущих землетрясений как единовременных (дискретных) не представляется возможным, так как на момент прове- дения такой оценки будет неизвестен период приведения tпр.

С применением коэффициента K t после ряда вычислений определяется коэффициент φ, учитывающий приведение отдаленных во времени затрат к единовременным, то есть к моменту проведения восстановительных работ:

P = T Kt,

где T ₀ ‒ остаточный срок службы здания, в годах (обозначение принято по [11]). Графическое представление зависимости коэффициента ф от продолжительности эксплуатации здания и норматива приведения в [11] определяется по зависимости вида

P(T o ) =

(1+ Енп) To - 1

(1 + Енп) To Енп ’

Отметим, что в работе [12] выражение (10) было представлено в несколько ином виде:

P(T o ) =

(1 + Ен.п) Х Т0 - 1

(1 + Енп) X To X Ен.п■

Указанные зависимости в графическом виде представлены на рис. 2.

Из графического представления зависимости коэффициента приведения ф(Т 0 ) следует, что при достижении зданием срока службы, определяемого значением 50 лет, на обеих кривых начинает формироваться плато с отклонением графика от горизонтали, не превышающим 1 %, и значение коэффициента ф становится практически постоянным. Отсюда можно принять, что после достижения зданием возраста 50 лет затраты, произведенные на его сейсмоусиление, и убытки от повреждения такого здания при ожидаемом расчетном землетрясении могут быть условно приравнены. То есть после достижения зданием указанного возраста можно предполагать некую условную бесконечность его срока службы.

• 4.    Основные положения к обоснованию формулы для оценки Id

В дальнейшем при уточнении выражения (1), такой срок службы будем называть приведенным сроком эксплуатации здания. Будем принимать, что модель накопления дефицита сейсмостойкости здания со временем должна соответствовать растущей модели. Учтем, что понятие расчетного балла непосредственно предполагает, что в рассматриваемой местности в течение расчетного срока службы здания может произойти одно землетрясение интенсивностью J . Примем, что вне зависимости от частоты повторяемости землетрясений в контрольной площадке за время эксплуатации проверяемого здания ожидаемое расчетное землетрясение произойдет. Следовательно, вероятность возникновения ожидаемого расчетного землетрясения должна так влиять на величину дефицита сейсмостойкости, что при уменьшении периода повторяемости сотрясений дефицит сейсмостойкости имел бы приемлемую величину. Будем считать, что величина дефицита сейсмостойкости не может сильно увеличиваться только за счет поправки за возраст сооружения, но должна только немного дополнять значение величины дефицита сейсмостойкости, определяемого параметрами спектра реакции (то есть определяемого коэффициентом SF). При малом сроке эксплуатации здания (до первого капитального ремонта) дефицит сейсмостойкости практически не должен формироваться поправкой за возраст. Принимая во внимание результаты исследований [11, 12], будем учитывать, что при рассмотрении приведенного срока эксплуатации поправка за возраст здания должна вносить в формирование величины дефицита сейсмостойкости надбавку, соизмеримую с ошибкой оценки силы землетрясения. Будем принимать такую ошибку равной ±¹⁄₄ балла [13].

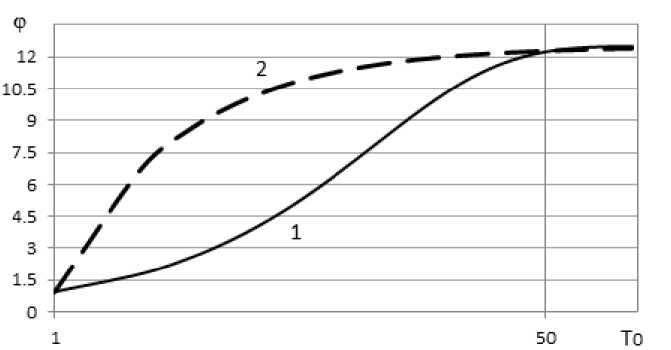
Рис. 2. Графическое представление изменения коэффициента приведения φ [11, 12] в зависимости от продолжительности эксплуатации объекта при нормативе приведения Е н.п = 0,08 и при T 0 , достигающем 100 лет:

1 – кривая, полученная с применением выражения (10);

2 – кривая, полученная с применением выражения (11).

Значения вдоль оси абсцисс отложены по логарифмической шкале

Сейсмостойкость здания при нормальной эксплуатации в сколько-нибудь значимой степени снижаться не будет. Будем отталкиваться от того, что если за время эксплуатации здания величина сейсмического воздействия не превышала расчетную, то, приближаясь к концу срока службы, такое здание под действием слабых землетрясений и других эксплуатационных воздействий, действительно, может прийти в техническое состояние, характеризуемое категорией «ограниченно работоспособное» ‒ но не ниже указанной категории. В соответствии с пояснениями, представленными в Обосновании к [6], указанная категория характеризуется проявлением дефектов и повреждений, соответствующих степени повреждения зданий до d _ср = 3, которые приведут к дефициту сейсмостойкости до 1,5 балла. То есть если принять, что в течение срока службы здания оно не подвергалось воздействию расчетного землетрясения (характеризующегося вероятностью превышения 0,3935 в течение 50 лет), то такое здание не могло в конце срока службы получить повреждения больше третьей степени. На основании результатов исследований [10] будем принимать, что между указанной степенью повреждения здания и показателем физического износа имеется следующее соотношение: физический износ здания будет составлять примерно 40–60 %, коэффициент износа будет определяться равным 0,57. При четвертой степени повреждения коэффициент износа будет равен 1,0 (здесь ‒ коэффициент износа есть отношение стоимости износа здания к восстановительной стоимости здания). Далее учтем результаты работы [14], в которой со ссылкой на доклад, опубликованный в 1974 году Объединенным комитетом по безопасности конструкций при ЮНЕСКО приводится информация о том, что при справедливости закона Пуассона для оценки вероятности сильных землетрясений за определенное время при одной и той же вероятности отсутствия превышения воздействий изменение расчетного срока службы сооружения T р вызывает изменение расчетного ускорения пропорционально кубическому корню из T р . Для графического представления пояснений, указанных в настоящем абзаце, с учетом выражения (7) скорректируем выражение (2), представив его в виде

0.333

—

Построим график зависимости коэффициента износа здания от срока его эксплуатации (рис. 3).

• 5.    Уточненная формула для оценки дефицита сейсмостойкости

В итоге, принимая во внимание все вышерассмотренные пояснения, выражение (1) уточним до вида

I d

= round

— 1 ■

log

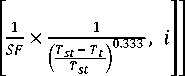
где T t ‒ возраст здания, определяемый из выражения (7); остальные обозначения те же, что в выражении (1). Единичный множитель со знаком «минус» добавлен для удобства идентификации запаса или дефицита сейсмостойкости здания.

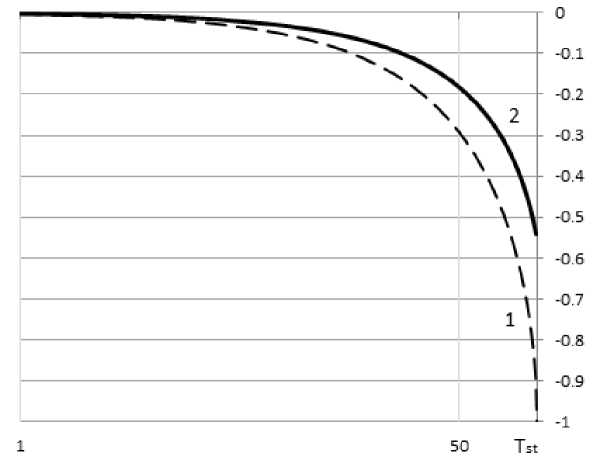
Рис. 3. Графическое представление зависимости коэффициента износа здания от срока его эксплуатации Tst, достигающего 100 лет: 1 – кривая, полученная с применением выражения (2); 2 – кривая, полученная с применением выражения (12). Значения вдоль оси абсцисс отложены по логарифмической шкале

Применим упрощенное выражение для вычисления средней частоты проявления землетрясений, полученное на основе теоремы Байеса, предложенное в работе [15]; в выражение (13) значение T t введем в виде

T_t = T_ex e ^{(1 +} (B s t w ) ^{71 +} 1 ) ,              ⁽¹⁴⁾

где n ‒ число    наблюдаемых    землетрясений в течение времени tw;  остальные обозначения те же, что в выражении (7).

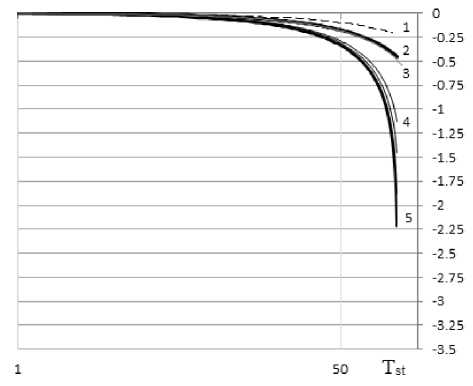
При тестировании формулы (13) были получены графические результаты, представленные на рис. 4.

Из рис. 4 следует, что кривая, полученная с применением выражения (1), почти идеально ложится на кривую, полученную из выражения (13) при учете повторяемости землетрясений один раз в 5000 лет. При повторяемости один раз в 100 лет, при периоде расчетной эксплуатации 100 лет, ближе к концу срока эксплуатации здания поправка за возраст в выражении (13) к величине дефицита сейсмостойкости добавляет не более 0,5 балла, что при прочих равных условиях выглядит намного объективнее, чем дефицит сейсмостойкости, определяемый величиной более 2 баллов, полученный из выражения (1). Величина Id для зданий массового строительства в конце срока эксплуатации по формуле (13) составляет не более 1,25 балла, что согласуется с принятыми положениями Методики [6]. Величина Id, определенная при учете повторяемости землетрясений один раз в 100 лет для здания в конце срока службы, не превышает допускаемую ошибку оценки силы землетрясения. То же, но с учетом выражения (14) при n = 1, величина Id определяется значением 0,5 балла (кривая 3 на рис. 4а). При этом такая кривая 3 получилась количественно и качественно схожей с кривой 2, полученной из выражения (13) при указанных параметрах повторяемости сотрясений.

• 6.    Основные выводы

  В графическом виде приведено обоснование формулы (13), предлагаемой для проведения оценки величины I d с применением нелинейных статических расчетных процедур, реализованных в SAP2000. В формулу оценки I d введена поправка на возраст здания, учитывающая прошедший период его эксплуатации, оставшийся срок службы и значение математического ожидания числа сейсмических событий. Консервативность оценки величины дефицита сейсмостойкости, в зависимости от фактического срока эксплуатации здания и периода повторяемости землетрясений, не превышает 25 % от оценки, выполненной без учета указанной поправки за возраст. Анализ полученных графических результатов показывает, что положения, рассмотренные для целей формирования формулы (13), выполняются. Предложенная формула будет уточняться по мере накопления материалов

а)

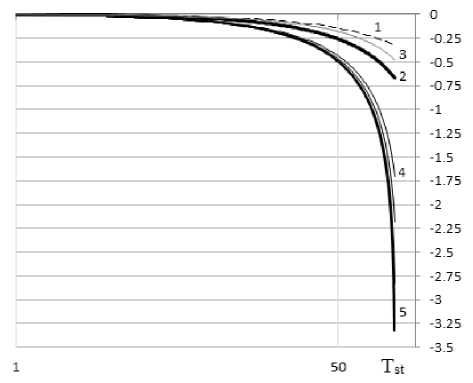
Рис. 4. Графическая интерпретация зависимости величины дефицита сейсмостойкости здания от его возраста при значениях SF = 1, i = 2, T st = 100, t пр = 50 при различном значении математического ожидания ежегодного числа сейсмических событий:

на рис. 4а кривые получены с применением положений и уточнений, рассмотренных в настоящей статье; на рис. 4б – получены при подстановке показателя степени 0,5 вместо 0,333

б)

На рис. 4 представлены следующие кривые: 1 – кривая, полученная с применением формулы (13) при повторяемости землетрясений один раз в 50 лет; 2 – то же, что и кривая 1, при повторяемости один раз в 100 лет; 3 – то же, что и кривая 2, полученная по формуле (13) с учетом выражения (14); 4 – то же, что и кривая 1, при повторяемости один раз в 500 лет; 5 – кривая, полученная с применением выражения (1); между кривыми 4 и 5 показаны кривые, полученные с применением выражения (13) при повторяемости землетрясений 1000, 2500 и 5000 лет. Период приведения принят равным времени ожидания. По оси абсцисс значения в годах отложены по логарифмической шкале (максимальное значение шкалы принято равным T st = 130 лет). Кривая 3 на рис. 4а условно продлена до значения T st = 105 лет для удобства визуализации.

исследований, что не исключает возможности ее практического применения уже сейчас для учета требований пункта 6.19.11 СП 14.13330.2018.

Дефицит сейсмостойкости здания, определяемый путем перехода между расчетными баллами, не может определяться как разность каких-то полученных результатов (оценок). В развитие положений, представленных в монографии [1] и посо- бии СТП 2.13–90 [16], предлагается дефицит сейсмостойкости оценивать как расхождение, непосредственно характеризуемое множителем, определяемым с учетом редуцирования спектра воздействия, которым описывается ожидаемое расчетное землетрясение. Под таким множителем здесь подразумевается коэффициент SF (назначаемый с учетом поправки на возраст здания).