Обоснование графического метода оформления впадин зубьев колеса с несимметричными профилями

Введение. В последние десятилетия в приводах машин начали применяться эвольвентные зубчатые передачи с несимметричными профилями зубьев. Их достоинства достаточно широко исследованы в работах Э.Б. Вулгакова и его учеников [1]. Подобные передачи с большой асимметричностью профилей зубьев могут обладать также свойством самоторможения при обратном ходе (при высоком значении КПД прямого хода). Зубчатые звольвентные колеса для передач с большой асимметричностью профилей зубьев (коэффициент асимметрии 1,5 и более) с необходимой точностью могут быть изготовлены только методами копирования: дисковой фрезой со специальным профилем, литьем, посредством порошковой металлургии и т.д.[2]. Переходные кривые ножек зубьев таких колес не получаются автоматически как при изготовлении обкатным способом, а должны быть специально рассчитаны и воспроизведены на режущем инструменте. Знание этих кривых необходимо для того, чтобы исключить заклинивание передачи при вращении колес, для определения реального коэффициента торцевого перекрытия зубьев передачи (так как в рассматриваемых передачах значительные участки эвольвент на ножках зубьев срезаются переходными кривыми [3]), а также для расчета местных напряжений изгиба в корне зуба. При этом в любой фазе зацепления между несопряженными участками профилей зубьев шестерни и колеса должен обеспечиваться зазор, достаточный для размещения смазки, компенсации неточностей сборки и температурного расширения материала колес. Вопросы конструирования переходных кривых эвольвентных зубьев с большой асимметричностью профилей в известной нам литературе не рассматривались, что затрудняет применение таких передач в технике.

Описание метода и полученные результаты. Рассмотрим пример проектирования зубчатой звольвентной передачи с параметрами: число зубьев z ₁ = z ₂ =6, углы зацепления разноименных профилей a w =20 ° , а W =80 ° , коэффициент асимметрии профилей K= cos а w / cos а W = 5,41. Синтез этой передачи подробно рассмотрен в работе [3]. Схема передачи (торцевое сечение) представлена на рис.1, причем эвольвенты профилей пока не имеют переходных кривых на ножках зубьев. В рабочем режиме ведущее колесо 1 вращается против часовой стрелки, в режиме самоторможения также против часовой стрелки вращается колесо 2.

Для решения поставленной задачи удобно использовать метод обращения движения. Тогда колесо 1 станет неподвижным, а колесо 2 своей начальной окружностью радиусом r_w будет перекатываться по неподвижной начальной окружности радиуса r_{w 1} . Зуб колеса 2 станет занимать определенные положения во впадине зубьев колеса 1, что позволит построить необходимой формы переходную кривую ножек зубьев этого колеса. Таким образом, задача сводится к построению положений зуба колеса 2 в неподвижной системе координат, связанной с колесом 1.

Рис.1. Схема зацепления передачи с параметрами: число зубьев z ₁ = z ₂ =6; углы зацепления рабочего и тормозящего профилей a w =20 ⁰ , а w =80 ⁰

Очевидно, что все точки головки зуба колеса 2 описывают при этом петлеобразные кривые – удлиненные эпициклоиды (удлиненные эпитрохоиды), но более удобно для построений использовать траекторию точки пересечения правого и левого профилей зуба (рис.1, вершина зуба – точка A). Из работы [4] известны параметрические уравнения названной функции, приведенные нами к исходным данным решаемой задачи:

<

x A = ⁽ r w ⁺ r w ₂ ^)C0S Ф^- r a_;

cos

г + г w ₁      w ₂

л

У A = ⁽ r w , ⁺ r w - ₂ ^)sin Ф — r a ₂

sin

V f r w ,

r w ₂

- ф ;

+ г w2

Г

V      ^ww 2

ф, 7

где r_{w 1} , r_{w 2} - радиусы начальных окружностей колес; r_{a 2} - радиус окружности вершин зубьев колеса 2; ф - независимая угловая переменная.

Учитывая, что в решаемой задаче при u=1 r w ₁ = r w ₂ = r w и r a ₁ = r a ₂ = r a , уравнения (1)

можно переписать следующим образом:

<

x_A = 2 r_w cos ф - r_a cos 2 ф ;

_ У A = 2 rw sin ф- Га sin2ф.

Задавая значения ϕ от 0 до 1,56 с шагом 0,05(рад) и составив специальную программу, рассчитаем x_A и y_A по уравнениям (2). Затем построим по этим координатам кривую в осях x и y (рис.2).

Для построения положений зуба колеса 2 удобно воспользоваться шаблоном зуба. Начальное положение шаблона показано на рис.3. Вершина зуба колеса 2 располагается, естественно, на вершине петли траектории; ось симметрии совпадает с межосевой линией O ₁ O ₂ передачи. Далее следует ступенчато перемещать ось колеса 2 на шаблоне по окружности радиуса O ₁ O ₂ в обе стороны от начального положения. При этом вершина зуба – точка A – перемещается по заданной траектории. Установленные положения зуба шаблона очерчиваются. На рис.4 в увеличенном виде показана итоговая картина положений зуба шаблона. Это дает возможность при принятом радиальном зазоре [3] очертить впадину зубьев колеса 1, не пересекая вычерченные положения зуба шаблона. В данном случае для оформления переходной линии использованы дуга окружности и отрезки прямой линии как дающие наиболее технологичные очертания впадины зуба.

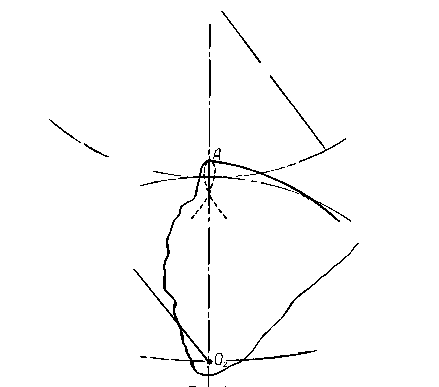
Рис.3. Схема использования шаблона для построения положений зуба колеса 2 (начальное положение)

Рис.2. График траектории точки вершины зуба колеса 2 в системе координат, связанной с колесом 1

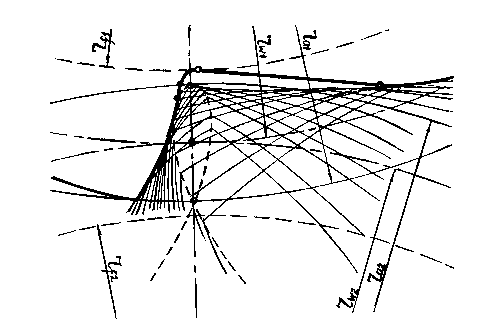
Рис.4. Картина относительных положений зуба колеса 2 и предлагаемая переходная кривая ножек зубьев колеса 1

Положение эвольвентной части зуба колеса 1 определяется как огибающая положений эвольвенты сопряженного зуба колеса 2. Если у зубчатой передачи z ₁ и z ₂ не равны, то описанные построения следует повторить еще один раз для получения переходной кривой ножек зубьев второго колеса.

Выводы

• 1.    Для получения переходных кривых ножек эвольвентных зубьев с большим коэффициентом асимметрии необходимо построить относительные положения зубьев сопряженного с ним колеса. Вершина этого зуба в относительном движении перемещается по удлиненной эпициклоиде.

• 2.    Переходная кривая ножек зубьев строится с необходимым зазором относительно положений зуба сопряженного с ним второго колеса. Для этого при принятом радиальном зазоре рекомендуется использовать наиболее технологичные геометрические элементы: дуги окружностей, отрезки прямых и т.п.