Обоснование инженерных методов идентификации режимов оптимизации асинхронных электроприводов

Асинхронные электроприводы с частотным регулированием широко применяются в самых различных областях современной промышленности и в энергетике. Примерами могут быть металлургия и металлообрабатывающая промышленность, нефтегазовая отрасль, горнодобывающая промышленность и многие другие. При проектировании электроприводов, как правило, мощность электродвигателя и преобразователя частоты выбирается с некоторым «запасом» (15–20 %), который при уточнении технологических особенностей работы механизмов возрастает до 25–30 %. Система регулирования скорости вращения двигателей с преобразователями частоты легко обеспечивает необходимую скорость, но при этом значения токов статора, потребляемой реактивной мощности и активных потерь в электродвигателях и кабелях остаются значительными и снижают показатели эффективности механизмов и их технико-экономические характеристики. Известны методы оптимизации энергопотребления в таких приводах снижением амплитуды статорного напряжения при сохранении его частоты. В последние годы подобная функция заложена в алгоритмы стандартных ПЧ, и реальные режимы работы электроприводов различных общепромышленных механизмов – насосов, вентиляторов, транспортных механизмов – подтверждают эффективность алгоритмов. Однако при описании этих алгоритмов [1–6] основное внимание уделяется снижению амплитуд статорных токов и недостаточно подробно рассматриваются изменения скорости вращения, скольжения и амплитуды токов ротора, что делает этот режим «оптимизации» не слишком понятным. Применяемые для анализа режима работы привода традиционные схемы замещения и векторные диаграммы [5–7] не позволяют дать представление о характере процессов в асинхронных электроприводах при подобной коррекции. В частности, не слишком ясно, до каких значений можно снижать напряжение. Известны случаи из практики, когда снижение напряжения при сниженных токах статора приводило к выходу двигателей из строя.

В ходе проведенных авторами статьи исследований была решена следующая задача: предложены инженерные методы идентификации режима оптимизации процессов в асинхронных частотнорегулируемых электроприводах и сформулированы положения, которые позволили показать особенности работы частотно-регулируемого привода с пониженной амплитудой статорного напряжения и, соответственно, сниженным значением основного магнитного потока, определяемого отношением амплитуды напряжения, подаваемого на статор двигателя к его частоте.

Постановка задачи

Очень часто важнейшей проблемой приводов общепромышленных механизмов становится не поддержание скорости вращения с высокой точностью, а снижение энергопотребления привода при некотором снижении скорости вращения и увеличении скольжения в асинхронном двигателе. При этом реальная нагрузка электропривода может изменяться из-за производственных, технологических или экономических причин на длительные временные периоды: несколько недель или месяцев. В эти периоды загрузка электропривода может существенно изменяться. И даже при очень точном исходном выборе, мощность электродвигателя и оборудования может стать достаточно далекой от оптимальной.

Особенно часто такие задачи возникают в добывающих отраслях на электроприводах погружных насосов, которые работают с загрузкой существенно ниже номинальной. Известно, что в таких приводах в статорных токах преобладают реактивные составляющие, которые снижаются при уменьшении амплитуд статорного напряжения, почти не влияя на скорость вращения двигателя. В ряде преобразователей частоты и устройствах мягкого пуска [8] предусмотрен режим экономии мощности, при котором происходит автоматическое снижение амплитуды статорного напряжения.

В ряде научных статей эта коррекция достаточно подробно описана как способ снижения реактивной мощности, снижения статорных токов и связанных с этим снижением активных потерь в двигателях и кабелях (которые для погружных насосов представляют существенные значения). Однако явно недостаточно описаний данного режима работы асинхронного электродвигателя с комплексной точки зрения, то есть недостаточно четко описываются процессы изменения токов статора и ротора, скольжения, формирования электромагнитного момента и «поведение» механической характеристики двигателя.

Одной из проблем, мешающей такому описанию, приходится считать традиционные методы рассмотрения асинхронных электродвигателей и процессов в них – это схемы замещения, векторные диаграммы и механические характеристики [4–7].

Следует отметить, что эти методы описывают изменения амплитуды напряжения на статоре несложными, но громоздкими математическими выкладками, зависящими от конкретных параметров электродвигателей – активных и индуктивных сопротивлений статора и ротора и не дающими четкого представления о характере процессов.

Предлагаемые ранее изменения схем замещения [9, 10] также не позволяют получить наглядные результаты. Рассмотрим эти положения подробнее.

Теоретическая часть

До настоящего времени наиболее применяемым аппаратом остаются схемы замещения и векторные диаграммы и механические характеристи- ки. Исходно эти методы применяются для расчётов процессов изменения токов i. и /2 при постоянных ист, f, нагрузке (скольжение s).

При создании алгоритмов частотного регулирования асинхронных электроприводов одной из главных задач и при векторных способах управления, и при скалярных – это линеаризация асинхронного электродвигателя и стабилизация основного магнитного потока, пропорционального отношению U/f на уровне номинального. Поэтому алгоритм снижения амплитуды напряжения при неизменной частоте, уменьшающий основной магнитный поток в двигателе, принимается чем-то «эмпирическим», полученным из практического опыта.

Не вызывает сомнения и другая особенность асинхронного привода – при нагрузке, близкой к номинальной, снижение напряжения вызывает рост статорного тока. Объяснения, как эти противоположные тенденции реализуются одной, практически линейной схемой замещения, очень трудно найти в работах по частотному управлению асинхронными электродвигателями[6–9]

Наиболее часто для анализа статических режимов работы используют Т-образную и Г-образную схемы замещения асинхронного электродвигателя . На рис. 1 приведены схемы в качестве цитаты из книги А.А. Усольцева [10].

Векторные диаграммы, которые описывают установившиеся режимы, связывают между собой векторы токов цепей намагничивания, ротора и статора, типовая диаграмма приведена на рис. 1c, взята из той же книги А.А. Усольцева [10]

Следует обратить внимание на то, что в схемах присутствуют только по одному нелинейному элементу – это активные сопротивления ротора R ₂. Поскольку при работе двигателя в установившемся

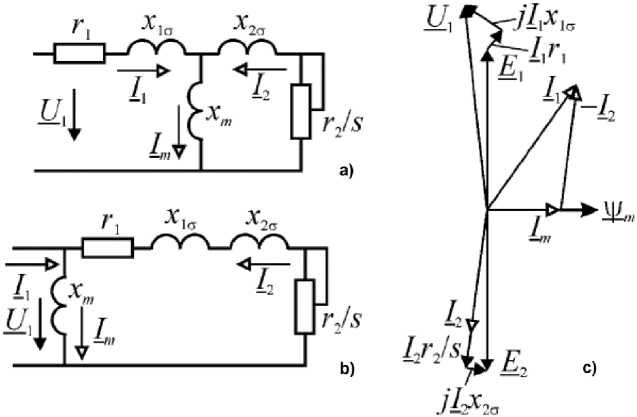
Рис. 1. Схемы замещения (Т-образная (а); Г-образная (b)) и векторная диаграмма асинхронного электродвигателя (c)

Fig. 1. Equivalent circuits (T-shaped (a); L-shaped (b)) and vector diagram of an asynchronous electric motor (c)

режиме сколь ж ен и е обы чн о ме няе тся о т 0 , 0 1 д о 0 , 1 , им е н н о э т и и зме нения с т а н ов я тс я наиболее в ажным фа кт ором в форм иро вании токов д в и г а т еля.

Рас чет т о к о в с т ат о ра и р отора п о э т ой с х ем е дос т аточно г ром оздкая оп ерац и я , как сл еду ет из форм ул ы той ж е м он ог раф и и , да ж е д ля упрощенной Г- обра зно й с х е мы ток р от ора будет о пре д еляться по формуле

I                                        ' •

JfeZ+^Z)Mri+^^

Причем скольжение s д ол жно оп ред ел я ть ся п о форм ул е Кл осс а, к о т ора я даж е в п рост о м в ари а н т е представляет собой нелинейную ф у н к цию :

2М г+?

Не о бхо димо о б р а т и ть вн и ман и е, ч то в Г -образ- ной сх ем е з а ме щ ен и я ц еп ь н а ма г ни ч и ван ия не св я зана с не ли н е й н ой ц е п ь ю , п ара м ет ры кот о рой за ви с ят от н аг р уз ки ( цепь рот ора ). Э то оз н ача ет , что связь эта не имеет с у щес тв ен н ог о з н ач ения, ос о бенно дл я с тати че ског о режим а ра бот ы. О чен ь час т о при рас четах р еж и мов рабо т ы при в ода с час т отным у пра в ле н ием п р ен ебре г аю т в е кторам и с ма л ым и а м пли ту да ми, н а при м ер па де н ие м напряжения в роторных цепях [12– 15].

Очевидно, что для инж енерн ых рас чет о в до п уст и мо про ве ст и у п рощ е н и я при в е де н н ы х в ы ше форм ул и зав исим остей , ко т ор ые н е н ару шили бы наиболее важных взаимосвязей.

О братим вним ани е на ве к торную диа г рам му на рис. 1c, пр опо рции м е ж ду д л и н ам и в ек т о ров U ₁ и ^ i • х_1а; Л • ^ri ; ^₂ • х_2а отражаю т на и бо л ее часто вс т ре чаю щие с я соотношени я м е ж д у амп лит у дами т оков и в е кт оро в пад е н и й напр я же н и й .

Векторы 1 1 • х_1а; 1 1 • r₁; 1'₂ • х_{2 с} существенно меньше векторов U 1 , 1₂ •—.

« 1

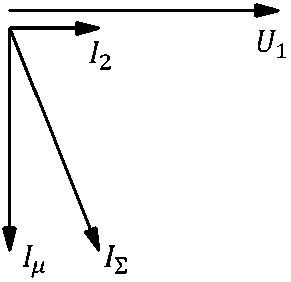
Если векторами 4 • х_1а; 1 1 • г₁; 1 ^ • х_2а пренеб речь, то диа г рам м а п ри мет вид к ак на ри с. 2 b.

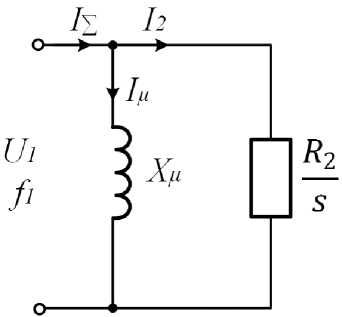
Э т а д иаг р амм а бу д ет соо тв е т с тв ов ат ь с хем е замещения, приведенной на рис. 2а. В это й с х еме, к ак в

Г-образной, магнитный поток определяется только реактивными параметрами и не зависит от скольжения. А роторный ток, который является практически полностью активным, определяется только нелиней- ным активным сопротивлением ротора, которое пол- ностью определяется скольжением s.

Известно, что для линейного участка механической характеристики формула Клосса (упрощенная формула) может быть еще упрощена. Схе- ме соответствует механическая характеристика, которая рассчитывается по формуле Клосса:

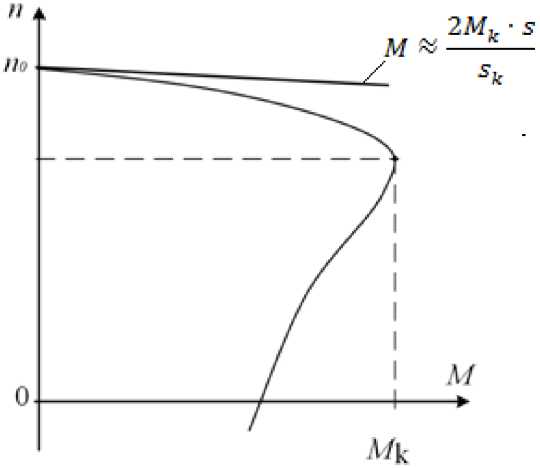
«=В- sk s

где Мk – критический момент; sk – критическое скольжение; s – скольжение.

Характеристика представлена на рис.3а.

Поскольку для участка механической характеристики от 0 до s_н выполняется условие s ^ 0 , s_k » s, формула Клосса может быть представлена с достаточной точностью в следующем виде:

м^^м^ ^s । ^sk ^sk ^s

2M^s « к

Эта формула и соответствующая ей механическая характеристика (рис. 3b) интерпретируют электродвигатель, в котором развиваемый момент пропорционален скольжению, то есть отставанию скорости вращения n электродвигателя от синхронной скорости n0, которая является и скоростью холостого хода.

Такие зависимости характерны для двигателей с независимым формированием взаимодействующих магнитных потоков, и это дает основание считать предложенную в статье схему замещения двигателя и векторную диаграмму достаточно обоснованной, то есть именно двигателя со схемой замещения, представленной на рис. 2а.

Предлагаемые упрощённые схемы замещения, векторная диаграмма и механическая характеристика наглядно покажут, как изменения U₁ влияют на все координаты электродвигателя, в первую очередь токи ротора и статора.

а)

b)

Рис. 2. Упрощенная схема замещения (а) и упрощенная векторная диаграмма асинхронного электродвигателя (b) ( 7 ц - ток намагничивания; 7 ₂ - суммарный ток; 1₂ - ток ротора)

Fig. 2. Simplified equivalent circuit (a) and simplified vector diagram of an asynchronous motor (b)

( 7 _ц - magnetizing current; 7 ₂ - total current; 7 ₂ - rotor current)

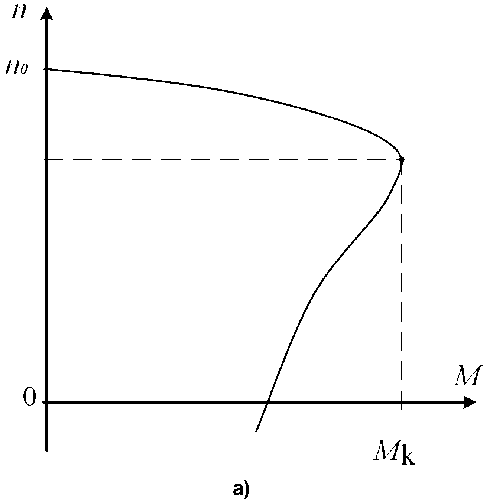
Рис. 3. Механическая характеристика асинхронного двигателя (а), линеаризованная на рабочем участке механическая характеристика (b) Fig. 3. Mechanical characteristic of an asynchronous motor (a), linearized mechanical characteristic in the working area (b)

Вывод аналитических зависимостей

К а к извес т н о , к ри ти ч еск ий м о ме нт М_k пропорционален U ^ , то гда и з фо рм у лы (2) с л едует, что в к онк рет ном ре ж и м е с ко л ьже н и е будет об-

ратно про п о рциона л ь н о к р и тиче с к ому с к ольже-

н ию ил и к ва дра ту а м плит уд ы н апряжен ия , пода-

в а емому н а ст а т о р асин х ронн о го э л ек тродв иг ател я :

М^к   1

---~ —т. 2М к   U ?

Как следует из схе мы зам е щени я (см. рис. 2а), реактивный ток – ток нам а г н ич ива ни я , про т е к а ю щ и й ч ер ез линей н у ю и нд ук тивн у ю це п ь, об раз ованную Х_ц, определяется форм ул ой

' и

U i ^хн

То к ротора, а к т и вный ток , п ро т е к ае т ч ер ез ак-

т ив ную це пь , нел ине йно е с опр оти в лен ие ротор а,

зависящее от s ^

« 2

S

^ 2

U i -S    1

Г 2    U i

Эта зависимость отмечается в работе [7] без каких-либо дальнейших выводов. То есть по отношению к изменению U ₁ активный и реактивный токи в асинхронном электродвигателе имеют противоположные тенденции: реактивный ток пропорционален амплитуде статорного напряжения '₁~U₁, а активный обратно пропорционален этой амплитуде:

V^U1 ; ' 2— .

Суммарный ток образован векторным суммированием тока намагничивания и роторного токов:

141 = ^ГЫМ2-

Эти тенденции сохраняются при любых нагрузках (при любых скольжениях s ), только при малых нагрузках (s ^ 0) /₂ активный ток существенно меньше реактивного, суммарный ток близок к реактивному и почти пропорционален амплитуде напряжения (рис. 4):

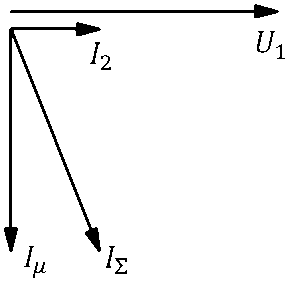
Рис. 4. Упрощенная векторная диаграмма асинхронного электродвигателя при малой активной нагрузке ( 1 _Ц - ток намагничивания; 1 ^ - суммарный ток; 1₂ - ток ротора)

Fig. 4. Simplified vector diagram of an induction motor with a small active load ( 1 ^ - magnetizing current; 1 ^ - total current; 1 ₂ - rotor current)

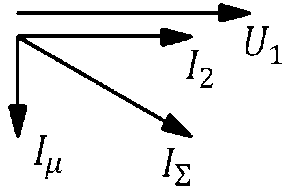
Рис. 5. Упрощенная векторная диаграмма асинхронного электродвигателя при большой активной нагрузке ( 1 ^ - ток намагничивания; 1 ^ - суммарный ток; 1 ₂ - ток ротора)

Fig. 5. Simplified vector diagram of an induction motor with a heavy active load ( 1 ^ - magnetizing current; 1 ^ - total current; 1 ₂ - rotor current)

• I ^ ~U 1 ; h-- ; h:*^ ,

а при значительной нагрузке преобладает активный ток, и суммарный ток становится близок к обратно пропорциональной величине по отношению к амплитуде статорного напряжения (рис. 5):

• ^ i ^- , ⁱy ^> ^ 2 ^T , i s ~ i i .

При оптимизации привода с малой нагрузкой по мере уменьшения U_i возрастает ток ротора, по большей части активный. Если нагрузка становится значительной, суммарный ток определяется активной составляющей и возрастает при снижении напряжения на статоре, то есть предложенная схема замещения достаточно наглядно описывает процессы в двигателе как при малой активной, так и при значительной нагрузках.

То есть предложенная схема замещения с независимыми каналами управления активными (роторными) токами и токами намагничивания (реактивными) отражает взаимосвязи между тенденциями изменения токов ротора и статора при уменьшении амплитуды статорного напряжения и нагрузкой привода, которая характеризуется скольжением, дополняя исследования асинхронных электроприводов, проведенные ранее [16, 17].

Полный статорный ток /_Е при малой нагрузке уменьшается при снижении напряжения U ₁ за счет уменьшения преобладающего реактивного тока I _μ (тока намагничивания), а при большой нагрузке снижение напряжения вызывает рост суммарного статорного тока за счет роста преобладающего активного тока I 2 (тока ротора).

Можно ли в частотно-регулируемом приводе с низким магнитным потоком экономить активную мощность

Предложенная упрощенная схема замещения очень наглядно и с достаточной точностью интерпретирует особенности частотного регулирования с изменением основного магнитного потока в двигателе – отношения U/f .

Схема замещения и вытекающие из нее векторная диаграмма, упрощенная формула Клосса и механическая характеристика позволяют установить четкие взаимосвязи между амплитудой статорного напряжения, критическим моментом, скольжением, нелинейным сопротивлением ротора в схеме замещения и роторным током. Параллельная интерпретация цепей намагничивания и роторной цепи с активными процессами позволяет показать механизм изменения активного и реактивного токов в двигателе при изменении амплитуды статорного напряжения.

Предложенный аппарат показывает, что изменение напряжения на статоре вызывает пропорциональное изменение реактивного тока или тока намагничивания и обратно пропорциональное активного или роторного тока.

В исходной схеме замещения (см. рис. 1) и в реальных электродвигателях процессы аналогичны. Упрощенный аппарат, предложенный в статье, только делает эти тенденции более наглядными.

Отсюда следует, что уменьшение напряжения в первую очередь существенно уменьшает реактивную мощность, уменьшается и полный ток двигателя, который образуется векторной суммой токов. Его снижение уменьшает активные потери в силовых кабелях, которые весьма ощутимы для ряда промышленных объектов.

Таким образом, предложенная схема замещения (см. рис. 2) позволяет получить очень наглядно и быстро результаты, полностью идентичные результатам экспериментов, испытаний и практике.

Из этой схемы следует, что снижение амплитуды напряжения позволяет снизить реактивный ток и увеличивает активный ток ротора. При этом существенным оказывается и снижение полного тока статора двигателя.

Снижение амплитуды статорных напряжений увеличивает скольжение и уменьшает активные мощности асинхронных двигателей. Важно учитывать, чтобы это снижение не влияло на технологические показатели агрегатов, управляемых оптимизируемыми электроприводами. Снижение полных токов статоров асинхронных электродвигателей – особенно важный результат для электроприводов с длинными кабелями электропитания – например, для глубинных насосов нефтедобывающих агрегатов, имеющих кабели длиной 200–600 м.

Заключение

Предложенная схема замещения, несмотря на допущения, очень хорошо интерпретирует частотное регулирование с ослабленным основным магнитным потоком, описывает процессы изменения основных переменных в АД при изменении отношения амплитуды напряжения на статоре к его частоте и позволяет четко разделить процессы формирования активного и реактивного токов, их влияние на суммарный ток и показать возможности метода коррекции и его последствия для скольжения, скорости и производительности. Схема замещения и соответствующие ей векторная диаграмма и формула Клосса могут эффективно использоваться при инженерных расчетах основных параметров оптимизированных по мощности режимов работы частотно-регулируемых электроприводов. Это позволит существенно расширить возможности и улучшить эффективность бездат-чиковых систем управления асинхронных электроприводов по сравнению с существующими [18, 19].