Обоснование использования физической модели материальной точки при исследовании кинематических характеристик автомобильного транспортного средства при косом наезде на боковые тросовые ограждения

Введение . Системы безопасности, предназначенные для организации транспортных потоков на дорожных трассах, способствуют минимизации неблагоприятных последствий дорожно-транспортных происшествий (ДТП). В настоящее время приобретают популярность тросовые дорожные ограждения, которые устанавливаются на разделительной полосе автомобильных дорог для предотвращения преднамеренных и непреднамеренных переездов транспортных средств через дорогу, а также на обочинах — для предотвращения выездов транспортных средств за пределы автомобильной дороги 1 .

Различные конструкции тросовых ограждений состоят из общих элементов: тросов, стоек, анкерных блоков, стяжных устройств, но разнятся по типу их монтажа 2 [1–4], в частности, по способу крепления тросов (рис. 1), что существенно влияет на формирование математических моделей. Также различно поведение стоек при наезде АТС. Стойки могут сминаться либо, выходя из гильз, компоноваться одна с другой и обеспечивать таким образом дополнительное торможение АТС [5].

Столкновение автомобиля с тросовым ограждением характеризуются сложной механикой взаимодействия, т. к. тросы обладают высокой степенью геометрической нелинейности, а стойки и грунт — высокой степенью физической нелинейности, при этом почти все процессы являются переходными [5].

Рис. 1. Некоторые виды стоек тросовых ограждений [6]

Механика

1 Отраслевой дорожный методический документ ОДМ 218.6.017–2015. Методические рекомендации по применению дорожных ограждений различного типа на автомобильных дорогах федерального значения / рекомендован распоряжением Федерального дорожного агентства от 23.12.2015 № 2489-р. URL: (дата обращения: 08.01.2021).

• ² Horne DA. Report 350 Acceptance of New York Three-Strand Cable Terminal. Office of Highway Safety Infrastructure, FHWA, U.S. Department of Transportation – Washington, D.C.; February 14, 2000. Available from: https://highways.dot.gov/ (accessed: 21.01.2019).

Для определения траектории АТС можно использовать уравнения колебаний струны, используемые в аналитических расчетах аэрофинишеров 1, 2 и вантовых конструкций 3, 4 . Но в связи со сложностью конструкции ограждений возникают сложности формулировки краевых условий. Энергетические методы также дают набор уравнений, которые не решаются аналитически 5 [7]. Все это приводит к необходимости исследования ограждений с помощью инженерных пакетов прикладных программ как для моделирования самого тросового ограждения, так и системы краш-теста. При этом часто используется численный метод конечных элементов в явной постановке, реализуемый в программных комплексах LS-DYNA, MARC, NASTRAN и др. [5, 8, 9].

Недостатками построения КЭ-моделей являются: сложность разработки; длительность периода расчета (120 ч. и более); необходимость проверки правильности построения. Таким образом, период подготовки основы для исследования является довольно длительным. В связи с этим предложен метод приближенного аналитического расчета движения АТС по данным натурных испытаний, основанный на методах теоретической механики. Аналитический расчет позволяет проверить правильность разработанной КЭ-модели, а также сократить время исследования пассивной безопасности в 2–3 раза, поскольку для анализа пассивной безопасности уже нет необходимости строить КЭ-модель самого тросового ограждения, а использовать аналитически полученные перемещения.

Материалы и методы. В результате наблюдения за АТС в процессе натурных краш-тестов была выдвинута гипотеза: при наезде на боковые тросовые ограждения АТС можно представить как твердое тело, совершающее поступательное движение (рис. 2).

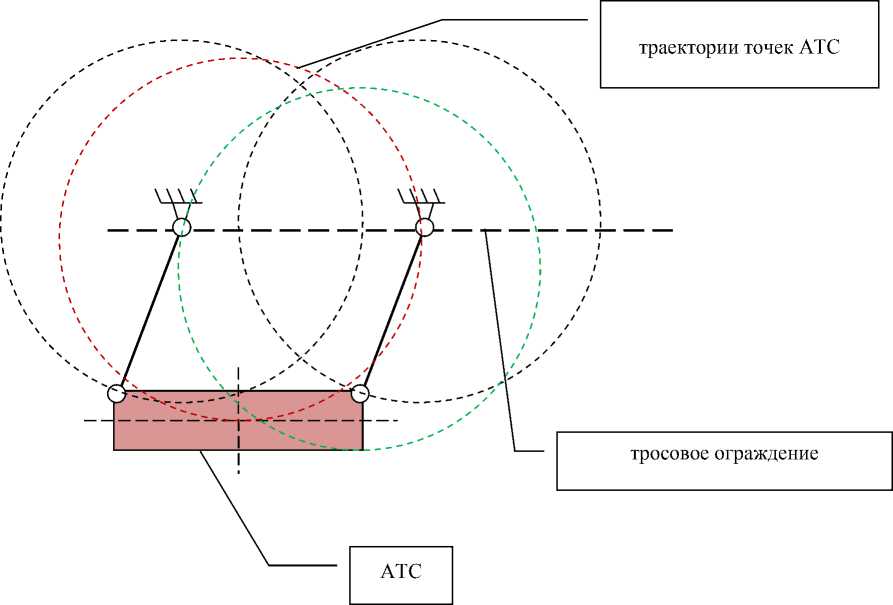
Рис. 2. Модель АТС как твердого тела, совершающего поступательное движение

Кроме того, делается ряд фундаментальных предположений о динамике АТС во время ДТП, обосновывающих использование предложенных теоретико-механических моделей явления:

• •    боковые и продольные замедления транспортного средства постоянны в течение интервала времени, необходимого для ориентации АТС параллельно недеформированному барьеру;

• •    вертикальные и вращательные ускорения автомобиля игнорируются;

• 1    Нуралиева А. Б. О динамике троса космического лифта : автореф. дис. … к - та физ. - мат. наук. М., 2012. 20 с.

• 2    Михайлюк Д. С. Конечно - элементное моделирование и исследование динамики палубного аэрофинишера : автореф. дис. … к - та техн. наук. СПб., 2009. 19 с.

• 3    Дядькин С. Н. Обоснование, технология навесной сборки и мониторинг байтовых пролетных строений мостов с учетом климатических факторов (на примере моста через реку Обь у г. Сургута) : автореф. дис. … к - та техн. наук. Волгоград, 2005. 20 с.

• 4    Ле Тху Хыонг Оптимизация параметров пролетных строений висячих мостов, усиленных и не усиленных наклонными вантами, при их проектировании с применением ПК : автореф. дис. … к - та техн. наук. М., 199 9. 25 с.

• 5    Лось М. В. Численное моделирование поведения системы «тело - трос» с учетом изгибной жесткости троса и механизм петлеобразования : автореф. дисс. … к - та физ. - мат. наук. М., 2000. 19 с.

• •    боковая составляющая скорости равна нулю после того, как транспортное средство перенаправлено параллельно перилам ограждения;

• •    поскольку транспортное средство перенаправляется, оно не входит в зацепление с перилами ограждения;

• •    деформация транспортного средства происходит в зоне удара, но положение его центра масс существенно не изменяется;

• •    центр масс автомобиля движется так, как будто вся его масса сосредоточена в этой точке;

• •    барьер может быть жестким или гибким;

• •    силы трения шин автомобиля о поверхность проезжей части игнорируются;

• •    система ограждений не содержит разрывов, которые могут привести к резким вертикальным движениям автомобиля.

При таком представлении движения автомобильное транспортное средство (рис. 3) возможно рассматривать как материальную точку некоторой массы m [10]. Начало отсчета декартовой системы координат соответствует точке начала контакта транспортного средства и ограждения. Движение материальной точки начинается со скоростью 5 0 , направленной под углом а к плоскости ограждения (оси x ) [6].

У*

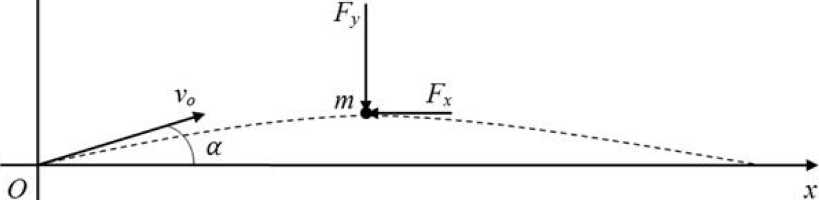
Рис. 3. Расчетная схема АТС [6]

Противодействие движению  транспортного средства  со стороны тросового ограждения моделировалось силами [6]:

• •    при боковом отклонение вдоль оси y — силой упругости P_y = - ky и диссипативным сопротивлением Py^uc = - by , то есть F_y = — ky — by ;

• •    сопротивление движению вдоль оси x — силой трения F_x = — fN I , где N I — сила инерционного давления, то есть N I = my [6].

В результате движение АТС описывается системой дифференциальных уравнений [6, 11]:

• x = - fy ;

y + 2 e y + p² y = 0.

Решением системы являются перемещения в функции времени t :

x ( t ) = — fy ( t ) + v ₀ ( cos a + f sin a ) t ;

'            ₍ . v _n sin a .

y (t ) = -0——e sin pt.

В [6] доказано, что сила трения Кулона со стороны дорожного ограждения не оказывает существенного влияния на моделируемое движение АТС. Физическое моделирование АТС как материальной точки не является новым при исследовании наезда на боковые ограждения. Такой подход был применен Р. М. Олсоном, Э. Р. Постом и Ф. Ф. Макфарландом при описании наезда автомобиля на жёсткие ограждения мостов [12]. Здесь расчет сопротивления бокового ограждения базировался только на классической модели трения Амонтона-Кулона.

Механика

В отличие от этой задачи характер взаимодействия АТС и ограждения в настоящей работе описан принципиально новой моделью. При внешней похожести постановки задачи физическая сущность взаимодействия АТС и ограждения качественно отличается от сущности взаимодействия с более жесткими ограждениями. В настоящей работе это было учтено посредством силовых моделей Амонтона-Кулона с учетом силы инерционного нормального давления и модели сопротивления Кельвина-Фойхта.

Также, в контексте исследования характера наезда на тросовые ограждения следует отметить работу M. B. Bateman и др. [9]. Данные натурных испытаний, представленных в этой работе, явственно демонстрируют, что при косом наезде на тросовые ограждения движение АТС близко к поступательному, когда угол рыскания не превышает 10°. Здесь процесс наезда описан двумя моделями:

• 1.    Простая динамическая модель транспортного средства, где использовался метод Рунге-Кутта четвертого порядка для численного решения дифференциального уравнения движения АТС. При этом учитываются силы воздействия со стороны ограждения (натяжение троса) и дороги (сила трения по классической модели Амонтона-Кулона). Во время удара полагается, что колеса не требуют рулевого управления.

• 2.    Квазистатическая модель ограждения, которая предназначена для расчета изменения напряженности тросов при изменении их геометрии в результате движения автомобиля.

В результате расчетная модель получилась достаточно громоздкой и требует численного решения, тогда как модель, предложенная в настоящей работе, предусматривает алгоритмы расчета, легко проводимые аналитически без применений численных методов.

Приближенный аналитический расчет кинематических характеристик АТС. В результате сделанных предположений получен алгоритм построения перемещения АТС, названный гармоническим [6]. Далее предложены квадратичный и кубический алгоритмы, основанные на построении полиномных функций перемещений [13]. Здесь противодействие движению АТС со стороны тросового ограждения вдоль оси y определяется некоторой функцией P_y(t), в результате интегрирования которой функция перемещения АТС вдоль оси y имеет характер полинома второго, либо третьего порядка. Моделирование сопротивления движению вдоль оси x осталось прежним.

Проведем сравнительный анализ результатов приближенного аналитического расчета кинематических характеристик АТС. На рис. 4-6 представлены расчетные данные для автобуса Мерседес-Бенц-0345. При построении перемещений АТС использовались данные натурных испытаний Государственного научного центра РФ ФГУП «НАМИ».

y, м

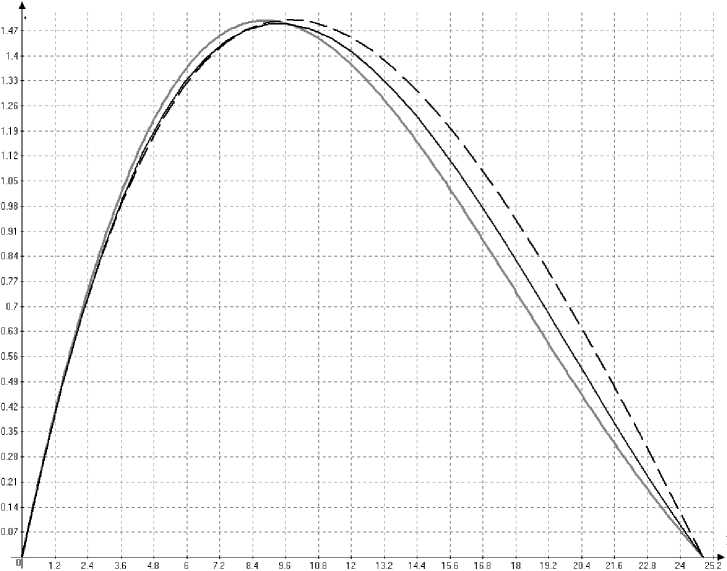
х, м

Рис. 4. Взаимозависимость отклонений x , м и у , м, рассчитанных методами: кубического приближения — черная сплошная линия; квадратичного приближения — пунктирная линия; гармонического приближения — серая линия [13]

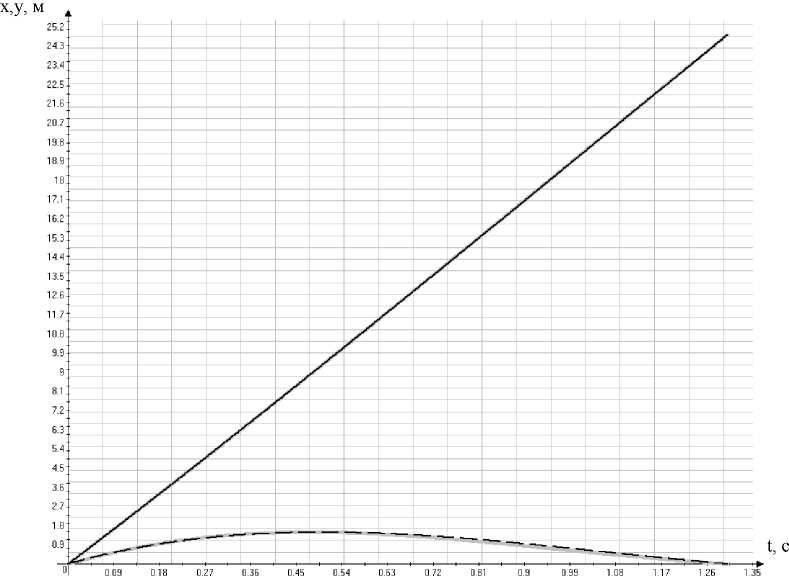
Рис. 6. Зависимости отклонений x , м и y , м от времени t , c, рассчитанные методами кубического и гармонического приближения вдоль оси x — сплошная черная линия; вдоль оси y : пунктирная линия — методом кубического приближения, серая линия — методом гармонического приближения [13]

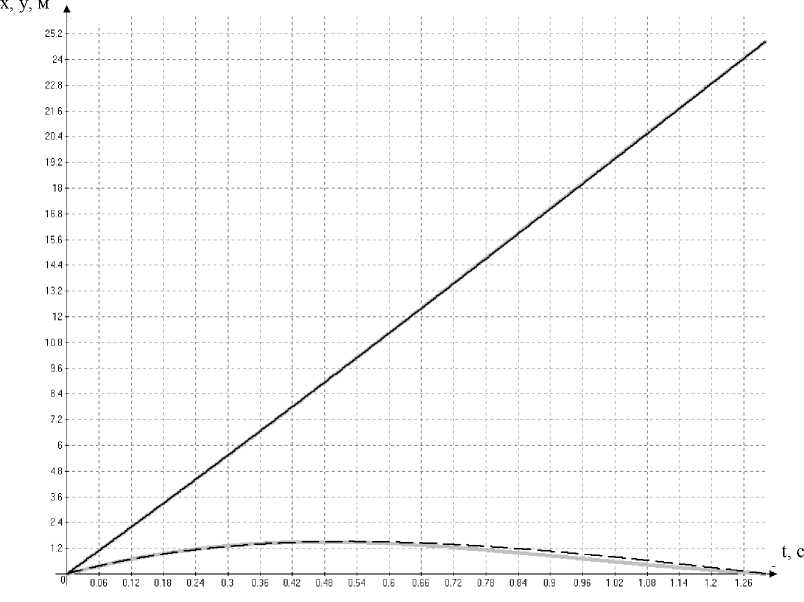
Рис. 5. Зависимости отклонений x , м и y , м, от времени t , c, рассчитанные методами квадратичного и гармонического приближения вдоль оси x — сплошная черная линия; вдоль оси y : пунктирная линия — методом квадратичного приближения, серая линия — методом гармонического приближения [13]

Как видно из приведенных расчетных данных, расходимость аналитических методов между собой не превышает 20 %. Такие же вычисления были проведены и для автомобиля ГАЗ-3102 [12].

Механика

Построение конечно-элементной модели контакта тросового ограждения и автобуса Мерседес-Бенц-0345. Для анализа эффективности приближенного метода построения траектории движения АТС разработана КЭ-модель взаимодействия тросового ограждения и автобуса Мерседес-Бенц-0345 в соответствии со стандартом организации СТО 521000-005-10690827-20151, согласованным с Росавтодором в 2017 г. Согласно этому стандарту проводился монтаж тросовых ограждений для испытаний, результаты которых также были использованы при аналитическом моделировании траекторий и отклонений АТС. Объектом виртуальных испытаний были тросовые ограждения марки 14ДД/У4(300)-П-1, 1-3, 0-ГБ [11, 13] с параметрами:

• •    гильзы восьмигранные марки ГЗ 500/У;

• •    стойки СТД-2 состоят из двух элементов в виде квадратной трубы длиной 1500 м с размерами поперечного сечения 50×50×3 мм;

• •    шаг стоек с забетонированными гильзами на рабочем участке — 3 м;

• •    шаг на начальном и конечном участках — 2 м;

• •    высота стоек над поверхностью дорожного полотна — 1,1 м.

Параметры троса:

• •    трехпрядный, семижильный;

• •    диаметр — 19 мм;

• •    расчетное разрывное усилие ≈ 173 кН;

• •    количество ветвей — 4.

Параметры автобуса Мерседес-Бенц-0345 [12, 13]:

• •    полная масса — 14050 кг;

• •    габаритная длина — 12000 мм;

• •    габаритная ширина — 2500 мм.

Скорость вхождения АТС в контакт с ограждением — 69 км/ч. Угол между плоскостью ограждения и направлением движения АТС — 20º в соответствии с методикой ГОСТ Р 52721—2007 (пп. 6.1–6.6) [11, 13]. Покадровые изображения АТС по данным натурного 2 и виртуального испытаний представлены в таблице 1.

Таблица 1

Сравнительные покадровые изображения АТС

• ¹    СТО 521000 -005- 10690827―2015. Ограждения удерживающие боковые барьерного типа для автомобилей с применением секции балки из «с - образного» профиля / Предприятие «ПИК» // rosavtodor.gov.ru URL: https://rosavtodor.gov.ru/storage/app/media/rosavtodor/b/2016/02/09/sto_521000_005_10690827_2015.pdf (дата обращения: 10.01.2021) .

• ²    СТО 10690827 - 001―2015 Ограждения дорожные удерживающие боковые деформируемые, тросового типа. Технические условия / Предприятие «ПИК» // rosavtodor.ruwwwrosavtodor.ru URL: http://rosavtodor.ruwww.rosavtodor.ru/storage/app/media/uploaded-files/sto-10690827-001-2015.pdf (дата обращения: 08.01.2021).

  Момент времени t , с

  
  

  натурные

  
  

  0,32

  
  

  0,48

  
  

  0,64

  
  

  0,80

  
  

  0,96

  
  

  1,12

  
  

  Вид испытаний

  
  

  виртуальные

  
  
  
  
  
  
  
  

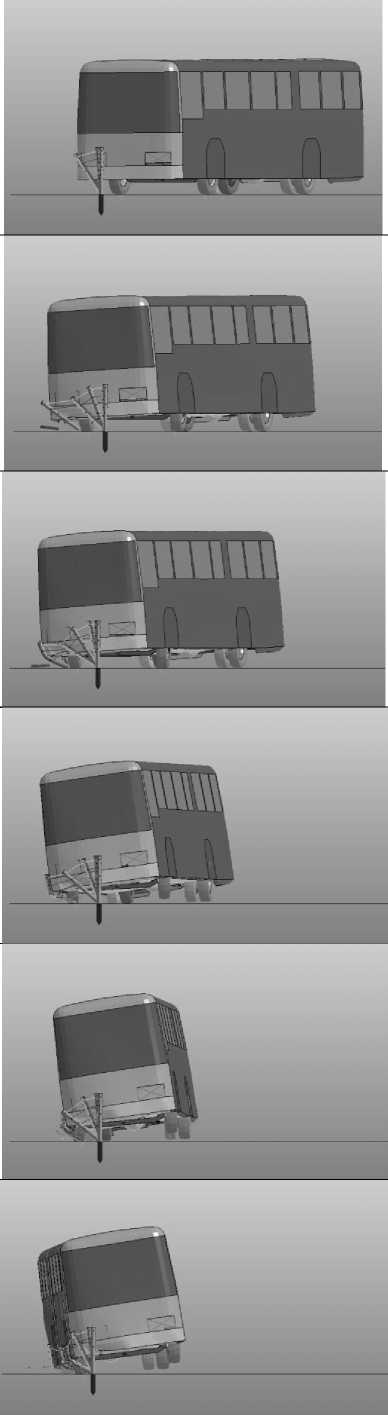
  Механика

  
  

Результаты натурных испытаний практически совпали с результатами виртуальных испытаний, т. к. в обоих случаях динамический прогиб ограждения составил 1,5 м; длина пути взаимодействия АТС с ограждением по расчету — 23,5 м, по результатам натурных испытаний — 25 м. Относительная погрешность по длине пути взаимодействия АТС с ограждением не превысила 6 %.

Результаты исследования. В результате виртуального испытания с использованием разработанной КЭ-модели тросового ограждения определены траектории характерных точек автобуса Мерседес-Бенц-0345. На рис. 7 отмечены точки АТС, для которых снимались показания, точка С соответствует центру тяжести.

x,y, мм

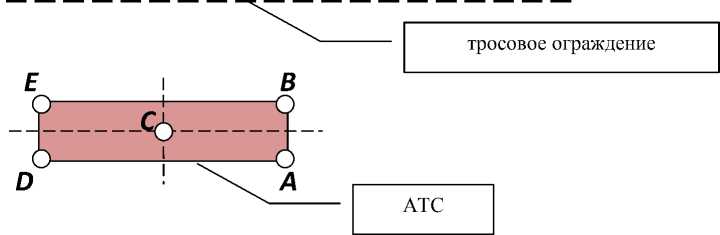
Рис. 7. Выбранные для анализа точки АТС: A , B — на лобовой поверхности; D, E — на задней поверхности

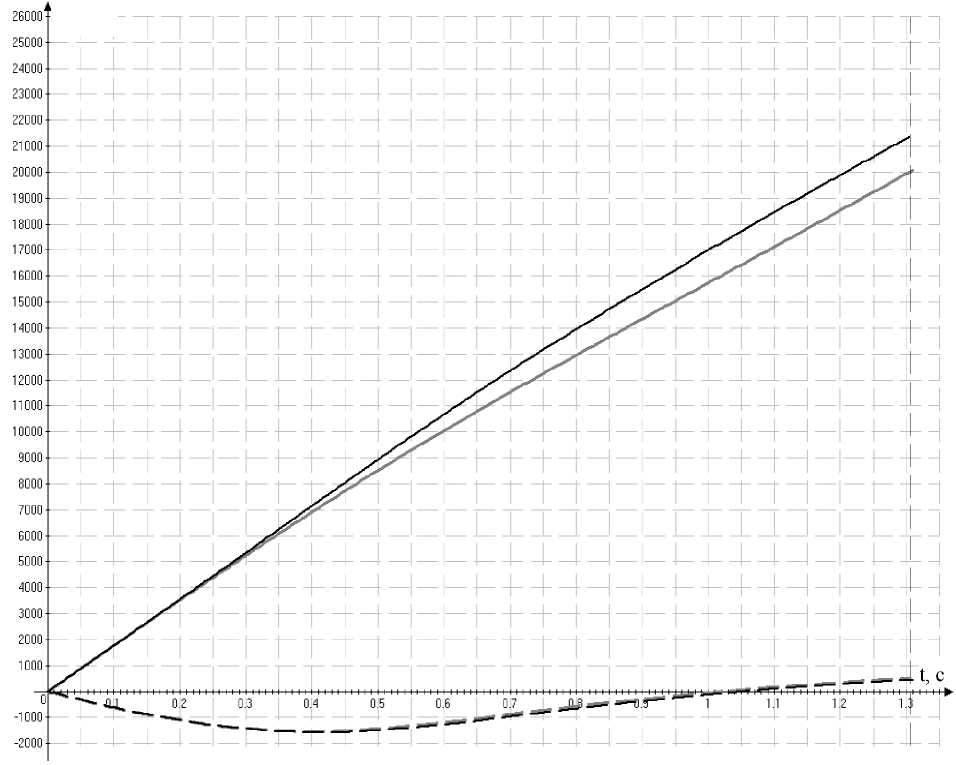
Рис. 8. Зависимость перемещений характерных точек АТС от времени. Пунктирная линия — для точек А и B вдоль оси y ; сплошные линии — вдоль оси x : черная — для точки А , серая — для точки B

x,y, мм

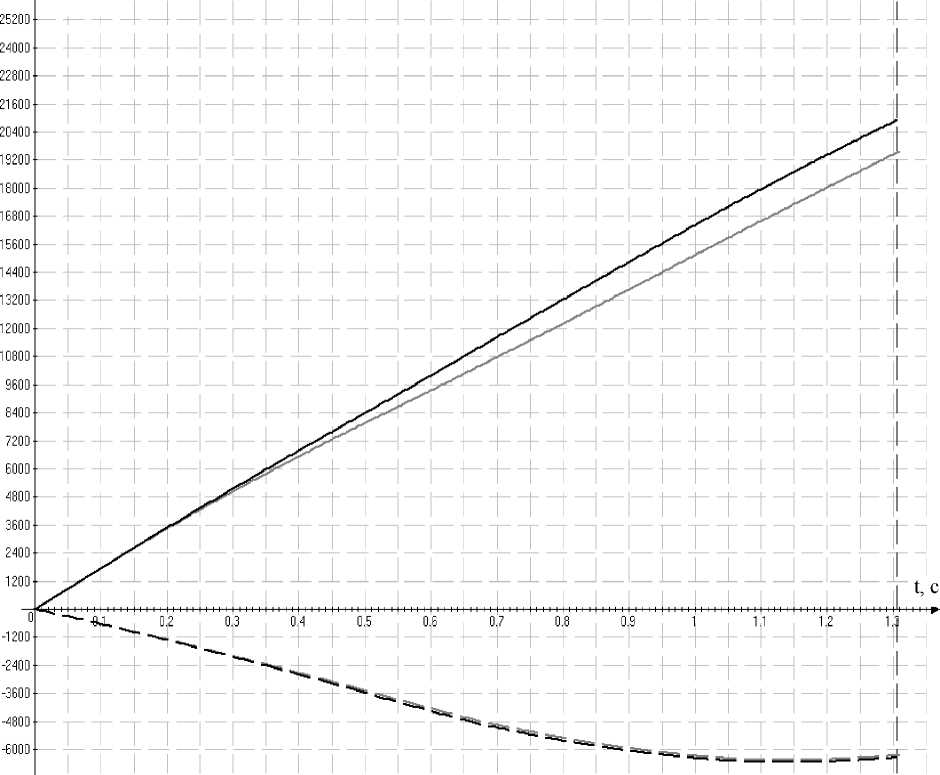
Рис. 9. Зависимость перемещений характерных точек АТС от времени. Пунктирная линия — для точек D и E вдоль оси y ; сплошные линии — вдоль оси x : черная — для точки D , серая — для точки E

Как видно из представленных данных, перемещения точек А , B и D , E вдоль оси y попарно совпадают. Тоже можно наблюдать и для скоростей. Таким образом, при косом наезде АТС на боковые тросовые ограждения движение АТС действительно близко к поступательному.

Обсуждение и заключения. Проведенный анализ кинематических результатов виртуального испытания в сравнении с аналитическими кинематическими расчетами показывает, что представление АТС в качестве материальной точки при его косом наезде на боковые тросовые ограждения является обоснованным, так как движение АТС близко к поступательному. Однако, при необходимости для более точного аналитического расчета кинематических характеристик движения точек, находящихся в областях, близких к точкам C , D , E необходим дополнительный аналитический расчет, например, с использованием уравнений плоскопараллельного движения твердого тела.