Обоснование использования метода конструктивной анизотропии при расчете пологих оболочек двоякой кривизны, ослабленных вырезами
Автор: Каменев И.В., Семенов А.А.
Статья в выпуске: 2, 2016 года.
Бесплатный доступ
Приводится геометрически нелинейная математическая модель деформирования изотропных пологих оболочек двоякой кривизны, ослабленных вырезами. Модель основывается на гипотезах теории оболочек Кирхгофа-Лява и представлена в виде геометрических соотношений, физических соотношений и функционала полной потенциальной энергии. Также приводятся выражения для усилий и моментов. Рассмотрено два способа введения вырезов: дискретно и методом конструктивной анизотропии, который позволяет наиболее точно «размазать» нулевую жесткость вырезов по полю оболочки. Для минимизации функционала применяется метод Ритца, что сводит задачу к решению системы нелинейных алгебраических уравнений, которая решается методом Ньютона. Алгоритм реализован в среде аналитических вычислений Maple 2015. Проводится анализ устойчивости пологих оболочечных конструкций двоякой кривизны, выполненных из стали, при действии на них внешней равномерно распределенной поперечной нагрузки и шарнирно-неподвижном способе закрепления контура оболочки. Расчеты производились при наличии разного числа вырезов, при этом фиксировался коэффициент отношения общей площади вырезов к площади оболочки. Таким образом, при увеличении числа вырезов уменьшался их размер. Распределение вырезов по оболочке делалось двумя разными способами. Для всех исследованных конструкций приводятся значения критических нагрузок потери устойчивости. Проводится сравнение значений, полученных при дискретном введении вырезов и методом конструктивной анизотропии. Для нескольких вариантов конструкций показаны графики «нагрузка - прогиб». Для одного варианта оболочки, ослабленной большим числом вырезов, приводятся поля прогибов до и после потери устойчивости, цветом также показана интенсивность напряжений. На основании полученных данных показано, что при увеличении числа вырезов дискретность их ввода теряется и становится возможным использование специально разработанного метода конструктивной анизотропии. Таким образом, сделано обоснование использования данного метода при расчете устойчивости пологих оболочек, ослабленных большим числом вырезов.
Оболочка, устойчивость, вырезы, ослабленные вырезами оболочки, перфорированные оболочки, математическая модель, метод ритца, метод конструктивной анизотропии, критические нагрузки
Короткий адрес: https://sciup.org/146211614
IDR: 146211614 | УДК: 539.3 | DOI: 10.15593/perm.mech/2016.2.05
Текст научной статьи Обоснование использования метода конструктивной анизотропии при расчете пологих оболочек двоякой кривизны, ослабленных вырезами
PNRPU MECHANICS BULLETIN
Оболочечные конструкции широко применяются в различных областях техники, и их исследование важно для большого числа различных прикладных задач [1–3]. Например, оболочки, ослабленные по технологическим причинам большим числом вырезов (перфорированные оболочки), часто применяются в машиностроении и строительстве [4]. Такие конструкции подвергаются воздействию на них различных нагрузок [5, 6], в связи с этим возникает необходимость исследования их устойчивости. По сравнению с другими видами оболочечных конструкций перфорированным оболочкам посвящено сравнительно мало публикаций [4–16], и их исследование является достаточно актуальной задачей. Обзорных работ в данной области также немного [17–19].
Основная сложность при исследовании оболочек, ослабленных вырезами, состоит в необходимости решения задачи для многосвязной области. Для некоторых простых случаев возможно, применяя аппарат конформных отображений, свести исходную задачу к задаче для односвязной области.
Если рассматривать оболочки, ослабленные вырезами, как оболочки ступенчатопеременной толщины [20], то в дискретно расположенных местах жесткость оболочки принимается нулевой. При этом на границе вырезов, как показано в работе [20], выполняются краевые условия свободного края, которые выполняются тем точнее, чем точнее решается сама краевая задача для таких конструкций. Главное преимущество такого подхода состоит в том, что область интегрирования уравнений равновесия становится односвязной.
Существуют различные математические модели и алгоритмы исследования ослабленных вырезами оболочек. Так, в основе модели могут быть использованы уравнения в смешанной форме [4] или функционал полной потенциальной энергии [13]. В работах [6, 14, 15] исследование проводится на основе метода конечных элементов, а в работах [12, 13] – с применением метода Ритца.
Перфорированные оболочки могут быть выполнены как из изотропных [4, 10, 11, 14], так и ортотропных материалов [6, 11].
В работе [4] рассматриваются статические и динамические задачи для пологих оболочек, перфорированных большим числом вырезов различной формы. Получены аналитические решения на основе сочетания асимптотического подхода и метода гомогенизации.
В работе [15] проводится сравнительный анализ результатов расчета тонких упругих оболочек с вырезами с использованием моментной схемы конечных элементов и программных комплексов «ЛИРА» и SCAD. На примере пологих изотропных панелей показано влияние различных ослаблений на процесс нелинейного деформирования и потерю устойчивости.
В работе [6] методом конечных элементов исследована устойчивость густо перфорированных цилиндрических оболочек под действием внешнего давления. Задача решена на основе теории оболочек с использованием конструктивно ортотропной модели. Получены коэффициенты снижения жесткости при различных значениях пористости. Проведено сравнение численно полученных результатов с аналитическими оценками Э.И. Григолю-ка и Л.А. Фильштинского [8]. Проведено исследование устойчивости упругой цилиндрической перфорированной оболочки под действием внешнего давления для двух вариантов граничных условий. Получены значения критических нагрузок и соответствующие им формы потери устойчивости в зависимости от длины оболочки и степени перфорации.
1. Постановка задачи
Целью данной работы является анализ устойчивости перфорированных пологих оболочек двоякой кривизны и обоснование использования при проведении таких расчетов метода конструктивной анизотропии.
2. Вид рассматриваемых конструкций
Будем рассматривать пологие оболочки прямоугольного плана, ослабленные вырезами, в геометрически нелинейной постановке в рамках теории оболочек Кирхгофа–Лява.
Параметры Ляме и параметры кривизны пологой оболочки соответственно:
A = 1, B = 1, k = 1 , k = 1 .
x R 1 y R 2
Оболочка по контуру закреплена шарнирно-неподвижно, находится под действием равномерно-распределенной поперечной нагрузки q и ослаблена большим числом сквозных вырезов со сторонами, параллельными сторонам оболочки (рис. 1).
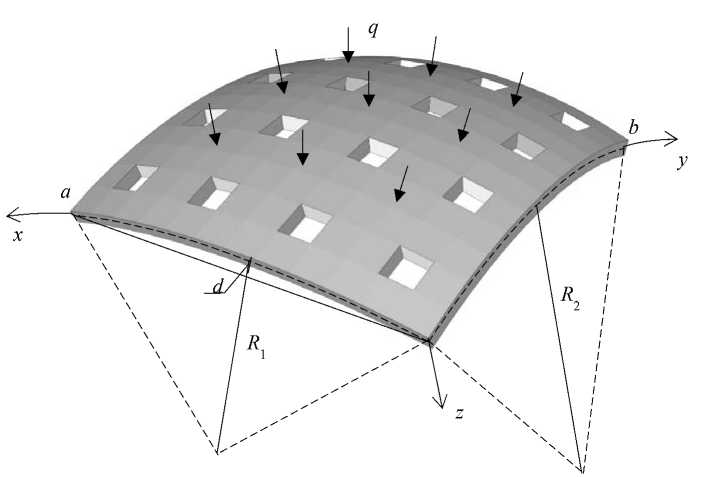
Рис. 1. Схематичное изображение пологой перфорированной оболочки
3. Математическая модель
Математическая модель деформирования пологой оболочки, ослабленной вырезами, состоит из трех групп соотношений:
-
1) геометрических соотношений;
-
2) физических соотношений;
-
3) функционала полной потенциальной энергии.
Геометрические соотношения в срединной поверхности оболочки, связывающие перемещения и деформации, имеют вид д U 1 (д W )
£ =--kW + xx
9 x 2 v d x )
;
ε y
9 V , 1 ( д W Y
--kW + - -- ;
9 y y 2 V 9 y J
д U 9 V 9 W 9 W
Y 11 ,
9 y 9 x 9 x 9 y
где U (x, y ), V (x, y ), W (x, y ) - перемещения точки срединной поверхности оболочки вдоль осей x,y,z соответственно.
В слое, отстоящем на z от срединной поверхности оболочки, деформации принимают вид
£x — £x + 2Х1, £y — £y + 2X2, Yху — Yxy + 2zХ12, где χ1, χ2 – функции изменения кривизн; χ12 – функция изменения кручения, д 2W d2W d2W xi — я 2 ; X2 — я. 2 ; X12 — я я . дx dy дx дy
Физические соотношения – связь напряжений и деформаций – принимают вид
σ
x
E
7-2- ( £x + Н£y ) ; ^y
1 - ц
E
7-7 ( £ y + Ц£ x ) ; Т xy
1 - Ц
γ
2 ( 1 + ц ) xy
Здесь E ,μ – модуль упругости и коэффициент Пуассона материала оболочки.
Места расположения вырезов оболочки можно задать функцией mn
H ( x , у ) = — ZZ h 3 ( x - x y ) S ( y - y i ) , j = 1 i = 1
где h — толщина оболочки; индексы i и j указывают номер (i; j) прямоугольного в плане выреза, стороны которого параллельны осям x и y; n, m - количество вырезов вдоль осей x и у соответственно; 3(x — x-), 3(y — yi) — единичные столбчатые функции, которые представляют собой разности двух единичных функций 3( x — xj ) = U (x — aj ) — — U (x — bj); 3(y — yi) = U (y — ci) — U (y — di). Эти функции равны единице при aj < x < bj, rj ci < y < di, а в остальных точках поверхности оболочки равны нулю. Здесь aj. = x- — —, rj rr
Г у , r i — ширина вырезов в направлении осей x и y со
b = x +—; c = y — -, dt = yt + -; j j 2 i i 2 i i 2
ответственно. Таким образом, толщина оболочки в точке ( x , y ) будет равна h + H ( x , y ) .
Учитывать наличие вырезов будем двумя способами: дискретно и методом конструктивной анизотропии [13]. В зависимости от этого выражения для усилий и моментов будут иметь разный вид.
hh
Интегрируя напряжения по z в пределах от — 2 до ^ + H ( x , y ) , получим вначале усилия и моменты, приходящиеся на единицу длины сечения и приведенные к срединной поверхности оболочки, при дискретном вводе вырезов:
h /2 + H
Nx = J ° xdz =
— h /2
E _ h /2 + H E
7—T( h + F ) ( 8 x + P 8 y ) ; M x = J z ° x dz = -—-2
1 P — h /2 1 P
Г h 3 -A .
12 + J l ( x i +ЦХ 2 ) ;
;
h /2 + H E h /2 + H E Г h 3 ^
N y = J ° ydz = 1— 2 ( h + F ) ( 8 y + p 8 x ) ; My = J z ° ydz = 7^77+ J (X 2 +PX 1 ) ;
— h/2 1 P — h/2 1 P V12 l h/2+H
E
N xy = N yx = J /2 T xy dz = 2^— ) ( h + F ) Y xy ; M xy = M yx
h /2 + H
J z T xy dz =
- h /2
E
h
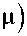
l
X12 ,
где F , J — жесткостные параметры вырезов, n m _ l3 n m _
F = — h ZZ 5 ( x — x -) 3 ( y — y i -) ; J = —77 ZZ 5 ( x — x ) 5 ( y — y ) .
i = 1 j = 1 12 i = 1 j = 1
При использовании метода конструктивной анизотропии усилия и моменты, приходящиеся на единицу длины сечения и приведенные к срединной поверхности оболочки, примут вид [13]
h /2 + H р h /2 + H р
N x = J ° x dz = 73-у( h + F p )(8 x + p 8 y ) ; N y = J ° y dz = 73-y( h + F p )(8 y + p 8 x ) ;
— h/2 1 P — h/2 1 P h/2+H
Mx = J z ° xdz =
— h /2
E
1 —p 2
h 3 T V 1
—+ J p l ( X 1 + PX 2 ) ; M y =
h /2 + H
—J
J z ° ydz = h /2
E
1 — p 2
h
V
—+ J p ( X 2 +PX 1 ) ;
l
N xy = N yx
h /2 + H p
-LT xydz = w( h + F p :; xy ; M y = M yx
h /2 + H
J z T xy dz = - h /2
E
(1 + Ц)
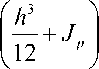
X12 ,
где
h 3
F p =- hAP ; j p =- 12 a p ;
mn
A p 21 r j ■ j = 1 i = 1 ab
Функционал полной потенциальной энергии рассматриваемой оболочки будет иметь вид [21]
ab
E P = J J Nx £ x + N y £ y + 7 ( N xy + N yx ) Y xy + Mx Х 1 + M y X 2 + ( Mxy + Myx ) Х 12 - 2 Q W ] dd • 0 0 L 2
При дискретном введении вырезов более подробно функционал можно записать в виде
+
E p
E ab
2A J J [(h + F)(£ 2 + 2Ц£ x£y + £y + K') +
2 ( 1 Ц ) 0 0
I h3 I/
— + J ( X i + 2цХ 1 Х 2 + X 2 + 2ЦХ 12 )
V 12 7
2 ( 1 - ц2 ) qW
E
dxdy ,
- 1 -ц где р =---- 2
•
А при введении вырезов методом конструктивной анизотропии он запишется следующим образом:
E p
E ab
2\J J [(h + FP )(£ 2 + 2ц£ x£ y + £y + ц7.) +
2 ( 1 ц ) 0 0
I h 3 , X 2 , 2,-22 2О -ц2) qW
+ I ~ + JP (Х 1 + 2ИХ 1 Х 2 + X 2 + 2ИХ 12 )'--- E2----
dxdy •
4. Алгоритм
Для минимизации функционала полной потенциальной энергии применяется метод Ритца, при этом искомые функции U ( x , y ) , V ( x , y ) , W ( x , y ) аппроксимируются в виде
NN N
U ( x , y ) = 2 U ( I ) Z 1( I ); V ( x , y ) = Z V ( I ) Z 2( I ); W ( x , y ) = 2 W ( I ) Z 3( I ), I = 1 I = 1 I = 1
где U ( I ) , V ( I ) , W ( I ) - неизвестные числовые параметры; Z 1( I ) - Z 3( I ) - различные сочетания аппроксимирующих функций X 1 ( I ) - X 3 ( I ) , Y 1 ( I ) - Y 3 ( I ) , удовлетворяющих краевым условиям при шарнирно-неподвижном закреплении контура, в качестве которых можно использовать тригонометрические функции
, X 2 k n x , X ( 2 k - 1 ) n x , x ( 2 k - 1 ) n x
X 1 ( k ) = sin----, X 2 ( k ) = sin-------—, X 3 ( k ) = sin-------—;
aa a
Y 1 ( l ) = sin№, Y 2 ( l ) = sin2 by , Y 3 ( l ) = sin ( 2 1^ .
В соответствии с методом Ритца разложения искомых функций подставляются в функционал (1) или (2), находятся производные по неизвестным числовым параметрам, которые затем приравниваются к нулю. В результате получается система нелинейных алгебраических уравнений, которая решается методом Ньютона.
Также после перехода к безразмерным параметрам [22] для решения полученной системы можно применить метод продолжения решения по наилучшему параметру [23].
В качестве критерия оценки прочности принят критерий Мизеса:
Оi = VO2 -OX°у +^2 + 3т2у ^ О , где от — предел текучести материала; оi — интенсивность напряжений.
Данный алгоритм был реализован в среде аналитических вычислений Maple 2015.
5. Результаты расчетов
Рассматривались три тонкие пологие оболочки, квадратные в плане, входные параметры которых заданы в табл. 1. Рассматриваемые конструкции были ослаблены сквозными вырезами и находились под воздействием равномерно-распределенной поперечной нагрузки q . Оболочки выполнены из стали с модулем упругости E = 210000 МПа и коэффициентом Пуассона ц = 0,3, о т = 428 МПа. Контур конструкции закреплялся шарнирно-неподвижно. Расчеты проводились при удержании N = 16 членов разложения искомых функций в методе Ритца.
Таблица 1
Входные параметры рассматриваемых вариантов оболочек
|
Параметр |
Вариант 1 |
Вариант 2 |
Вариант 3 |
|
Линейный размер а , м |
5,4 |
10,8 |
54 |
|
Главный радиус кривизны R , м |
20,25 |
40,5 |
135,9 |
|
Толщина оболочки h , м |
0,09 |
0,09 |
0,09 |
Распределение вырезов по оболочке проводилось двумя способами. В случае I (рис. 2, а ) оболочка в плане разбивается на участки, число которых равно числу вырезов. Центр участка считается центром соответствующего выреза. Абсцисса i -го выреза вдоль оси x имеет вид a— ( 2 i - 1 ) , а ордината J -го выреза вдоль оси у — 2 m
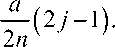
В случае II вырезы распределяются по оболочке равномерно (рис. 2, б ). Абсцисса
, a - r • m ) r центра i -го выреза вдоль оси x имеет вид i I--+ r I — , а ордината J -го выреза ^ m +1 ) 2
. ( a - r • n вдоль оси у равна j I--+ r
I n +1
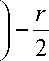
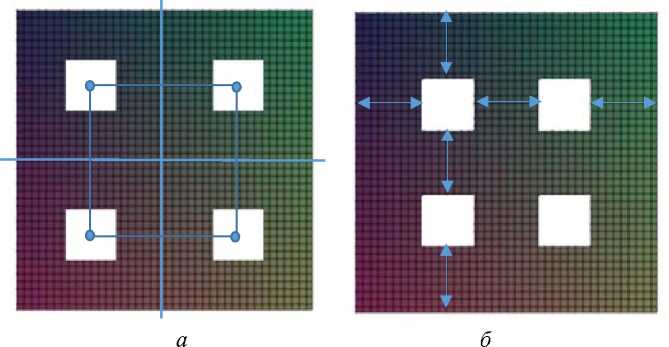
Рис. 2. Схема распределения 4 вырезов по оболочке
Цель исследования – подтвердить сходимость метода конструктивной анизотропии. Предполагается, что сходимость происходит при большом числе вырезов. Покажем это следующим образом. Сначала фиксируется коэффициент относительной площади вырезов Ap , после чего увеличивается число вырезов. Расчеты проводились для числа вырезов > 4, притом рассматриваются только такие наборы вырезов, которые не содержат вырез
в центре конструкции, так как анализ
На всех графиках будем обозначать кривую, полученную с использованием метода конструктивной анизотропии, как Ap , а кривые, полученные путем дискретного ввода вырезов, как I и II для способов распределения вырезов I и II соответственно.
Для оболочки варианта 1 был принят коэффициент A p = 9 . На рис. 2 показаны распределения вырезов по оболочке для способов I и II при 4 вырезах, а на рис. 3 – соответствующие кривые «нагрузка–прогиб». На рис. 4 представлены распределения 24 вырезов по оболочке (слева способ I, справа - II), а на рис. 5 – соответствующие кривые «нагрузка – прогиб».
.
a в точке x = у = —
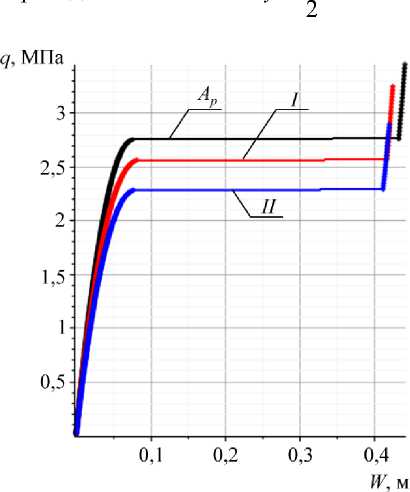
Рис. 3. Кривые «нагрузка–прогиб» для оболочки варианта 1 при 4 вырезах
Результаты расчетов для оболочки варианта 1 при разном числе вырезов сведены в
табл. 2. В первом столбце находится общее число вырезов M = 2
m • n
, где квадратные
скобки обозначают целочисленное деление; во втором – относительный размер выреза r ; в третьем – критическая нагрузка потери устойчивости qkArp , полученная методом a r

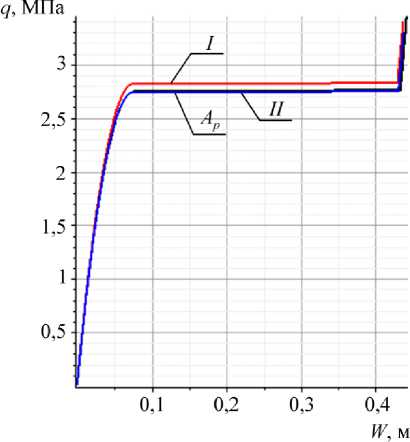
Рис. 5. Кривые «нагрузка–прогиб» для оболочки варианта 1 при 24 вырезах
конструктивной анизотропии; в четвертом и пятом – критические нагрузки потери устойчивости qkIr и qkIrI , полученные путем дискретного ввода вырезов по способам их распределения I и II соответственно; в шестом и седьмом – Aqkr = -qp и AqP/= qp. Если Aqi qkr qkr и Aql попадают в интервал [0,95; 1,05], то считаем, что метод конструктивной анизотропии сходится к дискретному вводу вырезов.
На рис. 6 показан график зависимости относительной критической нагрузки потери устойчивости A q kr от общего числа вырезов M для способов распределения вырезов I и II.
Таблица 2
Результаты для оболочки варианта 1 при Ap = 9
|
M |
r a |
Критические нагрузки потери устойчивости |
A q kr |
A q |
||
|
q kArp , МПа |
q kIr , МПа |
q kIrI , МПа |
||||
|
4 |
0,1667 |
2,7599 |
2,5699 |
2,2899 |
0,9312 |
0,8297 |
|
6 |
0,1361 |
2,5799 |
2,3899 |
0,9348 |
0,8659 |
|
|
8 |
0,1179 |
2,8799 |
2,6499 |
1,0435 |
0,9601 |
|
|
12 |
0,0960 |
2,6200 |
2,5400 |
0,9493 |
0,9203 |
|
|
16 |
0,0833 |
2,6399 |
2,6299 |
0,9565 |
0,9529 |
|
|
20 |
0,0745 |
2,7299 |
2,6700 |
0,9891 |
0,9674 |
|
|
24 |
0,0680 |
2,8299 |
2,7499 |
1,0254 |
0,9964 |
|
|
36 |
0,0555 |
2,7599 |
2,7100 |
1,000 |
0,9819 |
|
|
48 |
0,0481 |
2,7899 |
2,7399 |
1,0109 |
0,9927 |
|
64 0,0417 2,7859 2,7478 1,0094 0,9956
На основании рис. 6 и данных в табл. 2 можно сделать вывод, что метод конструктивной анизотропии для оболочки варианта 1 сходится при числе вырезов M > 16.
В табл. 3 показаны аналогичные данные для оболочки варианта 2, а на рис. 7 – график зависимости относительной критической нагрузки от общего числа вырезов для способов распределения вырезов I и II.
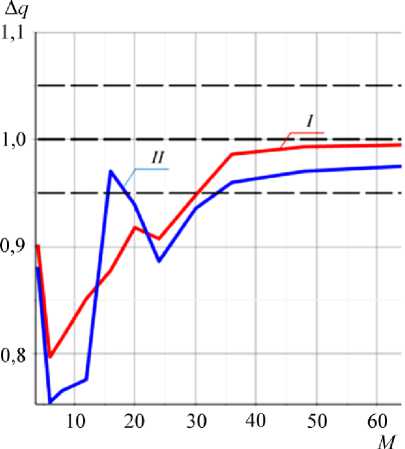
Рис. 7. График зависимости относительной критической нагрузки потери устойчивости от числа вырезов для оболочки варианта 2
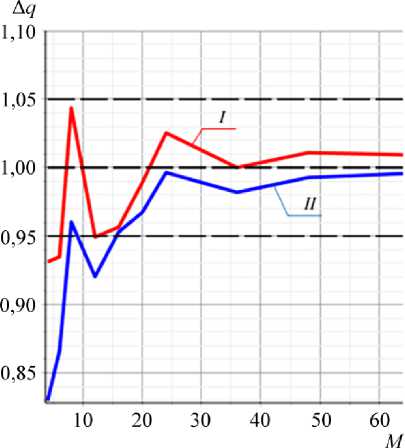
Рис. 6. График зависимости относительной критической нагрузки потери устойчивости от числа вырезов для оболочки варианта 1 1 при A p = 9
при A = — p 25
Таблица 3
Результаты для оболочки варианта 2 при A p =
|
M |
r a |
Критические нагрузки потери устойчивости |
А q k |
^ q I |
||
|
q kArp , МПа |
q kIr , МПа |
q kIrI , МПа |
||||
|
4 |
0,2000 |
0,7138 |
0,6438 |
0,6288 |
0,9019 |
0,8809 |
|
6 |
0,1633 |
0,5688 |
0,5388 |
0,7968 |
0,7548 |
|
|
8 |
0,1414 |
0,5813 |
0,5463 |
0,8144 |
0,7653 |
|
|
12 |
0,1155 |
0,6075 |
0,5538 |
0,8511 |
0,7758 |
|
|
16 |
0,1000 |
0,6263 |
0,6925 |
0,8774 |
0,9702 |
|
|
20 |
0,0894 |
0,6550 |
0,6700 |
0,9177 |
0,9387 |
|
|
24 |
0,0816 |
0,6475 |
0,6325 |
0,9072 |
0,8862 |
|
|
30 |
0,0730 |
0,6763 |
0,6675 |
0,9475 |
0,9352 |
|
|
36 |
0,0667 |
0,7038 |
0,6850 |
0,9860 |
0,9597 |
|
|
48 |
0,0577 |
0,7088 |
0,6925 |
0,9930 |
0,9702 |
|
|
64 |
0,0500 |
0,7100 |
0,6957 |
0,9947 |
0,9748 |
|
Как видно из графика (см. рис. 7) и табл. 3, метод конструктивной анизотропии для оболочки варианта 2 сходится при M > 36.
Пользуясь полученными данными, предположим, что для оболочки варианта 3 метод
конструктивной анизотропии сойдется уже при M = 36.
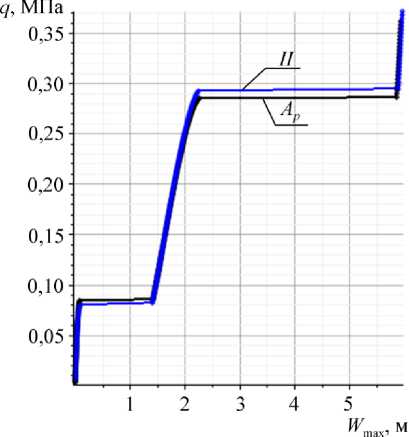
На рис. 8 показан график «нагрузка -наибольший прогиб» для оболочки варианта 3 при способе задания вырезов II. При этом A q kl = 0,9728, то есть метод конструктивной анизотропии здесь также сходится.
Также интерес могут представлять поля прогибов и напряжений рассматриваемых конструкций. На рис. 9, 10 показаны состояния конструкции для оболочки варианта 3 при M = 36 до и после местной потери устойчивости. Цветом показана интенсивность напряжений ст i . Часто при отображении оболочки с наложенным по-
Рис. 8. Кривая «нагрузка – наибольший прогиб»
лем прогибов, особенно до потери устой-для варианта оболочки 3 при способе введения чивости, значения прогибов настолько ма-вырезов II лы, что их достаточно трудно заметить.
Тем не менее даже малозаметные изменения в конструкции могут нести в себе важную информацию о ее состоянии. В связи с этим значения прогиба умножаются на масштабирующий коэффициент k m = 2.
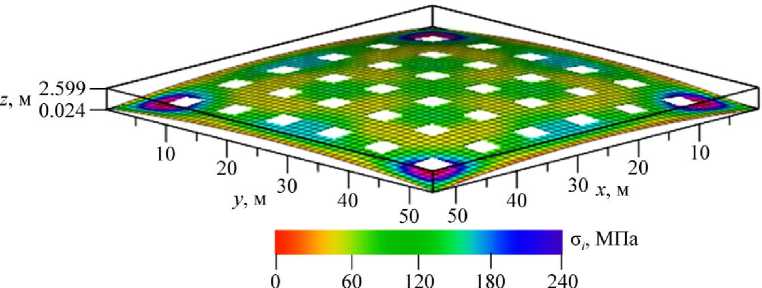
Рис. 9. Вариант оболочки 3 до потери устойчивости
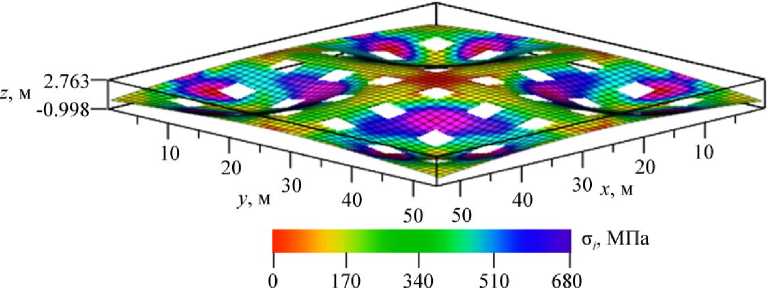
Рис. 10. Вариант оболочки 3 после потери устойчивости
Из данных на рис. 10 видно, что интенсивность напряжений превышает значения предела текучести с т = 428 МПа. Таким образом, потеря прочности происходит во время местной потери устойчивости.
Заключение
В ходе исследования были рассмотрены две математические модели деформирования пологих оболочек, ослабленных вырезами. В первой модели вырезы вводятся дискретно с помощью единичных столбчатых функций, задающих места расположения вырезов. Во второй модели используется метод конструктивной анизотропии, позволяющий «размазать» нулевую жесткость вырезов по полю оболочки.
Использование математической модели оболочки ступенчато-переменной толщины, когда область интегрирования является односвязной, не вызывает в дальнейшем существенных трудностей при проведении расчетов.
Были исследованы три варианта оболочек при разном числе вырезов. В результате было продемонстрировано, что при увеличении числа вырезов дискретность их ввода теряется и становится возможным использование метода конструктивной анизотропии. При способе задания вырезов I потеря устойчивости наступает позднее, чем при способе задания вырезов II.
Критерием использования метода конструктивной анизотропии для оболочек, ослабленных вырезами, являются два фактора: отношение общей площади вырезов к площади оболочки ( Ap ) и отношение ширины выреза к линейному размеру оболочки ( r / a ). При A p = 0,111 решение, полученное по методу конструктивной анизотропии, практически совпадает с решением, полученных при дискретном введении вырезов при r / a < 0,083 . При A p = 0,16 должно выполняться условие r / a < 0,067. Таким образом, чем меньше Ap , тем больше может быть r / a , но не превосходить 0,09.
Работа выполнена при поддержке Минобрнауки РФ, проект № 3801.
Список литературы Обоснование использования метода конструктивной анизотропии при расчете пологих оболочек двоякой кривизны, ослабленных вырезами
- Elastic Buckling Analysis of Ring and Stringer-stiffened Cylindrical Shells under General Pressure and Axial Compression via the Ritz Method/G. Arani, A. Loghman, A.A. Mosallaie Barzoki, R. Kolahchi//Journal of Solid Mechanics. -2010. -Vol. 2. -No. 4. -P. 332-347.
- Vibration analysis of ring-stiffened conical-cylindrical-spherical shells based on a modified variational approach/Y. Qu, S. Wu, Y. Chen, H. Hua//International Journal of Mechanical Sciences. -2013. -Vol. 69. -P. 72-84 DOI: 10.1016/j.ijmecsci.2013.01.026
- A semi-analytical model for local post-buckling analysis of stringer-and frame-stiffened cylindrical panels/P. Buermann, R. Rolfes, J. Tessmer, M. Schagerl//Thin-Walled Structures. 2006. -Vol. 44. -P. 102-114 DOI: 10.1016/j.tws.2005.08.010
- Kalamkarov A.L., Andrianov I.V., Weichert D. Asymptotic analysis of perforated shallow shells//International Journal of Engineering Science. -2012. -Vol. 53. -P. 1-18 DOI: 10.1016/j.ijengsci.2011.12.005
- Buckling Optimization of Perforated Curved Shells/Wang D. //Materials Science Forum. -2012. -Vol. 697-698. -P. 614-617 DOI: 10.4028/www.scientific.net/MSF.697-698.614
- Numerical modeling of perforated shells stability/А.А. Antipov, A.A. Artemyeva, V.G. Bazhenov, M.N. Zhestkov, A.I. Kibec//PNRPU Mechanics Bulletin. -2015. -No. 1. -Р. 21-30 DOI: 10.15593/perm.mech/2015.1.02
- Ghergu M., Griso G., Miara B. Homogenization of thin piezoelectric perforated shells//Mathematical Modeling and Numerical Analysis. -2007. -Vol. 41. -P. 875-895 DOI: 10.1051/m2an:2007046
- Григолюк Э.И., Фильштинский Л.А. Перфорированные пластины и оболочки. -М.: Наука, 1970. -556 с.
- Fazilati J., Ovesy H.R. Finite strip dynamic instability analysis of perforated cylindrical shell panels//Composite Structures. -2012. -Vol. 94. -P. 1259-1264 DOI: 10.1016/j.compstruct.2011.11.008
- Guz A.N., Storozhuk E.A., Chernyshenko I.S. Elastoplastic state of flexible cylindrical shells with two circular holes//International Applied Mechanics. -2004. -Vol. 40. -No. 10. -P. 1152-1156 DOI: 10.1007/s10778-005-0022-7
- Maksimyuk V.A., Storozhuk E.A., Chernyshenko I.S. Nonlinear Deformation of Thin Isotropic and Orthotropic Shells of Revolution with Reinforced Holes and Rigid Inclusions//International Applied Mechanics. -2013. -Vol. 49. -No. 6. -P. 685-692 DOI: 10.1007/s10778-013-0602-x
- Преображенский И.Н. Устойчивость и колебания пластинок и оболочек с отверстиями. -М.: Машиностроение, 1981. -191 с.
- Карпов В.В., Игнатьев О.В., Сальников А.Ю. Нелинейные математические модели деформирования оболочек переменной толщины и алгоритмы их исследования. -М.: АСВ; СПб.: Изд-во С.-Петерб. гос. архит.-строит. ун-та, 2002. -420 с.
- Баженов В.А., Кривенко О.П., Соловей Н.А. Нелинейное деформирование и устойчивость упругих оболочек неоднородной структуры. -М.: ЛИБРОКОМ, 2012. -329 с.
- Соловей Н.А., Кривенко О.П., Малыгина О.А. Конечноэлементные модели исследования нелинейного деформирования оболочек ступенчато-переменной толщины с отверстиями, каналами и выемками//Инженерно-строительный журнал. -2015. -№ 1(53). -С. 56-69 DOI: 10.5862/MCE.53.6
- Eccher G., Rasmussen K.J.R., Zandonini R. Geometric nonlinear isoparametric spline finite strip analysis of perforated Thin-Walled Structures//Thin-Walled Structures. -2009. -Vol. 47. -P. 219-232 DOI: 10.1016/j.tws.2008.05.013
- Guz' A.N., Ashmarin Yu.A. Stability of a shell, weakened by holes (review)//Soviet Applied Mechanics. -1973. -Vol. 9. -Iss. 4. -P. 349-358 DOI: 10.1007/BF00882643
- Preobrazhenskii I.N. Stability of thin-walled shells with holes (survey). Part 1//Strength of Materials. -1982. -Vol. 14. -Iss. 1. -P. 23-35 DOI: 10.1007/BF00769180
- Preobrazhenskii I.N. Stability of thin shells with cutouts (review). Part 2//Strength of Materials. -1982. -Vol. 14. -Iss. 2. -P. 218-225 DOI: 10.1007/BF00769060
- Ильин В.П., Карпов В.В. Устойчивость ребристых оболочек при больших перемещениях. -Л.: Стройиздат. Ленигр. отд-ние, 1986. -168 с.
- Карпов В.В. Прочность и устойчивость подкрепленных оболочек вращения: в 2 ч. Ч.1: Модели и алгоритмы исследования прочности и устойчивости подкрепленных оболочек вращения. -М.: Физматлит, 2010. -288 с.
- Карпов В.В., Семенов А.А. Безразмерные параметры в теории подкрепленных оболочек//Вестник Пермского национального исследовательского политехнического университета. Механика. -2015. -№ 3. -С. 74-94 DOI: 10.15593/perm.mech/2015.3.07
- Kuznetsov E.B. Continuation of solutions in multiparameter approximation of curves and surfaces//Computational Mathematics and Mathematical Physics. -2012. -Vol. 52. -No. 8. -P. 1149-1162 DOI: 10.1134/S0965542512080076


