Обоснование методики расчета запасных частей для устранения параметрических отказов гидропривода лесных машин

При определении количества замен (запасных частей) для устранения параметрического отказа гидропривода ЛЗМ основной характеристикой процесса восстановления является функция восстановления [1], которая численно равна математическому ожиданию количества замен N Д при наработке T :

to

N Д — Z F ( T ) •              (1)

i = 1

где F i ( T ) - функция распределения ресурсов заменяемых деталей ( i -х замен).

Чтобы выявить фактическое распределение ресурсов заменяемых деталей, требуются длительные эксплуатационные испытания, что затрудняет определение объема технических воздействий и расхода запасных частей. Одним из способов преодоления этих трудностей является метод расчета запасных частей на использовании скорости или интенсивности изнашивания деталей [2], так как получить такие данные можно при сравнительно небольшой наработке, не ожидая отказа детали (сопряжения).

Принимая процесс изнашивания близким к линейному [3], исходное уравнение для определения наработки детали до отказа приближенно можно записать в следующем виде:

_т _ ^A n — ^A 0

T n — _

где Т ₀ - наработка детали до отказа, моточас.; A _n - предельно допустимое значение износа, мкм; А ₀ - начальное значение износа, мкм; к -интенсивность изнашивания, мкм/1000 моточас.

Наработка детали до отказа зависит от многих случайных факторов, поэтому ее можно рассматривать как случайную величину, вид распределения которой может быть различным. Воспользуемся известным в математике приемом, согласно которому любую непрерывную можно с любой степенью точности заменить многочленом n-й степени, то есть плотность интенсивности изнашивания можно записать в виде:

f ( к ) — a ₀ + а 1 • к + а ₂ • к ² + ... + a n • k ⁿ , (3) где а ₀, а _р..., a n - коэффициенты многочлена.

Зависимость (1) можно рассматривать как функцию случайного аргумента a . Плотность распределения ресурса можно выразить известной формулой:

f (T) = toфТT)ф‘(T)|] , (4)

где ф ( T ) - обратная функция ф ( T ) ; | ф '( T ) -абсолютное значение производной от обратной

функции.

С учетом выражений (2) и (3) и рекомендаций работы [2] плотность распределения ресур- са можно представить в следующем виде:

^ ( ^T ) =

to                             /to

J T2 f (T) dT - J Tf (T) dT

-to                        l -to

. (11)

Подставив в формулу (11) значение функции для усеченного распределения и решив интегралы с учетом принятых обозначений (8) и (9), согласно работе [3], получим зависимость:

^ ( ^T ) = ^A R ^- A ° J R c ( k ) • ^R 2 ( k ) - R ( k ) , (12)

n

f (T )=X i=0

a n ( A n —A o ) n ⁺ 1

m n + 2

где

R ₂ ( k ) = a ₀

l ^k 1

1 |        , ^k 2            ^an ( , n - 1

— | + ajln— + У   -(k2 - k2 J        ki    2 n -1

По найденной плотности распределения, как известно, можно определить средний ресурс исследуемого сопряжения (детали):

Расход запасных частей, используя выражения T_cp и c r( T ) , можно определить по известной в теории надежности формуле:

to

T p = J T • f ( T ) dT .             (6)

T

M (T ) = T- + ^

T ср

(t( t ) Vt ср

Согласно рекомендациям работ [1], [2], задавая минимальное K ₁ и максимальное K ₂ значения интенсивности изнашивания:

_T ^A n ^{- A}o „ _T^A n ^{- A} 0

T = и T = , 1         k ₂            2 k ₁

средний ресурс детали с учетом его усеченного распределения может быть определен по формуле:

где M ( T ) - расход запчастей, шт.; T - наработка объекта с начала эксплуатации, моточас.; ^_а – квантиль нормального распределения в зависимости от принятой доверительной вероятности P = 1 - а ; а - риск недостаточности числа запасных частей.

Подставляя в формулу (13) зависимости (10) и (12), получим:

T ср

^(A n ^{- A} 0 )

a o • In k - X a ( k 2 - k n )

k _{1     1} n

n

У      k n ^{+ 1} -

Xn +1( 2

. (7)

M (T ) =

R c ( k ) T

R1 (k )(A n-A0)

1 ₊ ^ V ^A n ^-A 0 ^R 2 ( ^k ) ^R 1 ( ^k J

VT     VR1 (k) Rc (k)

Для упрощения записи введем обозначения:

R i ( k ) = a o ln k ■ X ^a ( k 2n - k n ) , k 1 1 n

n

Rc ( k ) = X -n? •(k2+1 — kn+1).

0 n + 1

Неизвестные коэффициенты многочлена (3): a ₀ , a ₁ , ..., a_n , согласно рекомендациям работы [4], можно найти по экспериментальным данным интенсивностей изнашивания деталей, используя метод наименьших квадратов, а именно метод Чебышева. Выражение для определения искомых коэффициентов имеет вид:

С учетом принятых обозначений формула (7) будет иметь вид:

f (k )=

XW

M

+X w • V1 (ki)+ X V2 (ki)

= R1(k)(A, "A,)

"     Rc ( ^k )      '

+ ... +

XWi • Vn (ki) X V (k)

Vn ( k ) ,

Среднее квадратическое отклонение c r( T ) среднего ресурса при этом равно:

где X Wi - сумма частот статистического ряда интенсивностей изнашивания; M – число ин- тервалов статистического ряда; Vn (к,) - коэффициенты полиномов Чебышева.

Согласно работе [4], зависимости V n ( к ) определяются для каждого члена ряда (15) по следующим формулам:

V ( к ) = к - M ;'' Б,             (16)

Рассмотрим применение метода Чебышева на условном числовом примере. При исследовании интенсивности изнашивания деталей ше-

стеренного насоса получен статистический ряд, представленный в табл. 1.

Найдем для этого ряда многочлен n-й степени. Для этого вычислим сначала первый член ряда (15), то есть уравнение нулевого порядка:

f , ( к ) =

W

= _ = 0,091.

M 11

V3 (к) = | к -

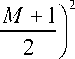
3 M ² + 7 Л M + 1 А ------- к--

20 (      2 )

, (18)

Найдем сумму квадратов разностей для этого уравнения:

V 4 ( к ) = f к - M 2- А -

- -1(3 M 2 - 13) ^f к - M il 1 2 + A M Ml M M. ^<19)

14           i(       2 )           560

Ошибка ( s n ) приближенного многочлена выражается формулой:

_ _ ,  (У W )         I²

У = у W ² -= 0,1352 - !_ = 0,0442.

0 i M 11

Вычисляем ошибку приближения:

0,0442

А 11 - 1

= 0,065.

£

Е

M-(n +1)

где Е n — сумма квадратов разностей между экспериментальными данными и определяемым многочленом.

Затем определим второй член ряда по формуле (15). Для этого, согласно формулам (16–19), делаем соответствующие вычисления или берем значения коэффициентов из таблицы [5], соответствующей числу интервалов ряда M = 11.

Составим табл. 2, где значения V , ( к , ) приведены в четвертой колонке, а сумма квадратов – внизу этой колонки. Вычислим произведения WV ( к , ) и занесем эти данные в пятую колонку табл. 2. Определим сумму этих произведений и запишем внизу пятой колонки.

Таблица 1

	Исходные данные				условного		примера
Значение k в интервале	0...1	1...2	2...3	3...4	4...5	5...6	6...7	7...8	8...9	9...10	10...11	сумма
Частность W	0,05	0,08	0,16	0,2	0,18	0,12	0,10	0,05	0,03	0,02	0,01	1,0
W 2	0,0025	0,0064	0,0256	0,04	0,0324	0,0144	0,01	0,0025	0,0009	0,0004	0,0001	0,132

Таблица 2

		Результаты		промежут	очных рас	четов
k	W	W 2	V ( к )	WV ( к , )	V 2 ( к , )	WV 2 ( к , )	V 3 ( к , )	WV 3 ( к , )
1	2	3	4	5	6	7	8	9
0–1	0,05	0,0025	-5	-0,25	+15	+0,75	-30	-1,5
1–2	0,08	0,0064	-4	-0,32	+6	+0,48	+6	+0,48
2–3	0,16	0,0256	-3	-0,48	-1	-0,16	+22	+3,52
3–4	0,20	0,040	-2	-0,40	-6	-1,20	+23	+4,6
4– 5	0,18	0,0324	-1	-0,18	-9	-1,62	+14	+2,52
1	2	3	4	5	6	7	8	9
5–6	0,12	0,0144	0	0	-10	-1,2	0	0
6–7	0,10	0,01	+1	+0,10	-9	-0,90	-14	-1,40
7–8	0,05	0,0025	+2	+0,10	-6	-0,30	-23	-1,15
8–9	0,03	0,0009	+3	+0,09	-1	-0,03	-22	-0,66
9–10	0,02	0,0004	+4	+0,08	+6	+0,12	-6	-0,12
10–11	0,01	0,0001	+5	+0,05	+15	+0,15	+30	+0,30
Сумма Е	1,0	0,1352	V 1 2 ( K , ) 110	-1,21	V 2 2 ( К ) 856		[ V 3 ( К ) ] 2 4299	+6,59

Подставив полученные данные, найдем второй член ряда (15):

EWV(Mf, M+1)

E V 2 ( kW "  2 J"

- 1,21 ^f k - ^{11 + 1} ) = 0,066 - 0,011 k .

110 V 2 J

Сложив найденный результат с правой частью уравнения нулевого порядка, найдем уравнение первого порядка:

/ 1 ( k ) = 0,091 + 0,066 - 0,011 k = 0,157 + 0,011 k .

Вычислим разность квадратов и определим ошибку приближения:

[ E wv ( ^k i ) ] ² E V 2 (M

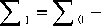
= 0,0442--,--- = 0,0318.

⁸ 1 =

0,0318

11 - 2

= 0,059.

Аналогично найдем третий член ряда (15) и уравнение второго порядка:

f , ( k ) = 0,039 + 0,0437 k - 0,00456 k ².

Ошибка приближения при этом составит 8 2 = 0,0418, то есть она снизилась по сравнению с 8 1 . Следовательно, необходимо повышать дальше порядок многочлена, пока ошибка приближения не перестанет заметно уменьшаться.

Вычисляем четвертый член ряда (15) и находим уравнение третьего порядка:

/ ₃ ( k ) = - 0,107 + 0,159 k - 0,0276 k ² + 0,0012 k ³.

Ошибка приближения для этого уравнения составляет 8 3 = 0,0236. Ошибка приближения, как показывает практика расчетов [5], при дальнейших расчетах уменьшается мало. Вычислить многочлен выше четвертого и даже третьего порядка нет надобности.

Оценка погрешностей представленных зависимостей для определения ресурса деталей и числа запчастей применительно к конкретным сопряжениям конкретных узлов гидропривода ЛЗМ может быть осуществлена сопоставлением фактических и расчетных данных об износе и о расходе запасных частей в условиях рядовой эксплуатации в зависимости от фактической наработки исследуемых объектов.

Для ускорения расчетов запасных частей по изложенной методике может быть построена номограмма, состоящая из двух частей: левой и правой.

Один из вариантов возможной (условной) номограммы представлен на рисунке. На горизонтальных шкалах левой части номограммы отложены значения А , на нижней от 0 до 650 мкм, а на верхней от 0 до 9700 мкм. Начало отсчета у них различное: у нижней – возрастание значений идет слева направо, у верхней – наоборот. Такое расположение этих шкал вызвано различным их применением. Верхняя шкала предназначена для деталей, имеющих большие отклонения предельно допустимых размеров А и больше интенсивности изнашивания (поршневые и штоковые уплотнения и другие быстроизнашиваемые металлические детали), а нижняя – для деталей с небольшими отклонениями размеров и интенсивностями изнашивания. Для удобства записи значения А на верхней шкале уменьшены в 100 раз, а на нижней – в 10 раз.

На вертикальной шкале левой части номограммы отложены значения

А

R , ( k ) R ( k ) ^,

то есть средний ресурс детали.

Такое построение номограммы вызвано тем, что при подстановке в формулу (6) значения функции (5) получим интервал, который расходится при T = 0 и T = да , а на остальном промежутке сходится. Это хорошо согласуется с физической сущностью рассматриваемой модели процесса изнашивания, согласно которой принятое допущение о постепенном изменении размеров детали означает, что она не может отказать мгновенно, и наоборот – не может работать бесконечно долго без износа. В связи с этим, как уже говорилось, в данном случае необходимо рассматривать усеченное распределение . При этом коэффициент усечения ( S ) можно найти из условия [4]:

T 2

S J f (T) dT = 1.

T 1

Для нахождения величины среднего ресурса надо опустить перпендикуляр из точки, соответствующей значению износа А для данной детали, до пересечения с линией, на которой указаны пределы варьирования интенсивности изнашивания ( K i ) , а затем из этой точки провести горизонтальную линию до пересечения с вертикальной шкалой. При этом следует учитывать, что для нижней шкалы пучок веерных линий с обозначенными интенсивностями изнашивания выходит из левого нижнего угла, а для верхней шкалы – из правого.

Правая часть номограммы предназначена для определения потребности в запчастях в зависимости от среднего ресурса детали (определяется в левой части номограммы или задается), нара- ботки объекта с начала эксплуатации T и доверительной вероятности P . На нижней горизонтальной шкале правой части номограммы отложены значения

T • Rc (k)

AR1 (k) , то есть математическое ожидание расхода запасных частей, на вертикальной – потребность в запасных частях на ресурсную наработку объекта (наработку до предельного состояния).

Порядок определения потребности в запасных частях с помощью номограммы рассмотрим на примере. Находим точку пересечения перпендикуляра, восстановленного, например, из A = 430 мкм нижней шкалы левой части номограммы, с линией, соответствующей пределам варьирования интенсивности изнашивания данной детали. Из этой точки проводим горизонтальную прямую до пересечения с кривой правой части номограммы, на которой указана соответствующая наработка на отказ, и из этой точки проводим вертикальную прямую до пересечения с линией с заданной горизонтальной вероятностью. Полученную точку пересечения проектируем на вертикальную шкалу правой части номограммы, на которой указана искомая потребность в запасных частях. Порядок поиска решения на номограмме указан штриховыми линиями со стрелками.

Когда нет данных по интенсивности изнашивания и предельно допустимому отклонению размеров детали, но известен средний ее ресурс, потребность в запасных частях по номограмме определяется так. Из точки, соответствующей среднему ресурсу детали, на вертикальной шкале левой части номограммы проводим горизонтальную прямую до пересечения с линией, на которой указан средний ресурс до предельного состояния, в правой части номограммы. Затем из этой точки проводим вертикальную прямую до пересечения с линией, соответствующей заданной доверительной вероятности, проектируем эту точку на вертикальную шкалу правой части номограммы и находим потребность в запасных частях.

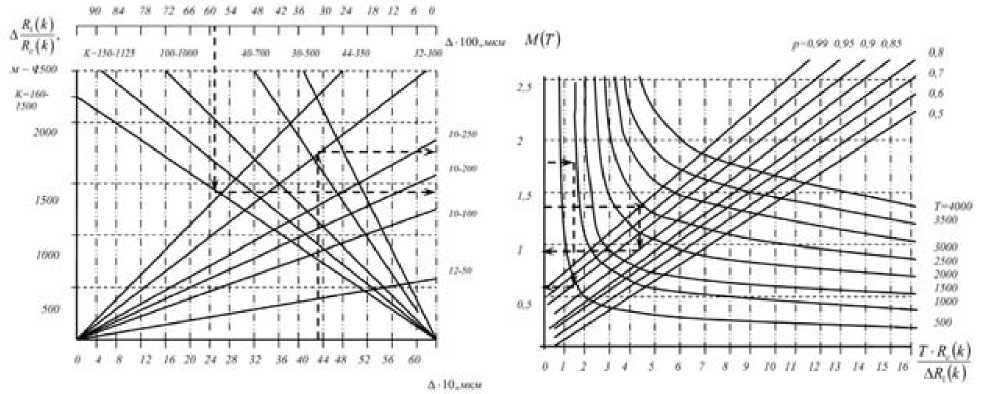
Номограмма для определения объема технических воздействий (замен деталей) при постепенных (параметрических) отказа