Обоснование параметров резервных орбит при выведении космического аппарата в случае возникновения нештатных условий

Обстоятельства, возникающие при запусках космических аппаратов и непредусмотренные штатными условиями выведения, ведут к появлению нештатных условий подготовки и пуска, а также полёта средств выведения (СВ) на активном участке траектории. Следствиями нештатных условий полёта СВ являются аварии, ча-

стично успешные пуски, а также выведение КА на штатные орбиты с замечаниями в технических отчётах по результатам пусков. Нештатные условия подготовки и пуска СВ могут приводить к переносу запусков КА, авариям на старте и к нештатным условиям полёта СВ [1]. В результате частично успешных пусков СВ космические аппараты оказываются на нерасчётных орбитах, где они решают целевые задачи с заниженными показателями качества или считаются «утерянными» из-за невозможности решения этих задач. Выведение КА на такие орбиты происходит из-за того, что, закладываемая в настоящее время в системы управления движением (СУД) СВ, концепция предполагает выведение КА на орбиты, параметры которых максимально приближены к параметрам штатных целевых орбит. Реализованный подход является обоснованным, если целевые орбиты при сложившихся нештатных условиях полёта находятся в областях достижимости СВ. В противном случае – пуски СВ оказываются частично успешными, хотя в областях достижимости имелось значительное количество орбит КА, среди которых могли быть приемлемые, с точки зрения результативности решения целевых задач (связи, метеорологического обеспечения, навигации и т. д.). Эта ситуация является отправной точкой для разработки новой концепции, требующей внесения изменений в перечень задач управления движением, решаемых до пуска СВ и в процессе полёта на борту, а также обоснования параметров орбит КА, названных резервными [1].

Из всего многообразия возможных орбит КА в результате практического решения задач освоения космического пространства можно выделить (классифицировать) лишь немногие (целевые, опорные, промежуточные и т. д.). Среди них понятия «резервные» до некоторого времени не существовало [1, 2].

Резервными орбитами будем называть целевые орбиты конкретного КА или однотипных КА, лежащие в областях достижимости СВ, на которые может выводиться КА в случаях возникновения нештатных условий полёта СВ и обеспечивающие при этом наибольшую результативность решения целевых задач.

Решение задачи перенацеливания СВ на резервную орбиту представляет определенные трудности с математической и вычислительной точек зрения. Ограниченные ресурсы бортовой цифровой вычислительной машины (БЦВМ) и необходимость решения одновременно целого комплекса задач, выдвигают жесткие требования к методам и алгоритмам синтеза траектории выведения КА. Анализ результатов, полученных другими авторами [3-5], позволяет сделать вывод, что ограниченные возможности БЦВМ, сложность алгоритмов и проблемы сходимости решения предполагают применение метода декомпозиции задачи наведения СВ на новую орбиту на две части – наземную (решаемую до старта СВ) и бортовую (решаемую в реальном масштабе времени).

При решении наземной части задачи синтеза обосновываются параметры резервных орбит КА, выявляется перечень нештатных ситуаций, время их возникновения, оцениваются возможности СУД по осуществлению управляемого полёта, строится область достижимости и формируется структура программы управления движением.

После решения наземной части задачи синтеза в запоминающее устройство бортового комплекса управления движением СВ на основе проведённых до старта исследований закладывается перечень нештатных ситуаций и значения параметров, позволяющие их идентифицировать и синтезировать новую траекторию движения, программы движения, энергетическая характеристика СВ, построенная в зависимости от времени возникновения соответствующей нештатной ситуации, а также параметры резервных орбит. При этом поиск параметров программы полёта сводится к последовательности решения краевых задач.

Зная энергетические возможности СВ по доставке КА на орбиту максимальной высоты из сложившейся нештатной ситуации, можно выбрать резервную орбиту, обоснованную и заложенную до старта в БЦВМ СУД.

Большинство задач, решаемых с помощью КА, может быть сведено к сбору или передаче информации с поверхности Земли. В этом случае говорят о системах КА обзора поверхности Земли [1,6-11]. Рассмотрим вопрос обоснования параметров резервных орбит для систем сбора и передачи информации с поверхности Земли на круговых орбитах, как систем обеспечивающих обзор поверхности Земли с разрывом в наблюдении – систем КА периодического обзора поверхности Земли.

ПОСТАНОВКА ЗАДАЧИ

Среди множества достижимых орбит, на которые может быть выведен КА системы периодического обзора поверхности Земли, выбрать такие, на которые может выводиться КА в случаях возникновения нештатных условиях полёта СВ, и обеспечивающие при этом наибольшую результативность решения целевых задач. Рассмотрим только круговые орбиты.

Исходными данными для расчёта параметров резервных орбит являются:

• а)    параметры штатной орбиты, на которую должен быть выведен КА ( i – наклонение орбиты, H – высота орбиты, Т _Ω – драконический период обращения );

• б)    характеристики землеобзора ( ф _з - геоцентрический угол обзора поверхности Земли или

• АХ э – ширина полосы обзора на экваторе).

МЕТОДИКА ОБОСНОВАНИЯ ПАРАМЕТРОВ РЕЗЕРВНЫХ ОРБИТ

Под обзором поверхности Земли понимают наблюдение поверхности Земли с помощью аппаратуры (фото, радио, инфракрасной. телевизионной и др.), установленной на борту КА. Обычно предполагают, что бортовая аппаратура обеспечивает обзор части пространства, ограниченной поверхностью кругового конуса с углом полураствора равным углу обзора бор-

товой аппаратуры у. В этом случае на поверхности шарообразной Земли получаем круговую зону обзора, размеры которой характеризуются геоцентрическим углом ф3 [1], который зависит от радиуса орбиты КА (r ) и угла обзора борто-

I r вой аппаратуры ф ₃ = arcsin l — siny

-Y , где R -

радиус шарообразной Земли. При этом ширина полосы на экваторе равна

AX = 2arcsin f ^s'^ll( P - ) ,

³ I sin e J

где β – угол наклона вектора относительной скорости к плоскости экватора.

Для расчета периодического обзора поверхности Земли используют характеристики трассы полета, в частности, межвитковое расстояние, суточный сдвиг трассы полета КА и др [1, 12].

С учетом влияния нецентральности гравитационного поля Земли абсолютная величина меж-виткового расстояния определяется по формуле

Рассмотрим вопрос об определении максимального разрыва в наблюдении одним КА всей поверхности Земли. Остановимся на случае, когда трасса полета КА пересекает экватор под прямым углом ( β = π /2). Это происходит при наклонении i , ∗ ^,

Х пер          T q

i* = arccos      = arccos — .

∗ эф

При этом наклонении ширина полосы обзора на экваторе с учетом формулы (1) равна

T

AX_mb = 2 n— , MB

■‘ эф

AX = 2Фз

,

где Т _эф – эффективные сутки, время полного оборота Земли относительно восходящего узла

Для определения максимального разрыва в наблюдении одним КА всей поверхности Земли введем величину Δλ

2п орбиты, T =       ; ω – угловая скорость эф ю3-Q    3

вращения Земли, ω _З=7.29·10^–5с^–1; Ω – угловая

–

AX = ^

m

Δλ 2

1 - m

скорость прецессии восходящего узла орбиты, обусловленная влиянием нецентральности гравитационного поля Земли.

Для определения суточного сдвига трассы вводят величину m = { Т _эф / T — }, где {•} - дробная часть числа, тогда абсолютная величина суточного сдвига трассы полета КА определится по формуле

I 2

, если l - нечетно, MB

AX_MB, если l - четно.

Пусть ширина полосы обзора на экваторе меньше величины АХ, т.е AX _э < AX .

Введем величины q j =

j ^AX MB

Δλ

и k j =

j AX mb

Δλ

Пусть l =[^^

AX MB

AX = (1 - m ) AX mb .

целое число оборотов в T

^] = h^^] , где [•] — целая часть T _Ω

сутках

числа,

тогда имеем равенство

^{2 n} = ⁽ l ⁺ m ^{) AX} MB , ИЛИ П = l + m AX mb -

Обозначим k – номер последнего нисходящего узла перед первым восходящим. С учетом формулы (4) после выделения целой части получим

π k = [-

-

AX _MB

Г i

____2

AX mb

] + 1 = ^

, если l - четное,

l + 1

I 2

, если l - нечетное.

Используя величину k_j , можно определить расстояние А Х j между последним ( q j + 1) прохождением экватора на интервале j межвитковых расстояний и j +1 узлом и расстояние ∆ λ′ _j между следующим ( q j + 2) прохождением и j +1 узлом, а именно:

AX j = k j AX = j AX mb - q j AX , j j                   j                  (10)

AX j = (1 - k j ) AX = ( q j + 1) AX- j AX mb -

Определим, вначале, максимальный разрыв в наблюдении одним КА всей поверхности Земли в количестве полусуток П. Рассмотрим частные случаи.

Пусть через q j 1 полусуток выполняются условия AX. < AX₃ , AX’ > AX, (рис. 1).

j 1 ^э j 2 ^э

Абсолютные величины минимальных угловых расстояний образующихся между восходящими и нисходящими узлами в течение половины суток в восточном ∆ λ _вост и в западном ∆ λ _зап направлениях рассчитываются по формулам.

На интервале межвиткового расстояния об-

^AX BOCT

Δλ

зап

= <

1 + m Δλ

m

[ у ^A

1 - m

..„, если l - четно, MB

._MB , если l - нечетно.

^AX MB ,

если l - четно,

разуется q j 1 «окон», которые, начиная с q j 1 + 1

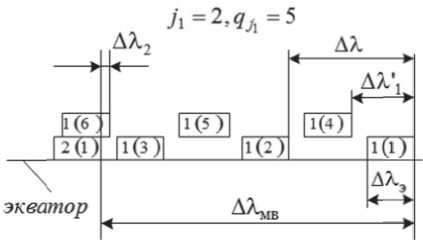
Рис. 1. Расположение полос обзора на экваторе при AX j < AX _э

2- m

I 2

^AX MB ,

если l - нечетно.

полусуток, покрываются по одному в каждые полусутки на величину АХ j . Все межвитковое расстояние будет покрыто полосами обзора, когда выполнится условие АХ j < АХ _э , т.е. через q j 2 + 1 сутки. Итак, величина П может быть определена следующим образом: П = q j 1 + q j 2 +1.

Пусть теперь через q j 2 + 1 полусуток выполняются условия АХ j 2 < АХ э , АХ j 2 > АХ _э(рис. 2).

числа оборотов КА в сутках Т _эф/ T q не фиксированными, запишем уравнения нижних границ области величины П в функции Т _эф j T q .

Например, для величины АХ j 1 в случае нечетного значения l — [ Т _эф / T q ] имеем

^АХ j 1 =

^j i ^АХ мв ^- q j ₁ ^АХ АХ мв     '

^j 1 - q j i

' Г ^Т

2 I Т q

)

- ¹

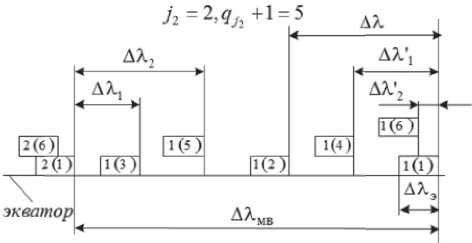
Рис. 2. Расположение полос обзора на экваторе при АХ ' j 2 < АХ э

Аналогичные формулы получим и для случая, когда число l – четн о е [2]. В результате для расчета величин АХ j , , АХ' j ₂ получим

_АХ = | j , - q j , ( Т эф / Т q - 1 )/2, если 1 - нечетно, j ¹    [ j , - q j , ( 1 + 1 - Т эф/ Т q ) /2 , если 1 - четно,

_АХ‘ _— J ⁽ q j ₂ ^{+ 1)( Т} эф/ ^Т Q l V² - j 2 ^{,если 1 - нечетно,} j ²    [( q j ₂ + 1)( 1 + 1 - Т эф/ Т q )/2 - j 2 , если 1 - четно.

Область значений разрыва в наблюдении П ограничивается снизу максимальными значениями величин АХ j , , АХ' j ₂ , а именно:

АХ_э > тах{ АХ j , AX’ j ₂ }.

На пересечении границ имеем равенство

В течение этих q j + 1 полусуток образовались q j 2 + 1 «окно». В дальнейшем каждое «окно» покрывается по одному в полусутки на величину AX j . Полное покрытие всех «окон» произойдет через q j 1 полусуток, когда выполнится условие АХ j 1 < АХ_э. Общее число полусуток опять будет равно П = q j 1 + q j 2 + 1 .

Таким образом, перебирая числа ^j 'b j 2:

^АХ j = ^АХ' j 2 .             (15)

j 1 = 1,2,..., j ₂ = 1,2,..., находим наименьшие, для которых соответственно выполняются условия АХ j 1 < АХ э , Х' j 2 < АХ э и определяем по ним величину наибольшего разрыва в наблюдении в полусутках по формуле

Из этого равенства следует, что сдвиги слева и справа одинаковы и, следовательно, трасса полета через определенное время замкнется, т.е на пересечении границ будет находиться квази-синхронная орбита.

Для нахождения взаимно простых целых чисел p , q , решим уравнение (15) относительно Т _эф / T q с учетом формул (13) и для возможных сочетаний четности и нечетности числа оборотов в эффективные сутки l и числа разрыва, в наблюдении выраженного в полусутках П.

В результате получим.

Для нечетного l:

^П = ^qj ₁ ^{+ q}j ₂ ^{+ 1} .              ⁽¹¹⁾

Перейдем к безразмерным величинам

Δλ         Δλ         Δλ′ j

АХ_Э —   -, ах,- = —j , ^АХ,- = -т—. Следовательно,

АХ _МВ j АХ _МВ j ^АХ _МВ                    ,

p — I q

j 1 + j 2 + 1 П/2

П/2

^{2 ( j} 1 ⁺ j 2 ^{)+ П} l

Для четного l:

Δ λ j

Δλ

— k / - , j АХ мв

AX j — (1 - k j )

Δλ

АХ Мв

Определим область на плоскости числа оборотов КА в сутках ( Т _эф / T q ) и безразмерной Δλ величины ширины полосы обзора АХ _э — ^э , ^АХ МВ

в которой значений числа оборотов П не изменяется. Используя формулы (9, 10, 12) и считая

если П - четно, если П - нечетно.

' ( l + 1 ) П/2 - j1 - jj

P _— I        П/2

q | ( l + 1 ) П - 2 j - 2 j 2

, если П - четно, если П - нечетно.

Среди чисел j_x, j 2 : j_x = 1,2,..., j 2 = 1,2,..., находим наименьшие, для которых соответственно выполняются условий АХ j < АХ_э , АХ' j 2 < АХ э , поэтому в формулах (16,17) числа p , q получаются взаимно простыми целыми числами.

Решив уравнения

AX j i = 0,

AX' = 0, j ₂

с учетом формул (13), найдем граничные значения числа оборотов в сутки Т _эф [Т^ для рассматриваемой области разрыва в наблюдении П.

В зависимости от четности целого числа оборотов за эффективные сутки получим следующую группу формул

Для нечетного l :

7 1 + l q j j²-

„ /7   ,если qji- четно, pi = I    qji /2

q ¹    ——qj³- , если q - - нечетно.

I     qji p 2 =. q 2

^j 2 ⁺ l ⁽ q j ⁺ D/²

• ²       , если q

(qj, + W2

2 j 2 + l (qj + D ----------2----, если q q, +1              32

j 2

- нечетно,

- четно.

Для четного l :

-—q--j ,если q; - четно, pi = J    qjJ2*

q¹   (--- ^---j .если q - нечетно.

[ qj

P 2 = . q 2

( l + 1)( q j ₂ + 1)/2 - j 2

(qj 2 +1)/2

( l + 1)( qj ₂ + 1) - 2 j i ^qj 2 ^{+ 1}

, если q j ₂

, если q j ₂

- нечетно, - четно.

В приведенных формулах в числителях приведены выражения для величины p , в знаменателях – для q с учетом их взаимной простоты. На рис. 3 приведена область разрыва в наблюдении.

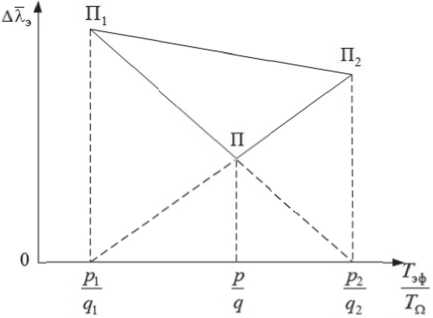
Рис. 3. Область разрыва в наблюдении

Между областями разрывов в наблюдении, используя формулы (16-20) можно установить следующие связи: П = П + Щ и т.д. [2].

Обозначим через ∆t1 – разрыв в наблюдении всей поверхности Земли, выраженный в коли- честве периодов обращения КА TΩ. Величина его в каждой области по числу периодов будет одинакова, так как одинаково значение П. Рассмотрим случай, когда орбиты являются квази-синхронными.

В зависимости от четности чисел p и q нисходящие узлы по-разному располагаются относительно восходящих узлов.

Определим минимальное угловое расстояние между восходящими узлами за q суток AX min . Так как за это время КА совершает ровно p оборотов, то на экваторе равномерно размещается p восходящих узлов и поэтому AX' min = 2 л/ p . Угловое расстояние между восходящими и нисходящими узлами на первом витке равно л + АХ _мв/ 2 . Следовательно, на этом интервале укладывается ( д + АХ мв/ 2 ) / АХ'_тш = ( q + p )/2 угловых расстояний AX' min • Откуда получаем, что при нечетных значениях чисел p , q – восходящие узлы совпадают с нисходящими узлами. Минимальное расстояние (не равное нулю) между узлами AX min = AX m^ = 2 п/ p (рис. 4).

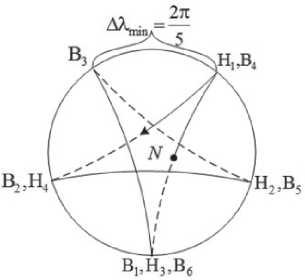
Рис. 4. Трасса полета за время

A t 1 = ( p + 1 ) Г _П / 2 для орбиты q = 1, p = 5

Если же одно из чисел q или p четно, то с учетом их взаимной простоты получаем, что (q + p)/2 не является целым числом. Восходящие узлы не совпадают с нисходящими узлами, а располагаются от них на угловом расстоянии AX   =(q+p-Гq+p 1)лг. = AX'min = il min ^ 2       2 min 2 p

(рис. 5).

Таким образом, для квазисинхронных орбит минимально возможное расстояние между узлами равно

АХ

min

2 л/ p , если q • p - нечетно, л/ p , если q • p - четно.

Если ширина полосы обзора находится в пределах АХэ е [ AXmin, 2AXmin), то время разрыва в наблюдении поверхности Земли вычисляется по формулам

A t₁

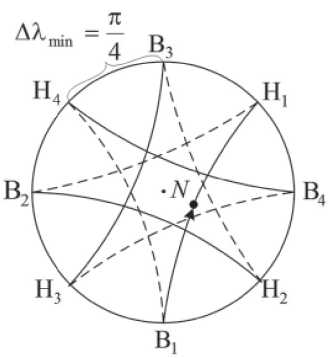
Рис. 5. Трасса полета за время A t i = pT ^ для орбиты q = 1, p = 4

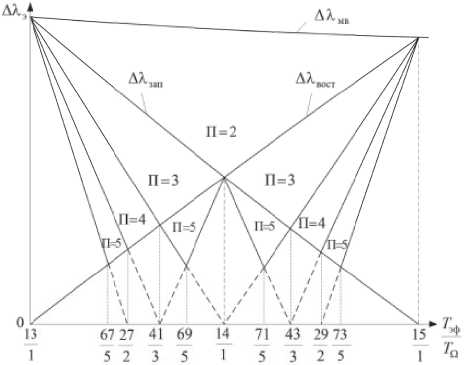
Рис. 6. Области разрывов в наблюдении

A t₁

Р + U Т" ^{t q ,}

если q • p - нечетно,

pT _Q , если q • p - четно .

С учетом (19-20) получим

П₇ 1 l +

2   2

T q + ( j₁ + j 2 ) T q , если 1 - нечетно,

=

2( 1 + « + 2

T q - ( j i + j 2 ) T q , если 1 - четно.

Если AX _э <  AX _min , то периодический обзор всей поверхности Земли невозможен. Орбиты, на которых периодический обзор не возможен, называются критическими. Условиями критичности орбит будут их квазисинхронность и наличие ширины полосы обзора, меньшей минимального расстояния между узлами [2,13].

Если AX _э = AX _min , то полосы обзора располагаются на экваторе встык друг к другу. То есть используется вся ширина полосы обзора. В этом случае орбиты называются оптимальными. Таким образом, условиями оптимальности орбит

являются их квазисинхронность и равенство ширины полосы обзора минимальному расстоянию между узлами [2]. На рис. 6 показаны области значений величины П в случае, когда AX _э < AX _мв .

Как видно из рисунка, при каждом значении величины П минимальное значение ширины полосы обзора соответствуют отношению

£Эф = p

T Ω   q

квазисинхронных орбит, лежащих на

пересечении нижних границ в каждой области.

ПРИНЦИПЫ ПОСТРОЕНИЯ СИСТЕМЫ КА ПЕРИОДИЧЕСКОГО ОБЗОРА

Системы КА периодического обзора как правило строят по изомаршрутному способу [2,12], когда КА системы следуют друг за другом по од-

ной трассе полета. Обозначим через AX _э ширину полосы обзора при наличии в сист ⁿ еме n КА. При наклонении i = i * и квазисинхронной

ТЭФ Р орбите = ширина полосы обзора равна TΩ  q

Δλ

э

2п

— , если q • p - нечетное,

p

π

, если q • p - четное.

p

При n= 1 время разрыва в наблюдении равно

A t₁ = <

Р ^{+ 1} rp ^T ^t q ,

если q • p

- нечетно,

p T q , если q • p - четно.

Если вдоль участка трассы полета КА, образуемого при его движении за время ∆ t ₁, разместить равномерно n КА, т.е. n КА будут следовать по одной трассе через интервал времени

a ti

A t n =    , то время разрыва в наблюдении всей

n поверхности Земли уменьшится в n раз, по сравнению с ∆t1 и будет равно ∆tn.

Положение КА по прямому восхождению восходящего узла орбиты Ω и по аргументу широты КА u можно определить следующим обра-

A t зом. Так как A tn = —1, то

n

2п

Ω = Ω +   Δt i         i 1 rp        n

^ эф

2п .

ui = ui - 1 - ^^A tn • T _Ω

Для получения резервных орбит из всего множества квазисинхронных орбит следует остановиться на орбитах с периодом обращения меньшим, чем период обращения на штатной орбите, и обеспечивающих ширину полосы

обзора в пределах АХ _э е [ АХ _min , 2 АХ _min ) . Кроме этого, для этих орбит разрыв в наблюдении в числе полусуток должен быть по возможности равен разрыву в наблюдении на штатной орбите. Если ширина полосы обзора уменьшится так, что орбита станет критической, то разрыв в наблюдении в числе полусуток может быть увеличен для перехода к новой квзисинхронной орбите обеспечивающей ширину полосы обзора в пределах АХ _э е [ АХ _min, 2 АХ _min).

При проектировании систем КА в качестве показателя результативности используют набольшее время разрыва в наблюдении [2,12,14]. Поскольку период обращения КА на резервной орбите будет меньше периода обращения КА на штатной орбите, то величина максимального разрыва в наблюдении при использовании резервных орбит будет равна максимальному разрыву в наблюдении при отсутствии одного КА на штатной орбите. Поэтому результативность решения целевых задач будем характеризовать средним значением разрыва в наблюдении всеми КА системы на штатных и резервной орбитах точек на поверхности Земли - А t _ср.

Рассмотрим алгоритм получения квазисин-хронных резервных орбит. Пусть число оборотов КА в сутках лежит в пределах Т _эф (Т — е [ l ₁, l ₁ + 2] , (при необходимости диапазон числа оборотов КА в сутках может быть расширен) где l ₁ – нечётное целое число из диапазона возможных значений числа оборотов в сутки [1,16]. Будем перебирать последовательно значения разрыва в наблюдении в полусутках П в сторону уменьшения, начиная со значения П на штатной орбите. Для каждого значения разрыва в наблюдении в полусутках П определяем число эффективных суток, через которые трасса полёта замыкается

[ П, если П - нечетное, q-1 П н

—, если П - четное.

[ 2

Тогда из возможных значений числа оборотов в каждых сутках в указанном диапазоне p = ql1 + 1,..., q l1 + 2q -1, оставляем только взаимно простые числа p, q и в зависимости от четности или нечетности числа П такие, у кото- рых p ⋅ q – нечётное, если П – нечётное и p ⋅ q – чётное, если П – чётное. Отобранные орбиты проверяем на выполнение условия не критичности АХэ е [АХmin,2АXmin). При необходимости увеличения количества резервных орбит или при попадании на критическую орбиту значение П последовательно может увеличиваться на единицу необходимое количество раз.

ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ МЕТОДИКИ

Пусть система КА наблюдения Земли, состоящая из 3 КА, построена изомаршрутно на г      ТэФ 67 _ _     _ квазисинхронных орбитах — с наклоне-T—   5

нием орбиты i =88^°, с шириной полосы обзора АХ _э е [ АХ _min, 2 АХ _min ) , АХ _min = 5,37^о и значением П=5, обеспечивающих обзор всей поверхности земли с наибольшим разрывом в наблюде-

Л    34 То нии А л, -   —.

• ³     3

Для значения разрыва в наблюдении П=5 в диапазоне числа оборотов КА в сутках T

• — е [ 13,15 ] квазисинхронными орбитами будут т —

орбиты со значениями числа оборотов в сутках, определяемыми следующими отношениями чи-

67 69 71 73

сел p,q : —, —, —, — ( рис. 6). Если система

5   5                          67

КА построена с использованием орбиты —, то орбиты ^, -у-, -у могут рассматриваться как резервные. В табл. 1 приведены параметры штатной и резервных орбит, где обозначено: высота орбит H, максимальный разрыв времени в наблюдении одним КА поверхности Земли Δt1 в числе драконических периодов обращения, ширина полосы обзора на экваторе Δlэ, угол обзора бортовой аппаратуры γ , драконический период TΩ .

В табл. 2 приведены значения средних разрывов в наблюдении Δ t _ср системой КА точек на

Таблица 1. Параметры штатной и резервных орбит КА системы наблюдения Земли

Параметры квазисинхронной орбиты	H , км	А 1 1	АХ Э		T — , c
			7 =20 °	Y =22 °
p=67, q=5	1101	34T —	7,3	8,1	6428
p=69, q=5	953	35T —	6,34	7,1	6242
p=71, q=5	814	36T —	5,41	6,01	6066
p=73, q=5	682	37T —	4,53	5,0	5899
p=44, q=3	664	44T —	4,39	4,9	5872

Таблица 2. Параметры наблюдения поверхности Земли системой КА

Состав системы КА Параметры квазисинхронной орбиты Atср, с 7-20° Y-22° 3 штатных КА р-67, q-5 4189 3590 2 штатных КА р-67, q-5 6294 5398 3 КА (2 штатных КА, 1 КА на резервной орбите) р-69, q-5 4513 3857 3 КА (2 штатных КА , 1 КА на резервной орбите) р-71, q-5 4854 4120 3 КА (2 штатных КА , 1 КА на резервной орбите) р-73, q-5 - 4388 3 КА (2 штатных КА , 1 КА на резервной орбите) р-44, q-3 5163 - всей поверхности Земли по результатам моделирования наблюдения поверхности Земли системами КА различного состава при двух значениях угла обзора бортовой аппаратуры γ.

В качестве вариантов состава систем приведены: полный состав из 3 КА, неполный состав при отсутствии одного КА и составы из 3 КА при нахождении одного КА на соответствующей резервной орбите. При значениях чисел p=73, q=5 и при значении γ =20° орбита становится критической, поэтому получена резервная орбита со

T -Ф _ 44 значением П=6 с параметрами —- - —.

T Q ³

При использовании резервных орбит величина Δ t _ср постепенно увеличивается с уменьшением высоты резервной орбиты, но остается меньше значения Δ t ₁ при отсутствии одного КА в системе. Величина максимального разрыва в наблюдении во всех вариантах резервных орбит равна максимальному разрыву в наблюдении при отсутствии одного КА на штатной орбите, однако она наступает значительно реже, в том случае, когда плоскость резервной орбиты за счёт прецессии совпадает с плоскостью КА на штатной орбите. При отсутствии одного КА на штатной орбите максимальный разрыв в наблюдении достигается ежесуточно.

ЗАКЛЮЧЕНИЕ

Полученные результаты позволяют сделать вывод, что КА, запускаемые в нештатных ситуациях на резервные орбиты, влияют на характеристики просмотра территории земного шара. Практически сохраняются средние значения величины разрыва в наблюдении всей поверхности Земли. При этом обзор поверхности Земли будет не столь равномерным как на штатных орбитах. И, хотя величина максимального разрыва в наблюдении при использовании резервных орбит равна максимальному разрыву в наблюдении при отсутствии одного КА на штатной орбите, достигается она значительно реже. Так как принятие решения на выведение КА на резервную орбиту в ряде случаев принимается автономно во время полёта СВ, то эти орбиты КА должны быть определены до старта, а их параметры заложены на борт СВ.