Обоснование параметров рыхлителя почвообрабатывающей машины стратификатора

Механическая обработка почвы сельскохозяйственными машинами и орудиями ориентирована на улучшение условий роста и развития растений [1]. Современные мировые требования получения безвредных для организма человека продуктов питания требуют отказа от химических средств контроля за сорняками при выращивании сельскохозяйственных культур.

Почвообрабатывающая машина стра-тификатор (рис. 1) оптимизирует физико-механическое состояние обрабатываемого слоя почвы на глубине до 18 см [2–4], является прицепным универсальным агрегатом для выполнения предпосевной и основной поверхностной обработки почвы, при которой сорняки бережно извлекаются вычесыванием вместе с цельной корневой системой и укладываются на поверхность,

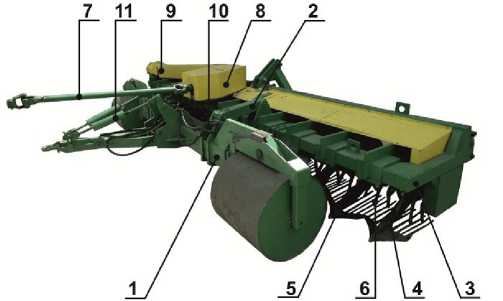
Р и с. 1. Машина почвообрабатывающая рыхлительно-сепарирующая ПРСМ-5:

1 – шасси; 2 – рычажный механизм; 3 – рама; 4 – стойка; 5 – плоскорежущая лапа с сепарирующими решетками; 6 – ротор с рыхлителями; 7 – карданная передача;

8 – зубчатая передача; 9 – цепная передача; 10 – механизм регулировки глубины обработки почвы;

11 – механизм регулировки горизонтального положения рамы [7]

F i g. 1. The PRSM-5 tilling and separating machine: 1 – the chassis; 2 – the lever mechanism;

• 3    – frame; 4 – the rack; 5 – ploughshare with separating gratings; 6 – rotor with rippers; 7 – cardan gear;

• 8    – a gear transmission; 9 – chain transmission; 10 – mechanism for adjusting the depth of tillage;

• 11    – mechanism for adjusting the horizontal position of the frame

где они высушиваются под воздействием климатических факторов [5–7].

Машина (рис. 1) состоит из шасси 1 , с которым посредством параллелограм-много рычажного механизма 2 с возможностью перемещения по вертикали закреплена рама 3 . На ней смонтированы пассивные (стойки 4 с лемехами 5 ) и активные (ротор с рыхлителями 6 ) рабочие органы таким образом, что ротор расположен над лемехами и не касается их. Лемеха снабжены сепарирующими решетками [3; 4; 7].

Исходя из условий прорастания и развития растений, конструкция оптимального обрабатываемого слоя (рис. 2) перед посевом должна состоять из четырех подслоев: надсеменного, семенного, подсеменного и подпахотного. Из надсеменного подслоя должны быть полностью исключены глыбистые отдельности почвы размером более 20 мм. В семенном подслое должна быть сосредоточена наиболее ценная в агрономическом отношении структура. Плотность сложения подсеменного подслоя не должна превышать 1,25 г/см3. Подпахотный подслой не должен иметь плотность выше 1,3 г/см3 и твердость в плужной подошве более 3 МПа, что обеспечивается основной обработкой [5; 7].

Создание указанных условий обеспечивает контакт семян с почвой, быстрое прорастание и беспрепятственное развитие корней вглубь почвы [6].

При движении машины по полю лемеха поднимают слой почвы, далее при перемещении вдоль поверхностей лемеха и прутьев сепарирующей решетки происходит его крошение, при этом мелкокомковатая фракция просыпается сквозь решетку, формируя семенной подслой. Дальнейшее формирование семенного подслоя происходит с помощью рыхлителей ротора, которые крошат и рыхлят почву, перемещая ее вдоль сепарирующей решетки. Крупнокомковатая фракция с отдельностями не более 20 мм движется сходом с решетки, образуя надсеменной подслой. Кроме этого, рыхлители ротора в процессе

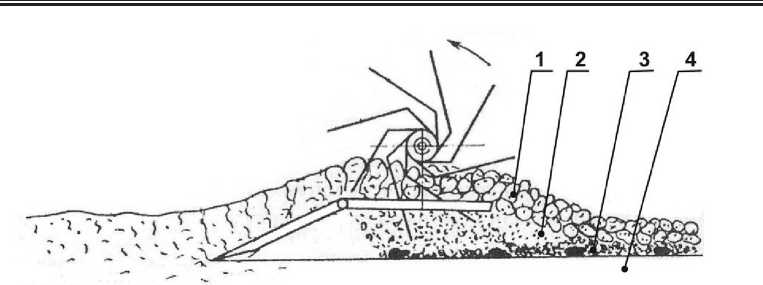
Р и с. 2. Структура обрабатываемого слоя: 1 – надсеменной слой; 2 – семенной слой;

3 – подсеменной слой; 4 – подпахотный слой [7]

F i g. 2. Structure of the processed layer: 1 – the above seed layer; 2 – the seed layer;

3 – sub seed layer; 4 – sub-plow layer

взаимодействия с почвой вычесывают из нее сорные растения, не нарушая их целостности, и транспортируют их на поверхность надсеменного подслоя [7].

При взаимодействии рыхлителя ротора с почвой происходит формирование почвенного ядра, установившееся движение почвы по лемеху и сбрасывание ее с сепарирующей решетки. Наихудшие условия для движения почвы в технологическом процессе работы машины создаются в момент входа рыхлителя в почву, что является причиной образования перед ним почвенного валка. Он способствует повышению энергоемкости процесса, снижению надежности и качества работы машины [8; 9]. Около 30 % от общих затрат энергии в процессе работы машины расходуется на привод ротора, поэтому она неудовлетворительно работает на плотных почвах, а следовательно, ее использование в таких случаях становится малоэффективным [9].

В связи с указанными недостатками машины параметры рыхлителя ротора должны быть обоснованы с учетом снижения затрат энергии на его привод.

Обзор литературы

Снизить энергоемкость процесса работы ротора почвообрабатывающей машины в нашем случае возможно за 260

счет совершенствования геометрической формы его рабочих органов-рыхлителей [9–12].

Для получения закономерности распределения давлений почвы на поверхности рабочего органа решалась контактная задача с использованием теории сплошных сред [13; 14]. В процессе воздействия рабочего органа на почву ее пластическое движение по некоторой плоскости начинается только тогда, когда касательные напряжения на поверхности скольжения достигают критических величин. Рабочий орган, имеющий главные оси симметрии, представлялся в виде двух плоских сечений. Почва рассматривалась как линейно деформируемая среда. Затем решения двух плоскостных задач объединялись и получались зависимости распределения давлений по поверхности почвообрабатывающего рабочего органа. Общее решение уравнения контактной задачи описывается следующим образом:

P (x)

sin ли sin ли

Л

f'( x ) -

cosл2и       Ц+Y

--( a + x ) ² P, л

Технологии и средства механизации сельского хозяйства

где γ – коэффициент, зависящий от твердости почвы; /' ( x ) - уравнение линии, описывающей профиль деформатора; υ – скорость движения, м/с;

C t

P = J P ( t ) dt - сжимающая сила, Н.

- C

С помощью решения контактной задачи получены закономерности распределения давления на границе рабочего органа с почвой для плоского, круглого, клиновидного и эллиптического деформаторов.

Решение контактной задачи в земледельческой механике обеспечивает обоснование формы деформатора с требуемым распределением давления. Такой подход, по мнению авторов, позволяет с достаточной для практики точностью конструировать катки и колеса, обеспечивающие равномерное распределение давления в зоне их контакта с почвой.

В исследованиях по изысканию профильной линии почвообрабатывающего рабочего органа минимальной энергоемкости теоретическим путем определялось силовое воздействие почвы на рабочий орган [15; 16]. При этом процесс рассматривался как квазиста-ционарный с постоянными скоростью движения и расстоянием от центра масс рабочего органа до плоскости микронеровностей поверхности почвы. В связи с последним полагалось, что главный вектор системы сил сопротивления динамическому напору в среднем можно считать величиной постоянной, то есть независимой от времени.

Давление почвы на поверхность рабочего органа рассматривалось как результирующее статической и динамической составляющих1. Приведено доказательство изотропности закона внутрипочвенного статического нормального давления, в результате чего установлено, что в каждой точке почвенного горизонта напряжение сил зависит не от ориентации площадки, а только от глубины ее расположения.

В неподвижном состоянии рабочий орган испытывает только силы внутреннего статического давления [17]. С началом движения к ним присоединяются силы динамического напора, или, как их называют авторы работы, силы импульсного давления, которые возникают в результате столкновения рабочего органа с частицами почвы. По утверждению авторов, экспериментальные исследования показали, что соударение частиц почвы с рабочими органами является практически неупругим, так как они имеют очень малый коэффициент восстановления. В таком случае при ударе нормальная составляющая скорости движения частицы почвы относительно рабочего органа равна нулю, а сохраняется только касательная составляющая [18–20]. Поэтому авторы считают, что в системе динамических сил сопротивления при соударении с рабочими органами возникают потери нормального импульса почвенных частиц к рабочей поверхности. Это подтверждает известное положение о нормальном направлении сил динамического давления к рабочей поверхности [21; 22].

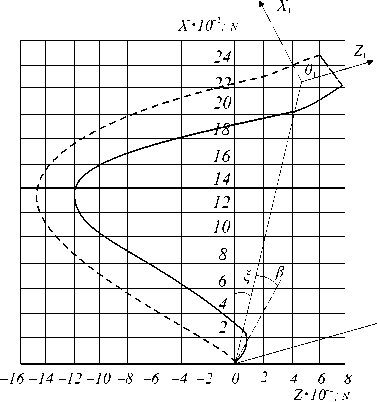
Нормальное динамическое давление зависит только от глубины расположения в почве элементарной площадки и ее пространственной ориентации и не зависит от формы остальной части рабочего органа. За промежуток времени dt частицы почвы, со стороны которых элементарный участок испытывает импульс силы, заполняют косой цилиндр. Из этих предпосылок с помощью закона сохранения количества движения получено уравнение для определения напряженных сил суммарного нормального давления почвы на поверхность рабочего органа в точке М:

P(M) = P0 (M) + pu2cos2 a(M\ (2)

где Р ( М ) – сила внутрипочвенного статического нормального давления, Н; ρ – плотность почвы, кг/м³; α ( М ) – угол, определяющий пространственную ориентацию элементарной площадки рабочего органа.

Вывод уравнения проводился без предположений о скорости, в связи с чем формула (2) справедлива не только для квазистационарного движения.

На основании уравнения (2) выведена формула для определения динамического сопротивления:

л

fl y (M) Q = pu 11 —-—-' I a .

cos³ a ds,   (3)

где у ( М ) – координаты точки М (рис. 3).

Предполагается, что формула (3) применима для вычисления динамического сопротивления любого рабочего органа почвообрабатывающего орудия.

Р и с. 3. График динамического давления почвы на рабочий орган [13]

F i g. 3. Diagram of dynamic soil pressure on the implement

Для решения конкретной задачи по обоснованию профильной линии рабочего органа минимальной энергоемкости динамическое давление вычисляется по формуле:

xk     V ^ V '3

Q = bpu J 1 -        dx,   (4)

0 I a J1 + V^

где b – ширина рабочего органа, м.

Следовательно, величина нормального давления почвы на элементарную площадку поверхности рабочего органа определяется квадратом скорости его движения, плотностью почвы, глубиной расположения и пространственной ориентацией площадки. Однако полученное уравнение не учитывает физико-механических свойств почвы (за исключением плотности), которые весьма существенно влияют на энергетические показатели рабочих органов почвообрабатывающих орудий. Это связано с тем, что при выводе уравнения (3) учитывалось только взаимодействие частиц почвы с рабочим органом и не было учтено взаимодействие частиц между собой. На них влияют физико-механические свойства почвы. Последнее можно объяснить сложностью процессов, происходящих в почве под воздействием рабочего органа. Их формализация в настоящее время затруднена. Кроме того, необходимо экспериментально проверить, что влияние на величину динамического давления, на элементарную площадку рабочего органа, а также на остальную его форму отсутствует. Также важно тестирование степени адекватности полученной модели в реальных условиях.

Материалы и методы

С использованием векторного и тензорного исчислений процесс нагружения почвы рассматривался как последовательность равновесных состояний и малых деформаций, компоненты тензора которых связаны с проекциями вектора перемещения соотношениями Коши [23–25]. Решение задачи о деформациях и напряжениях в почве, возникающих в результате действия на него клина, осуществлялось с учетом физических законов взаимосвязи компонентов напряжений и деформаций [26]. Почва рассматривалась как упруго-пластическая среда, при работе с которой применялись модель обобщенного закона Гука и один из вариантов теории пластического течения [27; 28]. С целью экономии объема вычислений использовались сведения из ряда исследований [29; 30], а в процессе счета определялась интенсивность напряжений, при которых происходит отрыв, полипластические деформации поверхности, расчленения слоя грунта на глыбы [31–33]. Была построена математическая модель определения напряженно-деформируемого состояния слоя почвы под воздействием клина, обеспечивающая определение полей векторов перемещений, тензоров деформаций и напряжений. Для численного решения задачи использовался метод Ритца [34–36]. Разработан алгоритм решения поставленной задачи, позволяющий определить поля напряжений и деформаций в упругой области слоя почвы и указать границы области начала пластических деформаций.

Энергетические показатели функционирования рабочих органов почвообрабатывающей машины оценивались тяговым сопротивлением и крутящим моментом привода ротора рыхлитель-но-сепарирующего устройства. Общее тяговое сопротивление почвообрабатывающего рабочего органа состоит из суммы проекций горизонтальных сил (удельных сил сопротивления) на плоскость (по аналогии с составляющей силы сопротивления лемеха, выраженной В. П. Горячкиным через квадрат скорости движения лемеха в почве). Суммарная составляющая сила определялась с помощью тензометрической аппаратуры по общеизвестным методикам с относительно небольшими затратами труда и времени. В связи с этим методом определения закономерности распределения давления почвы на поверхности рабочего органа являлась аппроксимация результатов экспериментальных исследований по отысканию суммарных сопротивлений его составных частей.

Результаты исследования

Для решения задачи по усовершенствованию геометрической формы рыхлителя полагаем, что ротор вращается с постоянной частотой, а почва представляет собой однородную среду. Элементарная площадка рабочей кромки рыхлителя (рис. 4) подвергается действию сил трения между кромкой и почвой qfdl и боковой поверхности рыхлителя о почву, а также влиянию давления почвы qdl . Величина силы трения боковой поверхности рыхлителя о почву не оказывает существенного влияния на сопротивление движению рыхлителя в почве и поэтому ею можно пренебречь.

Элементарный крутящий момент ротора определяется по уравнению:

dM = qp ( sin в + cos в ) dl, (5) где ρ – радиус вращения элементарной площадки, м; θ – угол между нормалью к радиусу вращения элементарной площадки и направлением действия нормальной силы [9].

Закономерность изменения давления почвы на рыхлитель, в зависимости от глубины расположения в почве его элементарной площадки, определена экспериментальным путем:

q = kh^m , (6)

где h – расстояние от проходящей по поверхности плоскости до элементарной площадки, м; k , m – коэффициенты,

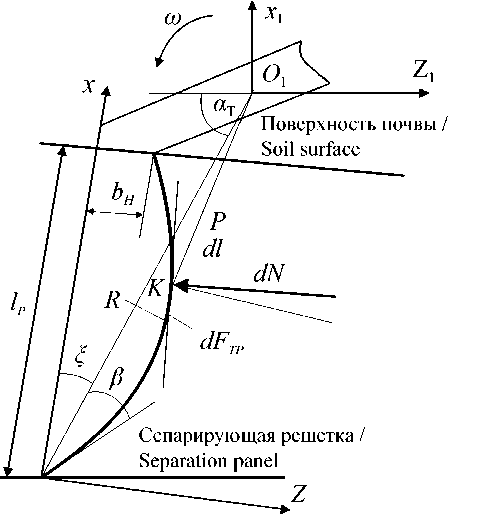
Р и с. 4. Схема к обоснованию формы рабочей кромки рыхлителя ротора [9; 11]

F i g. 4. The scheme to substantiate the shape of the working edge of the ripper of the rotor

зависящие от влажности и твердости почвы.

Процесс работы рыхлителя рассмотрен в подвижных осях системы координат XOZ (рис. 4). В принятой системе координат расстояние от элементарной площадки до поверхности почвы определяется по уравнению:

k ₁ – коэффициент, обусловленный расстоянием от слоя почвы на решетке до оси вращения ротора.

С учетом того, что dl = ^1 + z 2 dx , заменив косинус и синус через тангенс угла θ , на основании соотношения (5) получим уравнение для вычисления крутящего момента рыхлителя ротора:

,          1

h = ।-----1

4 1 + k

[ k , sin ( a _T + a , ) - cos ( a _T + a , ) ] x -- [ sin ( a _T + a , ) + k , cos ( a _T + a , ) ] z + [ , + R ( cos a T - k , sin a T ) + b

xk

M-/ xh

q p ( 1 + tg Q ) 71 + ^z 1 1 + tg² 9

dx .

Для наиболее весомого сниже-

где R – радиус ротора, м; α _Т – угол поворота рыхлителя в текущий момент времени; α ₁ – угол между радиус-вектором носка рыхлителя и осью координат OX ; b – коэффициент, обусловленный высотой слоя почвы на решетке;

ния усредненного крутящего момента и уменьшения неравномерности вращения ротора необходимо добиться уменьшения максимальных значений указанного крутящего момента.

В связи с изложенным постановка задачи формулируется следующим образом. Из множества кривых,

Технологии и средства механизации сельского хозяйства

проходящих через точки ( x_h , z_h ) и ( x_k , z_k ), необходимо найти ту, при которой крутящий момент рыхлителя во время входа его в межпрутковое пространство сепарирующей решетки будет иметь минимальное значение. Для решения поставленной задачи воспользуемся методом Ритца. Уравнение кривой, обеспечивающей экстремальное значение функционала, имеет вид:

2 z x Za z = xz 0 + x——2-^-0 + xk

+ ( x - x_k ) ( C 1 x - C 2 x ² + C 3 x ³ ) , (9)

где z' ₀ – тангенс угла между осью OX и касательной к кривой в начальной его точке.

Для данного рыхлительно-сепариру-ющего устройства z' ₀ выбирается из условий максимально возможного захвата почвы в начальный момент ее взаимодействия с рыхлителем, что позволяет снизить сгруживание почвы перед ротором [23; 25]. Из рисунка 4 видно, что z' ₀ = = tg( α ₁ + β ₁), где β – угол между радиус-вектором носка рыхлителя и касательной к кривой в этой же точке.

Подставив выражение (9) в уравнение (8), находим значение коэффициентов С ₁, С ₂, С ₃, с помощью которых определяется форма рыхлителя. Приравняв к нулю частные производные от полученного уравнения по С ₁, С ₂, С ₃, получаем систему уравнений:

dp

, dz z--R sincz, dCi         1

d x dct

^dC i ^R² - 2 R ( z sin^ + x cos « J+ z² + x²

a q ₌ _ k, _ _n h - 2 sin ( « T + « 1 ) + k i cos ( « + « 1 ) ap a c    ^{( )}           Vu k ²        a c’

[ z '( R sin a , - z ) + R cos a 1 - x J x

x ( R cos a 1

^^^^^^B

9 tg 9

9 C i

= < — Rz sin a T

x

x 9 z 9 z ' x )--- +---

’ 9 C i 9 C i _

—

x ^ z '( R cos a 1 — x ) — R sin a 1 + z J x

9 z    9 z^'

x — z

9 C_i    9 C_i

x [ z '( R sin a 1 — z ) + R cos a 1 — x J ,

2x z = z0 + 2(zk -xkz0)+ xk

' x - x_k )( 2 xC 1 + 3 xC 2 + C ₃ ) +

+ x ² C 1 + x ³ C ₂ + xC₃,

а м 0i ₌ a C i

где i = 1,2,3.

⁺ |

+ q

q ( 1 + z ') ² ( tg² ° - 1 ) | | +

( 1 + z ') 2 ( f tg ° - 1 )| q +

(               A z'(f td0-l)x л1 az'

^{x( 1 + z} ^² a C+ + ( 1 + z ^ ^ V           ^a C i ;

где z-^-=x2 (x-xk); z-^-=x3 (x-xk);

9C1     V k! 9C2

9 z

----= x I x - x ,) ;----= 2 xlx - x, )+ x ^z;

9C3    V k! 9C1

9 z' 2 -, з

----= 3 x x - x, + x ;----= ( x - x , 1 + x .

9C2      V k7      9C3 vk’

Полученную систему уравнений (10) решали численным методом. Расчеты проводились при R = 0,23 м; k = 4 000; n = = 1,99 Н/м²; k ₁ = –4; B = –0,1; α _т = 60°; α ₁ = = 12°; f = 0,5; z 0 = 0,9; B_A = 0,03 м; P = = 0,2 м.

В результате решения системы уравнений получены значения коэффициентов С ₁, С ₂, С ₃. С их учетом уравнение получает вид:

z = 0,8 x - 32 x ² + 144 x 3 .       (11)

Линия, определяющая геометрическую форму рыхлителя ротора, согласно уравнению (11), показана на рисунке 5.

Р и с. 5. Форма рыхлителя ротора рыхлительно-сепарирующего устройства

F i g. 5. The shape of the ripper of the rotor of the ripping-separating device

Энергетические показатели работы секции почвообрабатывающей машины с рыхлителями ротора обоснованной формы (рис. 6) оценивались крутящим моментом привода ротора рыхлитель-но-сепарирующего устройства.

Крутящий момент привода ротора определялся для рыхлителей с ровным (базовым), выпуклым, вогнутым и обоснованным с учетом снижения затрат энергии в результате проведения теоретических исследований профилем. Рыхлители с различным профилем режущей кромки приведены на рисунке 7.

Проведение эксперимента осуществлялось при частоте вращения ротора 2,5 с^–1 и влажности почвы 21,5 %. Результаты эксперимента приведены в таблице. Среднеквадратичная ошибка опыта составила 0,44 Н ⋅ м, достоверность результатов 99 %.

Обсуждение и заключение

Обоснованный с учетом снижения затрат энергии профиль рыхлителя ротора обеспечивает наилучшие условия

Р и с. 6. Машина почвообрабатывающая рыхлительно-сепарирующая ПРСМ-5 с рыхлителями ротора обоснованной формы

F i g. 6. The PRSM-5 tilling and separating machine with rotor rippers of reasonable shape

266                                   Технологии и средства механизации сельского хозяйства

Р и с. 7. Рыхлители с различной формой рабочей кромки: 1 – ровная; 2 – выпуклая;

3 – вогнутая; 4 – обоснованная с учетом снижения затрат энергии

F i g. 7. The rippers with different cutting edge shapes: 1 – flat; 2 – convex;

3 – concave; 4 – justified considering the reduction of energy costs

Т а б л и ц а

T a b l e

Крутящий момент привода ротора для различных форм его рыхлителей Rotor drive torque for different ripper shapes

№	Профиль ножа / Knife profile	Крутящий момент, Н ⋅ м / Torque, N ⋅ m
		средний / medium	максимальный / maximum

1 Ровный / Plain 12,26 23,10 2 Выпуклый / Convex 13,02 31,46 3 Вогнутый / Concave 11,56 25,03 4 Обоснованный с учетом снижения затрат 8,39 20,85 энергии / Justified in terms of reduced energy costs для транспортирования почвы в начальный момент вхождения в почву и минимальные затраты энергии на привод. Такую форму рыхлителя ротора можно использовать для машины, обеспечивающей оптимизацию агрофизического состояния посевного слоя почвы при посеве семян пропашных культур или перед посевом, когда сорные растения находятся в начальной стадии своего развития.

В одну из задач технологического процесса машины для оптимизации пахотного слоя почвы входит вычесывание корневищ сорных растений и выбрасывание их на поверхность поля.

Для такой машины профиль рыхлителя должен быть обоснован с учетом уменьшения возможности забивания ротора пожнивными остатками и сорными растениями. При относительно небольшой частоте вращения ротора машины и достаточной длине рабочей части рыхлителя растительные остатки могут задерживаться, совершать колебательные движения или сходить с него. Для достижения последнего угол наклона наиболее пологой касательной к профилю рыхлителя в самом неблагоприятном его положении должен обеспечить условия сползания растительных остатков.

Q ИНЖЕНЕРНЫЕ ТЕХНОЛОГИИ И СИСТЕМЫ Том 31, № 2. 2021

Поступила 23.01.2021; одобрена после рецензирования 15.02.2021; принята к публикации 01.03.2021

Автор прочитал и одобрил окончательный вариант рукописи.

270 Технологии и средства механизации сельского хозяйства