Обоснование применения формулы давления идеального газа при выводе уравнения Леонтьева для параметра Грюнайзена твердых тел

Параметр Грюнайзена служит характеристикой ангармонизма колебаний решетки и обычно вычисляется по уравнению Грюнайзена из экспериментальных данных о коэффициенте объемного теплового расширения β, изотермическом модуле объемного сжатия В, молярном объеме V и молярной теплоемкости C V [1]

Y = ev_ . c

C _V

Это соотношение выводится из уравнения состояния.

Леонтьев [1] выполнил усреднение частоты колебаний решетки ω и непосредственно из определения γ = – d lnω/ d ln V получил следующее уравнение для параметра Грюнайзена

Г в

Y = — —-2 I pv

A ) ’

K J

где В А – адиабатический модуль всестороннего сжатия, ρ – плотность, v K – среднеквадратичная скорость звука, которая не зависит от направления распространения волн:

2 v 2 + 2 v 2 v 2 = —------,

K 3

v S и v L – скорости продольной и поперечной акустических волн .

Формула Леонтьева привлекательна тем, что в отличие от уравнения Грюнайзена она позволяет рассчитывать γ по доступным экспериментальным данным о плотности и упругих характеристиках. Однако ни самим автором, ни другими исследователями эта формула не сравнивалась с уравнением Грюнайзена, она была использована для других целей [1].

Настоящая работа посвящена непосредственному сопоставлению уравнений Леонтьева и Грю-найзена, а также обсуждению одного допущения, использованного при выводе формулы Леонтьева. Предлагается расчет γ по этой формуле для стеклообразных систем.

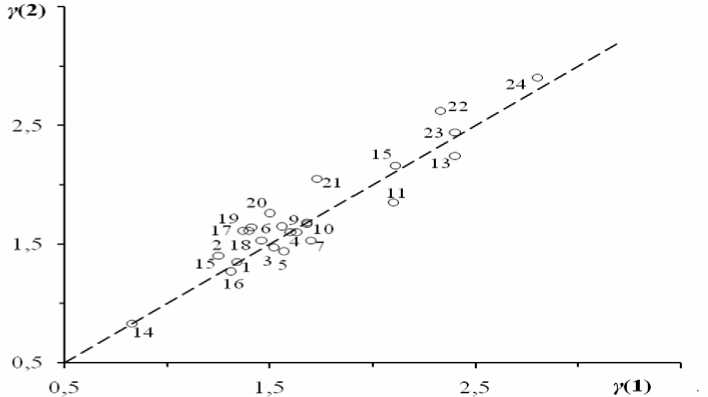
Рис. 1. Сравнение значений параметра Грюнайзена, рассчитанных по уравнению Грюнайзена γ(1) и по формуле

Леонтьева γ(2), для различных кристаллов. Номера точек соответствуют номерам твердых тел в табл. 1

Сравнение уравнений Леонтьева и Грюнайзена для кристаллических твердых тел

В табл. 1 сопоставляются результаты расчета γ по указанным уравнениям. Данные о величинах ρ, В А , v S и v L , входящих в формулу Леонтьева, взяты из обзора [2]. Значения γ по уравнению Грюнайзена (1) были получены ранее [3]. Как видно из табл. 1, для различных кристаллов соотношение Леонтьева удовлетворительно согласуется с уравнением Грюнайзена.

Лучшее согласие наблюдается, на первый взгляд, для квазиизотропных щелочногалоидных кристаллов с центральными силами взаимодействия частиц, что можно было попытаться объяснить тем, что при выводе соотношения Леонтьева была использована теория упругости, которая справедлива для изотропной сплошной среды, а заметные отклонения от согласия между рассматриваемыми уравнениями для ряда твердых тел (рис. 1) считать обусловленными анизотропией этих систем.

Однако скорее всего причина таких отклонений заключается просто в разбросе значений γ, полученных разными исследователями. Так, например, по трем разным источникам параметр Грюнайзена (1) для алюминия составляет 2,11, 2,43 и 2,34 [4].

Таблица 1

Сопоставление результатов расчета параметра Грюнайзена γ по уравнениям Грюнайзена (1) и Леонтьева ( 2) для кристаллических твердых тел (использованы данные [2-4])

№	Элементы и соединения	µ	γ
			Леонтьев (2)	Грюнайзен (1)
1	LiF	0,214	1,35	1,34
2	NaCl	0,243	1,53	1,46
3	LiCl	0,245	1,47	1,52
4	KCl	0,259	1,60	1,60
5	NaF	0,234	1,44	1,57
6	NaBr	0,270	1,65	1,56
7	LiBr	0,256	1,53	1,70
8	KBr	0,283	1,67	1,68
9	Fe	0,292	1,68	1,68
10	KI	0,265	1,6	1,63
11	Co	0,357	1,85	2,10
12	Al	0,340	2,16	2,11

13	Ag	0,379	2,24	2,40
14	Be	0,034	0,83	0,83
15	Y	0,245	1,40	1,25
16	NaNO 3	0,257	1,27	1,31
17	NaClO 3	0,270	1,61	1,37
18	Th	0,254	1,61	1,40
19	Mg	0,270	1,64	1,41
20	RbBr	0,267	1,76	1,50
21	Ta	0,337	2,05	1,73
22	AgBr	0,396	2,62	2,33
23	Pd	0,374	2,44	2,40
24	Au	0,420	2,90	2,80

Расчет по уравнению (1) выполнен Беломестных и Теслевой [3].

Комментарий к выводу формулы Леонтьева . Отмечая удовлетворительное согласие соотношения Леонтьева с уравнением Грюнайзена, вместе с тем необходимо признать, что его вывод не является безупречным. Рассмотрим кратко приближенный вариант вывода данной формулы [1]. Из закона сохранения энергии для адиабатического процесса C v dT = pdV и из определения коэффициента

объемного теплового расширения в = .1 f dV J в V I dT J следует приближенное выражение pv . C^.                                   (4) p e Для давления используется уравнение „ = 2 UL,                                           (5) p 3V где объемная плотность средней энергии теплового движения молекул выражается через среднеквадратичную скорость звука (3)

U

V = pv^

Из последних трех соотношений (4)–(6) вытекает связь тепловых характеристик β и СV со скоро- стями распространения продольной и поперечной звуковых волн

C V в

3 ^Р^

которая находится в согласии с экспериментальными данными [1]. Получение указанной связи явля- ется основной задачей работы Леонтьева [1]. С учетом этого равенства (7) в приближении B ≈ BA (Cp

C V ) уравнение Грюнайзена (1) переходит в формулу Леонтьева

3 f—12 I pvk J

Наряду с приближенным вариантом Леонтьев дает более строгий вывод своей формулы (2). Однако в обоих случаях используется основное уравнение молекулярно-кинетической теории идеального газа (5). В связи с этим возникает вопрос об оправданности применения формулы давления идеального газа к твердым телам. Один из более вероятных ответов на данный вопрос, по-видимому, заключается в том, что Леонтьев под давлением р в выражении (5) подразумевает фононное давление твердых тел, поскольку, во-первых, он выражает его через скорость звука (6) и, во-вторых, нигде в работе [1] не употребляются термины типа «давление идеального газа», «уравнение кинетической теории газа». Формула (5) записывается после предложения: «Затем применим следующее соотношение классической и квантовой физики для связи давления со средней энергией молекулы», причем без ссылок на какие-либо источники.

Однако в этом случае необходимо отметить, что хотя тепловое фононное давление в твердом теле формально совершенно подобно давлению газа (5):

U p- = ^V ’ тем не менее в отличие от (5) в качестве численного коэффициента пропорциональности выступает параметр Грюнайзена γ [5]. Давление фотонного газа (электромагнитной волны) пропорционально плотности энергии, но также с иным численным коэффициентом, чем в (5): p = (1/3)UV [5].

Другой вариант ответа на поставленный выше вопрос основан на представлении Френкеля [6, 7] о возможности применения формулы (5) к твердым телам. По-видимому, он фактически аналогичен первому варианту. Уравнение состояния есть условие баланса, которое требует, чтобы внешнее давление р совместно с внутренним давлением р i уравновешивало тепловое давление p t , действующее на поверхность твердого тела изнутри [5-7]

p + p i = p t

В идеальном газе не возникает надобности различать его внешнее и тепловое давления, ибо p i = 0 и p = p_t , а в твердом теле ситуация противоположная: p <<  p_i ≈ p_t . В балансе огромных противоборствующих давлений p_i ≈ p_t ≈ 10⁴ атм совершенно теряется внешнее атмосферное давление p = 1 атм.

Френкель [6] отмечает, что «тепловое давление, которое оказывает атом, связанный почти упругим образом в твердом теле, на один из боковых атомов, по своей зависимости от температуры очень похоже на то давление, которое он оказывал бы, будучи совершенно свободным, т.е. если бы мы имели дело не с моделью твердого тела, а с моделью газа». Он предлагает расчет коэффициента теплового расширения твердого тела, основанный на применении формулы давления идеального газа (5) и на равенстве величин pt и pi [7]. Причиной теплового расширения по Френкелю с формальной точки зрения является давление p = в $V- • (8)

V

«численно равное тому внешнему давлению (отрицательного знака), которое могло бы вызвать то же самое изменение объема ΔV при T = 0 K, но приложенное к поверхности тела с внутренней ее стороны» [7]. По своей природе это давление р не имеет ничего общего с упругим напряжением, которое им вызывается и уравновешивается. «Будучи непосредственно обусловленным тепловым движением, оно представляет собой не что иное, как равнодействующую сил, испытываемых… внутренними атомами со стороны поверхностных, которые стремятся от них оторваться».

«Если бы взаимная связь атомов внезапно исчезла, то для удержания их в данном объеме V пришлось бы приложить внешнее давление р, которое определяется известной формулой кинетической теории газов»

pV = 2 U •

«Поскольку р, определяемое (9), может на самом деле компенсировать силы межатомного сцепления, оно должно совпадать с введенным выше давлением р» (8) [7].

Таким образом, с этих позиций давление в соотношении (5), по-видимому, можно рассматривать как тепловое давление, которое по величине должно совпадать с давлением в выражении (4), которое имеет смысл внутреннего давления, против которого совершает работу система за счет убыли внутренней энергии при адиабатическом процессе.

Обращает внимание тот факт, что равенство (5) напомина е т первый закон Грюнайзена

( mn ) U                                 (10)

B =

• I    9 J V

(m и n – параметры потенциала Ми), поскольку модуль объемного сжатия не только пропорционален давлению, но для газов совпадает с ним. Интересно заметить, что сравнение (10) с уравнением Леонтьева (2), записанным в виде

_D f 2 y )    ₂    ( 2 у ) U

B , = p v ,² =         —,

A I 3 J^ k I 3 J V приводит к формуле для параметра Грюнайзена при BA ≈ B (Cp ≈ CV) Y = m^ f C^^ ^ m^ , 7     6 ICv J 6

которая в первом приближении находится в согласии с экспериментальными данными, в частности, для ионных кубических кристаллов ( n ≈ 12, m ≈ 1, откуда γ ≈ 2).

В заключении данного раздела подчеркнем два момента. Во-первых, при применении уравнения Леонтьева (2) необходимо иметь в виду, что при его выводе делается не совсем очевидное допущение (5). Во-вторых, на данном этапе (ввиду отсутствия убедительного обоснования указанного допущения) уравнение Леонтьева в принципе можно использовать по крайней мере в качестве эмпирическо- го или полуэмпирического соотношения, которое находится в удовлетворительном согласии с опытными данными [3, 4, 8-10].

Таблица 2

Плотность ρ, скорости распространения продольных ( v_L ) и поперечных ( v_S ) акустических волн, модуль объемного сжатия В_А и параметр Грюнайзена γ для стекол Na₂O – Al₂O₃ – SiO₂ [11]

№ стекла	Состав по синтезу, мол. %			ρ·10-3, кг/м3	ν L , м/с	ν S , м/с	B A ·10-8, Па	µ	γ
	Na 2 O	Al 2 O 3	SiO 2
1	15	0	85	2339	5430	3340	342	0,196	1,28
2	15	5	80	2358	5570	3390	370	0,206	1,31
3	15	10	75	2410	5697	3510	386	0,194	1,26
4	15	15	70	2465	5737	3469	416	0,212	1,34
5	15	20	65	2428	5850	3540	425	0,211	1,34
6	15	25	60	2472	6000	3568	470	0,226	1,40
7	25	0	75	2439	5280	3140	359	0,226	1,40
8	25	5	70	2455	5480	3240	394	0,231	1,41
9	25	10	65	2461	5610	3330	411	0,228	1,40
10	25	20	55	2470	5680	3450	405	0,208	1,32
11	25	25	50	2499	5790	3490	432	0,215	1,35
12	25	30	45	2519	6026	3556	490	0,233	1,43
13	35	0	65	2497	5340	3070	398	0,253	1,52
14	30	5	65	2486	5500	3200	413	0,244	1,47
15	20	15	65	2450	5670	3490	390	0,195	1,28
16	17,5	17,5	65	2447	5746	3458	418	0,216	1,35

Применение формулы Леонтьева к стеклам. По этой формуле нами рассчитан параметр Грюнайзена различных стекол, у которых известны данные о величинах ρ, v_S , v_L и В_А [11-16]. У большинства исследованных стекол полученные значения γ ≈ 1–3 практически совпадают с данными для квазиизотропных ионных кубических кристаллов.

В щелочносиликатных стеклах [11] наблюдается закономерное усиление ангармонизма колебаний решетки с ростом содержания ионов щелочных металлов. Так, например, в стеклах Na 2 O–SiO 2 при содержании Na 2 O: 15, 25 и 35 мол.% значения γ равны 1,28, 1,40 и 1,52. Параметр Грюнайзена кварцевого стекла SiO₂ составляет 1,15. У стеклообразных метафосфатов щелочноземельных металлов RO–P 2 O 5 (R=Mg, Ca, Sr, Ba) [14] при содержании 50 мол.% RO значение γ растет в ряду Mg (γ = 1,2) – Ca (γ = 1,57) – Sr (γ = 1,62) – Ba (γ = 2,1). У стеклообразных халькогенидов As–Se и As–S [15] значения γ сравнительно малы γ = 1,1–1,25. Стеклообразный селен (Se) имеет преимущественно цепочечную структуру. Введение мышьяка приводит к сшиванию части цепей. Поэтому при переходе от Se к стеклу As–Se величина γ падает (с 1,32 до 1,15 у As 2 Se 3 ). У силикатных стекол Na 2 O–Al 2 O 3 – SiO 2 [11], Na 2 O–Li 2 O–SiO 2 [12] и Li 2 O–Al 2 O 3 –SiO 2 [13] значения γ меняются в пределах 1,2–1,5. В качестве примера в табл. 2 приведены значения параметра Грюнайзена для стекол Na 2 O–Al 2 O 3 –SiO 2 . Видно, что величина γ при изменении содержания окислов меняется вполне определенным образом (хотя и в небольших пределах). Например, при росте содержания Al₂O₃ с 0 до 25 мол.% значение γ растет с 1,28 до 1,40 (при 15 мол. % Na 2 O).

Таким образом, расчет параметра Грюнайзена стеклообразных систем по формуле Леонтьева (2) приводит к вполне разумным значениям. Для стекол не так просто найти необходимые экспериментальные данные о величинах, входящих в уравнение Грюнайзена (1), особенно данные о тепловых характеристиках. Поэтому для исследованных систем практически нет возможности сравнить результаты расчета по формуле Леонтьева со значениями γ, следующими из уравнения Грюнайзена. Однако можем сравнить формулу Леонтьева с уравнением Беломестных-Теслевой [3]

з Г i + д ) . (11) у = I I

• 2    ( 2 - 3 д J

Оценка γ по этому соотношению применительно ко многим металлам, ионным и молекулярным кристаллам находится в удовлетворительном согласии с результатами расчета по уравнению Грюнай-зена [3].

На рис. 2 приводится зависимость параметра Грюнайзена γ, рассчитанного по формуле Леонтьева, от функции Беломестных-Теслевой (3/2)(1+µ)/(2–3µ) для натриевоалюмосиликатных стекол с различным содержанием окислов (табл. 2). Видно, что точки ложатся на прямую с тангенсом угла на- клона, равным единице, что указывает на хорошее согласие между уравнениями Леонтьева и Беломе-стных-Теслевой. Такие же результаты получены для других исследованных стекол.

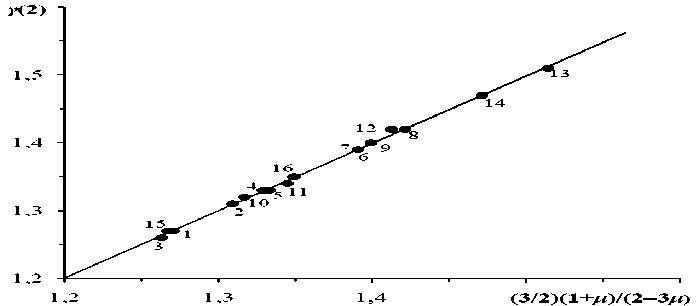
Рис. 2. Сравнение значений параметра Грюнайзена, рассчитанных по уравнению Леонтьева γ(2) и по формуле Беломестных-Теслевой (11), для натриевоалюмосиликатных стекол. Номера точек соответствуют номерам стекол в табл. 2

Если считать оправданным введение для неорганических стекол термодинамического γ D и решеточного γ L параметров Грюнайзена [17-19], то следует считать, что по формуле Леонтьева вычисляется решеточный параметр Грюнайзена γ L ≈ 1,5–3,0. Введение двух параметров Грюнайзена для стекол основано на аналогии с аморфными органическими полимерами, которые характеризуются наличием двух основных типов связей: вдоль полимерной цепи действуют сильные ковалентные связи (– С–С – ), а между цепями более слабые межмолекулярные (вандерваальсовы) связи. Они имеют разные степени ангармонизма. Решеточный параметр Грюнайзена отражает ангармоничность низкочастотных межцепных колебаний, связанных с межмолекулярным взаимодействием, а термодинамический параметр выражает ангармонизм, усредненный по внутрицепным и другим колебательным модам. Расчет по соотношениям, куда входит калориметрическая теплоемкость C_V (в частности, по уравнению Грюнайзена (1)), дает термодинамический параметр Грюнайзена (γ D ≈ 0,5–1), а формулы, куда входят величины, зависящие от межцепного (межмолекулярного) взаимодействия, приводят к решеточному параметру Грюнайзена (γ L ≈ 4–8) [20].

Обычно принято считать, что в щелочносиликатных стеклах имеются две основные системы межатомных связей: более прочные ионно-ковалентные связи Si–O–Si внутри кремнекислородной сетки и сравнительно слабые связи между ионами щелочных металлов (R+), находящихся в пустотах сетки, и немостиковыми «односвязанными» ионами кислорода (Si–O–). Очевидно, что ангармонизм колебаний ионных связей в комплексах Si–(O– R+) выражен значительно сильнее, чем для ионов в кремнекислородной сетке (Si–O–Si). Такая ситуация характерна для фосфатных, боратных, германат-ных и других неорганических стекол. Наличие в стеклах «сильных» и «слабых» связей может быть обусловлено и другими причинами, например, существованием в стеклах трехцентровых мягких связей, мягких конфигураций и т.д. [21].

Поэтому для неорганических стекол по аналогии с полимерами целесообразно ввести два параметра Грюнайзена: решеточный γ _L , характеризующий ангармонизм колебаний «слабых» связей, и термодинамический γ D , выражающий ангармонизм, усредненный по внутрисеточным и другим колебательным модам.

Расчет термодинамического параметра Грюнайзена по уравнению Грюнайзена (1) для ряда неорганических стекол приводит примерно к таким же значениям γ D ≈ 0.5–1.0, что и для аморфных органических полимеров [17-19]. Можно предположить, что и для исследованных в нашей работе стекол термодинамический параметр составляет около γ _D ≈ 0.5–1. Ранее было установлено, что применительно к стеклам уравнение Беломестных-Теслевой приводит к решеточному параметру Грюнайзена [22]. На основе согласия между соотношениями Леонтьева и Беломестных-Теслевой естественно полагать, что по формуле Леонтьева (2) для стеклообразных твердых тел рассчитывается также решеточный параметр Грюнайзена.

Заключение

При выводе формулы Леонтьева (2) используется предположение о том, что для твердых тел применима формула давления идеального газа. Рассмотрены два качественных варианта обоснования этого допущения. Один из них трактует давление, определяемое по формуле кинетической теории газов, как тепловое фононное давление в твердых телах, а другой основан на известных представлениях Френкеля о применении указанной формулы для расчета коэффициента теплового расширения твердых тел. Применение уравнения Леонтьева к стеклам приводит к вполне разумным значениям параметра Грюнайзена.

Выражаем благодарность Беломестных В . Н . за ценные замечания , высказанные при обсуждении данной работы . Работа выполнена при финансовой поддержке гранта БГУ « Лучшая научная школа »