Обоснование процесса гравитационной сепарации зерна методом моделирования

Введение. Современные технологии зерновой продукции нового поколения предъявляют повышенные требования к эффективности процессов сепарирования исходной зерновой смеси. Производят послеуборочное сепарирование (фракционирование) зерна на фуражное и продовольственное; очистку зерна от примесей перед измельчением на мукомольных и комбикормовых заводах и перед шелушением на крупяных заводах [1, 2].

Применяемые в различных отраслях сепараторы для разделения сыпучих материалов отличаются конструктивным многообразием, но большую группу среди них составляют гравитационные сепараторы, разделяющие сыпучие материалы по крупности составляющих их частиц [3–5].

Недостатком известных способов разделения зерновой смеси является снижение производительности за счет возможного зависания зерновых частиц на перфорированных поверхностях предварительной сепарации, выполненных, например, в виде решет. Это также ведет к снижению скорости подачи частиц на сито и к снижению эффективности окончательного просеивания [3].

Поэтому повышение технологической эффективности сепарации зерновых смесей является актуальной задачей для зерноперерабатывающей промышленности.

Анализ последних исследований и публикаций. Для предварительного разгона, сепарации и окончательного просеивания требуется подведение дополнительной энергии. Также известные способы учитывают только скорость витания зерновок и не учитывают такие параметры сепарации, как размеры зерновок и размеры отверстий решет, от которых существенно зависит эффективность сепарации.

В условиях гравитационного поля и применительно к разделяющей поверхности с просеивающими клиновидными отверстиями этим двум требованиям должна удовлетворять криволинейная разделяющая поверхность. Но недостатком неподвижных криволинейных разде- ляющих поверхностей также является забивание просеивающих отверстий [6–8].

Лучшим решением повышения эффективности гравитационной сепарации зернового материала является выполнение разделяющей поверхности сепаратора в форме кривой брахи-стохронного свойства, способной создать оптимальную скорость движения сепарируемых частиц (Василенко П.М., 1960).

Поэтому предлагается для увеличения пропускной способности сепаратора и интенсификации процесса проводить гравитационное сепарирование (фракционирование) с помощью щелевого отверстия, расположенного перпендикулярно направлению движения смеси с шириной, ограничивающейся только габаритами разделяющей поверхности, выполненной в форме кривой брахистохронного свойства [9, 10, 14].

Известно наличие работ математического обоснования оптимальных размеров и формы кривых разделяющих поверхностей, позволяющих частицам или элементам массы двигаться с заданной скоростью [3, 5, 11–13, 15].

Цель представленного исследования заключалась в выполнении математического моделирования и обосновании конструктивных параметров: щелевого отверстия, расположенного перпендикулярно направлению движения смеси с шириной, ограничивающейся только габаритами разделяющей поверхности, выполненной в форме кривой брахистохронного свойства и кинематических параметров движения частиц по разделяющей поверхности для обеспечения эффективной их сепарации.

Материалы и методы исследования. В работе использовались такие общенаучные методы исследования, как методы системного анализа, научных обобщений и математического моделирования.

Результаты исследования и их обсуждение. Предлагаемое нами техническое решение сепарации зерна на разделяющей поверхности с многочисленными просеивающими щелевыми отверстиями имеет принципиальные отличия по сравнению с традиционными кон- струкциями ситовых рабочих органов, в том числе и гравитационных щелевых [9, 10].

Для определения кинематических и геометрических параметров движения цилиндрической частицы (зерна) после её схода с сепарирующей поверхности брахистохронного свойства и условий выделения ее в щелевое отверстие необходимо знать начальную скорость v 0 схода частицы с поверхности кромки сепарирующей поверхности и конечную скорость на расстоянии L между кромками, которые определяют ширину щелевого отверстия. Здесь Н – высота между кромками сепарирующих поверхностей (рисунок 1).

Для выявления события схода частицы на следующую поверхность сепарирующей поверхности или выделения её в щелевое отверстие необходимо знать соотношение начальной скорости частицы v0 в момент схода с поверх- ности кромки сепарирующей поверхности и критической скорости частицы vк.

Для того чтобы частицы цилиндрической формы выделялись в щелевое отверстие сепарирующей поверхности, необходимо выполнение требования v к >v 0 , тогда момент количества движения частицы цилиндрической формы, который определяется v 0 , будет большим, чем момент количества движения частицы, который определяется угловой скоростью вокруг координаты центра масс цилиндра.

Скорость схода частицы с поверхности кромки сепарирующей поверхности при условии, что она поступила на разгонный участок поверхности длиной S0 с нулевой скоростью, определим согласно уравнению v0 = j2 gSo (sinα- f cosα) , (1) где α – угол схода с поверхности кромки сепарирующей поверхности;

ƒ – коэффициент трения скольжения.

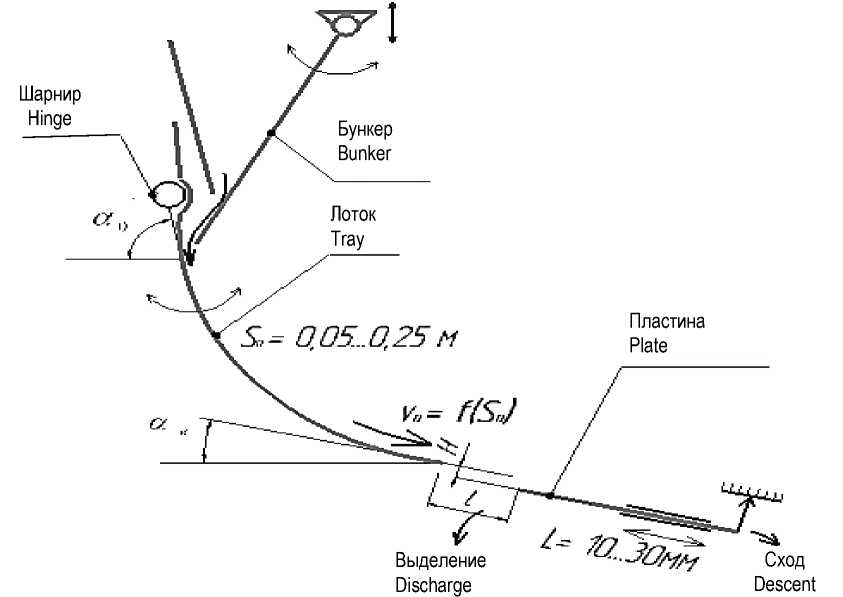
Рисунок 1 – Схема процесса сепарации частиц через щелевое отверстие гравитационного сепаратора Figure 1 – Diagram of the particle separation process through the slit hole of the gravitational separator

Нами рассчитана начальная скорость частицы v0 в момент схода с поверхности кромки сепарирующей поверхности в зависимости от длины разгонного участка сепарирующей поверхности S0 (рисунок 2) и выявлено, что при S0 = 0,15–0,20 м [10] начальная скорость частицы v0 = 0,55–0,72 м/с.

На рисунке 3 показана зависимость критической скорости частицы vк от эквивалентного радиуса re. Для большинства зерновых культур комбикормового производства можно принять re = 2,0–3,0 мм. Тогда критическая скорость частицы цилиндрической формы с таким эквива- лентным радиусом находится в пределах vк = 0,70–0,88 м/с, что больше, чем значения v0 (рисунок 3). Поэтому при таких конструктивных параметрах щелевых отверстий сепарирующей поверхности (рисунок 1) частица заданного размера будет выделена в щелевое отверстие.

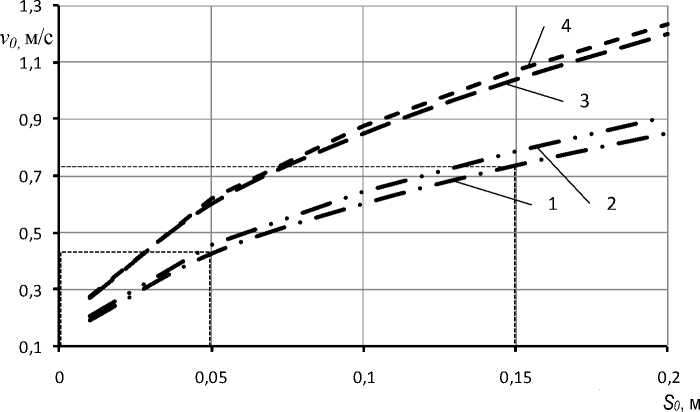
Рисунок 2 – Зависимость начальной скорости частицы v 0 в момент схода с поверхности кромки сепарирующей поверхности от длины разгонного участка сепарирующей поверхности

S 0 : 1 – α = 30°, f = 0,36; 2 – α = 30°, f = 0,33; 3 – α = 40°, f = 0,36; 4 – α = 40°, f = 0,33

Figure 2 – Dependence of the initial velocity of the particle v 0 at the moment of departure from the surface of the edge of the separating surface on the length of the accelerating section of the separating surface

S 0 : 1 – α = 30°, f = 0,36; 2 – α= 30°, f = 0,33; 3 – α = 40°, f = 0,36; 4 – α = 40°, f = 0,33

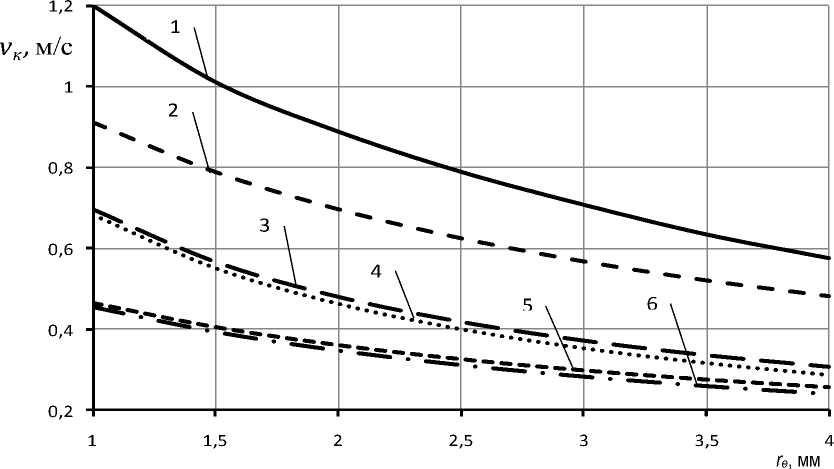
Рисунок 3 – Зависимость критической скорости частицы vк от эквивалентного радиуса re при f = 0,36: 1 – v0 = 0,8 м/с, L = 20 мм, Н = 1 мм; 2 – v0 = 0,8 м/с, L = 20 мм, Н = 2 мм; 3 – v0 = 0,8 м/с, L = 10 мм, Н = 1 мм; 4 – v0 = 0,4 м/с, L = 20 мм, Н = 1 мм; 5 – v0 = 0,8 м/с, L = 10 мм, Н = 2 мм; 6 – v0 = 0,4 м/с, L = 20 мм, Н = 2 мм Figure 3 – Dependence of the critical velocity of the particle vc on the equivalent radius re by f = 0,36: 1 – v0 = 0,8 m/s, L = 20 mm, Н = 1 mm; 2 – v0 = 0,8 m/s, L = 20 mm, Н = 2 mm; 3 – v0 = 0,8 m/s,

L = 10 mm, Н = 1 mm; 4 – v 0 = 0,4 m/s, L = 20 mm, Н = 1 mm; 5 – v 0 = 0,8 m/s, L = 10 mm, Н = 2 mm;

6 – v 0 = 0,4 m/s, L = 20 mm, Н = 2 mm

Анализируя графики зависимостей v 0 и v к (рисунки 2 и 3), приходим к выводу, что они связаны между собой зависимостью v к = k v v 0 . Здесь k v – коэффициент соотношения начальной скорости частицы v 0 в момент схода с поверхности кромки сепарирующей поверхности и критической скорости частицы v к, при которой частица заданного размера будет выделена в щелевое отверстие.

Для того чтобы цилиндрическая частица выделилась в щелевое отверстие, необходимо выполнение условия

J, • to

V„ > —-- c2

.

Из рисунка 4 находим h = l /2 • sin^.(3)

Момент инерции тонкого цилиндра относительно центральной оси равняется:

J = ml2/12.(4)

z _c

Тогда     vc > ±^-.(5)

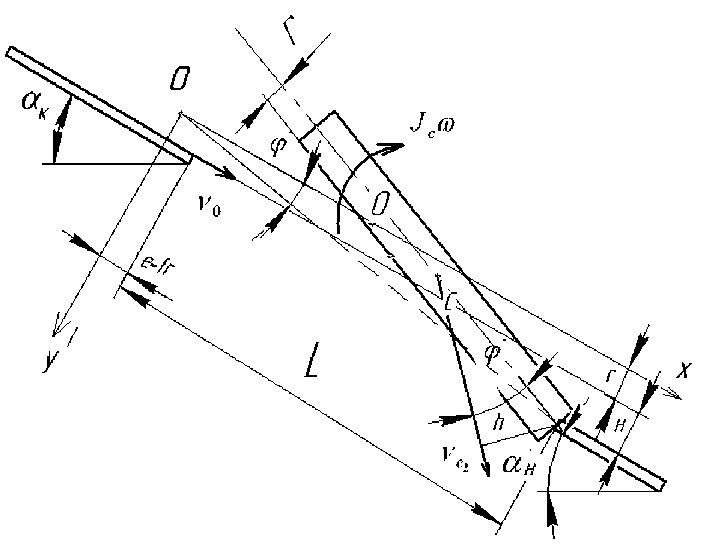
Рисунок 4 – Схема взаимодействия частицы в форме цилиндра с противоположной кромкой щелевого просеивающего отверстия Figure 4 – Diagram of interaction of a particle in the form of a cylinder with the opposite edge of a slit screening hole

Заменяя угловую скорость ω вращения цилиндра вокруг точки соприкосновения его со следующей кромкой сепарирующей поверхности на линейную v_K = to- l , получим:

v vc >--к—

² 6sin ^

.

ω = 10…14°. А для малых углов можно принять Ід ф * sin ^ .

Тогда для выделения цилиндра в щеле- вое отверстие его критическая скорость центра масс при столкновении его со следующей кромкой сепарирующей поверхности должна удовле-

Или

V . >  v ⁰⁰^

² 6sin ^

.

творять условию v > kvV0 (L + fr) . kc    6( H + r )

Из рисунка 4

H + r H + r tg m =      =

L + e L + rf

.

На рисунках 5 и 6 показаны зависимости критической скорости частицы v к от ширины

Для нашего случая при Н =

1–2

мм,

r = 2,5 мм, L = 10–20 мм и f = 0,36, угол поворота цилиндра вокруг центра масс при его движении над щелью до столкновения со следующей кромкой сепарирующей поверхности составит:

щели между противоположными кромками сепарирующих поверхностей L и от разности по высоте между кромками Н сепарирующих поверхностей.

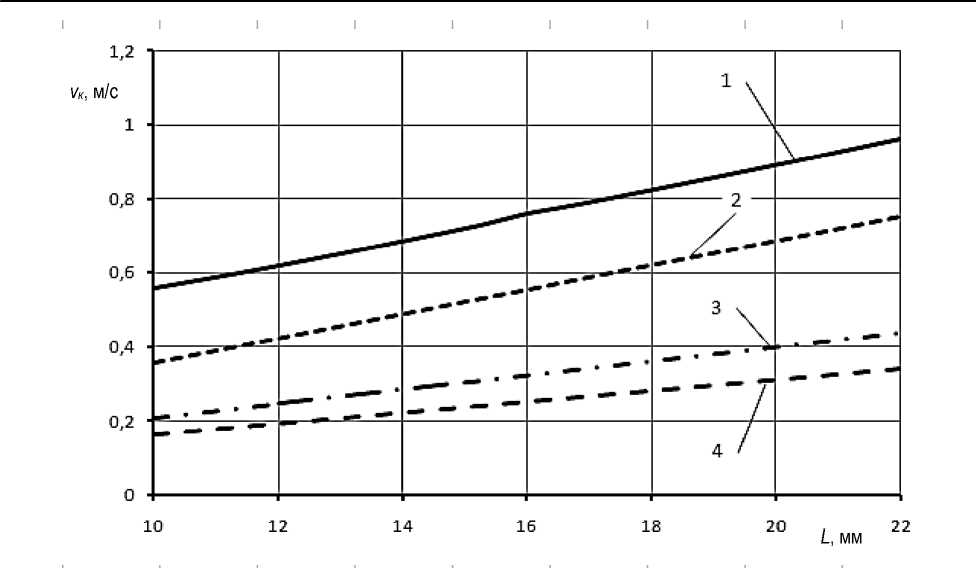
Рисунок 5 – Зависимость критической скорости частицы v к от ширины щели между противоположными кромками сепарирующих поверхностей

L при f = 0,36 и r е = 2,5 мм: 1 – v 0 = 0,8 м/с, Н = 1 мм; 2 – v 0 = 0,8 м/с, Н = 2 мм;

3 – v 0 = 0,4 м/с, Н = 1 мм; 4 – v 0 = 0,4 м/с, Н = 2 мм

Figure 5 – The dependence of the critical velocity of the particle v c on the width of the gap between the opposite edges of the separating surfaces L at f = 0,36 и r е = 2,5 mm: 1 – v 0 = 0,8 m/s, Н = 1 mm;

2 – v 0 = 0,8 m/s, Н = 2 mm; 3 – v 0 = 0,4 m/s, Н = 1 mm; 4 – v 0 = 0,4 m/s, Н = 2 mm

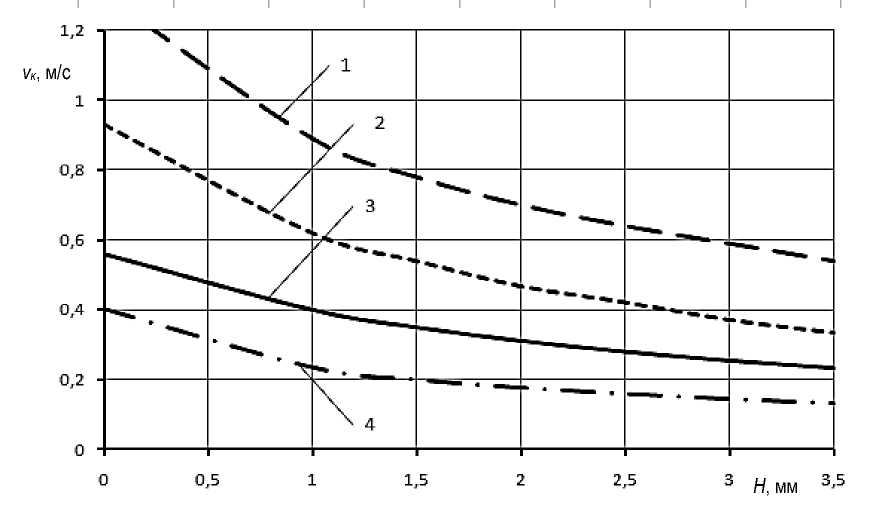
Рисунок 6 – Зависимость критической скорости частицы v к от разности по высоте между кромками Н сепарирующих поверхностей при f = 0,36 и r е = 2,5 мм: 1 – v 0 = 0,8 м/с, L = 20 мм; 2 – v 0 = 0,8 м/с, L = 10 мм; 3 – v 0 = 0,4 м/с, L = 20 мм; 4 – v 0 = 0,4 м/с, L = 10 мм

Figure 6 – Dependence of the critical velocity of the particle v к on the height difference between the edges Н of the separating surfaces at f = 0,36 и r е = 2,5 mm: 1 – v 0 = 0,8 m/s, L = 20 mm; 2 – v 0 = 0,8 m/s, L = 10 mm; 3 – v 0 = 0,4 m/s, L = 20 mm; 4 – v 0 = 0,4 m/s, L = 10 mm

Анализируя графики рисунков 5 и 6, приходим к выводу: чтобы частицы цилиндрической формы с эквивалентным радиусом r e = 2,0– 3,0 мм, которые имеют критическую скорость в пределах v к = 0,70–0,88 м/с, были выделены в щелевое сепарирующее отверстие, необходимо иметь ширину щели между противоположными кромками сепарирующих поверхностей L = 14–20 мм (рисунок 5) и разность по высоте между кромками поверхностей распределительного конуса Н = 1–2 мм (рисунок 6).

При избранных интервалах изменения ширины щели между противоположными кромками сепарирующих поверхностей L = 14–20 мм (рисунок 5), коэффициент соотношения скоростей k v изменяется в интервале 1,03–1,27 при среднем значении 1,15. А при избранных интервалах изменения начальной скорости частицы в момент схода с поверхности кромки сепарирующих поверхностей v 0 = 0,55 – 0,72 м/с (рисунок 2) – k v изменяется в интервале 1,03–1,15 при среднем значении 1,09. Поэтому, для дальнейших расчетов можно принять значение k v в пределах 1,09–1,15.

Выводы. Для выделения частицы с эквивалентным радиусом r e (для большинства зерновых культур комбикормового производства можно принять r e = 2,0 – 3,0 мм) в щелевое отверстие сепарирующих поверхностей при длине разгонного участка S 0 = 0,15 – 0,20 м её начальная скорость должна быть в пределах v 0 = 0,5 – 0,72 м/с, а критическая скорость – в пределах v к = 0,70 – 0,88 м/с, и необходимо иметь ширину щели между противоположными кромками сепарирующих поверхностей в пределах L = 14–20 мм, а разность по высоте между кромками сепарирующих поверхностей Н = 1–2 мм. При этом среднее значение коэффициента k v соотношения начальной скорости частицы v 0 в момент схода с поверхности кромки сепарирующих поверхностей и критической скорости частицы v к , при которой частица заданного размера будет выделена в щелевое сепарирующее отверстие, равно: k v = 1,09 – 1,15.