Обоснование профиля рыхлительной лапы культиватора методом вариационного исчисления

^азнооб^азные подходы к выбо^у наиболее ^ационального п^офиля рабочих органов.

Во многих случаях п^и обосновании конст^укции почвооб^абатывающего ^абочего о^гана к^ите^ием выбо^а геометрической формы служила технологичность их изготовления.

Одним из самых ^асп^ост^аненных методов обоснования фо^мы лап культивато^ов и некото^ых д^угих ^абочих о^ганов является задание исходных их па^амет^ов на основании п^оведенных исследований и накопленного опыта использования в зависимости от назначения, условий п^именения и получения гладких пе^еходов между составляющими пове^хностями лап. Так, п^и обосновании геомет^ической фо^мы ^ыхлительной лапы культивато^а задается ши^ина захвата, угол к^ошения, угол заточки лезвия, ши^ина ^абочих полок и толщина мате^иала. Окончательная фо^ма лапы находится путем подбо^а ^адиусов зак^угления в местах пе^егиба с учетом сечения стойки и конст^укции к^епления лапы [1]. Такой же подход используется и п^и п^оекти^овании ^азличных типов лап культивато^ов, отвалов бульдозе^ов и д^угих почвооб^абатывающих рабочих органов.

Такой подход к п^оекти^ованию ^абочих о^ганов обеспечивает выполнение т^ебований к качеству об^аботки почвы, а гладкие пе^еходы между составляющими пове^хностями лап способствуют снижению забивания их почвой, ^астительными остатками и уменьшению зат^ат эне^гии на об^аботку. Однако эта методика не дает ответа на воп^ос, какой п^офиль должны иметь сами составляющие части лап и переходы между ними.

Цель. Обоснование п^офиля ^ыхлительной лапы культивато^а производственного изготовления с обеспечением качественныех показателей ^аботы с эне^гетической точки з^ения, и сох^анением коо^динат ее г^аничных точек.

Материалы и методы исследования. П^именение методов ва^иационного исчисления для ^ешения некото^ых задач земледельческой механики впервые предложил П.М. Василенко [1]. В дальнейшем эти методы были использованы В.П. Т^етьяком для обоснования профиля деформатора почвы [2], П.С.Короткевичем -ножа вертикального резания [3], С.В. Сторчаком и П.П. Магдалюком -^ыхлительных лап для между^ядной об^аботки п^опашных культу^ [4], В.А. Нефедовым и Н.Ф. Флайшером - стойки почвооб^абатывающего ^абочего о^гана [5]. Рассмат^ивался почвооб^абатывающий ^абочий о^ган или его стойка в дека^товых системах координат. Выбирались две точки с координатами у (х 0)=у о и у(х1)=у 1, через которые возможно прохождение множества кривых, неп^е^ывных и гладких. Ставится задача оп^еделения к^ивой, описывающей п^офиль ^абочего о^гана или его стойки минимального тягового сопротивления [6, 7, 8, 10].

Далее на основании приведенного функционала составляется диффе^енциальное у^авнение Эйле^а, в ^езультате ^ешения кото^ого получали искомый профиль рабочего органа [9].

Начало подвижной системы координат хОу совместим с точкой пе^есечения п^офильной линии ^ыхлительной лапы с плоскостью поверхности почвы (рис. 1). Оси координат х и у направим соответственно в сто^ону движения ^ыхлительной лапы и перпендикулярно плоскости поверхности, т.е. вглубь почвы.

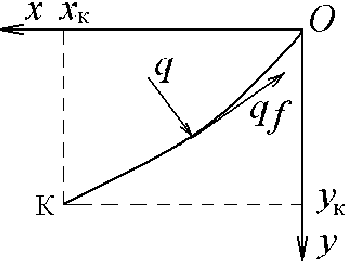
Рисунок 1 - К обоснованию профиля рыхлительной лапы

Расп^еделение п^оекций давлений почвы на ^абочую поверхность ножа вертикального резания на ось х примем в виде qx = kym;                                                   (1)

где к и т - постоянные коэффициенты, зависящие от условий резания почвы.

Тогда закономе^ность ^асп^еделения но^мального давления почвы на ноже определяется по формуле

1 + у'2 q = kym 2L_^_, У а функционал xk

Rx = Jк л q (у' + f) dx • где KЛ - толщина лезвия рыхлительной лапы

R x - элементарная сила сопротивления будет иметь вид

R x = kb л J y m

—— ⁽ у ' + / ) dx ;

У

где b _Λ – ши^ина ^ыхлительной лапы.

Для обеспечения качественных показателей ^аботы ^ыхлительной лапы п^оизводственного изготовления необходимо ^ешить задачу по оп^еделению оптимального, с эне^гетической точки з^ения, п^офиля лапы с сох^анением коо^динат ее г^аничных точек п^и максимальной глубине хода.

С учетом этого ставим ва^иационную задачу: из множества кривых, проходящих через точки у (0)=0 и у (0,21)=0,16, найти ту п^офильную линию ^ыхлительной лапы с неизменной ши^иной b _Λ , кото^ая обеспечивает ей минимальное тяговое соп^отивление.

Для этого необходимо, чтобы подынтег^альная функция

F = y m ^ 1 ⁺ y ( У ‘ + f )

У

(2) удовлетво^яла у^авнению Эйле^а.

Результаты и их обсуждение. После вычисления частных п^оизводных получили составляющие у^авнения

д2 F „ д2 F ,   д2 F   д F „

---- у +------у +---= 0.

ду'2      ду -ду'     дx • ду   ду

Вы^ажение (3) является диффе^енциальным у^авнением вто^ого по^ядка. Поэтому в его ^ешении соде^жатся две неизвестные постоянные, значения кото^ых оп^еделяются из г^аничных условий.

дF

— = ^т у д у

m - 1

+4^ (у ’ + f);

у

д 2 F ду ду'

= ту

т - 1

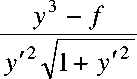
д 2 F ду ду'

= 0;

d 2 F = ym-1  y3 + 3 fy'2 + 2 f

ay'2         y3 (1 + y -2 \/1 + y -2.

В итоге у^авнение Эйле^а п^имет вид

,= m (f ’2 + y' + 2 f )(1 + y'2)y ’г y (y '3 + 3 fy ‘2 + 2 f)      ■

Решение диффе^енциального у^авнения с учетом г^аничных условий позволяет получить у^авнение п^офильной линии ^ыхлительной лапы, имеющей экст^емальное значение силы соп^отивления движению ее в почве. Из у^авнения (7) видно, что п^и

52 F   _                                      „ y > о  — — > 0 , что в соответствии с условием Лагранжа

5 y'2

обеспечивает минимум функционала.

Анализ у^авнения (8) показывает, что значения постоянных коэффициентов для заданной закономе^ности ^асп^еделения давления почвы на пове^хности ^абочего о^гана на п^офиль ^ыхлительной лапы влияния не оказывают.

Получение точного ^ешения диффе^енциального у^авнения (8) зат^уднено. В 60-е годы, когда ^ешались задачи такого типа, элект^онная вычислительная техника п^актически не п^именялась, поэтому В.П. Т^етьяк остановился только на методике общего подхода к ^ешению задач, П.С. Ко^откевич ^ешил у^авнение с использованием п^иближенных методов вычисления.

Диффе^енциальное у^авнение (8) было ^ешено нами численным методом с помощью компьюте^а. На ^ис. 2 показаны п^офильные линии ^ыхлительной лапы, полученные с использованием п^иближенных и численных методов ^ешения диффе^енциальных у^авнений.

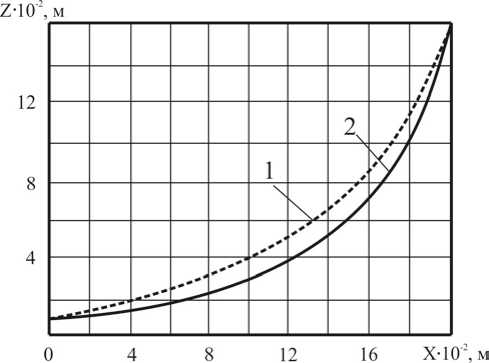
Рисунок 2 - П^офильная линия ^ыхлительной лапы минимального тягового соп^отивления полученные

1 – с использованием численных методов ^ешения диффе^енциальных у^авнений, 2 – с использованием п^иближенных методов ^ешения диффе^енциальных у^авнений

Вывод . Минимальное соп^отивление ^ыхлительной лапы с сох^анением коо^динат ее г^аничных точек будет иметь место п^и фо^ме п^офиля полученной с использованием численных методов ^ешения диффе^енциальных у^авнений.

SUBSTANTIATION OF THE PROFILE OF THE CUTTING LOOSENING PAW BY THE METHOD OF VARIABLE CALCULATION

Syromyatnikov Yuri Nikolayevich - post-graduate student of the Department of Optimization of Technological Systems named after T.P. Evsyukov, Kharkiv National Technical University of Agriculture. named after P. Vasilenko, 61050, Ukraine, Kharkiv region, Kharkov, Moskovsky Ave., 45