Обоснование прогнозов в аграрном производстве и проблемы их актуальной имплементации (на примере Орловской области)
Автор: Шестаков Р.Б., Ловчикова Е.И.
Журнал: Вестник аграрной науки @vestnikogau
Рубрика: Экономические науки
Статья в выпуске: 3 (84), 2020 года.
Бесплатный доступ
В работе авторы обобщают имеющиеся наработки по вопросам методологии агробизнес-форсайта, а конкретно, обоснованию прогнозов сельскохозяйственного производства с использованием методов машинного обучения. Основной целью являлось формирование прогноза на три ближайших года по объемам сельскохозяйственного производства в Орловской области в фактических и сопоставимых ценах. Дополнительно использовались данные производства в целом по Российской Федерации и индексы цен сельхозтоваропроизводителей. В работе применялись «классические» методы моделирования временных последовательностей: OLS, ETS, ARIMA, их производные и комбинации. Более сложные алгоритмы, основанные на баггинге, бустинге или же глубоком обучении не принимались в расчет, так как на исходных данных не дали бы значимого прироста в точности предсказания. Также основным был анализ одномерных данных, с эксклюзивным включением дополнительного измерения в отдельные модели. Подробно показан алгоритм действий, применяемый в процессе машинного обучения. Подбор оптимальной модели производился на обучающей выборке, а валидация моделей - с помощью функции потерь RMSE (корня среднеквадратичной ошибки), на тестовой выборке. Первым шагом на обучающей выборке подбирались параметры для основного ряда. Вторым и третьим шагом вспомогательные модели для двумерных методов первого шага. По итогам был рассчитан краткосрочный трехлетний прогноз в фактических и сопоставимых ценах, определены границы доверительных интервалов. С учетом комплекса кризисных явлений 2020 года обсуждены проблемы выбора сценария возможного движения динамики производства. В условиях усиливающийся неопределенности, принятие решений в процессе управления должно базироваться на соответствующей методологической основе.
Прогнозирование, сельское хозяйство, объемы производства, индекс цен производителей, фактические цены, сопоставимые цены, машинное обучение
Короткий адрес: https://sciup.org/147228857
IDR: 147228857 | УДК: 338.12.017:631.1(470.319) | DOI: 10.17238/issn2587-666X.2020.3.159
Текст научной статьи Обоснование прогнозов в аграрном производстве и проблемы их актуальной имплементации (на примере Орловской области)
Введение. Современные цифровые технологии неуклонно проникают в агробизнес, начиная от биоинформатики, прогнозов урожайности и заканчивая созданием полноценной смарт-фермы со всеми соответствующими технологиями. Процесс управления и форсайта в агробизнесе уже не мыслим без применения современных методов (рис. 1). Машинное обучение (англ. machine learning, ML) – класс методов искусственного интеллекта, характерной чертой которых является не прямое решение задачи, а обучение в процессе применения решений множества сходных задач.
Постановка проблемы, анализ
Тренировка ML
имеющихся данных
алгоритма

Решение
Углубленное
понимание, и если необходимо цикл повторяется

Экспертиза
Рисунок 1 – Машинное обучение в исследованиях [1]
Факторов, влияющих на активность в той или иной отрасли, достаточно много [3, с. 711] и в зависимости от целей исследования, необходимо выбирать тот или иной уровень абстракции. Относительно агробизнеса наиболее значимыми являются сама динамика производства, институциональные, инвестиционные и инновационные параметры [4, c. 67-73; 5, c. 911-923]. В данной работе мы будем использовать региональные и национальные объемы сельскохозяйственного производства, индексы цен производителей продукции сельского хозяйства.
Целью исследований является обоснование прогнозов сельскохозяйственного производства с использованием элементов машинного обучения и пути их дальнейшего использования. Для это прежде всего, были подготовлены данные, проведен разведочный анализ (EDA). Далее определены последовательные шаги в обучении и валидации моделей временных рядов в зависимости от их природы. И, наконец, проведена имплементация прогнозов соотносительно актуальной внешней среде, в которой функционируют предприятия и публичные институты управления.
Условия, материалы и методы. В таблице 1 приведены данные по выпуску и уровню цен производителей в сельском хозяйстве (ИЦП). Для расчета показателей в приведенных ценах, фактические соотнесены с кумулятивными индексами.
Таблица 1 – Продукция сельского хозяйства в Российской Федерации и Орловской области за 1998-2019 гг. [2]
|
Год |
Ежегодный ИЦП, % |
Кумулятивный ИЦП, кол-во раз |
Продукция в приведенных ценах, млрд. руб. |
|
|
РФ |
Орловская область |
|||
|
1998 |
141,9 |
1,4 |
298,4 |
3,2 |
|
1999 |
191,4 |
2,7 |
586,0 |
7,4 |
|
2000 |
122,2 |
3,3 |
742,4 |
9,0 |
|
2001 |
117,5 |
3,9 |
918,2 |
10,6 |
|
2002 |
98,1 |
3,8 |
968,2 |
11,2 |
|
2003 |
124,7 |
4,8 |
1076,4 |
12,0 |
|
2004 |
117,7 |
5,6 |
1253,2 |
14,1 |
|
2005 |
103,0 |
5,8 |
1380,9 |
14,7 |
|
2006 |
110,4 |
6,4 |
1570,6 |
14,7 |
|
2007 |
130,2 |
8,3 |
1861,0 |
19,3 |
|
2008 |
102,5 |
8,5 |
2354,5 |
25,0 |
|
2009 |
98,2 |
8,4 |
2390,1 |
24,7 |
|
2010 |
123,6 |
10,3 |
2462,2 |
27,3 |
|
2011 |
94,9 |
9,8 |
3098,7 |
36,6 |
|
2012 |
110,8 |
10,9 |
3160,3 |
39,1 |
|
2013 |
102,7 |
11,2 |
3458,3 |
43,0 |
|
2014 |
114,1 |
12,7 |
4031,1 |
45,3 |
|
2015 |
108,5 |
13,8 |
4794,6 |
62,0 |
|
2016 |
101,8 |
14,1 |
5112,3 |
69,0 |
|
2017 |
92,2 |
13,0 |
5109,5 |
61,0 |
|
2018 |
112,9 |
14,6 |
5348,8 |
72,3 |
|
2019 |
95,5 |
14,0 |
5907,9 |
93,2 |
Примечание. Рассчитано авторами по данным ФСГС РФ [2].
В таблице 2 рассчитаны базовые показатели описательной статистики исследуемых данных. Надо отметить также наличие значимой коинтеграции между динамикой сельхозпроизводства в Орловской области и в целом по России (тест Энгла-Грэнджера).
Таблица 2 – Разведочный анализ динамических рядов
|
Статистики |
Накопленный (кумулятивный) PPI, кол-во раз |
Продукция в сопоставимых ценах, млрд. руб. |
Продукция в сопоставимых ценах, млрд. руб. |
|
Минимум |
1,4 |
298,4 |
3,2 |
|
Максимум |
14,6 |
5907,9 |
93,2 |
|
Размах |
13,2 |
5609,5 |
90,0 |
|
Медиана |
8,5 |
2372,3 |
24,85 |
|
Среднее хронологическое |
8,6 |
2608,6 |
31,7 |
|
Волатильность среднегодовая |
0,9 |
374,8 |
5,4 |
|
Дрифт в абсолютном выражении |
12,6 |
5609,5 |
90 |
|
Дрифт (кол-во раз) |
9 |
19 |
28 |
Примечание. Рассчитано авторами по данным таблицы 1.
В качестве калибровочных моделей (нулевая модель, бенчмарк) будем использовать дрифт ряда, где предсказанные значения есть экстраполяция дрифта или, другими словами, линии роста от первого до последнего значения ряда.
В качестве основных моделей предполагается:
-
1) линейный тренд;
-
2) сглаживание ETS;
-
3) ARIMA;
-
4) динамическую регрессию с экзогенными переменными и ARIMA-ошибками;
-
5) ансамбли вышеуказанных моделей с наилучшими средними метриками.
С помощью программной среды анализа данных «R» были подобраны следующие параметры в сетевом режиме [6, 7]. В процессе обучения моделей отбор осуществлялся по скорректированному для малых выборок информационному критерию Акаике – AICс. Ряды разделены на обучаемую (1998-2016 гг.) и тестовую выборку для валидации (2017-2019 гг.). Сопоставление проводилось по функции потерь RSME (root mean squared error – квадратный корень среднего квадрата отклонения), которая позволяет сравнивать данные в различных единицах измерения или шкалах. RSMЕ более чувствителен к выбросам, чем МАЕ (mean absolute error, средняя абсолютная ошибка). Метрика представлена в тех же единицах, что и исходные данные.
Результаты и обсуждение. Рассчитаем необходимые параметры в несколько этапов (табл. 3-5) и сведем окончательные результаты (табл. 6).
Таблица 3 – Шаг 1. Сопоставление обученных моделей на тестовой выборке по метрике RMSE (Орловская область)
|
Модели |
Гиперпараметры (заданные параметры) |
Параметры (полученные параметры) |
Статистическая значимость Модели / коэффициентов (+), (-) |
RMSE |
|
Тестовая выборка (реальные значения): Y 2017 = 4,7; Y 2018 = 4,9; Y 2019 = 6,7 |
||||
|
Нулевые модели |
||||
|
Последнее значение |
Y 2017-2019 = Y 2016 |
Y 2017-2019 = 4,9 |
+ |
14,8 |
|
Дрифт |
d = 3,7 Y t = Y 1 + dt |
Y 2017 = 72,7 Y 2018 = 76,3 Y 2019 = 80,0 |
+ |
13,0 |
|
Основные модели |
||||
|
Линейный тренд |
Наличие свободного члена Y = const + kt |
k = 3,1 const = -5,6 (R2= 0,88) |
+/ k+ const -* |
18,7 |
|
ARIMA |
(0,2,1) |
ma 1 =-0,72 (AICc=101,7) |
+/+ |
10,9 |
|
Динамическая регрессия с ошибками ARIMA |
Без свободного члена Экзогенные переменные: Производство РФ ИПЦ Модель ARIMA-ошибок: (0,0,0) |
k рф = 0,02 k ицп = -0,68 const = -5,6 (AICc=84.69) |
+/+ |
8,9 |
|
ETS |
(М, A, N) |
alpha = 1 beta = 0.3 gamma = 0 |
+/+ |
10,9 |
|
Оптимизированный мульти модельный ансамбль |
Модели 5+6 |
8,2 |
||
Примечание. Рассчитано авторами. *Несмотря на то, что свободный член в модели статистически не значим, в целом модель показала лучшую метрику, чем на аналоге без свободного члена вообще.
Основные модели, кроме линейного тренда, в достаточной степени опережают по точности бенчмарк. Оптимизированный мультимодельный ансамбль находится как наилучшая комбинация моделей, чье среднее значение имеет наименьший скоринг RMSE. В нашем случае оптимальный ансамбль также превзошёл показатели отдельных, входящих в него моделей.
Выбранные модели будем использовать для экстраполяции на 2020-2022 гг. Дополнительную сложность вносит динамическая регрессия, так как для ее прогноза требуется помимо прочего экстраполяция экзогенных переменных (сельхозпродукция по России и индекс цен производителя). Необходимо повторить отбор моделей по частичной аналогии (табл. 4 и 5).
Таблица 4 – Шаг 2. Сопоставление обученных моделей по тестовой выборке для производства по Российской Федерации
|
Модели |
Гиперпараметры (заданные параметры) |
Параметры (возвращенные параметры) |
Статистическая значимость модели / коэффициентов (+), (-) p<0,05 |
RMSE |
|
Тестовая выборка (реальные значения): Y 2017 = 5109,5; Y 2018 = 5348,8; Y 2019 = 5907,9 |
||||
|
Нулевые модели |
||||
|
Последнее значение |
Y 2017-2019 = Y 2016 |
Y 2017-2019 = 5112,3 |
+ |
479,2 |
|
Дрифт |
d = 267,4 Y t = Y 1 + dT |
Y 2017 = 5379,7 Y 2017 = 5647,2 Y 2017 = 5914,6 |
+ |
232,5 |
|
Основные модели |
||||
|
Линейный тренд |
Наличие свободного члена Y = const + kt |
k = 246.90 const = -283.90 (R2= 0,94) |
+/+ |
573,1 |
|
ARIMA |
(0,2,1) |
ma 1 =-0.75 (AICc= 236,8) |
+/+ |
482,3 |
|
ETS |
(М, A, N) |
alpha = 1,00 beta = 0,24 gamma = 0 (AICc = 260,3) |
+/+ |
473,2 |
|
Оптимизированный ансамбль |
Средний прогноз моделей 2+5 |
- |
- |
341,8 |
Таблица 5 – Шаг 3. Сопоставление обученных моделей по тестовой выборке (по метрике RMSE (для индекса цен производителя)
|
Модели |
Гиперпараметры (заданные параметры) |
Параметры (возвращенные параметры) |
Статистическая значимость модели в целом / коэффициентов (+), (-) |
RMSE |
|
Тестовая выборка (реальные значения): Y 2017 = 13,0; Y 2018 = 14,6; Y 2019 = 14,0 |
||||
|
Нулевые модели |
||||
|
Последнее значение |
Y 2017-2019 = Y 2016 |
Y 2017-2019 = 14,1 |
+ |
0,7 |
|
Дрифт |
d = 0,7 Y t = Y 1 + dT |
Y 2017 = 14,8 Y 2017 = 15,5 Y 2017 = 16,2 |
+ |
1,7 |
|
Основные модели |
||||
|
Линейный тренд |
Наличие свободного члена Y = const + kt |
k = 0,83 const = 0,68 (R2= 0,99) |
+/+ |
1,4 |
|
ARIMA |
(1,1,0) + drift |
ar 1 =-0,46 drift = 0,7 (AICc=30,32) |
+/+ |
1,9 |
|
ETS |
(A, A, N) |
alpha = 0,76 beta = 0,76 gamma = 0 (AICc = 42,8) |
+/+ |
1,7 |
В таблице 6 собраны точечные прогнозы и доверительные интервалы прогноза (ДИП).
Таблица 6 – Прогнозные данные в соответствии с выбранными моделями временных рядов на 2020-2022 гг. (Орловская область, млрд. руб.)
|
Годы |
Нижний 95% ДИП |
Нижний 80% ДИП |
Точечное значение |
Верхний 80% ДИП |
Верхний 95% ДИП |
|
ETS |
|||||
|
2020 |
69,3 |
79,8 |
99,7 |
119,6 |
130,2 |
|
2021 |
58,7 |
75,2 |
106,3 |
137,3 |
153,8 |
|
2022 |
48,9 |
71,0 |
112,8 |
154,6 |
176,7 |
|
Динамическая |
регрессия |
||||
|
2020 |
81,7 |
84,2 |
88,7 |
93,3 |
95,7 |
|
2021 |
86,9 |
89,3 |
93,9 |
98,5 |
100,9 |
|
2022 |
92,1 |
94,5 |
99,1 |
103,7 |
106,1 |
|
Ансамбль моделей |
|||||
|
2020 |
75,5 |
82,0 |
94,2 |
106,5 |
112,9 |
|
2021 |
72,8 |
82,3 |
100,1 |
117,9 |
127,3 |
|
2022 |
70,5 |
82,8 |
106,0 |
129,1 |
141,4 |
|
Ансамбль моделей в сопостави мых ценах (c учетом накопленного индекса цен 14,1) |
|||||
|
2020 |
5,4 |
5,8 |
6,7 |
7,6 |
8,0 |
|
2021 |
5,2 |
5,8 |
7,1 |
8,4 |
9,0 |
|
2022 |
5,0 |
5,9 |
7,5 |
9,2 |
10,0 |
Примечание. Рассчитано авторами.
На рисунках 2 и 3 изображены графики динамических рядов производства сельскохозяйственной продукции в Орловской области в текущих и сопоставимых ценах.
Нижний 95% ДИ ^^^^Нижний 80% ДИ ^^^™Точечный прогноз
Верхний 80% ДИ ^^^м Верхний 95% ДИ
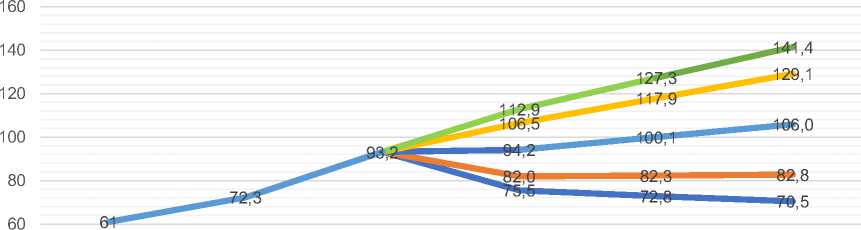
2017 2018 2019 2020 2021 2022
Рисунок 2 – Краткосрочный прогноз по динамическому ряду сельскохозяйственного производства в Орловской области (в текущих ценах), млрд руб.1
3Нижний 95% ДИ ^^^мНижний 80% ДИ ^^^^Точечный прогноз
Верхний 80% ДИ ^^^мВерхний 95% ДИ 11,0 10,0 9,0 8,0 7,0 6,0 5,0 4,0 3,0 2017 2018 2019 2020 2021 2022
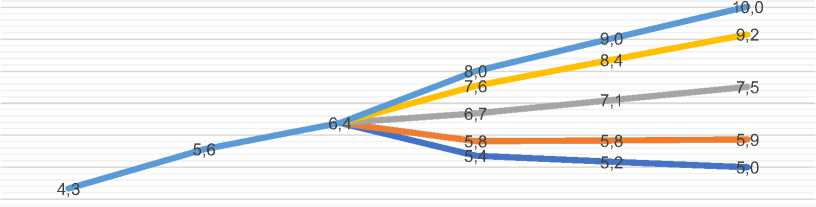
Рисунок 3 – Краткосрочный прогноз по динамическому ряду сельскохозяйственного производства в Орловской области (в сопоставимых ценах), млрд руб.2
В результате можно заметить достаточно определенный разброс, где положительный сценарий превалирует над отрицательным по потенциалу роста. Сравним разницу 2,5 млрд. руб. в случае крайне положительной динамики, и 1,5 – в обратном движении от точечных значений. Однако, уже в 2020 году мы стали свидетелями прибытия практически «стаи черных лебедей»: COVID-19 и падения ресурсных рынков. Экспертами уже оцениваются потери мировых рынков более 6 трлн долл. [8], что естественно скажется на российской экономике. Нет никаких сомнений, что при планировании в подобном случае в расчет придется брать наиболее негативное развитие событий. Помимо этого, усиление неопределенности потребует более глубинных подходов в обосновании прогнозов, расширения круга изучаемых факторов и используемых инструментов.
Выводы. 1. Динамика сельскохозяйственного производства хорошо поддается прогнозированию на исходных данных в процессе машинного обучения с использованием классических методов.
-
2. Доверительные границы прогноза в целом показывают смещение в позитивную зону.
-
3. Рост неопределенности в российской и экономике в 2020 году приводит к имплементации негативных сценариев при планировании и принятии решений.
-
4. Необходимо усложнить прогностический алгоритм для более глубокого анализа развития ситуации.
Список литературы Обоснование прогнозов в аграрном производстве и проблемы их актуальной имплементации (на примере Орловской области)
- Geron A. Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems. O'Reily Media, Inc. 2017.
- Официальная статистика. Предпринимательство. Сельское хозяйство, охота и лесное хозяйство. Продукция сельского хозяйства // URL: http://www.gks.ru (дата обращения: 12.04.2020).
- Выявление особенностей стратегического развития регионов на основе статистического анализа индикаторов / Д.А. Масленников, С.Н. Митяков, Л.Ю. Катаева, Т.А. Федосеева // Экономика региона. 2019. Т. 15, вып. 3. С. 707-719.
- Шестаков Р.Б., Ловчикова Е.И Анализ динамики аграрного производства в условиях общей экономической рестрикции // Экономика, труд, управление в сельском хозяйстве. 2017. № 4 (33). С. 65-73.
- Шестаков Р.Б., Ловчикова Е.И. Инвестиционный акселератор сельскохозяйственного производства // Экономика региона. 2019. Т. 15, вып. 3. С. 908-923. DOI: 10.17059/2019-3-21
- Hyndman R.J. A forecast ensemble benchmarks // URL: https://robjhyndman.com/hyndsight/benchmark-combination/ (дата обращения: 22.02.2020).
- Package "forecast" // URL: https://cran.r-project.org/web/packages/forecast/forecast.pdf (дата обращения: 12.04.2020).
- The World Bank // URL: https://www.worldbank.org (дата обращения: 30.03.2020).


