Обоснование типового капельного орошения томатов на Губа-Хачмазском массиве

Бюллетень науки и практики / Bulletin of Science and Practice

Исследования проводилось в фермерском хозяйстве Шабранского района. Опытный участок состоял из 0,4 га плантаций томатов, который орошался бороздами и капельным орошением.

Типизация выбранных экспериментальных полей для массива оценивается на основе гипотезы о случайной зависимости коэффициентов соответствия и координат. Задача типизации в данном случае, это определение количественных измерений подобия областей и массивов, характеризующихся рядом признаков, суть методики которой поясняется ниже.

Природные условия Губа-Хачмазского массива характеризуются множеством факторов и особенностей. Поскольку одни из этих факторов играет основную роль в процессе, его следует рассматривать как первичный, а другие — как относительно незначительные. Используется интеллектуальная концептуальная модель, основанная на «теории вероятности» [1, 3].

Математически эта проблема выражается по следующей форме: вероятность того, что случайный (m) — мерный (vm) вектор, пространственно (m) — мерное (S m ) поле принадлежит пространству, и символически выражается следующей формулой:

P • ( W m C S m ) = J S m ... J ^ • ⁽ a i ^-a ₂ .. ^ n ) • d m ... d p_i0 n                        ⁽¹⁾

Эта зависимость дает начальное представление о характере и типе информации, необходимой для решения проблемы. Для изучения в первую очередь следует выбрать показатели, определяющие их типичность.

После выбора индикатора необходимо полностью изучить факторы в области их относительной типичности. Показатели бывают не одноименными и следовательно, их математическое обозначение не только является смешанным, но и должно подчиняться закону распределения соответствующей вероятности. Таким образом, необходимо определить тип закона распределения показателей первичной эмиссии.

mm

P = П Ч1 " П ^ " Pka ) ]}

где: m — количество символов; k — количество знаков первой степени; — символ умножения; а — количество второстепенных признаков; P k , a — вероятность совпадения одноименных знаков. Вероятность появления одноименных признаков рассчитывается следующим образом:

P a =Ф * (

S • —a       S • —a

—----) -Ф ( — i ----)

Ta

Ta

где: а — нижняя и верхняя границы эталонного диапазона характеристик в области практики; S — средний квадрат наклона знаков зоны; a — математическое ожидание знаков зоны; ^T _a интеграл вероятностей (функция Лапласа).

Из выражений 2 и 3 видно, что для расчета P k , a необходимо знать закон распределения случайных величин характеристик экспериментального участка и зоны. После того, как станет известна регулярность распределения случайных величин, составляется блок-схема расчетной модели усреднения. В схеме символы первого порядка расположены на последовательной прямой, а символы второго порядка — на параллельных линиях [2] (Рисунок).

Исходя из этого, для расчета P k , a по закону распределения знаков и статическим характеристикам величин a и T _a нижнюю и верхнюю границы эталонного диапазона знаков в поле эксперимента (S i , S i ,) требуется установить. Нижний и верхний пределы диапазона можно определить по следующей формуле:

S/ = a- — 3 • т и S• = a. + 3 • т .

i           i                a i           i            i               a i

Основными характеристиками блок-схемы являются скорость проникновения воды в почву, гранулометрический состав почвы, испарение и количество атмосферных осадков; В качестве второстепенных характеристик были приняты пористость почвы, плотность твердой фазы, плотность скелета почвы и минимальная влажность. Информация о выбранных функциях представлена в Таблице 1, разработана соответствующая блок-схема (Рисунок).

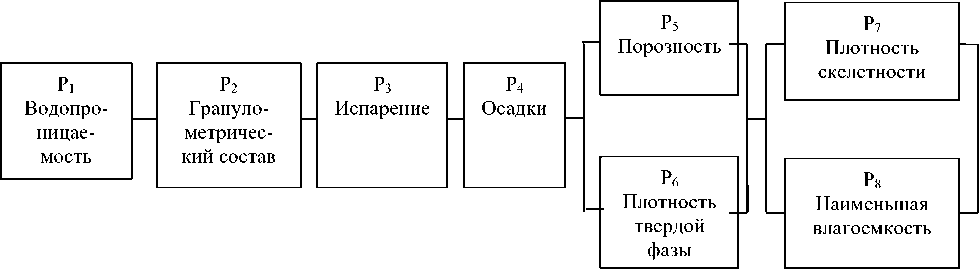
Рисунок 1. Блок-схема размещения особенностей типичности объекта исследований по Губа-Хачмазскому массиву

Данные были проанализированы в соответствии с существующей методологией, и рассматриваемая модель была рассчитана по следующей формуле:

P = P 1 × P 2 × P 3 × P 4 × [1-(1-P 5 ) × (1-P 6 ) × (1-P 7 ) × (1-P 8 )]

где: P 1 — скорость водопоглощения, мм/мин; P 2 — гранулометрический состав, <0,01 мм %; P 3 — испарение, мм; P 4 — количество осадков, мм; P 5 — пористость грунта, %; расчеты проводились с использованием данных Таблицы.

P = P 1 X P 2 X P 3 x P 4 X [ 1-(1-P 5 ) X (1-P 6 ) X (1-P₇) X (1-P₈) ] = Q,99xQ,95xQ,95xQ,91x [ 1-(1-0,90) x (1-0,85) x (1-0,84) x (1-0,65) ] = 0,8QxQ,99 = 0,792 = 79,2%.

Таблица

СРАВНИТЕЛЬНЫЙ АНАЛИЗ ПОКАЗАТЕЛЕЙ ПОЧВЫ ГУБА-ХАЧМАЗСКОГО МАССИВА

^	Признаки	§ 3 Q s s s	Объект исследования			Губа-Хачмазский массив	s 13 § 5 S Ф
			0 s $	* § О* 0	'S s	Диапазон эталона
P 1	Скорость водопроницаемости	мм/мин.	1,17	0,48	4	1,76–2,07	0,99
P 2	Гранулометрический состав	< 0,01 мм %	38,2	2,39	6	24,04–65,56	0,95
P 3	Испарение	мм	800	81,65	3	980–1200	0,95
P 4	Кол-во осадков	мм	363	56,18	4	200–220	0,91
P 5	Порозность почв	%	48,0	8,30	6	39,5–49,5	0,90
P 6	Плотность твердой фазы почв	г/см3	2,70	0,07	3	2,60–2,70	0,85
P 7	Плотность скелетности почв	г/см3	1,41	0,08	3	1,38–1,55	0,84
P 8	Минимальная влагоемкость	%	19,8	1,06	4	20,30–29,10	0,65

Вероятность идентификации для Губа-Хачмазского района по 8 признакам в исследуемом районе Шабранского района P = 0,792 или 79,2%.

По результатам расчета полученная цена может быть признана удовлетворительной для региона и гарантирует, что район исследований типичен для Губа-Хачмазской зоны.