Обоснование требований к цифровым синтезаторам сигналов для различных типов РЛС

Цитирование: Викторов, Д.С. Обоснование требований к цифровым синтезаторам сигналов для различных типов РЛС / Д.С. Викторов, Е.В. Пластинина, Е.В. Самоволина // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(7). С. 818–828. DOI: 10.17516/1999-494X-0268

В [3–10] показано, что квантование фазы и напряжения, дискретизация и интерполяция сигналов в цифровых синтезаторах приводят к появлению модуляционных и внутриполосных искажений спектров формируемых сигналов с угловой модуляцией (УМ) и, следовательно, их корреляционных функций (уменьшения амплитуды, временного смещения и расширения основного лепестка, росту боковых лепестков сжатого импульса). В конечном счете это приводит к снижению потенциальных тактико-технических характеристик (ТТХ) РЛС и является основным фактором, ограничивающим использование в них цифровых синтезаторов сигналов (ЦСС).

Поэтому разработка требований, предъявляемых к ЦСС, для различных типов РЛС является актуальной задачей.

Требования к уровню искажений в РЛС с импульсным и квазинепрерывным излучениями

В РЛС с корреляционно-фильтровым методом обработки радиолокационных сигналов с УМ можно выделить четыре основных источника искажений ( I = 4): ЦСС сигналов с УМ, усилитель мощности передающего канала, усилительный тракт приемного канала и гетеродин [11, 12]. Указанные устройства имеют независимое конструктивное исполнение, поэтому обусловленные ими искажения в первом приближении можно считать некоррелированными, а их вклады в суммарные искажения сигналов на выходе схем обработки примерно одинаковыми. Тогда суммарная спектральная плотность мощности шумов, приведенных к входу приемного устройства, от I некоррелированных источников искажений равна

I

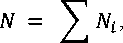
i = 1

где N_i – спектральная плотность мощности i -го источника шума.

В этом случае допустимая спектральная плотность мощности искажений в ЦСС с УМ не должна превышать N Ц _С<  N¹I.

Искажения, возникающие при формировании сигналов с УМ в цифровых синтезаторах, в свою очередь, можно разделить на регулярные и случайные. Регулярные искажения возникают при квантовании и дискретизации формируемого в цифровом синтезаторе сигнала. Эти искажения для каждого вида формируемого сигнала с УМ повторяются от импульса к импульсу. Случайные искажения обусловлены мультипликативным (модуляционным) и аддитивным воздействиями шумов и нестабильностей источников эталонов, источников питания, электронных приборов и т.д. [13, 14]. В первом приближении можно считать, что спектральная плотность мощности регулярных N _Р и случайных N _С искажений имеет равномерный уровень в полосе рабочего диапазона ЦСС и равна между собой. Тогда,

N цс <  N р + N с = 2 N р .

С учетом сказанного выше, допустимая спектральная плотность мощности регулярных искажений в ЦСС с УМ не должна превышать

N р <  N /(2 I) .                                                                     (1)

На практике при предъявлении требований к суммарному уровню указанных искажений исходят из допустимого ухудшения основных ТТХ РЛС. Для большинства классов РЛС одним из важнейших исходных критериев является допустимое снижение вероятности правильного обнаружения по сравнению с ее потенциальным значением A P D = P D - P D ' при фиксированной вероятности ложной тревоги P F [15].

Для обоснования требований к допустимому уровню искажений сигналов с УМ, формируемых ЦСС, применительно к импульсным РЛС рассмотрим случай обнаружения сигнала X [ ( t ), отраженного от малоразмерной цели 1, на фоне шумов n ( t ) и искажений 5 X ₂( t ) сигнала X ₂( t ), от- – 820 –

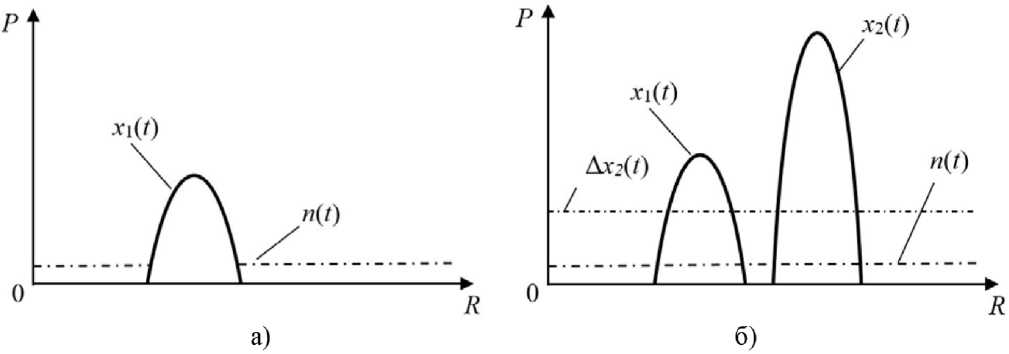
Рис. 1

Fig. 1

раженного от близко расположенной к цели 1 крупноразмерной цели 2 (рис. 1). При отсутствии цели 2 (рис. 1а) параметр обнаружения цели 1 определяется значением

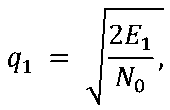
где: Е 1 — энергия сигнала, отраженного от цели 1; N 0 — спектральная плотность мощности шума n (t ).

При наличии цели 2 (рис. 1б) параметр обнаружения цели 1 на фоне шумов n(t ) и искажений 5 X 2 ( ) определяется значением

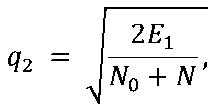
где N — спектральная плотность мощности суммарных искажений в X ₂( t ) сигнала X2(1 ).

Тогда спектральную плотность мощности можно определить в виде

Ai = 2

2      2

<71 - 2 п

2 ^ Et. qtqi

Разделив левую и правую части равенства на значение Е₂ и учитывая, что отношение Е 1 /Е₂ пропорционально отношению эффективных площадей рассеяния этих целей S 1 /S ₂, получим

N ₌ <71 ~ 2 ^1 NN_p 1 Qi — Qz ^1 ^2 qlql s₂^или е₂ - I 5₂-

В свою очередь, отношение N Р /E ₂ пропорционально максимальному относительному сред-

СТД% сигна лов с УМ, формируемых в ЦСC. Поэтому требование к допустимому значению можно определить в виде:

1 Qi - d -^1

I q^q^ S2

Задаваясь допустимым уменьшением A P d = 0.05...0.1 при P d = 0.8...0.9, P F = 10^-8, S 1 / S ₂ = 0.002 и I = 4, получим Q^ < (0.4...16)x10^-6 или D _a< -(48...64) дБ (рис. 2).

Основной особенностью РЛС с квазинепрерывным излучением является невозможность получения полной пространственной развязки между приемным и передающим трактами. На их входах приемных устройств таких РЛС постоянно присутствует сигнал помехи от передатчика. При этом спектр шумов мешающего сигнала передатчика после его преобразования создает помеху во всем рабочем диапазоне спектроанализатора приемного устройства.

Рассмотрим случай обнаружения малоразмерной цели, находящейся на максимальной дальности, на фоне помех, вносимых шумами сигнала передатчика. Допустимый уровень данной помехи также определим из условия допустимого снижения вероятности правильного обнаружения.

Используя уравнение радиолокации, запишем

" ^ti (4тгт?2)2    '

где: Е И - энергия сигнала за один период зондирования; G (в, е) - коэффициент усиления передающей антенны; А(β, ε) – эффективная площадь приемной антенны; β, ε – координаты цели по углу места и азимуту; S – эффективная площадь рассеивания цели; R Ц – расстояние до цели.

На вход приемного устройства попадает лишь часть энергии шумов зондирующего сигнала Е_П = Е_ИК_Р, где К_Р – коэффициент развязки между передающим и приемным трактами РЛС. Разделив обе части неравенства на Е_П, получим отношение N _Р/Е_П, определяющее допустимый уровень искажений в ЦСС с УМ. Так как в РЛС с квазинепрерывным излучением используется корреляционный метод обработки сигналов с УМ, то отношение N _Р/Е_П пропорционально максимальному относительному среднеквадратическому значению искажений ВКФ сигнала с УМ

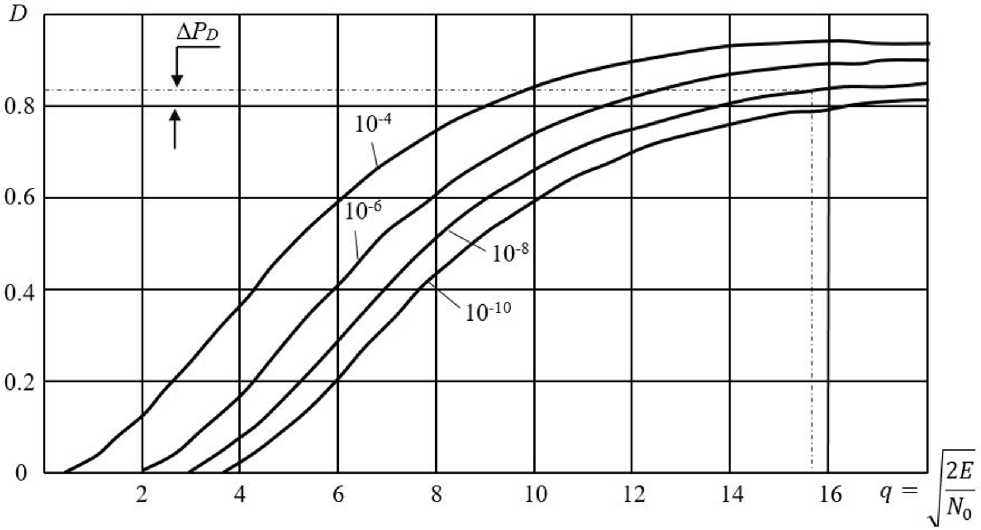
Рис. 2

Fig. 2

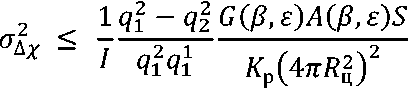
Задаваясь значениями ∆ P D = 0.05...0.1, P D = 0.8...0.9, P F = 10-8, I = 4, G (β, ε) = (3...5)×10⁴, A (β, ε) = (2...4)×10⁴ м², S = (0.8..2) м², К Р = -(80...120) дБ, R Ц = (250...400) км, получим СУ = 10^-12...10^-8 или D σ ≤ -(80...120) дБ (рис. 2).

Таким образом, в импульсных РЛС максимальное относительное среднеквадратическое значение искажений ВКФ сигнала с УМ, формируемого ЦС, не должно превышать D σ ≤ -(51...67) дБ (рис. 2). В РЛС с квазинепрерывным излучением максимальное относительное среднеквадратическое значение искажений автокорреляционной функции (АКФ) сигнала с УМ, формируемого ЦСС, не должно превышать D σ ≤ -(80...120) дБ (рис. 2).

Рекомендации по выбору количества разрядов квантования фазы, напряжения и частоты дискретизации в ЦСС

В зависимости от вида ЦСС количество источников детерминированных искажений Кии различно. При формировании сигнала с УМ в цифровых синтезаторах отсчетов фазы (ЦСОФ) и цифровых синтезаторах отсчетов напряжения (ЦСОН) с (неравномерной дискретизацией) НД осуществляется квантование фазы и его дискретизация. В ЦСОН с равномерной дискретизацией (РД) табличного типа осуществляется квантование амплитуды и дискретизация формируемого сигнала с УМ. Поэтому количество источников детерминированных искажений в этих синтезаторах равно Кии = 2. В ЦСОН с РД комбинированного типа при формировании сигнала с УМ осуществляется квантование фазы и амплитуды, а также его дискретизация, поэтому Кии = 3. При разработке ЦСС целесообразно, чтобы среднеквадратическая величина каждого источника детерминированных искажений (У- , где I = 1, 2, … Кии, была бы одинаковой. С учетом сказанного выше, используя выражение, определяющее максимальное относительное значение среднеквадратических искажений ВКФ сигналов с УМ, формируемых ЦСС с РД (R – количество отсчетов формируемого сигнала с УМ), для i-го источника детерминированных искажений можно записать

В ЦСС ширину рабочего диапазона частот, как правило, выбирают равным четверти тактовой частоты. С учетом выше сказанного относительный среднеквадратический уровень искажений, вносимых каждым источником для импульсных РЛС, составляет (У- = 4 ∙ 10^–7 … 1,6 ∙ 10^–5 при K ии = 2, и (У- = 2,6 ∙ 10^–7 … 1 ∙ 10^–5 при K _ии = 3. Для РЛС с квазинепрерывным излучением G- = 2 ∙ 10^–12 … 2 ∙ 10^–8 при K ии = 2, и G- = 1,6 ∙ 10^–12 … 1,6 ∙ 10^–3 при K ии = 3.

Количество разрядов квантования фазы для ЦСС с РД можно определить из выражения, где m – количество двоичных разрядов квантования фазы

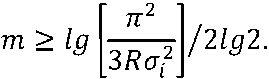
Количество разрядов квантования напряжения для ЦСС с РД можно получить из выражения, где ℓ – количество двоичных разрядов квантования напряжения

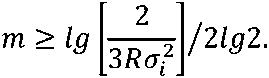
Количество разрядов компенсации временной задержки q и квантования фазы m в многоуровневых ЦСС с НД можно найти из выражения, определяющего максимальное среднеква- дратическое значение искажений ВКФ ставляя в него выражение MQ = 2m+q,

^qy_R для многоуровневых ЦСС с НД, под-

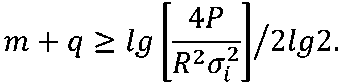
(9,а)

В двухуровневых ЦСС с НД количество разрядов компенсации временной задержки q находим из выражения, определяющего максимальное среднеквадратическое значение искаже- ний

2P/R

, в виде

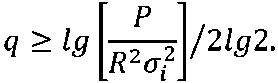
(9,б)

Выбор тактовой частоты ЦСС с РД в общем случае зависит как от ширины спектра сигнала с УМ, так и от его компактности. Численное значение тактовой частоты гот ЦСС с РД можно получить из выражения, характеризующего максимальное относительное среднеквадратическое значение искажений ВКФ, обусловленных дискретизацией, а также квантованием фазы и напряжения сигналов с УМ в ЦС с РД

и<р,Ъ1

+ ^т(^э)

^ШЭ ( △ ^<^эф/^<^э + 1)     1

Дшэф 2Г+1-1     _

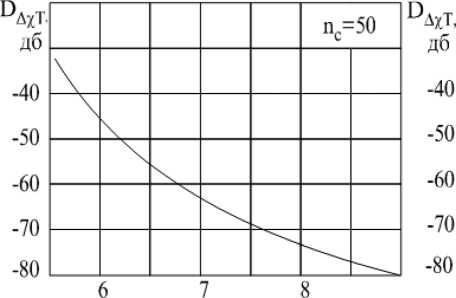
Значение тактовой частоты для линейно-частотно модулированных (ЛЧМ) сигналов, формируемых ЦСОН с РД, можно определить из графика на рис. 3.

Как следует из формул (7) … (9, б), количество разрядов квантования фазы, напряжения и компенсации временной задержки в ЦСС зависит не только от максимального относительного среднеквадратического значения искажений ВКФ , но и от количества R отсчетов сигнала с УМ. Поэтому непосредственный выбор их можно производить, задаваясь конкретным видом и параметрами сигнала с УМ.

В табл. 1 приведены расчетные данные количества разрядов квантования фазы m , напряжения ℓ и компенсации временной задержки q при использовании в импульсных РЛС и РЛС с квазинепрерывным излучением ЛЧМ сигнала с девиацией ∆ f = 5 МГц. Расчеты производились из условия, что эталонная частота ЦСС равна f э = 20 МГц, длительность ЛЧМ сигнала для импульсной РЛС Т_и = 20 мкс, а полоса пропускания спектроанализатора в РЛС с квазинепре-рывным излучением Δ f _СП = 200 Гц.

Таким образом, при предъявлении требований к суммарному уровню искажений целесообразно использовать критерий допустимого снижения вероятности правильного обнаружения по сравнению с ее потенциальным значением при фиксированной вероятности ложной тревоги. Исходя из данного критерия в импульсных РЛС максимальное относительное среднеквадратическое значение искажений ВКФ сигнала с УМ, формируемого ЦСС, не должно превы-

					nc=100

а)                                               б)

					nc=200

8          9          10                        7          8          9

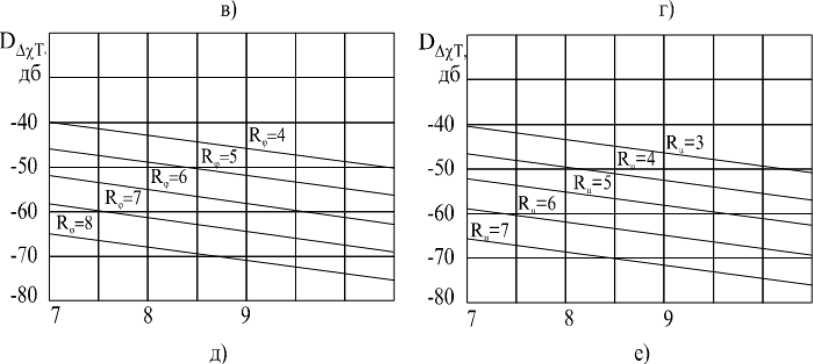
Рис. 3

Fig. 3

Таблица 1

Table 1

Вид РЛС ЦСОН ЦСОФ с РД с НД с РД с НД Импульсные РЛС (ΔΔх = -(51–67) дБ); Ти = 20 мкс; Δf = 5 МГц; fэ = 20 МГц; P/R = 0.5) m 6–9 6–8 6–8 6–8 l 5–8 – – – q – 4–7 – 4–7 РЛС с квазинепрерывным излучением (ΔΔp =-(80–120) дБ); ΔfСП = 200 МГц; Fэ = 20 МГц; P/R = 0.5) m 7–14 7–14 7–14 7–14 l 5–12 – – – q – 5–12 – 5–12 шать Dδx ≤ -(51...67) дБ. В РЛС с квазинепрерывным излучением максимальное относительное среднеквадратическое значение искажений АКФ сигнала с УМ, формируемого ЦСС, не должно превышать Dδ ≤ -(80...120) дБ.

Количество разрядов квантования фазы, напряжения и компенсации временной задержки в ЦСС зависит не только от максимального относительного среднеквадратического значения искажений ВКФ, но и от количества отсчетов сигнала с УМ. Поэтому первоначально необходимо выбрать эталонную частоту ЦСС, задаваясь видом модуляции и эффективной шириной спектра сигнала с УМ, исходя из ТТХ РЛС.