Обоснование волнового механизма разрушения замораживающих колонок при проходке вертикальных шахтных стволов

Проведя анализ статистических данных о проходках шахтных стволов в искусственно замороженных

Для характеристики нижней границы волновода, а, следовательно, для классификации его типа оценим коэффициент отражения от этой границы.

При вариации скорости продольных волн в замороженной глине в диапазоне q = Cзам = 2800 - 3200 м/с и при скорости в замороженном песке С = Сзам = 5600 м/с коэффициент преломления Р- волны составляет    C         , среднее значение n = — = 0,5 - 0,7

C2     ,     , n = 0,536, а при отношении плотностей замороженного песка рпес = 2,6 -103 кг/м3 и глины ргл = 2.0 -103 кг/м3 равно    рпес _ ^. В этом случае коэффициент

ргл

отражения по давлению определяется

V ср

( ^р пес^Спес )   ^{( р} гл^Сгл )

\ ^р пес^Спес ^{)+ ( р} гл^Сгл )

= 0,312 - 0,22

Таким образом, нижнюю границу можно отнести к разряду «сильной» границы, а данный волновод по соотношению акустических характеристик, составляющих его сред аналогичен так называемому приповерхностному каналу с верхней свободной границей (верхняя среда – воздух) и с нижней резкой границей, на которой n <  1.

При взрыве заряда ВВ на каждом из концов волновода (при этом задача решается в плоскости) внутри его возникает сложное интерференциальное волновое поле, состоящее из теоретически бесконечной суммы нормальных волн, различных номеров l . Каждая нормальная волна номера l является бегущей вдоль оси волновода (вдоль координаты Х) со своей фазовой скоростью C ,которая зависит от номера волны l , частоты источника f , высоты волновода h и свойств среды внутри волновода. В то же время каждая нормальная волна номера l является стоячей по толщине волновода h (вдоль оси Z), то есть амплитуда каждой нормальной волны номера l . Так, например, в простейшем случае, когда коэффициент отражения от нижней абсолютно жесткой границы '^ = 1, а коэффициент отражения от верхней границы раздела V = - 1 , как и в рассматриваемой задаче, потенциал Т внутри волновода определяется:

* = 2 ? £ Chb i Z 0 ■ Chb i Z ■ H$& )’    ⁽¹⁾

h I = 0 ■       1)

i i1+n         _________ bl = 1  .2J ; S = h^b2 + K2;к = — hC где Z – координата точечного источника; Z – координата точки наблюдения (рис. 2а); H(1)(SГ) Функция Ханкеля.

Известно, что каждая нормальная волна номера l распространяется вдоль слоя со скоростью: ,(2).

г »C

Cl = 7 = I

SlГ

V 12 h J где С скорость волн в среде, заполняющей волновод; X -длина волны. Причем, каждую нормальную волну номера l можно представить в виде суммы двух бегущих плоских волн с одинаковыми углами наклона O/ к границам волновода.

При увеличении номера нормальной волны l угол O; уменьшается, то есть каждая плоская волна падает на границу под большим углом. И наоборот, чем меньше номер волны l, тем более направление распространения этих плоских волн приближается к направлению оси волновода. В рассматриваемой нами модели волновода нижняя граница характеризуется конкретным значением коэффициента отражения V , который в общем случае определяется следующим образом:

mcosO - n2 - sin2 O ,(4)

V1 =              / 2. mcosO + nn - sin O где    C    p    угол падения волны на границу.

n = —;m =

C1

Аналогичное выражение можно записать и для коэффициента отражения от второй границы V .

При наличии у волновода двух границ с произ вольными коэффициентами отражения V и V после нормальных волн внутри волновода определяется в общем виде следующим образом:

T= n K ^

( e ^{- bZ} •

+ V 1 e^bZ )( e - ^bZ + V 1 e^bZ )

V 1 Th* ' 2 ^h )

H ₀ ^{( 1 )}( KrSin O _l ) Sin O _l

,    (5)

где b = ik cos O ; 6 - корни дисперсионного уравнения

1 - V 1 ( O ) ■ V ₂ ( O ) e ² i^{kh cos O} = 0 ,    (6)

В случае, когда верхняя граница абсолютно мягкая ('2 = -1), на достаточно больших расстояниях от источника (r > 1), при которых можно воспользо-X ваться асимптотическим представлением функции Ханкеля в (5) выражение для нормальных волн в таком волноводе имеет вид [2]:

^ =

у 2 п НЕ. Д ^h ^Г

^Xl sin

X, 1 1 - ^Z !■ sin X ,11 —⁰ I

¹ 1 h J L ¹ 1 h J.

sin ² X l tgX l

Xl - sin Xi cos Xi------- m2

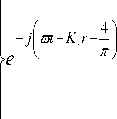
,(7)

где Z , Z - координаты расположения соответственно излу- чателя и приемника волн.

Xi = khcos O ; Ki = k sin O k /1 -|     |,     ⁽⁸⁾

^{l                            l} V I kb J

Считается, что поле внутри волновода создается точечным (сферическим) источником:

jkR

^ 0 = A 0— ; R = V( z - z 0 ) ² + r ² ,     ⁽⁹⁾

R где A – амплитуда колебаний источника

Qq - его объемная скорость, Q q = VS

S – площадь излучающей поверхности,

V – колебательная скорость на сфере .

В дальнейших расчетах амплитуда первичного поля принимается за единичную ( A = 1) .

Величина X является корнем дисперсионного урав- нения:   ctgX = ^XX2 -(Khv)2 ,  (10)

mX где v2 = 1 - n2 : iX = bh; K = —, (11)

C

Каждая нормальная волна номера l характеризуется своим распределением амплитуды по толщине волновода и своей фазовой скоростью C и коэффици- ентом поглощения в :

KhC      „_ImV ( Kh ) ² - X i , (12)

^Ci =                  ; ^e i =

R i V( Kh ) ² - X_t             ^h

Для оценки особенностей распространения нормальных волн, создаваемых взрывным источником в волноводе между свободной поверхностью забоя ствола и горизонтальной границей раздела нами были проведены расчеты распределения амплитуд первых трех нормальных волн ( l= 1,2,3) по высоте волновода ( A = f ( Z ) ) для волноводов с различной мощностью h .

При проведении таких расчетов рассматривались средние значения характеристик волноводов C = C Зам = 3000 м/с;            С ₂ = С За* = 5600

гл                                      пес м/с; f = 4000    Гц; r = 6 м.    В    этом    случае

n = 0,536; v = 0,844; K = 8,37 • 10-1; 2 = 0,75.

Величина корня дисперсионного уравнения для нормальных волн номеров l= 1,2,3 определялась на основании графического изображения его решения по соответствующей кривой. Расчеты проводились для волноводов со следующей высотой h : 0,5;0,75;1;2;3;4.

при данных расчетах принималось, что координата источника Z соответствует центру каждого слоя.

Значения характеристик для каждого волновода и соответствующих нормальных волн приведены в табл. 1.

Таблица 1

Характеристики волновода и нормальных волн различных номеров l

h , м	h 2	Kh v	l	X 1	K l ,м -1	Z 0 ,м
0.5	0,67	3,532	1	2,05	5,978	0,25
			2
0,75	1	7.064	1	2,3	7,788	0.375
			2	4.72	5,518
1,0	1,33	7,064	1	2.5	7,988	0,5
			2	5,1	6,637
			3	-	-
2,0	2.66	14.13	1	3,1	8,225	1
			2	5,4	7,92
			3	8,9	7,26
3.0	4	21,19	1	2,9	8.314	1.5
			2	5.8	8,144
			3	8,4	7.89
4.0	5,33	28,26	1	5,4	8,26	2
			2	5,9	8,24
			3	8.5	8,096

^ 051(z)

0.8

0.6

0.4

0.2

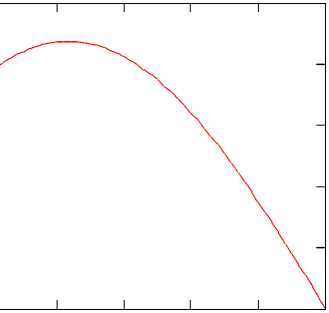
0           0.1          0.2          0.3          0.4          0.

z

Рис.2. Распределение амплитуды первой нормальной волны по высоте волновода ( h = 0,5 м , Z 0 = 0,25 м ).

Для оценки возможности возбуждения каждой модой толщинного резонанса в вертикальном слое с неоднородной границей рассчитывались углы @ i :

Расчеты проводились в среде Mathcad методом ранжированных переменных.

Результаты расчетов представлены на (рис. 2-7).

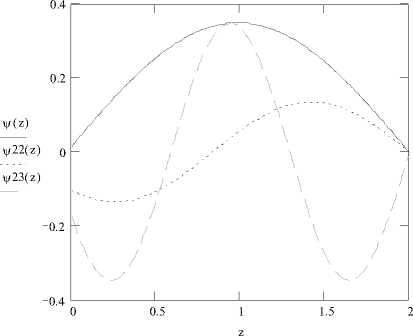
Рис. 4. Распределение амплитуды первых трех нормальных ^волн по высоте волновода ( h = 2 м ; Z 0 = 1 м );1 - 1 = 1;2 - 1 = 2;3 - 1 = 3

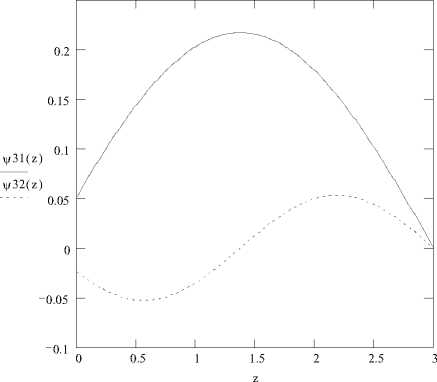
Рис. 5. Распределение амплитуды первых двух нормальных волн по высоте волновода (h = 3м; Z0 = 1,5м);1 - 1 = 1;2 - 1 = 2

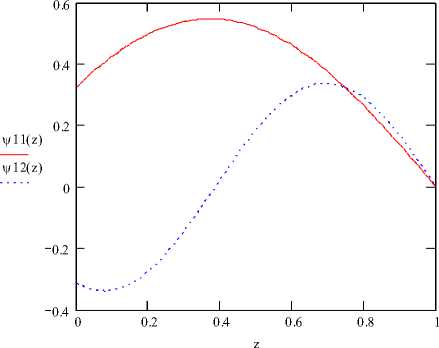
Рис. 3. Распределение амплитуды первых двух нормальных волн по высоте волновода (h = 1 м; z0 = 0,5*)д -1 = 1;2 -1 = 2

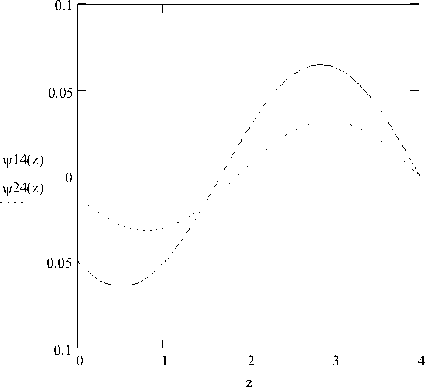
Рис. 6. Распределение амплитуды первых двух нормальных волн по высоте волновода ( h = 4 м ; Z _o = 2 м ) 1 - l = 1;2 - 1 = 2 .

Из полученных распределений A = f ( Z ) видно, что наибольшая в сечении волновода амплитуда наблюдается во всех случаях у основной ( l = 1 ) нормальной волны.. Величина угла А представлена в табл. 2.

Таблица 2

Угол А в зависимости от h распределения амплитуды основной моды по сечению волновода – оно становится двугорбым. На основании этого можно сделать вывод о том, что при изменении расстояния от забоя ствола до вертикальной границы раздела в диапазоне от 0,5 до 3 м наблюдается ярко выраженная канализация волновой энергии источника внутри волновода и лишь при расстоянии h > 4 м этот волновой эффект практически незаметен.

На основании проведенных исследований можно предложить следующие практические рекомендации по совершенствованию технологии проходки ствола в условиях применения способа искусственного замораживания. так при применении буровзрывных работ во время проходки ствола в случае наличия впереди забоя ствола горизонтальной границы раздела между замороженными породами, с целью исключения возможного разрушения замораживающих колонок рекомендуется использование БВР при расстоянии от забоя до горизонтальной границы не менее 4-рех метров. При этом с целью увеличения вероятности безаварийной ситуации при проведении буровзрывных работ на этих глубинах рекомендуется размещение зарядов ВВ на глубину до 0,5 м от плоскости забоя. При проходке на расстоянии менее 4-х м от границы раздела необходимо использовать другие способа проходки в замороженных породах, такие как создание разгрузочной щели с помощью компенсационных шпуров.

l 1 / h 1 м	0,5		0,75	1,0	2,0	3,0	4,0
1	A l	60,72	68,53	72,60	79,34	83,39	80,73
2		-	41,32	52,48	71,22	76,64	79,86
3		-	-		57,86	70,49	75,2

В связи с этим в дальнейшем будем анализировать поведение только двух первых мод ( l = 1 и 2) при изменении высоты волновода. Значения максимальной амплитуды первых двух мод для волновода с различной высотой h представлено в табл. 3.

Таблица 3

Зависимость максимальной амплитуды A от высоты волновода

l / h	A l условные единицы
	-0,5	0,75	1,0	2,0	3,0	4,0
1	0,877	0,653	0,553	0,356	0,219	0,066
2	-	-	0,344	0,139	0,055	0,033
A 1 ( 2 ) М ( h i )	0,712	0,545	0,644	1	1,625	5,394

Из табл. 3 видно, что чем меньше высота волновода h , тем больше максимальная амплитуда основной моды. При увеличении высоты волновода вплоть до h = 3 , амплитуда A ( h ) незначительно уменьшается. И только для волновода с h = 4 наблюдается резкое уменьшение амплитуды. Так, отношение амплитуды A i для волновода с h = 2 м к той же амплитуде для волновода с h = 4 м составляет более 5 раз. Кроме того, у волновода с h = 4 изменяется характер